函数优化是研究函数输入以获得函数最大或最小输出的学科。
优化算法种类繁多,在简单易于可视化的测试函数上研究和开发优化算法的直觉非常重要。
一维函数接收单个输入值并输出输入的单个评估。它们可能是研究函数优化时最简单的测试函数类型。
一维函数的优点在于,它们可以被可视化为二维图,其中函数的输入位于 x 轴,函数的输出位于 y 轴。函数的已知最优值以及任何函数采样也可以绘制在同一张图上。
在本教程中,您将发现标准的一维函数,您可以在研究函数优化时使用它们。
通过我新书《机器学习优化》开启您的项目,书中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
函数优化的单变量(1D)测试函数
照片作者 Max Benidze,保留部分权利。
教程概述
我们可以使用许多不同类型的一维测试函数。
尽管如此,函数优化领域中存在常用的标准测试函数。此外,我们在测试不同算法时可能希望选择测试函数的特定属性。
在本教程中,我们将探讨少量简单的一维测试函数,并按其属性将它们分为五组;它们是:
- 凸单峰函数
- 非凸单峰函数
- 多峰函数
- 不连续函数(非光滑)
- 有噪声的函数
每个函数都将通过 Python 代码呈现,其中包含目标目标函数的实现以及函数采样,该采样显示为带有清晰标记的函数最优值的折线图。
所有函数都呈现为最小化问题,例如找到导致函数最小(最小)输出的输入。任何最大化函数都可以通过对所有输出添加负号来变成最小化函数。类似地,任何最小化函数都可以通过相同的方式变成最大化函数。
我没有发明这些函数;它们取自文献。有关参考,请参见“进一步阅读”部分。
然后,您可以选择并复制一个或多个函数的代码,在您自己的项目中研究或比较优化算法的行为。
凸单峰函数
凸函数是指domain中的任意两点之间的连线都保持在domain内的函数。
对于显示为二维图的一维函数,这意味着该函数具有碗状,并且两点之间的连线保持在碗的上方。
单峰意味着函数只有一个最优值。凸函数可能单峰,也可能不是;类似地,单峰函数可能凸,也可能不是。
下面函数的取值范围限制在 -5.0 到 5.0 之间,最优输入值为 0.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 凸单峰优化函数 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 0.0 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个函数的折线图,并用红线标记最优值。
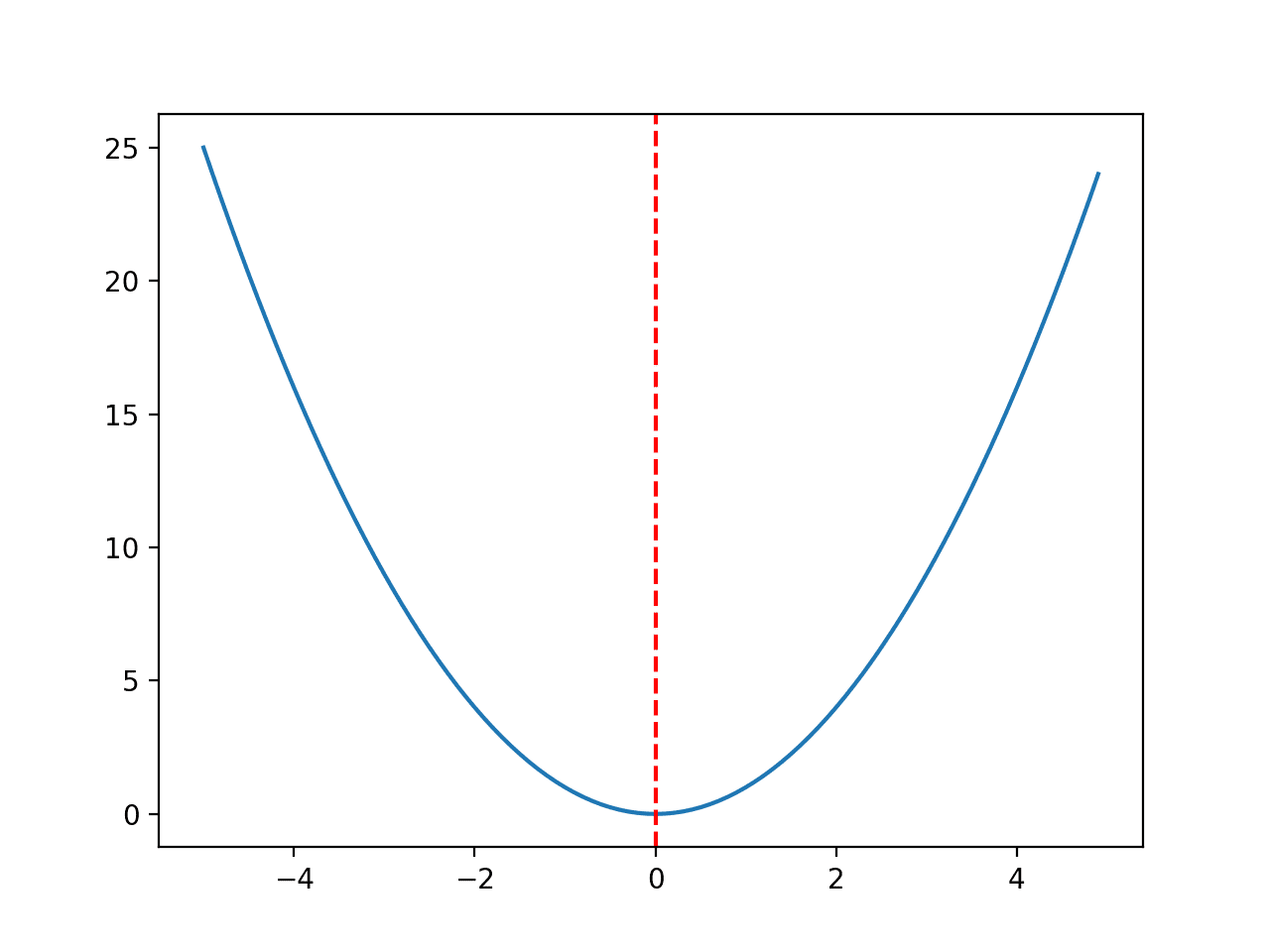
凸单峰优化函数折线图
通过加减常数,例如 5 + x^2,可以使该函数在数轴上向前或向后移动。
如果希望将最优输入值移离 0.0,这将非常有用。
非凸单峰函数
如果domain中的某个连线不能保持在domain内,则该函数是非凸函数。
这意味着可能找到domain中的两个点,它们之间的连线与函数图交叉。
通常,如果一维函数的图有多个波峰或波谷,我们就能立即知道该函数是非凸的。尽管如此,非凸函数可能单峰,也可能不是。
我们感兴趣的大多数实际函数都是非凸函数。
下面函数的取值范围限制在 -10.0 到 10.0 之间,最优输入值为 0.67956。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 非凸单峰优化函数 from numpy import arange from numpy import sin from numpy import exp from matplotlib import pyplot # 目标函数 def objective(x): return -(x + sin(x)) * exp(-x**2.0) # 定义输入范围 r_min, r_max = -10.0, 10.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 0.67956 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个函数的折线图,并用红线标记最优值。
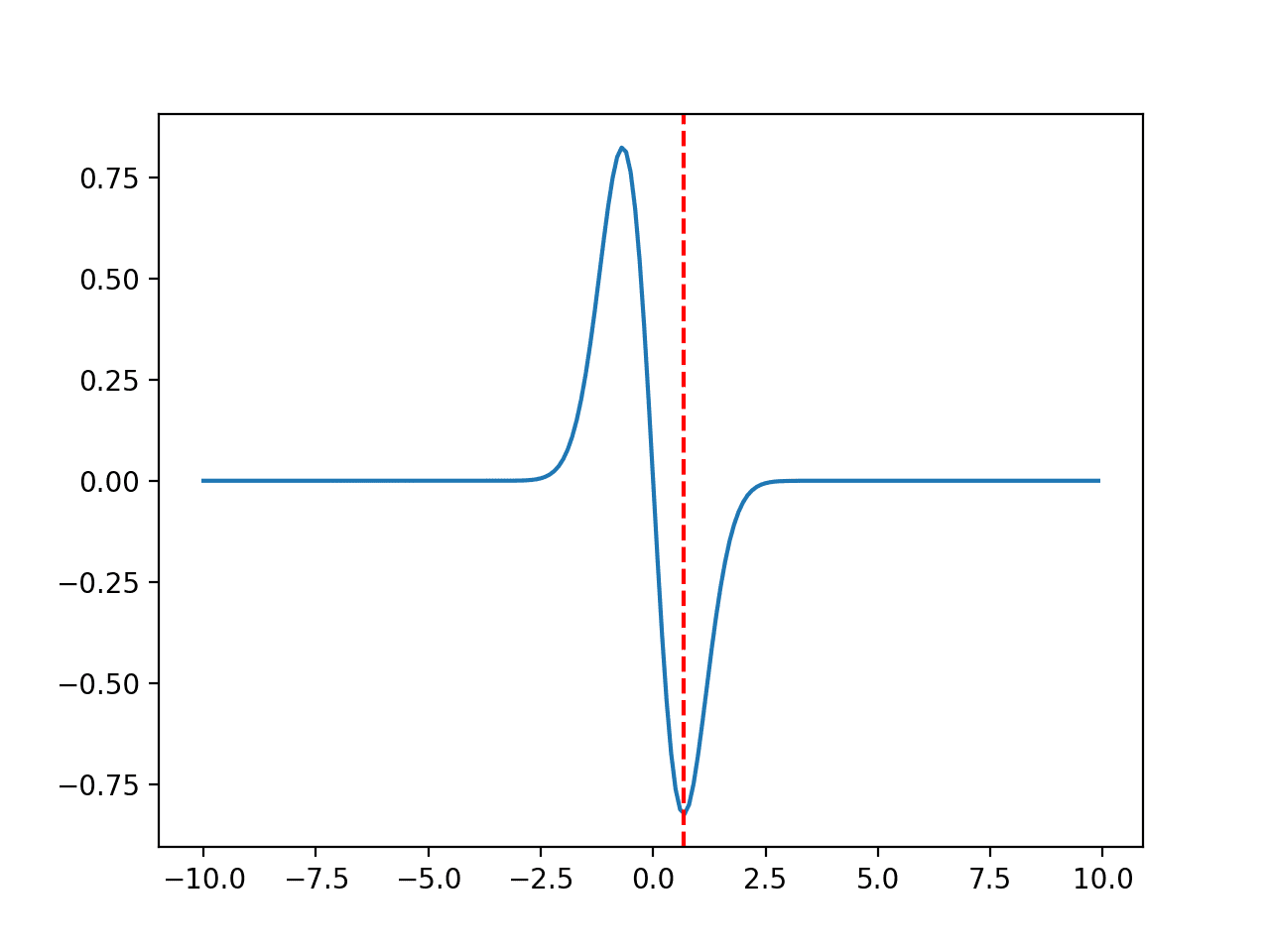
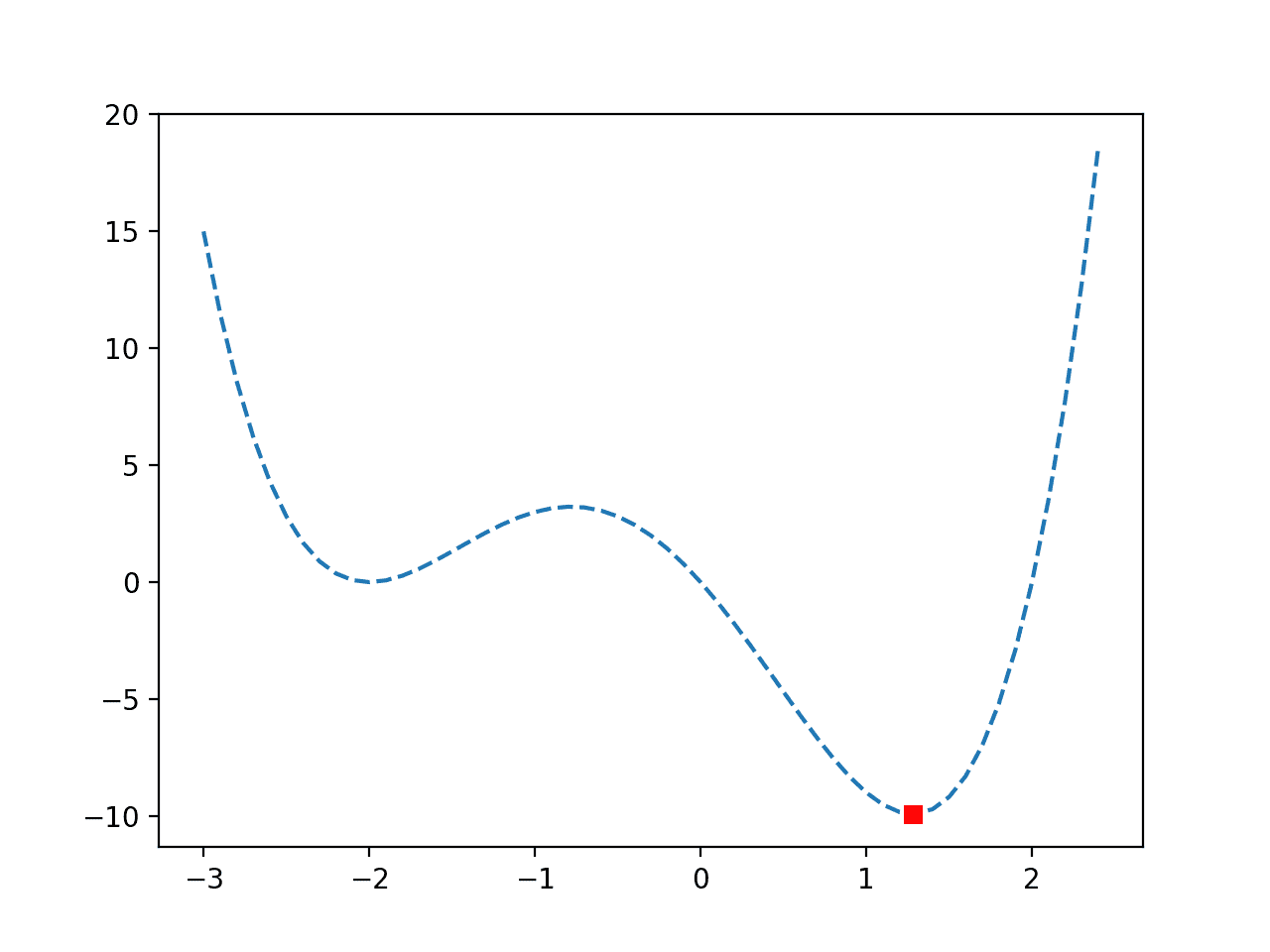
非凸单峰优化函数折线图
多峰函数
多峰函数是指具有一个以上“峰”或最优值(例如谷)的函数。
多峰函数是非凸的。
可能存在一个全局最优值和一个或多个局部或误导性的最优值。或者,可能存在多个全局最优值,即导致函数最小输出的多个不同输入。
让我们来看几个多峰函数的例子。
多峰函数 1
范围限制在 -2.7 到 7.5 之间,最优输入值为 5.145735。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 多峰函数 from numpy import sin from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return sin(x) + sin((10.0 / 3.0) * x) # 定义输入范围 r_min, r_max = -2.7, 7.5 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 5.145735 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个函数的折线图,并用红线标记最优值。
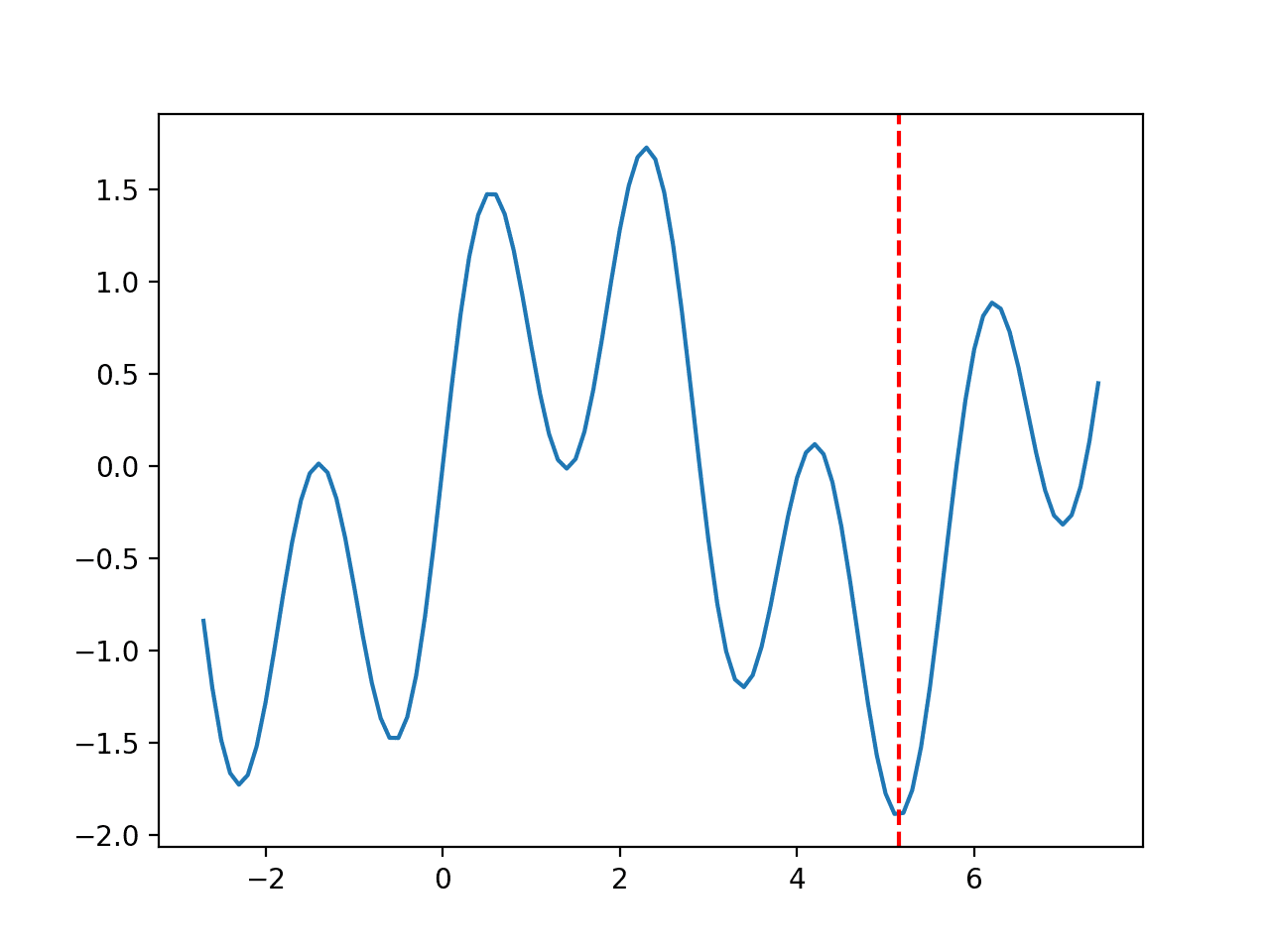
多峰函数 1 折线图
多峰函数 2
范围限制在 0.0 到 1.2 之间,最优输入值为 0.96609。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 多峰函数 from numpy import sin from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return -(1.4 - 3.0 * x) * sin(18.0 * x) # 定义输入范围 r_min, r_max = 0.0, 1.2 # 以 0.01 的增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.01) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 0.96609 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个函数的折线图,并用红线标记最优值。
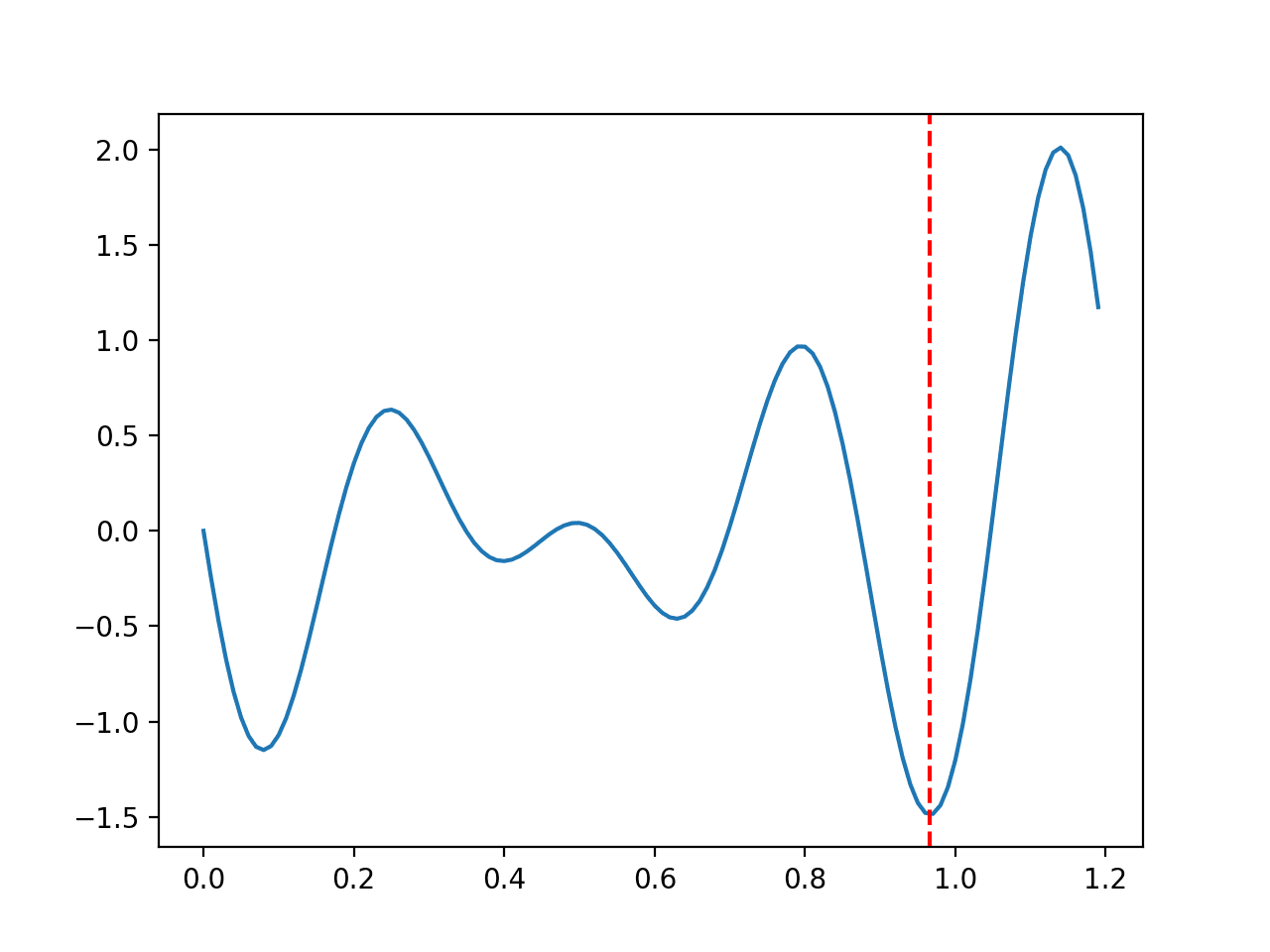
多峰函数 2 折线图
多峰函数 3
范围限制在 0.0 到 10.0 之间,最优输入值为 7.9787。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 多峰函数 from numpy import sin from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return -x * sin(x) # 定义输入范围 r_min, r_max = 0.0, 10.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 7.9787 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个函数的折线图,并用红线标记最优值。
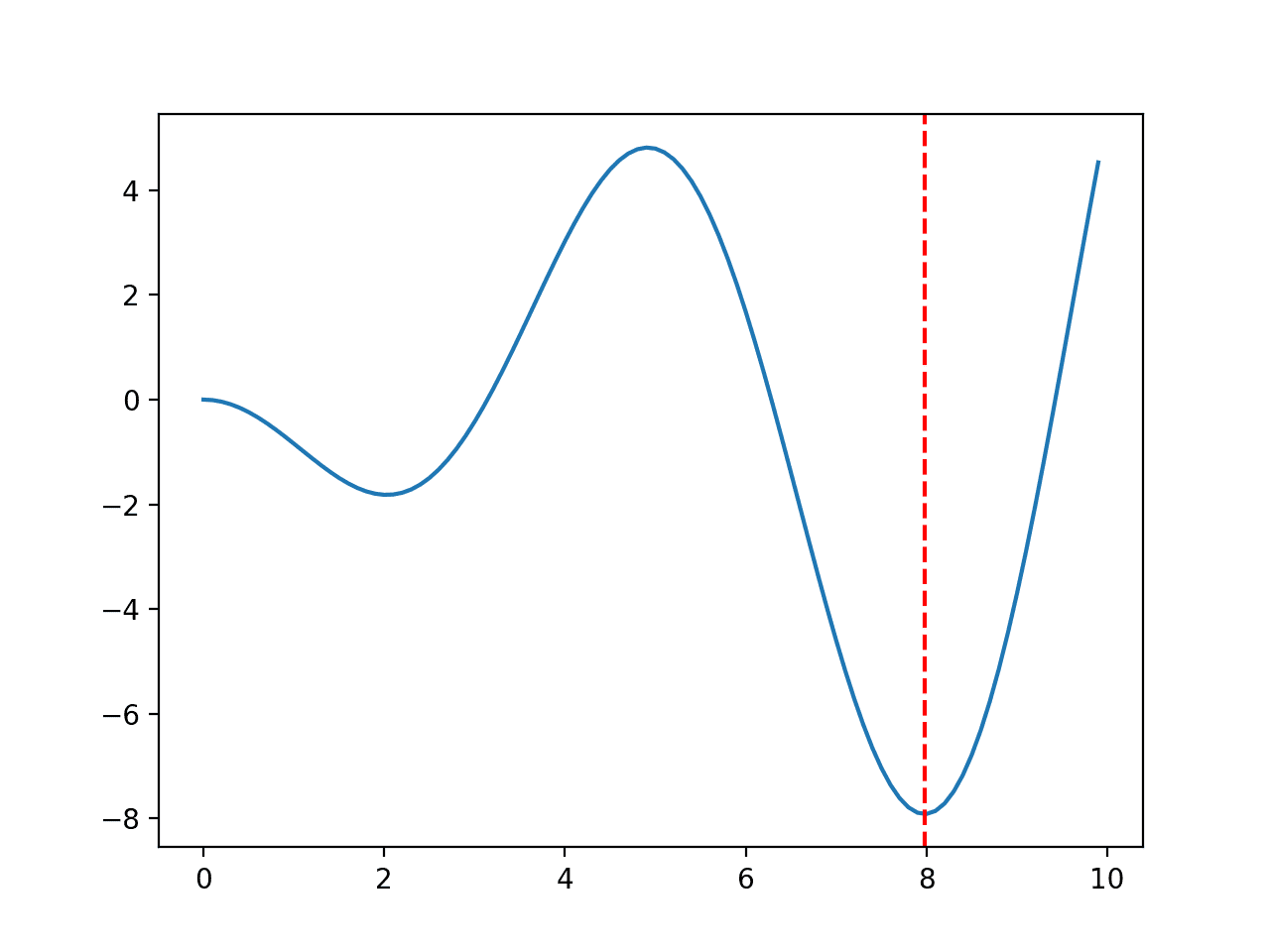
多峰函数 3 折线图
不连续函数(非光滑)
函数可能存在不连续性,这意味着函数的输入平滑变化可能导致输出非平滑变化。
我们可以称具有此属性的函数为非光滑函数或不连续函数。
存在多种类型的不连续性,但一个常见的例子是函数输出值中的跳跃或急剧方向变化,这在函数图上很容易看到。
不连续函数
范围限制在 -2.0 到 2.0 之间,最优输入值为 1.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 非光滑优化函数 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): if x > 1.0: return x**2.0 elif x == 1.0: return 0.0 return 2.0 - x # 定义输入范围 r_min, r_max = -2.0, 2.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = [objective(x) for x in inputs] # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 1.0 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
运行示例会创建一个函数的折线图,并用红线标记最优值。
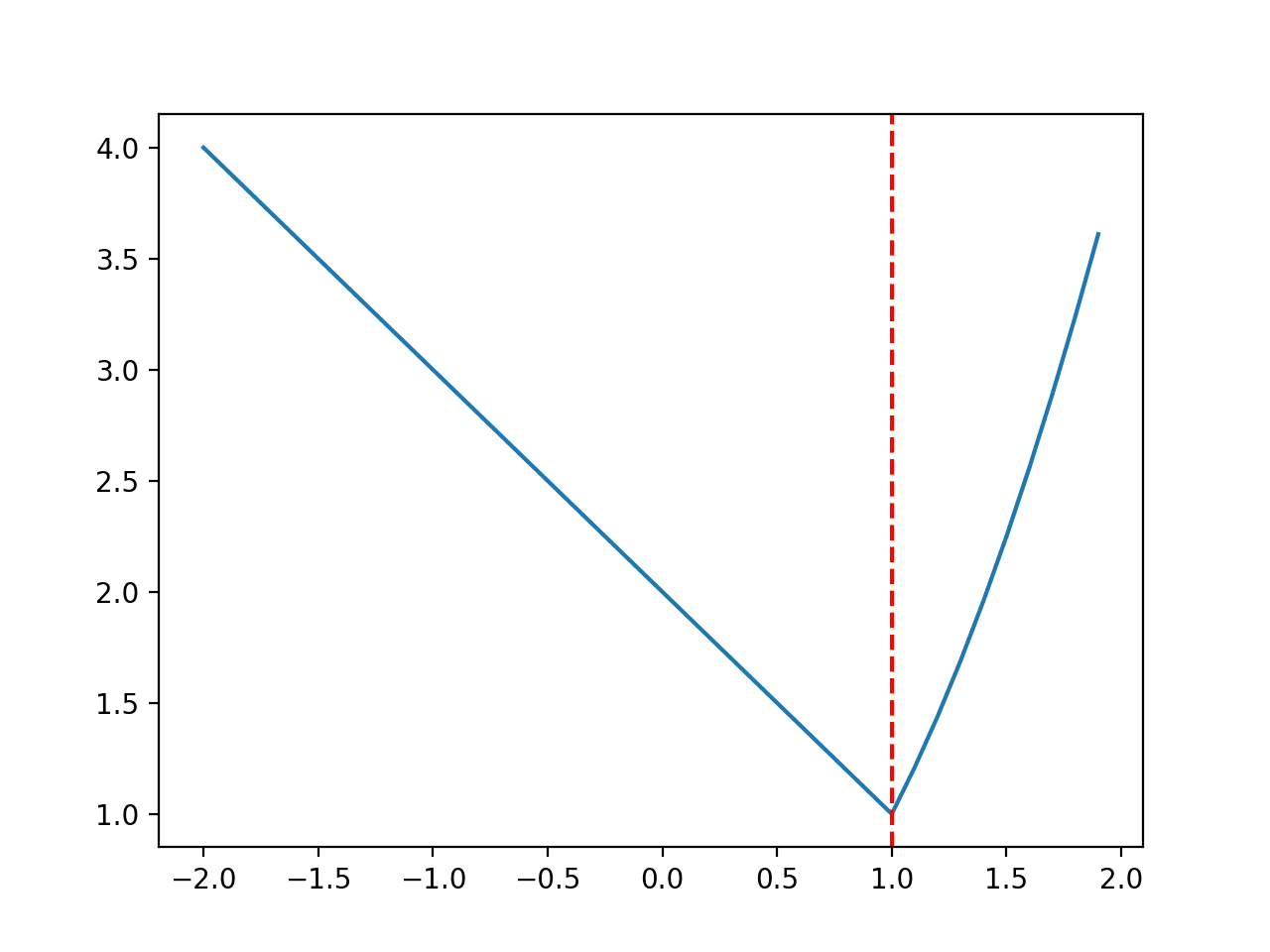
不连续优化函数折线图
有噪声的函数
函数可能存在噪声,这意味着每次评估都可能包含一个随机分量,每次都会轻微改变函数的输出。
任何无噪声函数都可以通过向输入值添加小的正态随机数来使其产生噪声。
下面函数的取值范围限制在 -5.0 到 5.0 之间,最优输入值为 0.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 有噪声的优化函数 from numpy import arange from numpy.random import randn from matplotlib import pyplot # 目标函数 def objective(x): return (x + randn(len(x))*0.3)**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 定义最优输入值 x_optima = 0.0 # 在最优输入处画一条竖线 pyplot.axvline(x=x_optima, ls='--', color='red') # 显示绘图 pyplot.show() |
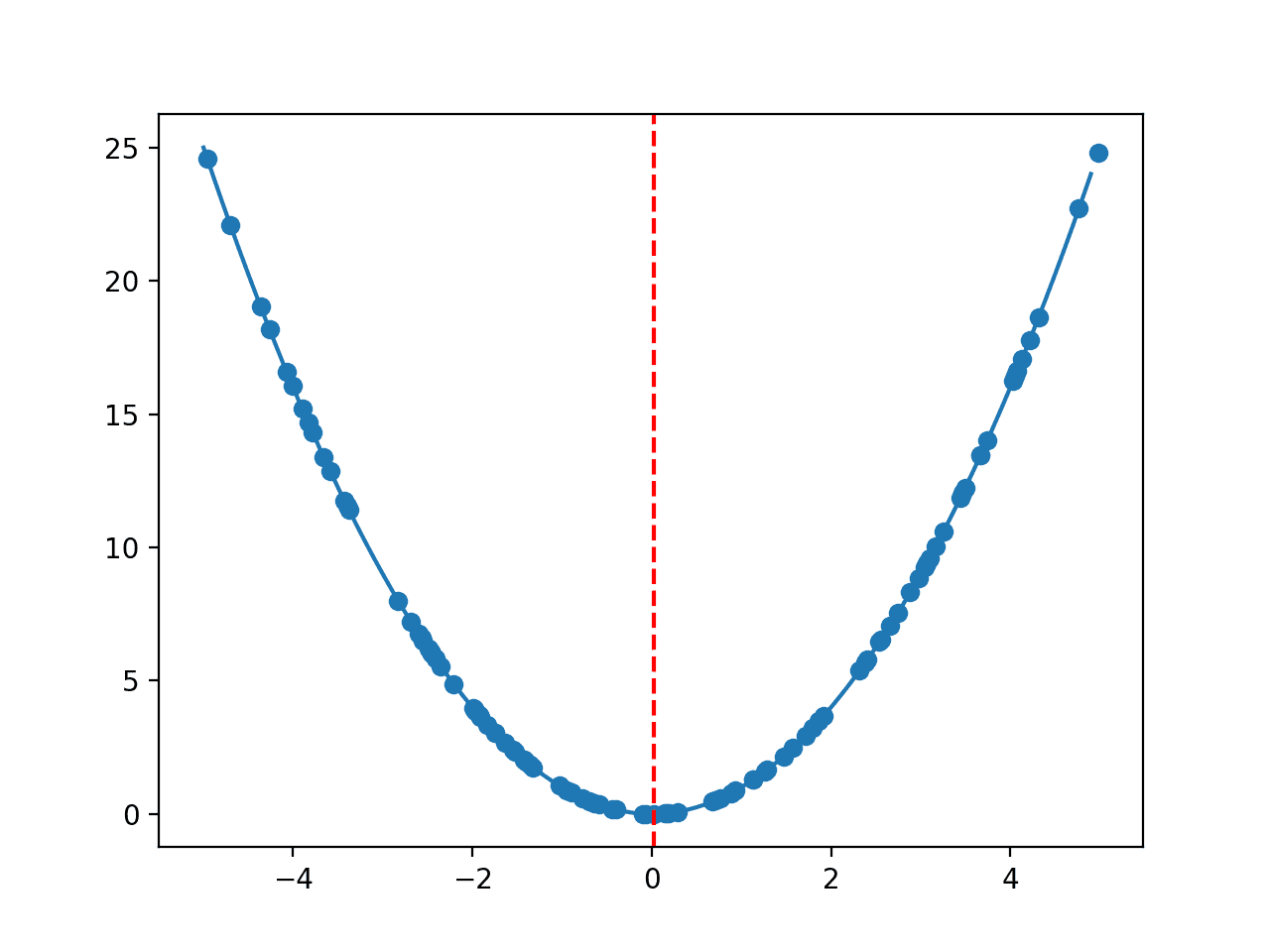
运行示例会创建一个函数的折线图,并用红线标记最优值。
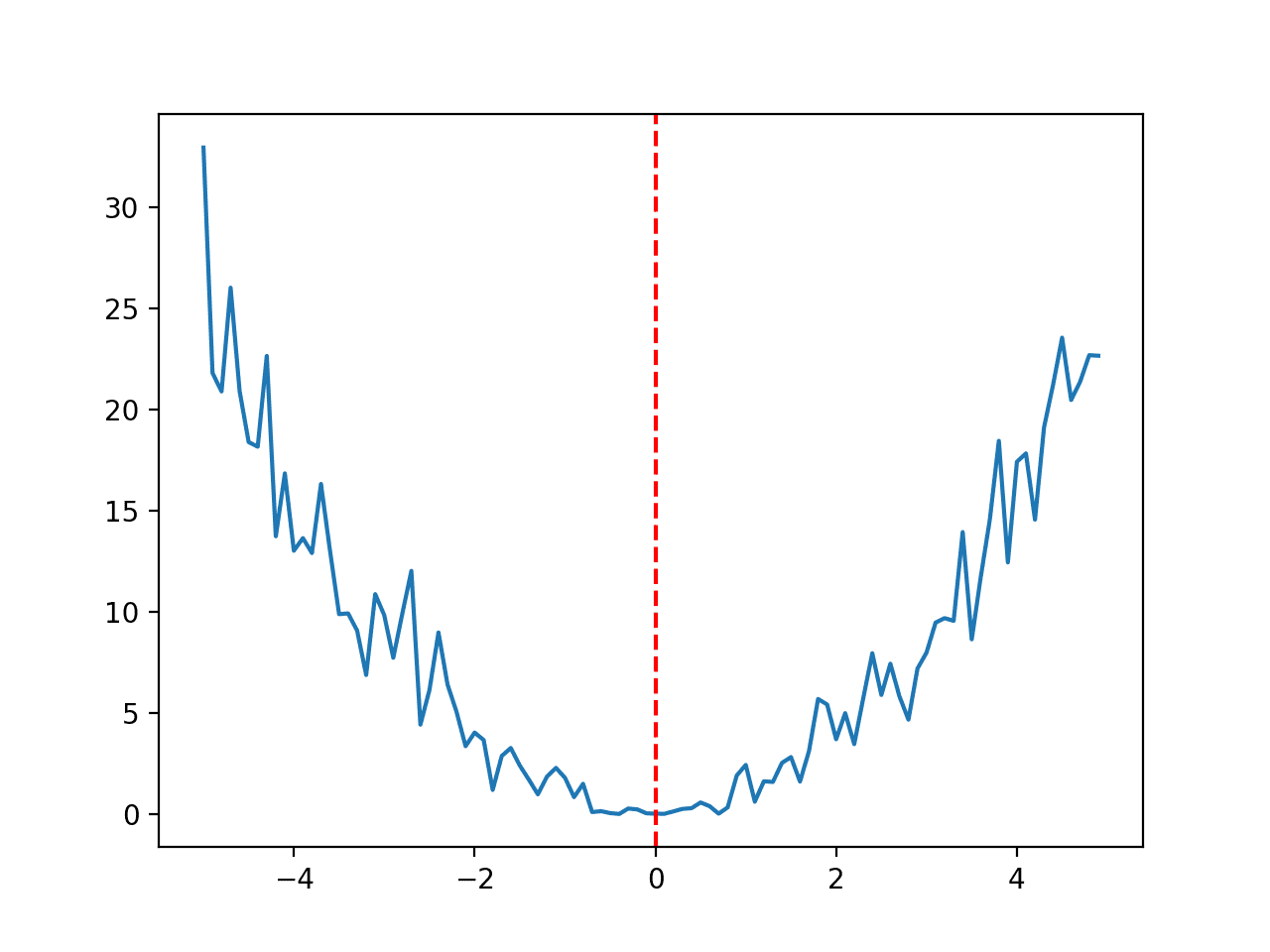
有噪声的优化函数折线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
总结
在本教程中,您了解了可用于研究函数优化的一维标准函数。
您是否使用了以上任何函数?
请在下面的评论中告诉我您使用了哪个。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



嗨,Jason,
我是一名常读这篇文章的读者,一直很欣赏您帖子中非常务实的精神和启发。但在此点上,连续性的数学不精确性让我有些困扰。
该示例实际上在除拐点以外的所有地方都是连续且可微的,其中左导数和右导数仅相差一个常数。因此,牛顿法和其他优化方法通常仍然非常稳健。
我认为我们机器学习的损失函数通常是连续的并且相当光滑,平方误差就是为此。但由于正则化约束,有时它们不是连续可微的,问题仅出现在一个很小的集合(零测度)上,而这在实践中我们永远不会遇到,或者当它发生时,我们可以将其噪声化。
如果这听起来像挑剔,我很抱歉,但我认为读者会从这里开始研究并对这个细节感到非常困惑,因为我记得很久以前我自己的困惑 😀
祝好,再次感谢您提供所有这些资源🙂
谢谢分享。