函数优化是一个研究领域,它寻求函数的输入,以获得函数的最大值或最小值。
有大量的优化算法,重要的是在简单易于可视化的测试函数上研究和开发优化算法的直觉。
二维函数需要两个输入值(x和y)并输出输入的单个评估值。它们是研究函数优化时最简单的测试函数类型之一。二维函数的优点在于它们可以可视化为等高线图或曲面图,显示了问题域的地形,并用点标记了最优值和域的样本。
在本教程中,您将发现标准二维函数,您可以在研究函数优化时使用它们。
用我新书《机器学习优化》为您的项目奠定基础,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
函数优化的二维(2D)测试函数
图片由DomWphoto拍摄,保留部分权利。
教程概述
二维函数是接受两个输入变量并计算目标值的函数。
我们可以将两个输入变量视为图形上的两个轴,x和y。函数的每个输入是图形上的一个点,函数的结果可以看作是图形上的高度。
这使得函数可以被概念化为一个曲面,我们可以根据曲面的结构来表征函数。例如,对于导致目标函数相对输出值较大的输入点,可以认为是山丘;对于导致目标函数相对输出值较小的输入点,可以认为是山谷。
一个曲面可能有一个主要的特征或全局最优值,也可能有很多特征,优化过程很容易卡住。曲面可以是平滑的、有噪声的、凸的,以及我们在测试优化算法时可能关心的各种其他属性。
我们可以使用许多不同类型的简单二维测试函数。
然而,在函数优化领域,有一些标准的测试函数被广泛使用。我们也可以根据测试算法时希望选择的测试函数特性来选择。
我们将在本教程中探讨一些简单的二维测试函数,并按其特性进行分组,分为两类;它们是
- 单峰函数
- 单峰函数 1
- 单峰函数 2
- 单峰函数 3
- 多峰函数
- 多峰函数 1
- 多峰函数 2
- 多峰函数 3
每个函数将通过Python代码呈现,包含目标函数的实现以及通过曲面图显示的函数采样。
所有函数都表示为最小化函数,即找到导致函数最小(最小)输出的输入。任何最大化函数都可以通过在其所有输出上加一个负号来变成最小化函数。同样,任何最小化函数也可以以相同的方式变成最大化函数。
这些函数并非我所发明;它们取自文献。有关参考,请参阅进阶阅读部分。
然后,您可以选择并复制粘贴代码中的一个或多个函数,以在您自己的项目中研究或比较优化算法的行为。
单峰函数
单峰意味着函数只有一个全局最优值。
一个单峰函数可能包含或不包含凸函数。凸函数是指在线段连接域中的任意两点时,该线段始终保持在域内的函数。对于表示为等高线图或曲面图的二维函数,这意味着函数具有碗状,并且连接两点的线段保持在碗的上方或内部。
让我们看几个单峰函数的例子。
单峰函数 1
范围被限制在-5.0到5.0之间,全局最优值为[0.0, 0.0]。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 单峰测试函数 from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建一个函数曲面图。
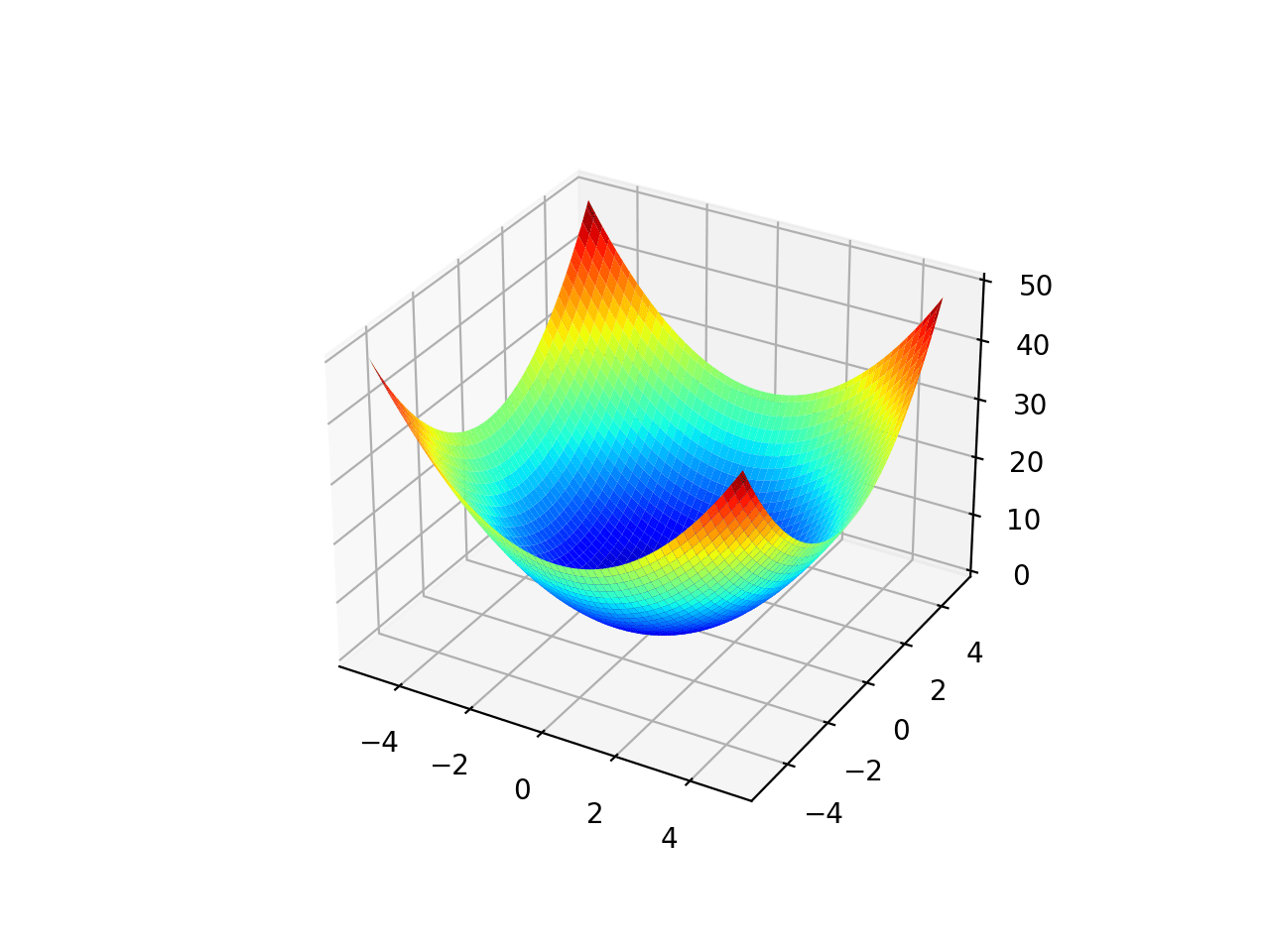
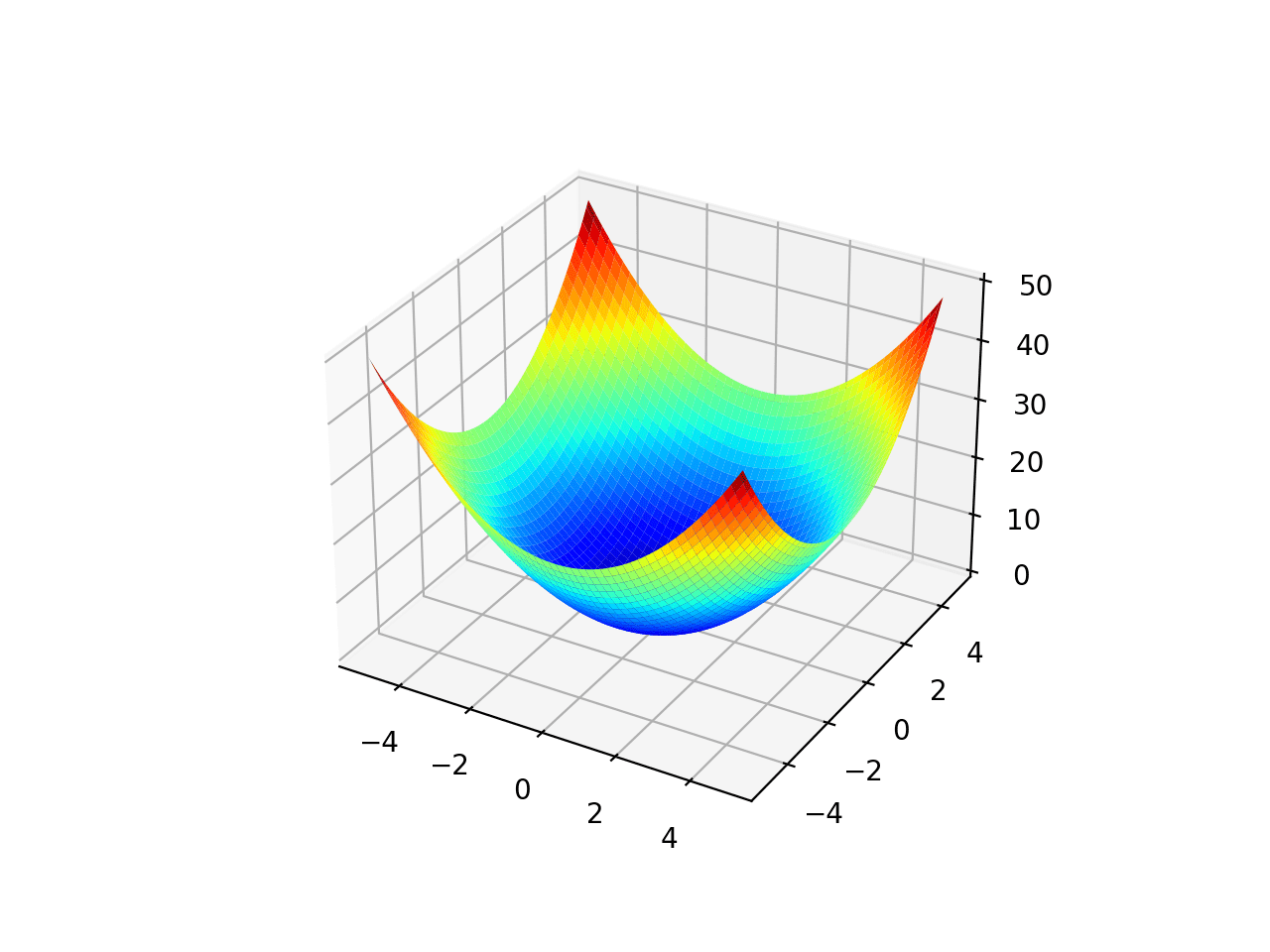
单峰优化函数 1 的曲面图
单峰函数 2
范围被限制在-10.0到10.0之间,全局最优值为[0.0, 0.0]。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 单峰测试函数 from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return 0.26 * (x**2 + y**2) - 0.48 * x * y # 定义输入范围 r_min, r_max = -10.0, 10.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建一个函数曲面图。
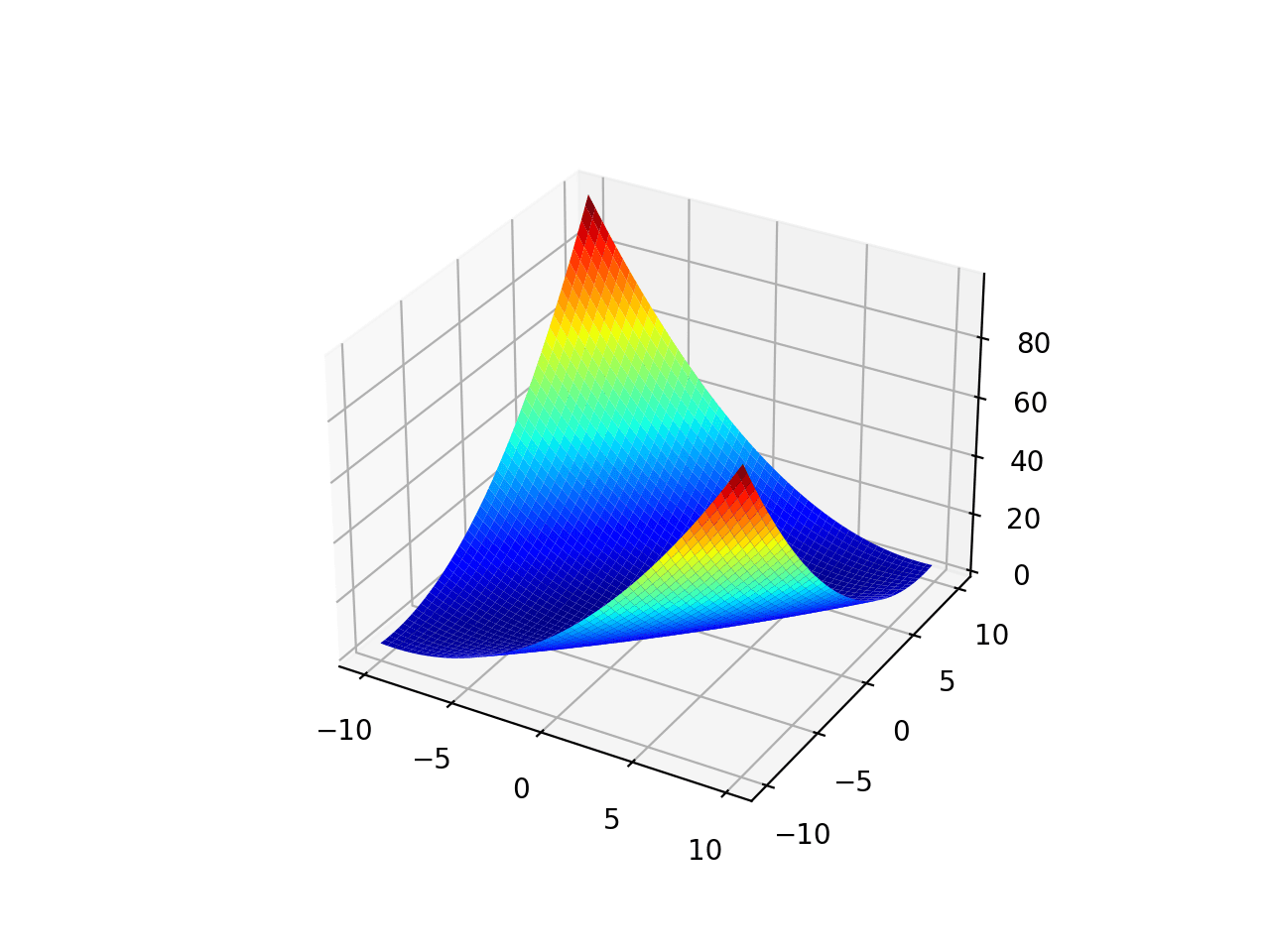
单峰优化函数 2 的曲面图
单峰函数 3
范围被限制在-10.0到10.0之间,全局最优值为[pi, pi]。该函数称为 Easom 函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# 单峰测试函数 from numpy import cos from numpy import exp from numpy import pi from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return -cos(x) * cos(y) * exp(-((x - pi)**2 + (y - pi)**2)) # 定义输入范围 r_min, r_max = -10, 10 # 以0.01的增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.01) yaxis = arange(r_min, r_max, 0.01) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建一个函数曲面图。
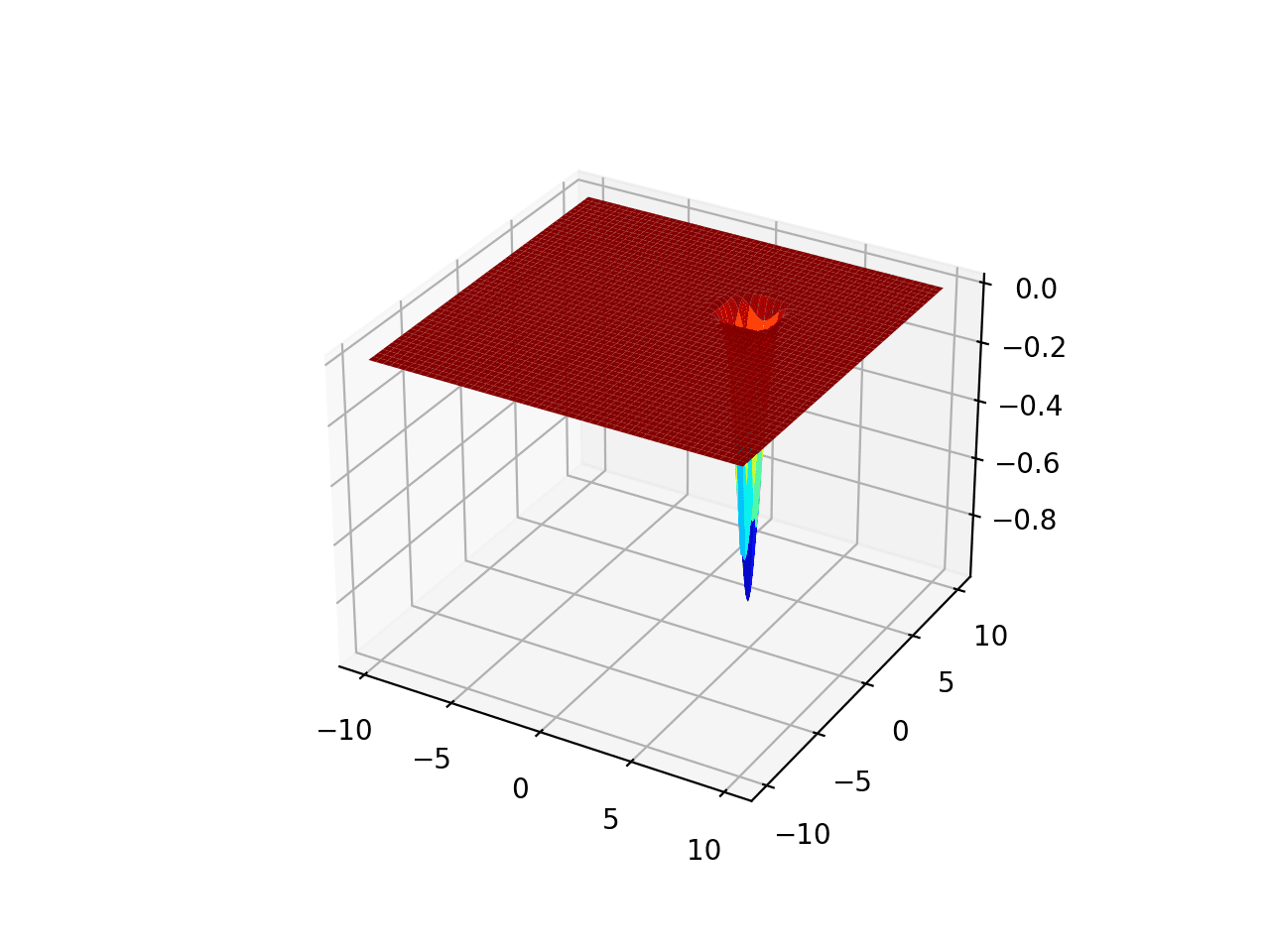
单峰优化函数 3 的曲面图
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
多峰函数
一个多峰函数是指一个具有多个“峰”或最优值(例如,谷)的函数。
多峰函数是非凸的。
可能有一个全局最优值和一个或多个局部或欺骗性的最优值。或者,可能存在多个全局最优值,即多个不同的输入产生相同的函数最小输出。
让我们看几个多峰函数的例子。
多峰函数 1
范围被限制在-5.0到5.0之间,全局最优值为[0.0, 0.0]。该函数称为Ackley 函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 多峰测试函数 from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建一个函数曲面图。
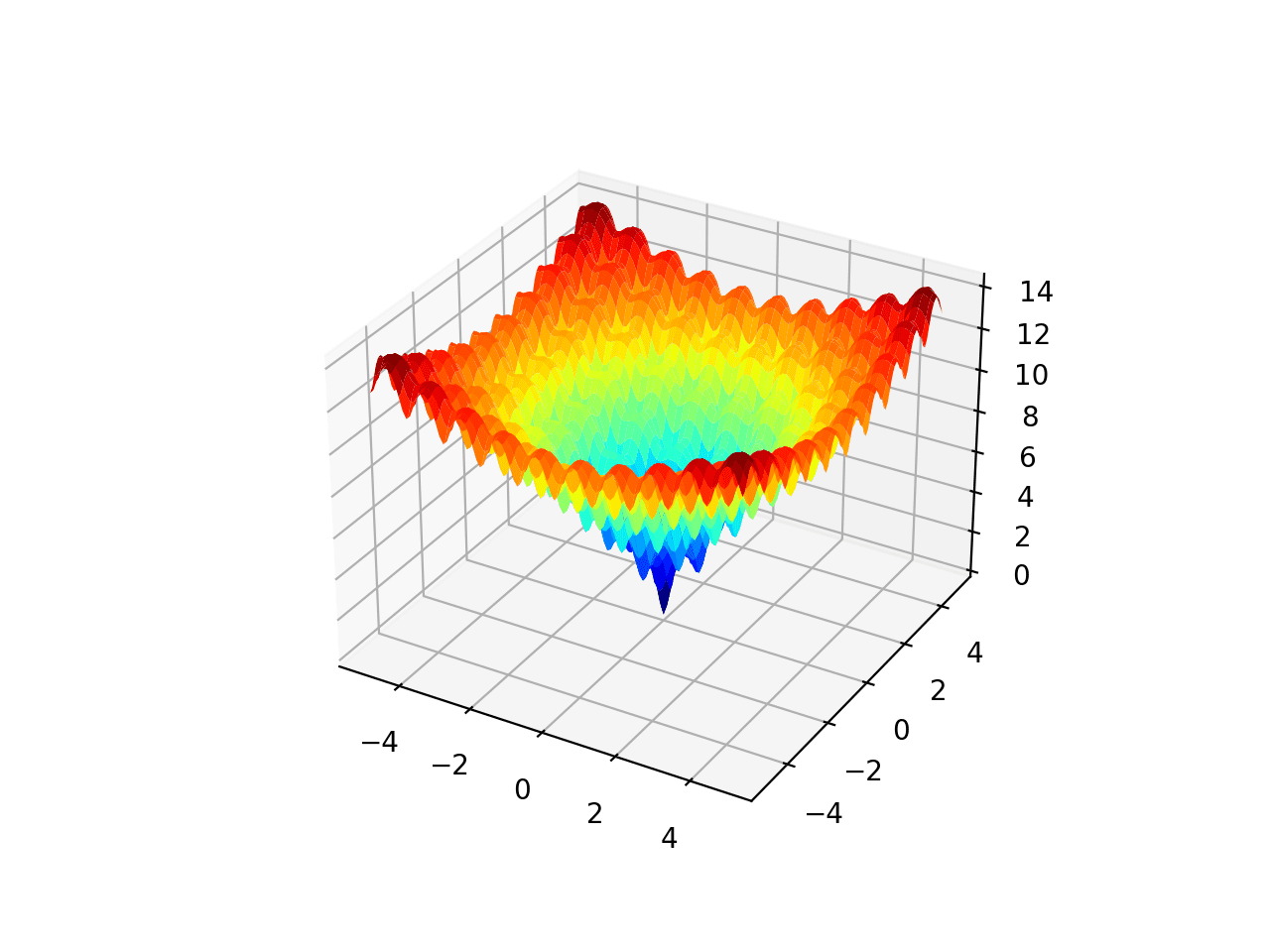
多峰优化函数 1 的曲面图
多峰函数 2
范围被限制在-5.0到5.0之间,四个全局最优值位于[3.0, 2.0]、[-2.805118, 3.131312]、[-3.779310, -3.283186]、[3.584428, -1.848126]。该函数称为Himmelblau 函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 多峰测试函数 from numpy import arange from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return (x**2 + y - 11)**2 + (x + y**2 -7)**2 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建一个函数曲面图。
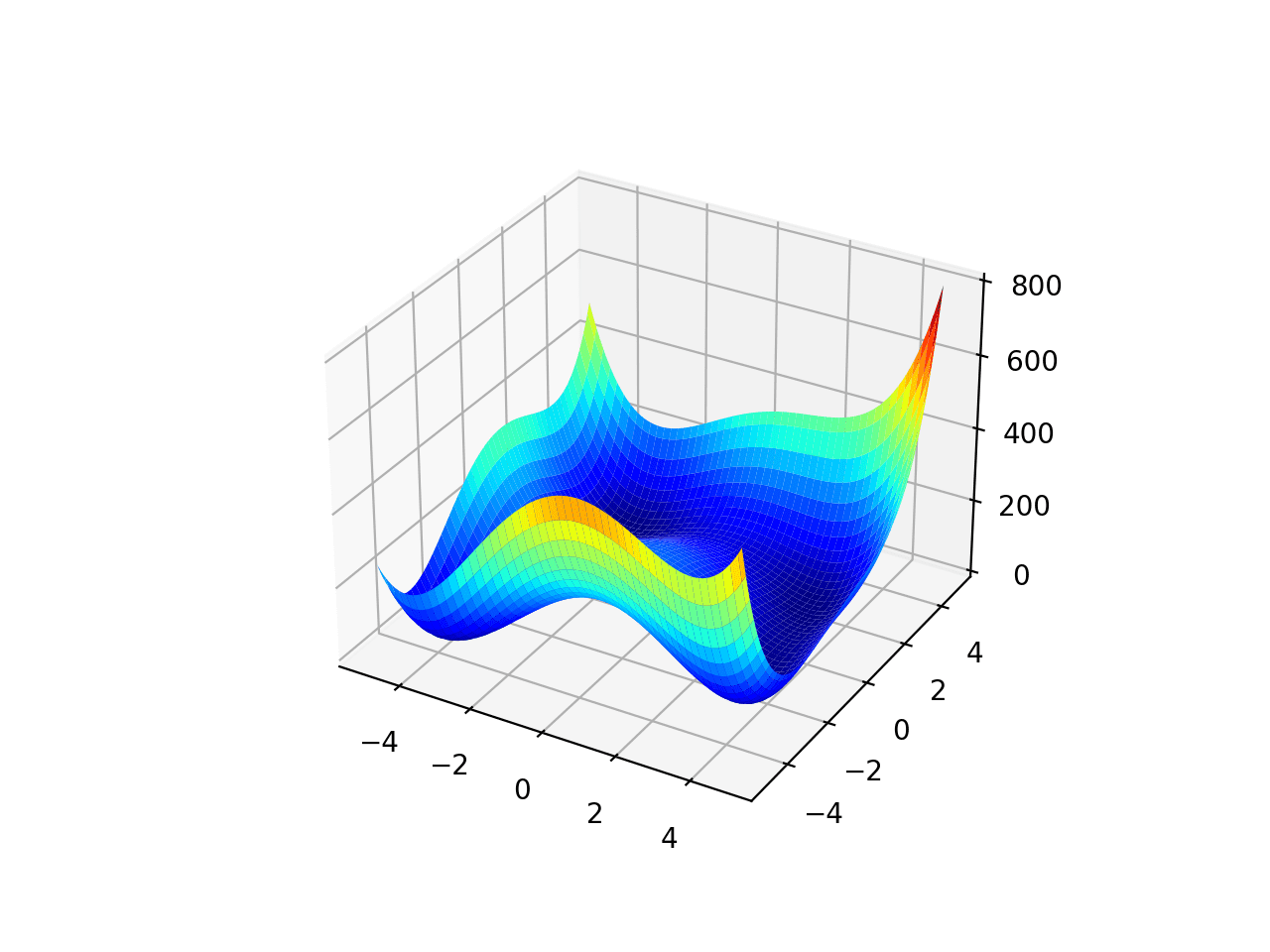
多峰优化函数 2 的曲面图
多峰函数 3
范围被限制在-10.0到10.0之间,该函数有四个全局最优值,分别位于[8.05502, 9.66459]、[-8.05502, 9.66459]、[8.05502, -9.66459]、[-8.05502, -9.66459]。该函数称为 Holder's table 函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 多峰测试函数 from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import sin from numpy import e from numpy import pi from numpy import absolute from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return -absolute(sin(x) * cos(y) * exp(absolute(1 - (sqrt(x**2 + y**2)/pi)))) # 定义输入范围 r_min, r_max = -10.0, 10.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建一个函数曲面图。
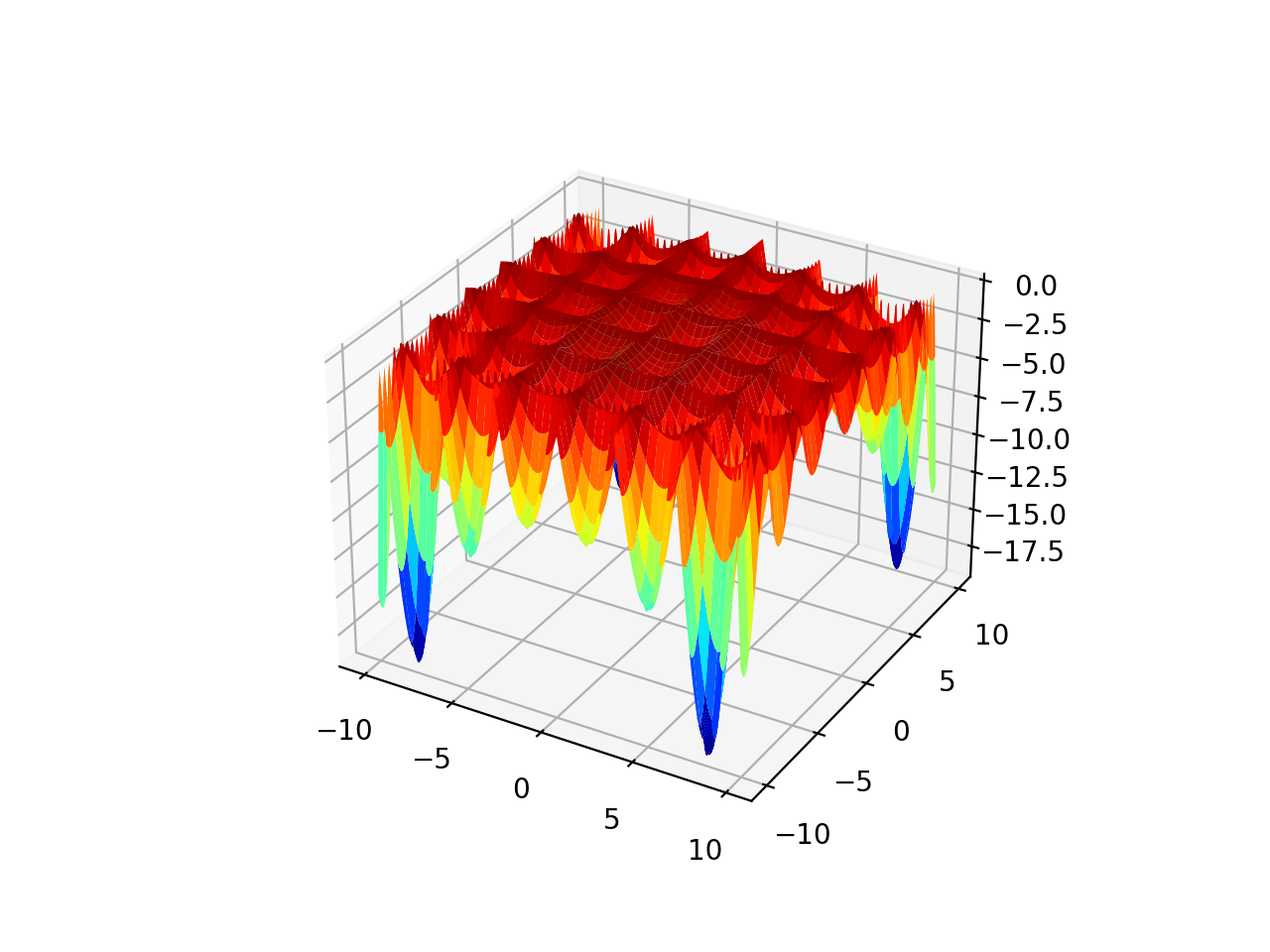
多峰优化函数 3 的曲面图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
总结
在本教程中,您发现了一些标准二维函数,您可以在研究函数优化时使用它们。
您是否使用了以上任何函数?
在下面的评论中告诉我您使用了哪一个。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



感谢这个很棒的补充。但是对于优化算法,需要有一个要传递给该函数的一个解决方案。如何实现这一点?以及如何在给定算法试验中输出的解决方案时绘制这些基准?
谢谢!
不客气。
优化算法将尝试许多候选解决方案来评估目标函数。
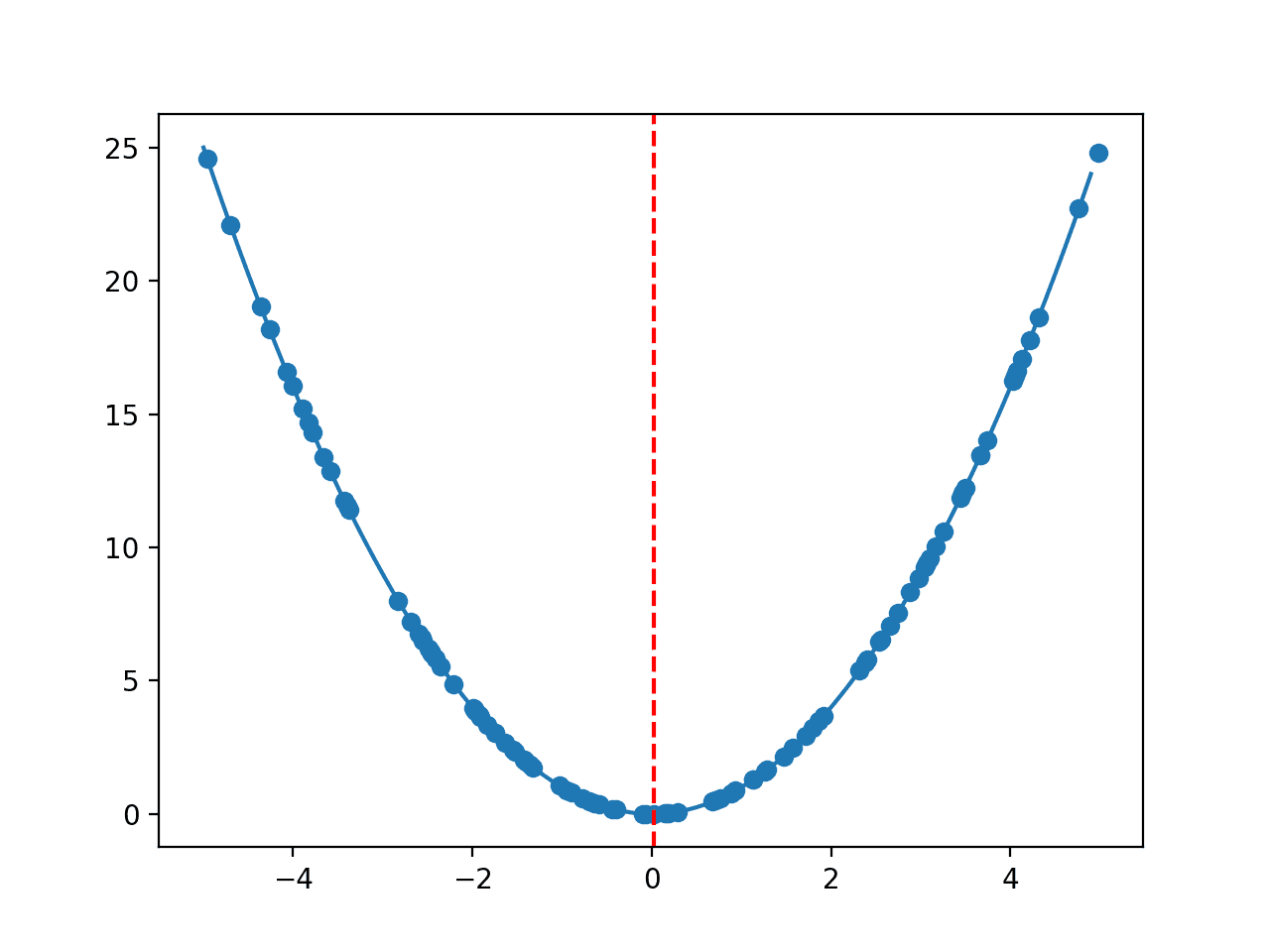
这可以帮助您可视化解决方案
https://machinelearning.org.cn/visualization-for-function-optimization-in-python/
你好,对于 Easom 函数,全局最小值的位置不应该是 [pi,pi] 吗?
我想您说得对。谢谢!
https://en.wikipedia.org/wiki/Test_functions_for_optimization
优化二维板材切割的最佳算法是什么?
损耗最少的算法,我想用这个算法来计算 MDF 的切割。
也许可以尝试一系列算法,然后找出最适合您目标问题的算法。
为什么不试试 CNN-LSTM 呢?
在 eggholder 函数中,
我想计算特定值的输入……
例如,如果我传入输出为 -959.6
它将给出输入 = [512, 404]
请告诉我这是否可能。
您说的是反向优化,或者说是反转问题。我不认为这是可能/可行的。