许多机器学习算法为了达到不同的目的都涉及到优化过程。优化是指通过改变输入值来最小化或最大化目标函数的问题。
优化算法依赖于导数的使用,以了解如何改变(增加或减少)目标函数的输入值,从而实现最小化或最大化。因此,所考虑的目标函数必须是*可微的*。
两个基本三角函数,正弦和余弦,为理解在查找可微函数导数时可能需要进行的运算提供了一个很好的机会。如果我们把它们看作是更复杂函数的基石,那么这两个函数就变得尤为重要。
在本教程中,您将学习如何求正弦和余弦函数的导数。
完成本教程后,您将了解:
- 如何通过应用代数、三角学和极限的若干规则来求正弦和余弦函数的导数。
- 如何在 Python 中求正弦和余弦函数的导数。
让我们开始吧。

正弦和余弦函数的导数
照片由 Tim Marshall 拍摄,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 正弦函数的导数
- 余弦函数的导数
- 在 Python 中求导数
正弦函数的导数
函数 f 在某个特定点 x 处的导数 f’(x) 可以定义为
我们将从正弦函数开始。因此,让我们先代入 f(x) = sin x
如果我们查看三角恒等式,我们会发现我们可以应用*加法公式*来展开 sin(x + h) 项
sin(x + y) = sin x cos y + cos x sin y
事实上,通过将 y 替换为 h,我们可以将 sin x 的导数定义为
通过应用一个极限法则,我们可以进一步简化表达式,该法则规定函数之和的极限等于其极限之和
我们可以通过取出是 x 的函数的任何公因子来进一步简化。通过这种方式,我们可以分解表达式,得到两个不依赖于 x 的单独极限的和
求解这两个极限中的每一个将得到 sin x 的导数。
让我们先处理第一个极限。
回忆一下,我们可以用单位圆来表示弧度角 h。那么 h 的正弦值就是通过在与单位圆相交的点处画一条垂直于 x 轴的线 (BC) 来给出的
我们将比较具有夹角 h 的不同扇形和三角形的面积,试图推断 ((sin h) / h) 在 h 值趋近于零时是如何变化的。为此,我们首先考虑扇形 OAB 的面积:
扇形的面积可以根据圆的半径 r 和弧长 AB,h 来定义。由于所考虑的圆是*单位*圆,则 r = 1
扇形 OAB 的面积 = r h / 2 = h / 2
我们可以将我们刚刚找到的扇形 OAB 的面积与同一扇形内的*三角形 OAB* 的面积进行比较。
该三角形的面积根据其高 BC = sin h 和底长 OA = 1 来定义
三角形 OAB 的面积 = (BC) (OA) / 2 = (sin h) / 2
由于我们可以清楚地看到,我们刚刚考虑的三角形 OAB* 的面积小于它所包含的扇形的面积,因此我们可以说:
(sin h) / 2 < h / 2
(sin h) / h < 1
这是我们获得的关于 ((sin h) / h) 行为的第一个信息,它告诉我们其上限值不会超过 1。*
现在让我们考虑第二个三角形 OAB’,它的面积大于扇形 OAB* 的面积。我们可以使用这个三角形来提供关于 ((sin h) / h) 行为的第二个信息,即它的下限值
将相似三角形的性质应用于 OAB’* 与 OCB* 的关系,可以得到我们计算三角形面积所需的边长 B’A* 的信息
B’A / OA = BC / OC = (sin h) / (cos h)
因此,三角形 OAB’* 的面积可以计算为:
三角形 OAB’ 的面积 = (B’A) (OA) / 2 = (sin h) / (2 cos h)
将三角形 OAB’* 的面积与扇形 OAB* 的面积进行比较,我们可以看到前者现在更大
h / 2 < (sin h) / (2 cos h)
cos h < (sin h) / h
这是我们需要的第二个信息,它告诉我们 ((sin h) / h) 的下限值不会低于 cos h。我们也知道,当 h 趋近于 0 时,cos h 的值趋近于 1。
因此,将这两个信息结合起来,我们发现当 h 变得越来越小时,((sin h) / h) 的值本身就被其下限和上限*夹挤*到 1。这确实被称为*夹挤定理*或*三明治定理*。
现在让我们继续处理第二个极限。
通过应用标准的代数规则
我们可以按如下方式处理第二个极限
然后,通过应用三角学中的勾股定理 sin2h = 1 – cos2h,我们可以将此极限表示为正弦函数
然后应用另一个极限法则,该法则规定乘积的极限等于各极限的乘积
我们已经处理了该乘积的第一个极限,并发现它的值为 1。
该乘积的第二个极限的特点是在分母中有一个 cos h,当 h 变小时,它趋近于 1。因此,当 h 趋近于 0 时,第二个极限的分母趋近于 2。另一方面,分子中的正弦项当 h 趋近于 0 时,其值为 0。这导致了第二个极限,也导致了整个乘积极限趋近于 0
将所有内容放在一起,我们最终可以得出以下结论
sin’(x) = (1) (cos x) + (0) (sin x)
sin’(x) = cos x
最后,这就告诉我们 sin x 的导数就是 cos x。
余弦函数的导数
同样,我们可以通过重用我们在求正弦函数导数时获得的知识来计算余弦函数的导数。代入 f(x) = cos x
现在应用*加法公式*来展开 cos(x + h) 项,如下所示:
cos(x + y) = cos x cos y + sin x sin y
这再次导致了两个极限的和
我们可以很快地意识到,我们在求正弦函数的导数过程中已经计算了这两个极限;当 h 的值变小时,第一个极限趋近于 1,而第二个极限趋近于 0
cos’(x) = (1) (-sin x) + (0) (cos x)
cos’(x) = -sin x
最终,这告诉我们 cos x 的导数就是 -sin x。
我们刚刚找到的导数的重要性在于它们定义了在某个特定角度 h 下所考虑函数的*变化率*。例如,如果我们回顾周期性正弦函数的图形,我们可以观察到它的第一个正峰与 π / 2 弧度角重合。
我们可以使用正弦函数的导数来直接计算图中此峰值的变化率或切线斜率
sin’(π / 2) = cos(π / 2) = 0
我们发现这个结果与正弦函数峰值确实是一个变化率为零的驻点的事实非常吻合。
对于正弦和余弦函数,可以轻松地进行类似的练习来计算不同角度下的切线变化率。
在 Python 中求导数
在本节中,我们将学习如何在 Python 中求正弦和余弦函数的导数。
为此,我们将使用 SymPy 库,它允许我们对数学对象进行符号计算。这意味着 SymPy 库允许我们以符号形式定义和处理正弦和余弦函数,其中变量未求值。我们可以通过使用 Python 中的 symbols 来将变量定义为符号,而求导数则使用 diff 函数。
在继续之前,让我们先加载所需的库。
|
1 2 3 4 |
from sympy import diff from sympy import sin from sympy import cos from sympy import symbols |
现在,我们可以继续以符号形式定义变量 x,这意味着我们可以使用 x 而无需为其赋值。
|
1 2 |
# 将变量定义为符号 x = symbols('x') |
接下来,我们可以使用 diff 函数来求正弦和余弦函数相对于 x 的导数。
|
1 2 3 |
# 求正弦和余弦相对于 x 的一阶导数 print('正弦的一阶导数是:', diff(sin(x), x)) print('余弦的一阶导数是:', diff(cos(x), x)) |
我们发现 diff 函数正确返回 cos(x) 作为正弦的导数,返回 –sin(x) 作为余弦的导数。
|
1 2 |
正弦的一阶导数是: cos(x) 余弦的一阶导数是: -sin(x) |
diff 函数也可以接受多个导数。例如,我们可以通过传递两次 x 来求正弦和余弦的二阶导数。
|
1 2 3 |
# 求正弦和余弦相对于 x 的二阶导数 print('正弦的二阶导数是:', diff(sin(x), x, x)) print('余弦的二阶导数是:', diff(cos(x), x, x)) |
这意味着,在求二阶导数时,我们是对每个函数的一阶导数求导。例如,为了求正弦函数的二阶导数,我们对 cos(x)(其一阶导数)求导。我们可以通过同样地对 –sin(x)(其一阶导数)求导来求余弦函数的二阶导数。
|
1 2 |
正弦的二阶导数是: -sin(x) 余弦的二阶导数是: -cos(x) |
或者,我们可以将数字 2 传递给 diff 函数,以指示我们有兴趣求二阶导数。
|
1 2 3 |
# 求正弦和余弦相对于 x 的二阶导数 print('正弦的二阶导数是:', diff(sin(x), x, 2)) print('余弦的二阶导数是:', diff(cos(x), x, 2)) |
将所有内容汇总在一起,求正弦和余弦函数导数的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 求正弦和余弦函数的导数 from sympy import diff from sympy import sin from sympy import cos from sympy import symbols # 将变量定义为符号 x = symbols('x') # 求正弦和余弦相对于 x 的一阶导数 print('正弦的一阶导数是:', diff(sin(x), x)) print('余弦的一阶导数是:', diff(cos(x), x)) # 求正弦和余弦相对于 x 的二阶导数 print('\n正弦的二阶导数是:', diff(sin(x), x, x)) print('余弦的二阶导数是:', diff(cos(x), x, x)) # 求正弦和余弦相对于 x 的二阶导数 print('\n正弦的二阶导数是:', diff(sin(x), x, 2)) print('余弦的二阶导数是:', diff(cos(x), x, 2)) |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
总结
在本教程中,您学习了如何求正弦和余弦函数的导数。
具体来说,你学到了:
- 如何通过应用代数、三角学和极限的若干规则来求正弦和余弦函数的导数。
- 如何在 Python 中求正弦和余弦函数的导数。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



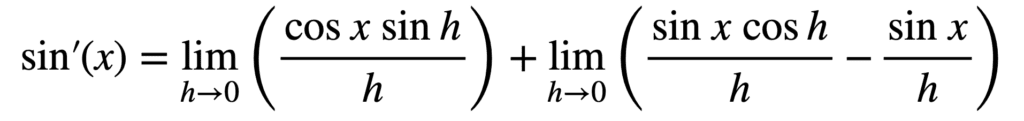
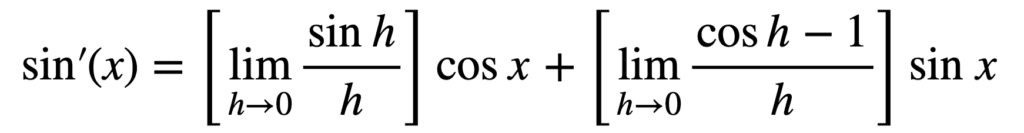







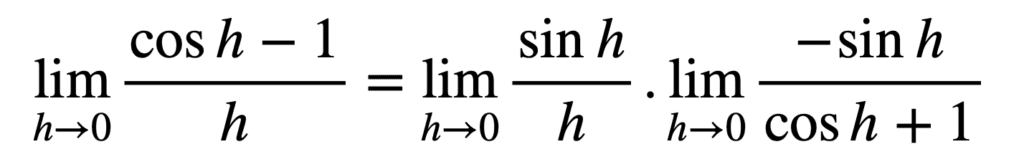











暂无评论。