Python 机器学习矩阵完整指南

Python 机器学习矩阵完整指南
作者 | Ideogram 提供图片

引言

矩阵不仅是线性代数中的一个关键概念，而且在机器学习 (ML) 和数据科学中也得到了广泛的应用。本质上，矩阵是一种用于表示和操作数据的结构化方法，同时它也是机器学习算法中的一个基石元素，用于训练线性回归到神经网络等模型。

本指南将介绍如何在 Python 中定义和使用矩阵、矩阵运算以及它们在机器学习过程中的用途概述。

什么是矩阵？

矩阵是一个二维数组（通俗地说，就是一个集合），它以行-列的方式排列数字。鉴于其结构与由样本和特征组成的表格数据集的相似性，它们在表示数据集、对数据执行转换以及高效执行数学运算方面非常有用。
Python 提供了两种基本方法来实现矩阵：一种是使用嵌套列表，另一种是依赖于 NumPy 库，后者支持优化的矩阵运算。

下面是一个使用列表嵌套列表定义的 3x3 矩阵示例，其中每个嵌套列表代表矩阵的一行

像这样的矩阵可以很好地表示一个包含三个样本的小型数据集，每个样本由三个特征描述。

以下是使用 NumPy 定义矩阵的另一种方法

矩阵基本运算

除了定义包含数据的矩阵之外，矩阵运算在机器学习中对于执行转换、优化和求解线性方程至关重要。例如，训练神经网络的底层过程在很大程度上依赖于这些类型的矩阵运算以及微积分。

让我们从加法和减法开始，概述基本矩阵运算

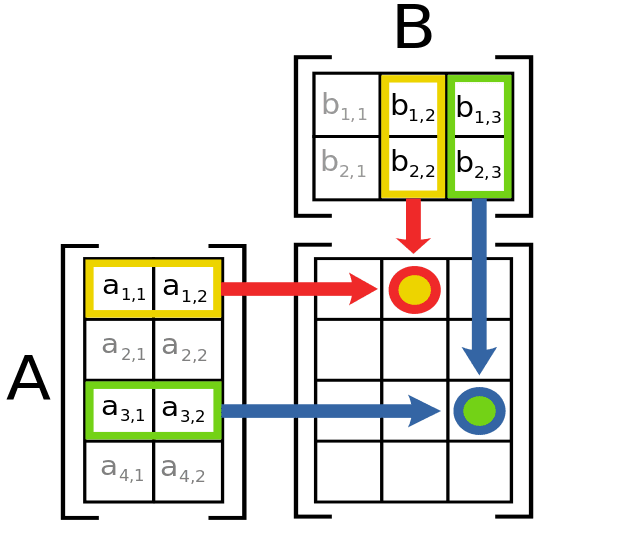
矩阵乘法在机器学习过程中尤为频繁，既用于应用数据转换（如缩放属性），也用于卷积神经网络 (CNN) 等高级神经网络架构，其中矩阵乘法用于对图像数据执行滤波，从而帮助识别视觉数据中的边缘、颜色等模式。Python 中的矩阵乘法执行如下：

但有一个更简单的方法，使用“@”运算符

转置矩阵是机器学习中另一个常见的操作，用于高效地重塑数据或在 PCA（一种众所周知的降维方法）中计算协方差矩阵。

特殊矩阵及其在 Python 机器学习中的作用

是时候识别一些由于其特殊性质而特别重要的矩阵了，这些矩阵在机器学习方法中特别常用。

首先，我们有**单位矩阵**，它在多种机器学习算法中用于数据归一化和转换。此矩阵在其所有元素中包含零，除了主对角线，该对角线由一组成。

与单位矩阵同等重要，甚至更重要的是**逆矩阵**，它是指导大多数机器学习模型训练过程的优化过程的关键。在 Python 中可以通过以下方式轻松计算矩阵的逆：

接下来，**矩阵的行列式**是与矩阵关联的一个值，用于检查矩阵是否为奇异矩阵，如果是，则它没有逆。矩阵必须非零才能可逆。

示例：线性回归中的矩阵

为了完成本入门指南，让我们在机器学习工作流中应用一些学到的概念，特别是在线性回归中。这个非常简单的例子使用**正规方程**解决了线性回归问题，该方程融合了前面看到的一些矩阵运算，即矩阵乘法和逆：W = (X^T X)^{-1} X^T Y。

总结与结论

矩阵在机器学习中有多种用途，包括数据表示、拟合线性回归等模型、通过存储和应用神经元之间连接权重中的运算来训练神经网络，以及在主成分分析 (PCA) 等降维技术中。

由于矩阵是机器学习的核心组成部分，它们得到了 NumPy 等 Python 库的良好支持。本文为初学者提供了关于 Python 机器学习矩阵的基础知识和理解。理解这些基础知识是掌握更高级的机器学习方法和技术关键。