在进行推断统计时,您通常需要检验自己的假设。实际上,有一种方法可以定量检验您所设想的假设。使用艾姆斯住房数据集,您将深入探讨假设检验的概念,并探究空调的存在是否会影响房屋的销售价格。
让我们开始吧。

房地产假设检验:深入探讨艾姆斯住房数据集的假设检验
图片来源:Alex Staudinger。保留部分权利。
概述
本文将通过以下部分展开:
- 假设检验在推断统计中的作用。
- 假设检验如何运作?
- 空调是否影响销售价格?
假设检验在推断统计中的作用
推断统计使用数据样本对来自该样本的总体进行推断。假设检验是推断统计的基本组成部分,在根据样本数据对总体做出明智决策时至关重要,尤其是在研究整个总体不可行时。假设检验是一种对数据做出陈述的方法。
想象一下,您偶然发现一个说法,声称带有空调的房屋比没有空调的房屋售价更高。为了验证这个说法,您将收集房屋销售数据并分析价格是否因空调的存在而存在显著差异。这种使用样本数据检验总体说法或假设的过程称为假设检验。本质上,假设检验允许我们根据样本证据以及观察到的效应偶然发生的可能性,做出明智的决定(拒绝或未能拒绝初始假设)。
通过我的书《数据科学初学者指南》启动您的项目。它提供了带有工作代码的自学教程。
假设检验如何运作?
假设检验是推断统计中的一种方法论方法,您从关于总体参数的初始主张(假设)开始。然后,您使用样本数据来确定是否有足够的证据拒绝这个初始主张。假设检验的组成部分包括:
- 零假设($H_0$):默认状态,表示没有效应或没有差异。您旨在检验的陈述。
- 备择假设($H_a$):您想证明的内容。如果您认为零假设是错误的,这就是您所相信的。
- 检验统计量:根据样本数据计算出的用于检验零假设的值。
- P值:在零假设情况下,样本中观察到的效应由随机机会发生的概率。
进行假设检验就像侦探一样:通常,您假设某事会发生($H_0$),但您怀疑实际发生了其他事情($H_1$)。然后您收集证据(检验统计量)来论证为什么$H_0$不合理;因此$H_1$应该是真相。
在典型的假设检验中:
- 您陈述零假设和备择假设。您应该仔细设计这些假设,以反映对现实的合理假设。
- 您选择一个显著性水平($\alpha$);在统计假设检验中通常使用$\alpha=0.05$。
- 您根据$H_0$的情况收集和分析数据以获得我们的检验统计量和p值。
- 您根据p值做出决定:当且仅当p值小于$\alpha$时,您拒绝零假设并接受备择假设。
让我们看一个如何执行这些步骤的示例。
空调是否影响销售价格?
根据艾姆斯数据集,我们想知道空调的存在是否会影响价格。
为了探究空调对销售价格的影响,您将设置我们的假设为:
- $H_0$:有空调房屋的平均销售价格与没有空调房屋的平均销售价格相同。
- $H_a$:有空调房屋的平均销售价格与没有空调房屋的平均销售价格不同。
在进行假设检验之前,让我们可视化我们的数据以获得初步理解。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# 加载数据集和基本库 import pandas as pd import numpy as np import matplotlib.pyplot as plt Ames = pd.read_csv('Ames.csv') # 数据分离 ac_prices = Ames[Ames['CentralAir'] == 'Y']['SalePrice'] no_ac_prices = Ames[Ames['CentralAir'] == 'N']['SalePrice'] # 设置可视化 plt.figure(figsize=(10, 6)) # 根据空调情况的销售价格直方图 # 首先绘制“有空调”以在图例中获得所需的顺序 plt.hist(ac_prices, bins=30, alpha=0.7, color='blue', edgecolor='blue', lw=0.5, label='Sales Prices With AC') mean_ac = np.mean(ac_prices) plt.axvline(mean_ac, color='blue', linestyle='dashed', linewidth=1.5, label=f'Mean (With AC): ${mean_ac:.2f}') plt.hist(no_ac_prices, bins=30, alpha=0.7, color='red', edgecolor='red', lw=0.5, label='Sales Prices Without AC') mean_no_ac = np.mean(no_ac_prices) plt.axvline(mean_no_ac, color='red', linestyle='dashed', linewidth=1.5, label=f'Mean (Without AC): ${mean_no_ac:.2f}') plt.title('Distribution of Sales Prices based on Presence of Air Conditioning', fontsize=18) plt.xlabel('Sales Price', fontsize=15) plt.ylabel('Number of Houses', fontsize=15) plt.legend(loc='upper right') plt.tight_layout() plt.show() |
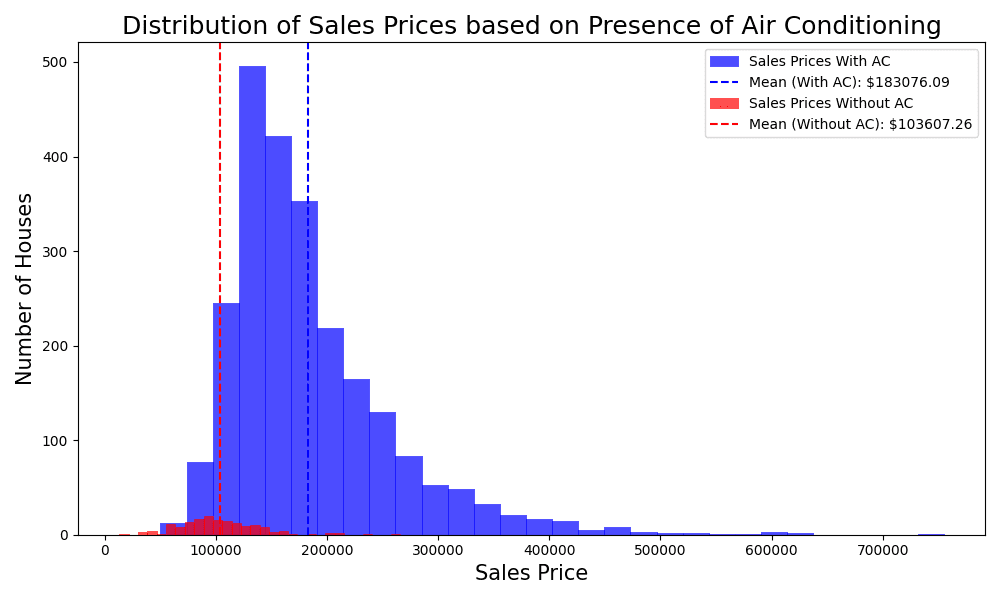
重叠直方图比较销售价格
上面的代码两次调用了plt.hist(),使用了不同的数据,显示了两个重叠的直方图,一个是有空调(AC)的销售价格分布,另一个是没有空调的。以下是一些可以从视觉中得出的观察:
- 明显峰值:两种分布都呈现出明显的峰值,这表明它们各自类别中最常见的销售价格。
- 平均销售价格:有空调房屋的平均销售价格高于没有空调房屋的平均销售价格,如垂直虚线所示。
- 分布和偏度:有空调房屋的销售价格分布略呈右偏,这表明虽然大多数房屋以较低价格出售,但也有一些房产价格明显更高。相比之下,没有空调房屋的分布更紧凑,价格范围更小。
- 重叠:尽管平均值存在差异,但有空调和没有空调房屋的价格范围存在重叠。这表明虽然空调可能会影响价格,但其他因素也在房屋价值的确定中发挥作用。
鉴于这些见解,空调的存在似乎与较高的销售价格相关。下一步将进行假设检验,以数字方式确定这种差异是否显著。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 导入一个额外的库 import scipy.stats as stats # 执行双样本 t 检验 t_stat, p_value = stats.ttest_ind(ac_prices, no_ac_prices, equal_var=False) # 打印结果 if p_value < 0.05: result = "reject the null hypothesis" else: result = "fail to reject the null hypothesis" print(f"With a p-value of {p_value:.5f}, we {result}.") |
这表明:
|
1 |
p值为0.00000,我们拒绝零假设。 |
p值小于$\alpha$。p值表明,在$H_0$下,价格差异极不可能偶然发生。这表明有空调房屋的平均销售价格与没有空调房屋的平均销售价格存在统计学上的显著差异。这与我们从直方图中的视觉观察结果一致。因此,空调的存在确实对艾姆斯数据集中房屋的销售价格产生了显著影响。
此p值是使用 t 检验计算的。它是一种旨在比较两个组的均值的统计量。有许多统计量可用,而 t 检验在此处是合适的,因为我们的假设 $H_0$、$H_a$ 是关于平均销售价格的。
请注意,上面定义的备择假设 $H_a$ 可以更改。您可以将其更改为“有空调房屋的平均销售价格低于没有空调房屋的平均销售价格”;然而,这与现实是反直觉的。您也可以将其更改为“有空调房屋的平均销售价格高于没有空调房屋的平均销售价格”;在这种情况下,您应该更改代码中的 t 检验,添加额外参数alternative='greater'。
|
1 2 3 4 5 6 7 8 9 |
# 执行单侧 t 检验 t_stat, p_value = stats.ttest_ind(ac_prices, no_ac_prices, equal_var=False, alternative='greater') # 打印结果 if p_value < 0.05: result = "reject the null hypothesis" else: result = "fail to reject the null hypothesis" print(f"With a p-value of {p_value:.5f}, we {result}.") |
|
1 |
p-值为 0.00000,我们拒绝零假设。 |
这将双侧 t 检验更改为单侧 t 检验,但结果相同。从双侧 t 检验切换到单侧 t 检验但得出相同的结论意味着我们从一开始就对差异的方向有明确的预期,或者数据强烈支持一个差异方向,使得两种检验类型的结果一致。
零假设($H_0$)和备择假设($H_a$)的设置是统计检验设计的基础,影响检验的方向性(单侧 vs. 双侧)、结果解释(我们如何理解 p 值和证据)以及决策过程(尤其当 p 值接近显著性水平 $\alpha$ 时)。这个框架不仅决定了我们要检验什么,还决定了我们如何解释和利用获得的统计证据。
想开始学习数据科学新手指南吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
进一步阅读
在线资源
资源
总结
在本次探索中,您深入研究了使用艾姆斯住房数据集的假设检验世界。您检查了空调的存在如何影响房屋的销售价格。通过严格的统计检验,您发现有空调的房屋往往比没有空调的房屋具有更高的销售价格,这一结果具有统计显著性。这不仅强调了空调等便利设施在房地产市场中的重要性,而且展示了假设检验在基于数据做出明智决策方面的强大功能。
具体来说,你学到了:
- 假设检验在推断统计中的重要性。
- 如何使用详细的假设检验方法建立和评估零假设和备择假设。
- 假设检验在现实世界场景中的实际意义,以艾姆斯住房市场中空调对房产价值的影响为例。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。







暂无评论。