贝叶斯回归简明入门

作者 Iván Palomares Carrascosa 于 2025年8月27日发布在实用机器学习 0

A Gentle Introduction to Bayesian Regression

贝叶斯回归简明入门
图片由 Editor | ChatGPT 提供

在本文中，您将学习到：

传统回归模型（为其参数使用单一固定值）与贝叶斯回归模型（将参数建模为概率分布）之间的根本区别。
这种概率方法如何让模型能够产生可能结果的完整分布，从而量化其预测中的不确定性。
如何使用 scikit-learn 在 Python 中实现一个简单的贝叶斯回归模型。

引言

在机器学习中，回归模型是一类被广泛用于预测数值型、连续型变量（如房价、温度或股票价值）的模型。传统回归模型由精确的参数或权重定义，并且通常假设这些估计值中没有不确定性。而贝叶斯回归的引入，是为了以概率的方式对预测变量和目标变量之间的关系进行建模，从而在建模过程中引入了不确定性。

传统回归模型

传统回归模型对连续型目标变量（例如房价）的预测结果是一个估计值 $\hat{y}$，这是一个单一、明确的值，例如，将房屋的属性作为输入传递给模型后估算出的房价。例如，一个具有 n 个输入变量（例如房屋属性）的线性回归模型方程由以下线性方程给出：

$\hat{y} = \beta_0 + \beta_1x_1 + \beta_2x_2 + … + \beta_nx_n + \epsilon$

其中 $\epsilon$ 是误差项，$\beta_0, …, \beta_n$ 是与输入变量相关联的权重，再加上一个偏置项 $\beta_0$。这个方程在预测房价的特定学习模型中的一个现实世界的实例可能如下所示：

$\hat{y} = 50000 + 150 \cdot x_1 + 10000 \cdot x_2 – 2000 \cdot x_3 + \epsilon$

其中

$x_1$ 是房屋的面积，单位为平方米。
$x_2$ 是卧室的数量。
$x_3$ 是房屋的年龄，单位为年——请注意该特征权重的负号，这意味着房龄越老，预测价格越低。这是合理的，因为旧房子通常更便宜。

上述模型中的 50000、150、10000 和 -2000 是其参数值或权重。在我们继续讨论时，请记住这一点。

贝叶斯回归是如何工作的？

那么，是什么让贝叶斯回归与此不同呢？与传统回归返回单个值作为预测估计，并且权重也作为精确值被学习不同，贝叶斯回归模型处理的是可能参数值的概率分布，从而将预测中的不确定性考虑在内。换句话说，在贝叶斯回归模型中，每个权重 $\beta_i$ 都变成了一个具有其相关概率分布的随机变量。

学习过程也相应地进行了调整：我们不再寻求一组“最佳拟合”的 n+1 个权重 $\beta_0, \beta_1, \beta_2, …, \beta_n$，而是尝试在给定训练数据（一组具有已知输出或目标值的实例）的情况下，找到参数的后验分布。

重要的是，由于权重被建模为分布，最终的预测 $\hat{y}$ 也变成了分布，而不是明确的、单点的估计值。因此，预测变得不确定。

为什么我们对不确定的预测而不是精确的预测感兴趣？

在某些场景中，理解和解释不确定性与做出预测本身同等重要，这时贝叶斯回归就很有意义。例如，在医疗诊断等高风险场景中，我们可能不仅想知道模型的预测是什么，还想知道模型对该预测的信心或不确定性有多大。在信心较低的情况下，医疗专业人员可以运用他们的专业判断来解释结果。贝叶斯回归能够增加实用价值的其他场景还包括自动驾驶汽车和金融预测：在这些情况下，基于可能错误的精确预测做出决策可能会产生巨大成本或导致危险后果；因此，将预测建模为概率分布是一种更具信息量的方法，可以平衡可能的风险，或在必要时寻求额外信息。

贝叶斯回归：一个简单的例子

让我们用一个非常简单的例子来理解贝叶斯回归是如何工作的。

假设我们只想根据一个属性来估计房屋的价格：它的面积。输入属性用 $x_1$ 表示。这个问题的经典回归模型可能如下所示：

$\hat{y} = 50000 + 150 \cdot x_1$

在贝叶斯回归中，两个模型权重 $\beta_0$ 和 $\beta_1$ 不取 50000 和 150 这样的精确值，而是作为概率分布被学习。例如：

偏置项（也称为截距）$\beta_0$ 服从正态分布，即：
$\beta_0 \sim N(50000, 5000^2)$
同时，单个输入特征的斜率或权重 $\beta_1$ 也变成一个正态分布，即：
$\beta_1 \sim N(150, 20^2)$

回想一下，定义一个正态分布的两个参数是它的均值和方差。

那么房价是如何预测的呢？模型不是返回一个单一的价格预测，而是通过从这两个与权重相关的分布中采样来进行推断，从而产生一系列可能的预测。例如，对于一栋 100 平方米的房子，两个样本可能如下所示：

样本 1：$\beta_0 = 52000$，$\beta_1 = 160$，价格为 $\hat{y} = 52000 + 160 \cdot 100 = 68,000$ 美元
样本 2：$\beta_0 = 49000$，$\beta_1 = 140$，价格为 $\hat{y} = 49000 + 140 \cdot 100 = 63,000$ 美元

通过大量采样，我们最终得到一个预测价格的分布，其中某些价格范围会比其他范围更频繁地出现，因此具有更高的概率。基于此，我们可以将预测表述为置信区间，例如：

这栋房子的预测价值约为 65,500 美元，95% 的置信区间在 61,000 美元到 70,000 美元之间。

如前所述，在一些现实世界的用例中，这些不确定的预测更有价值，有助于做出有效和明智的决策。

使用 Scikit-learn 在 Python 中实现贝叶斯回归

幸运的是，使用 scikit-learn 在 Python 中实现贝叶斯回归非常简单。linear_model 模块提供了一个 BayesianRidge 对象，可用于执行贝叶斯回归。这个对象的工作方式与其他 scikit-learn 模型类似：您创建一个模型实例，用训练数据拟合它，然后用它来进行预测。然而，一个关键的区别是，当您调用 predict 方法时，您还可以请求预测的标准差，这为您提供了一个模型不确定性的度量。

下面是一个简单的代码示例，演示如何使用 BayesianRidge 对一些样本数据进行模型拟合，然后进行预测，包括不确定性。

import numpy as np
from sklearn.linear_model import BayesianRidge

np.random.seed(42)

# Sample data (house square footage) with added noise to demonstrate uncertainty
X = np.array([[50], [100], [150], [200], [250]])

# Target values (house prices) with added random noise
y = (np.array([100000, 200000, 300000, 400000, 500000]) + np.random.normal(0, 30000, X.shape[0]))

# Create and fit the model with adjusted parameters to emphasize uncertainty
# alpha_1, alpha_2, lambda_1, lambda_2 control the prior distributions over precision of weights and noise
model = BayesianRidge(alpha_1=1e-6, alpha_2=1e-6, lambda_1=1e-6, lambda_2=1e-6)
model.fit(X, y)

# Predict the price and uncertainty for a new 120 m^2 house
new_house_sqft = np.array([[120]])
mean_prediction, std_prediction = model.predict(new_house_sqft, return_std=True)

print(f"Predicted price for 120 m^2: ${mean_prediction[0]:,.2f}")
print(f"Uncertainty (std dev) for 120 m^2: ${std_prediction[0]:,.2f}")

# Predict for an extrapolated value to show increased uncertainty (350 m^2)
extrapolated_sqft = np.array([[350]])
mean_extrapolated, std_extrapolated = model.predict(extrapolated_sqft, return_std=True)
print(f"Predicted price for 350 m^2 (extrapolated): ${mean_extrapolated[0]:,.2f}")
print(f"Uncertainty (std dev) for 350 m^2: ${std_extrapolated[0]:,.2f}")

import numpy as np

from sklearn.linear_model import BayesianRidge

np.random.seed(42)

# 样本数据（房屋面积），添加了噪声以演示不确定性

X = np.array([[50], [100], [150], [200], [250]])

# 目标值（房价），添加了随机噪声

y = (np.array([100000, 200000, 300000, 400000, 500000]) + np.random.normal(0, 30000, X.shape[0]))

# 创建并拟合模型，调整参数以强调不确定性

# alpha_1, alpha_2, lambda_1, lambda_2 控制权重和噪声精度的先验分布

model = BayesianRidge(alpha_1=1e-6, alpha_2=1e-6, lambda_1=1e-6, lambda_2=1e-6)

model.fit(X, y)

# 预测一栋 120 平方米新房子的价格和不确定性

new_house_sqft = np.array([[120]])

mean_prediction, std_prediction = model.predict(new_house_sqft, return_std=True)

print(f"120 平方米预测价格：${mean_prediction[0]:,.2f}")

print(f"120 平方米不确定性（标准差）：${std_prediction[0]:,.2f}")

# 对一个外推值进行预测，以显示增加的不确定性（350 平方米）

extrapolated_sqft = np.array([[350]])

mean_extrapolated, std_extrapolated = model.predict(extrapolated_sqft, return_std=True)

print(f"350 平方米预测价格（外推）：${mean_extrapolated[0]:,.2f}")

print(f"350 平方米不确定性（标准差）：${std_extrapolated[0]:,.2f}")

输出

Predicted price for 120 m^2: $253,679.60
Uncertainty (std dev) for 120 m^2: $26,625.02
Predicted price for 350 m^2 (extrapolated): $714,373.37
Uncertainty (std dev) for 350 m^2: $51,462.04

120 平方米预测价格： $253,679.60

120 平方米不确定性（标准差）： $26,625.02

350 平方米预测价格（外推）： $714,373.37

350 平方米不确定性（标准差）： $51,462.04

在上面的代码中：

alpha_1：通过影响模型的权重，设定我们对输入和输出之间关系应有的简单或复杂程度的初始假设。
alpha_2：与 alpha_1 协同工作，控制模型在多大程度上坚持其关于关系简单性的初始假设，而不是从数据中学习。
lambda_1：设定我们对训练数据中存在多少“噪声”或随机误差的初始假设。
lambda_2：与 lambda_1 协同工作，控制模型在多大程度上坚持其关于噪声水平的初始假设。

下面的可视化图表显示了训练数据中的噪声、最佳拟合线，以及最重要的一点：当我们远离训练数据点时，尤其是在外推时，不确定性带是如何变宽的。这直观地展示了贝叶斯回归的核心优势：其量化预测不确定性的能力。

import matplotlib.pyplot as plt

# Generate a wider range of square footage values for plotting, including extrapolation
X_plot = np.linspace(0, 400, 200).reshape(-1, 1)

# Get the mean and standard deviation of the predictions for the plot
y_mean, y_std = model.predict(X_plot, return_std=True)

# Plot the results
plt.figure(figsize=(10, 6))

# Plot the original noisy data points
plt.scatter(X, y, color='blue', label='Training Data (with noise)')

# Plot the regression line
plt.plot(X_plot, y_mean, color='red', label='Bayesian Ridge Mean Prediction')

# Plot the uncertainty area (1 standard deviation)
plt.fill_between(X_plot.ravel(), y_mean - y_std, y_mean + y_std, color='pink', alpha=0.5, label='Uncertainty (1 std dev)')

# Plot the 95% confidence interval (approx. 2 std dev) for richer illustration
plt.fill_between(X_plot.ravel(), y_mean - 2 * y_std, y_mean + 2 * y_std, color='lightcoral', alpha=0.2, label='Uncertainty (2 std dev / 95% CI)')

# Visualization labels and presentation
plt.title('Bayesian Regression with Quantified Uncertainty')
plt.xlabel('Square Footage')
plt.ylabel('House Price')
plt.legend()
plt.grid(True)
plt.show()

import matplotlib.pyplot as plt

# 生成更宽范围的面积值用于绘图，包括外推

X_plot = np.linspace(0, 400, 200).reshape(-1, 1)

# 获取绘图用预测的均值和标准差

y_mean, y_std = model.predict(X_plot, return_std=True)

# 绘制结果

plt.figure(figsize=(10, 6))

# 绘制原始带噪声的数据点

plt.scatter(X, y, color='blue', label='训练数据（含噪声）')

# 绘制回归线

plt.plot(X_plot, y_mean, color='red', label='贝叶斯岭回归均值预测')

# 绘制不确定性区域（1个标准差）

plt.fill_between(X_plot.ravel(), y_mean - y_std, y_mean + y_std, color='pink', alpha=0.5, label='不确定性（1个标准差）')

# 绘制 95% 置信区间（约 2 个标准差）以丰富图示

plt.fill_between(X_plot.ravel(), y_mean - 2 * y_std, y_mean + 2 * y_std, color='lightcoral', alpha=0.2, label='不确定性（2个标准差 / 95% 置信区间）')

# 可视化标签和展示

plt.title('带量化不确定性的贝叶斯回归')

plt.xlabel('房屋面积')

plt.ylabel('房价')

plt.legend()

plt.grid(True)

plt.show()

以及我们生成的可视化图表

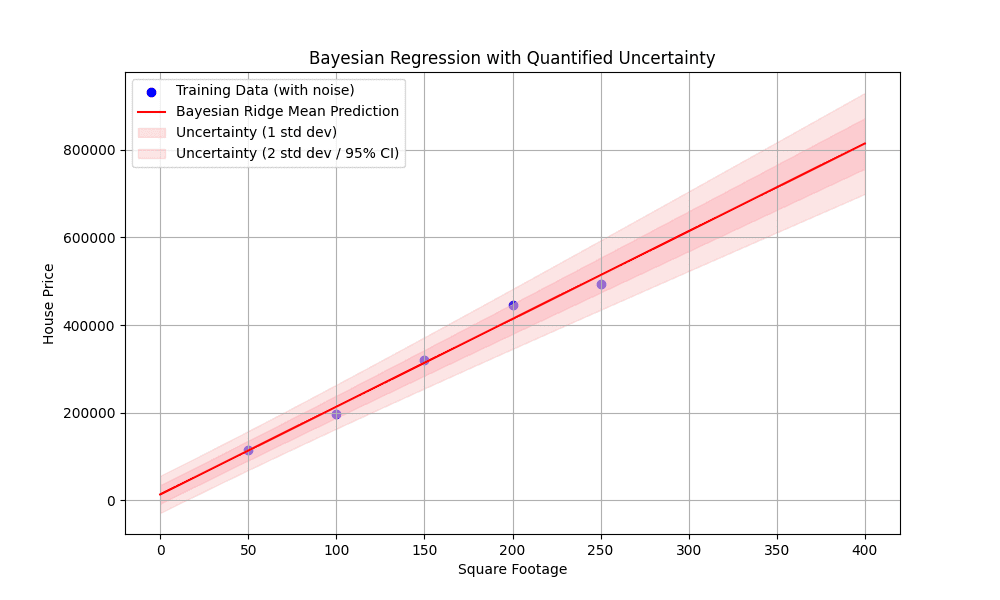
Figure 1: Bayesian regression with quantified uncertainty

图1：带量化不确定性的贝叶斯回归

总结

贝叶斯回归可以被视为经典回归模型的不确定性和概率性对应物，而经典回归模型是在许多现实世界应用中进行预测的最广泛使用的机器学习模型之一。本文对这种回归技术的基础知识和实用性进行了简要介绍。

对特定的贝叶斯回归技术和模型感兴趣吗？其中最受欢迎的有贝叶斯线性回归、贝叶斯岭回归和高斯过程回归（GPR）。

导航

贝叶斯回归简明入门

引言

传统回归模型

贝叶斯回归是如何工作的？

贝叶斯回归：一个简单的例子

使用 Scikit-learn 在 Python 中实现贝叶斯回归

总结

关于此主题的更多信息

暂无评论。

发表评论点击这里取消回复。

导航

引言

传统回归模型

贝叶斯回归是如何工作的？

贝叶斯回归：一个简单的例子

使用 Scikit-learn 在 Python 中实现贝叶斯回归

总结

关于此主题的更多信息

暂无评论。

发表评论 点击这里取消回复。

发表评论点击这里取消回复。