计算正态汇总统计量的温和介绍

作者 Jason Brownlee 发布于 2019 年 8 月 8 日在统计学 21

数据样本是更广泛的总体中的一个快照，该总体包含所有可能从某个领域获取或由某个过程生成的所有观察结果。

有趣的是，许多观察结果符合一种常见的模式或分布，称为正态分布，或更正式地称为高斯分布。关于高斯分布的知识很多，因此，统计学和统计方法中有一些专门的子领域可以用于高斯数据。

在本教程中，您将了解高斯分布，如何识别它，以及如何计算从该分布中提取数据的关键汇总统计量。

完成本教程后，您将了解：

高斯分布描述了许多观测值，包括在应用机器学习中看到的许多观测值。
分布的集中趋势是最可能的观测值，可以从数据样本中估计为均值或中位数。
方差是分布中与均值的平均偏差，可以从数据样本中估计为方差和标准差。

通过我的新书《机器学习统计学》启动您的项目，其中包括分步教程和所有示例的 Python 源代码文件。

让我们开始吧。

A Gentle Introduction to Calculating Normal Summary Statistics

计算正态汇总统计量的温和介绍
照片来自约翰，保留部分权利。

教程概述

本教程分为6个部分；它们是

高斯分布
样本与总体
测试数据集
集中趋势
方差
描述高斯分布

需要机器学习统计学方面的帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

高斯分布

数据分布指的是当您绘制图表（例如直方图）时它所具有的形状。

最常见且因此最知名的连续值分布是钟形曲线。它被称为“正态”分布，因为它有大量数据落入此分布中。它也更正式地被称为高斯分布，以卡尔·弗里德里希·高斯的名字命名。

因此，您会看到数据呈正态分布或高斯分布的引用，它们可以互换使用，都指同一件事：数据看起来像高斯分布。

一些具有高斯分布的观测值示例包括

人的身高。
智商分数。
体温。

让我们看看正态分布。下面是一些生成和绘制理想高斯分布的代码。

# generate and plot an idealized gaussian
from numpy import arange
from matplotlib import pyplot
from scipy.stats import norm
# x-axis for the plot
x_axis = arange(-3, 3, 0.001)
# y-axis as the gaussian
y_axis = norm.pdf(x_axis, 0, 1)
# plot data
pyplot.plot(x_axis, y_axis)
pyplot.show()

# 生成并绘制理想高斯分布

from numpy import arange

from matplotlib import pyplot

from scipy.stats import norm

# 绘图的 x 轴

x_axis = arange(-3, 3, 0.001)

# y 轴作为高斯分布

y_axis = norm.pdf(x_axis, 0, 1)

# 绘制数据

pyplot.plot(x_axis, y_axis)

pyplot.show()

运行示例会生成理想高斯分布的图。

x 轴是观测值，y 轴是每个观测值的频率。在这种情况下，0.0 附近的观测值最常见，而 -3.0 和 3.0 附近的观测值则很少见或不太可能。

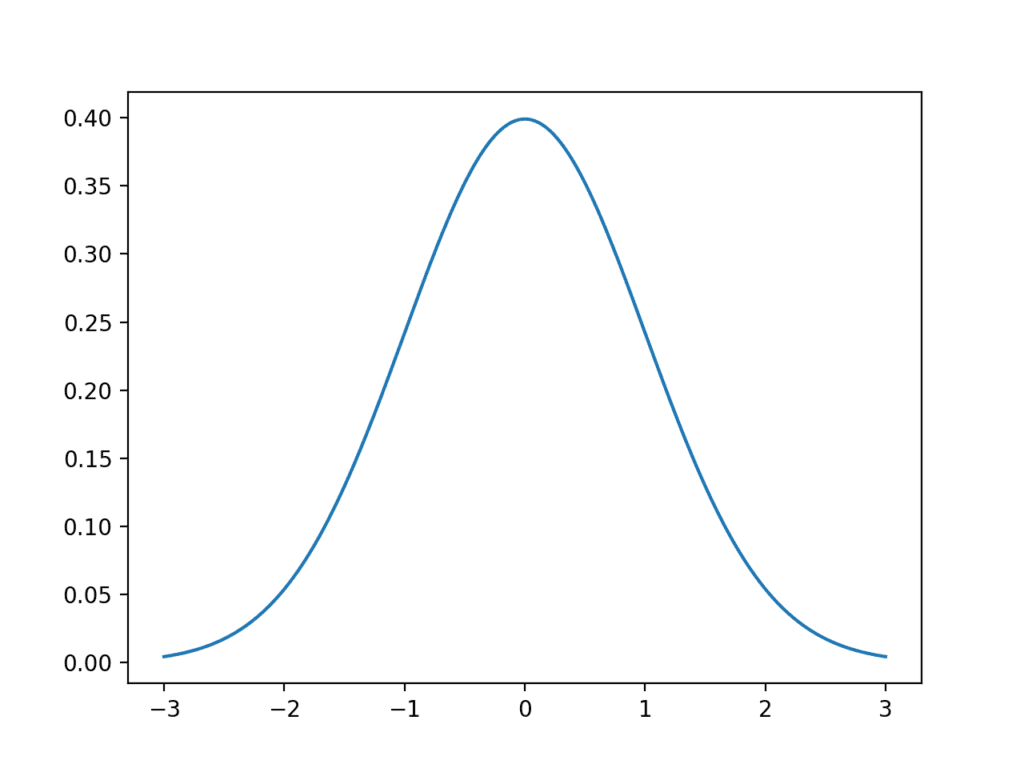
高斯分布的折线图

当数据是高斯分布时，或者当我们假设高斯分布来计算统计量时，这会很有帮助。这是因为高斯分布非常 хорошо understood。以至于统计学领域的很大一部分致力于这种分布的方法。

幸运的是，我们在机器学习中处理的许多数据通常都符合高斯分布，例如我们可能用于拟合模型的输入数据，以及模型在不同训练数据样本上重复评估的结果。

并非所有数据都是高斯分布，有时通过查看数据的直方图或使用统计检验进行检查来发现这一点很重要。一些不符合高斯分布的观测值示例包括

人们的收入。
城市人口。
图书销量。

样本与总体

我们可以认为数据是由某种未知过程生成的。

我们收集到的数据称为数据样本，而所有可能收集到的数据称为总体。

数据样本：来自一个组的观测值子集。
数据总体：来自一个组的所有可能的观测值。

这是一个重要的区别，因为不同的统计方法用于样本和总体，而在应用机器学习中，我们通常处理数据样本。如果您在谈论机器学习中的数据时读到或使用“总体”一词，那么在统计方法方面，它很可能意味着样本。

您在机器学习中会遇到的两个数据样本示例包括

训练集和测试集。
模型的性能分数。

在使用统计方法时，我们经常希望仅使用样本中的观测值来对总体进行声明。

两个明确的例子包括

训练样本必须代表观测总体，以便我们可以拟合一个有用的模型。
测试样本必须代表观测总体，以便我们可以对模型技能进行无偏评估。

因为我们正在使用样本并对总体进行声明，这意味着总是存在一些不确定性，并且理解和报告这种不确定性很重要。

测试数据集

在我们探讨具有高斯分布数据的一些重要汇总统计量之前，让我们首先生成一个可以处理的数据样本。

我们可以使用 randn() NumPy 函数生成一个从高斯分布中提取的随机数样本。

有定义任何高斯分布的两个关键参数；它们是均值和标准差。我们将在后面更详细地介绍这些参数，因为当数据从未知高斯分布中提取时，它们也是要估计的关键统计量。

randn() 函数将生成指定数量的随机数（例如 10,000），这些随机数从均值为零和标准差为 1 的高斯分布中提取。然后我们可以通过重新缩放这些数字，将它们缩放到我们选择的高斯分布。

这可以通过添加期望的均值（例如 50）并将值乘以标准差（5）来保持一致。

data = 5 * randn(10000) + 50

1	数据 = 5 * randn(10000) + 50

然后我们可以使用直方图绘制数据集，并寻找绘制数据预期的形状。

完整的示例如下所示。

# generate a sample of random gaussians
from numpy.random import seed
from numpy.random import randn
from matplotlib import pyplot
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(10000) + 50
# histogram of generated data
pyplot.hist(data)
pyplot.show()

# 生成高斯随机数样本

from numpy.random import seed

from numpy.random import randn

from matplotlib import pyplot

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

数据 = 5 * randn(10000) + 50

# 生成数据的直方图

pyplot.hist(数据)

pyplot.show()

运行示例会生成数据集并将其绘制为直方图。

我们几乎可以看到数据的高斯形状，但它有点块状。这突出了一点。

有时，数据不会是完美的高斯分布，但它会具有高斯状分布。它几乎是高斯分布，如果以不同的方式绘制、以某种方式缩放或收集更多数据，它可能会更接近高斯分布。

通常，在处理类高斯数据时，我们可以将其视为高斯数据，并使用所有相同的统计工具并获得可靠的结果。

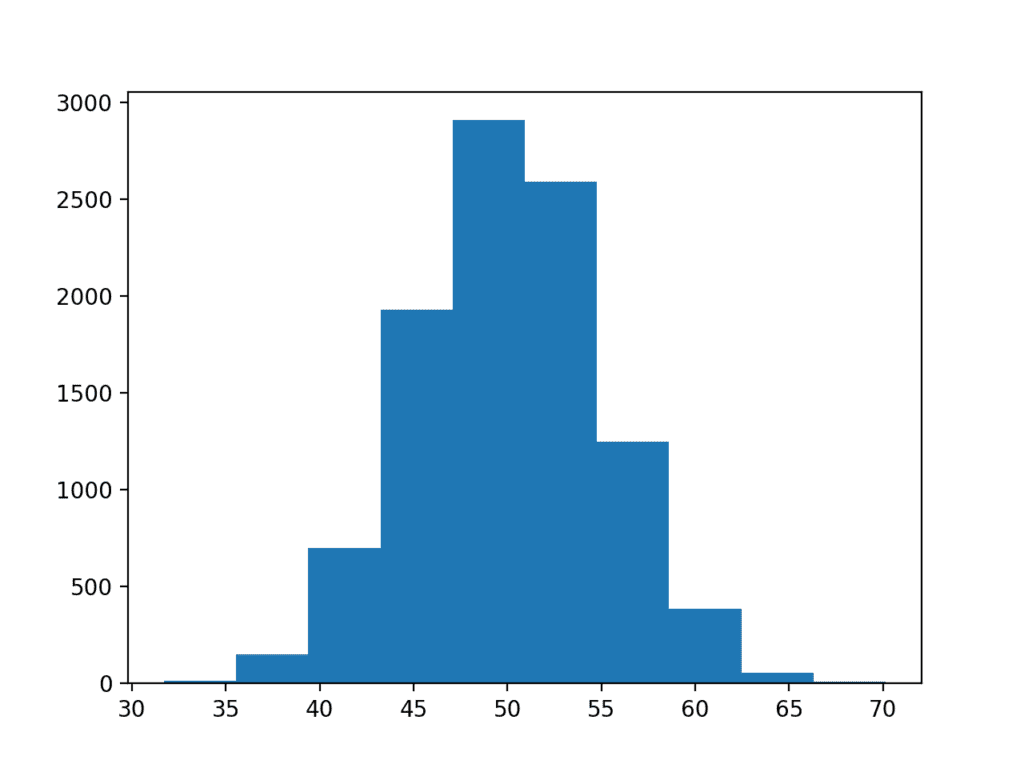
高斯数据集的直方图

在这个数据集的例子中，我们确实有足够的数据，并且图是块状的，因为绘图函数为分割数据选择了任意大小的桶。我们可以选择一种不同、更精细的方式来分割数据，并更好地揭示底层的高斯分布。

下面列出了更新后的示例以及更精细的图。

# generate a sample of random gaussians
from numpy.random import seed
from numpy.random import randn
from matplotlib import pyplot
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(10000) + 50
# histogram of generated data
pyplot.hist(data, bins=100)
pyplot.show()

# 生成高斯随机数样本

from numpy.random import seed

from numpy.random import randn

from matplotlib import pyplot

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

数据 = 5 * randn(10000) + 50

# 生成数据的直方图

pyplot.hist(数据, bins=100)

pyplot.show()

运行示例，我们可以看到选择 100 个数据分割在创建清晰显示数据高斯分布的图方面做得更好。

数据集是从完美的高斯分布生成的，但这些数字是随机选择的，我们只选择了 10,000 个观测值作为样本。您可以看到，即使在这种受控设置下，数据样本中也存在明显的噪声。

这突出另一点：我们应该始终预期数据样本中存在一些噪声或限制。与纯粹的底层分布相比，数据样本将始终包含误差。

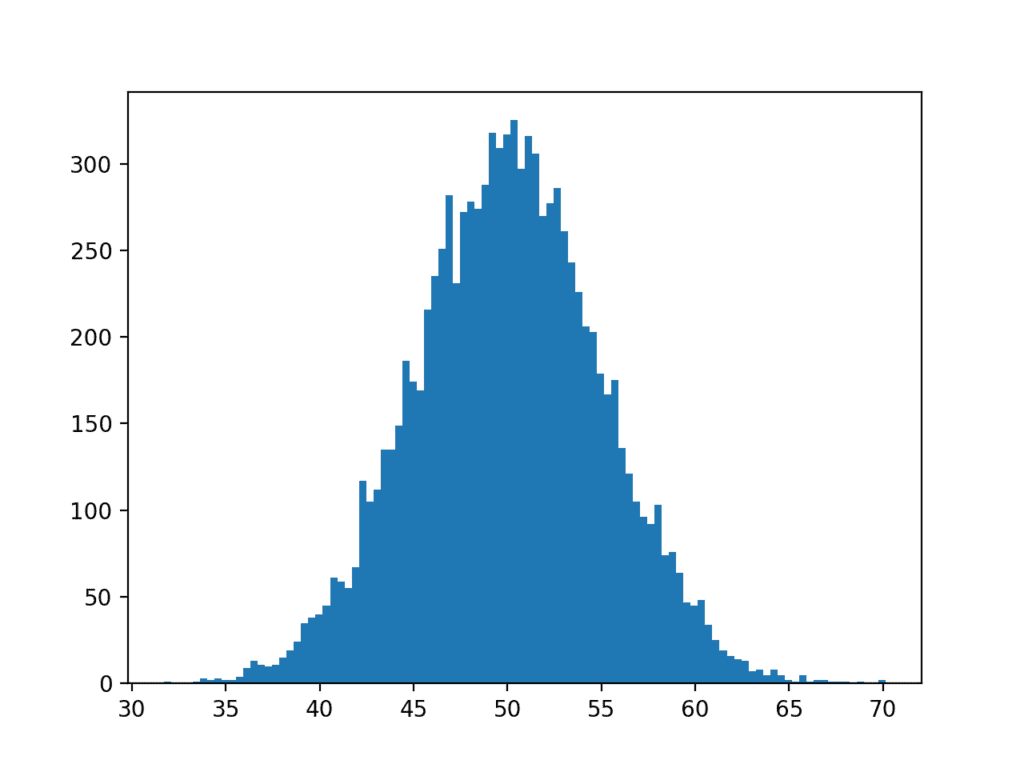
Histogram plot of Gaussian Dataset With More Bins

具有更多 Bin 的高斯数据集直方图

集中趋势

分布的集中趋势指的是分布中的中间值或典型值。最常见或最可能的值。

在高斯分布中，集中趋势称为均值，或更正式地称为算术平均值，是定义任何高斯分布的两个主要参数之一。

样本的均值计算为观测值之和除以样本中观测值的总数。

mean = sum(data) / length(data)

1	均值 = sum(数据) / length(数据)

它也以更紧凑的形式书写为

mean = 1 / length(data) * sum(data)

1	均值 = 1 / length(数据) * sum(数据)

我们可以通过在数组上使用 mean() NumPy 函数来计算样本的均值。

result = mean(data)

1	result = mean(数据)

下面的示例演示了在上一节中开发的测试数据集上的应用。

# calculate the mean of a sample
from numpy.random import seed
from numpy.random import randn
from numpy import mean
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(10000) + 50
# calculate mean
result = mean(data)
print('Mean: %.3f' % result)

# 计算样本的均值

from numpy.random import seed

from numpy.random import randn

from numpy import mean

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

数据 = 5 * randn(10000) + 50

# 计算均值

result = mean(数据)

print('均值: %.3f' % result)

运行示例会计算并打印样本的均值。

样本算术平均值的计算是对样本所来自的总体基础高斯分布参数的估计。作为估计，它将包含误差。

因为我们知道基础分布的真实平均值为 50，所以我们可以看到从 10,000 个观测样本中得出的估计值相当准确。

Mean: 50.049

1	平均值：50.049

均值容易受到异常值的影响，即远离均值的罕见值。这些可能是分布边缘上合法罕见的观测值或错误。

此外，均值可能具有误导性。在另一种分布（例如均匀分布或幂分布）上计算均值可能没有多大意义，因为尽管可以计算该值，但它将指的是一个看似任意的期望值，而不是分布的真实集中趋势。

在存在异常值或非高斯分布的情况下，另一种常用且易于计算的集中趋势是中位数。

中位数通过首先对所有数据进行排序，然后找到样本中的中间值来计算。如果观测值数量为奇数，则此操作简单。如果观测值数量为偶数，则中位数计算为中间两个观测值的平均值。

我们可以通过调用 median() NumPy 函数来计算数组样本的中位数。

result = median(data)

1	result = median(数据)

下面的示例演示了在测试数据集上的应用。

# calculate the median of a sample
from numpy.random import seed
from numpy.random import randn
from numpy import median
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(10000) + 50
# calculate median
result = median(data)
print('Median: %.3f' % result)

# 计算样本的中位数

from numpy.random import seed

from numpy.random import randn

从 numpy 导入 median

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

数据 = 5 * randn(10000) + 50

# 计算中位数

result = median(数据)

print('中位数: %.3f' % result)

运行示例，我们可以看到中位数是从样本中计算并打印出来的。

由于样本具有高斯分布，结果与均值相差不大。如果数据具有不同的（非高斯）分布，则中位数可能与均值相差很大，并且可能更好地反映基础总体的集中趋势。

Median: 50.042

1	中位数: 50.042

方差

分布的方差是指观测值平均与均值相差或不同的程度。

将方差视为分布的离散度度量很有用。低方差的值将聚集在均值附近（例如窄钟形），而高方差的值将从均值向外扩散（例如宽钟形）。

我们可以通过一个示例来演示这一点，绘制具有低方差和高方差的理想高斯分布。完整的示例列在下面。

# generate and plot gaussians with different variance
from numpy import arange
from matplotlib import pyplot
from scipy.stats import norm
# x-axis for the plot
x_axis = arange(-3, 3, 0.001)
# plot low variance
pyplot.plot(x_axis, norm.pdf(x_axis, 0, 0.5))
# plot high variance
pyplot.plot(x_axis, norm.pdf(x_axis, 0, 1))
pyplot.show()

# 生成并绘制具有不同方差的高斯分布

from numpy import arange

from matplotlib import pyplot

from scipy.stats import norm

# 绘图的 x 轴

x_axis = arange(-3, 3, 0.001)

# 绘制低方差

pyplot.plot(x_axis, norm.pdf(x_axis, 0, 0.5))

# 绘制高方差

pyplot.plot(x_axis, norm.pdf(x_axis, 0, 1))

pyplot.show()

运行示例会绘制两个理想的高斯分布：蓝色曲线表示围绕均值聚集的低方差，橙色曲线表示更分散的高方差。

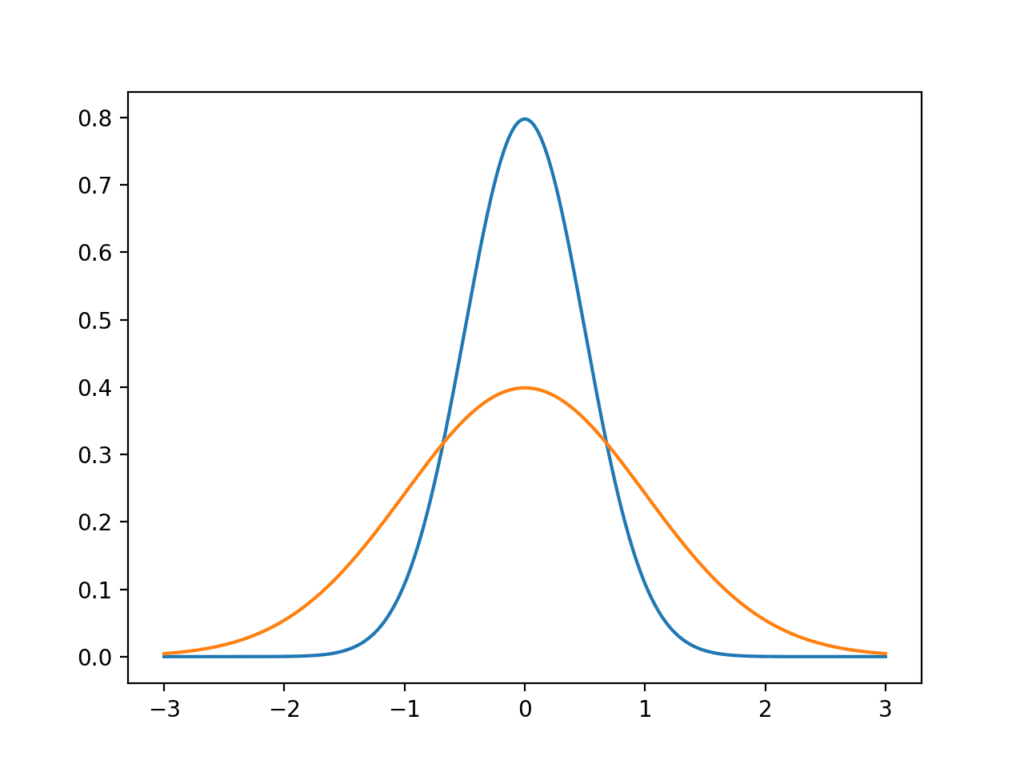
Line plot of Gaussian distributions with low and high variance

低方差和高方差高斯分布的线图

从高斯分布中提取的数据样本的方差计算为样本中每个观测值与样本均值之差的平方的平均值

variance = 1 / (length(data) - 1) * sum(data[i] - mean(data))^2

1	方差 = 1 / (length(数据) - 1) * sum(数据[i] - mean(数据))^2

其中方差通常表示为 s^2，清楚地显示了度量的平方单位。您可能会看到没有（-1）的观测值数量的方程，这是总体方差的计算，而不是样本方差。

我们可以使用 var() 函数在 NumPy 中计算数据样本的方差。

下面的示例演示了在测试问题上计算方差。

# calculate the variance of a sample
from numpy.random import seed
from numpy.random import randn
from numpy import var
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(10000) + 50
# calculate variance
result = var(data)
print('Variance: %.3f' % result)

# 计算样本的方差

from numpy.random import seed

from numpy.random import randn

from numpy import var

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

数据 = 5 * randn(10000) + 50

# 计算方差

result = var(数据)

print('方差: %.3f' % result)

运行示例会计算并打印方差。

Variance: 24.939

方差：24.939

方差很难解释，因为单位是观测值的平方单位。我们可以通过对结果取平方根将单位还原为观测值的原始单位。

例如，24.939 的平方根约为 4.9。

通常，当总结高斯分布的离散度时，使用方差的平方根来描述。这称为标准差。标准差与均值一起是指定任何高斯分布所需的两个关键参数。

我们可以看到 4.9 的值非常接近在为测试问题创建样本时指定的标准差值 5。

我们可以将方差计算包装在平方根中，直接计算标准差。

standard deviation = sqrt(1 / (length(data) - 1) * sum(data[i] - mean(data))^2)

1	标准差 = sqrt(1 / (length(数据) - 1) * sum(数据[i] - mean(数据))^2)

其中标准差通常写作 s 或希腊小写字母 sigma。

可以通过 std() 函数直接在 NumPy 中计算数组的标准差。

下面的示例演示了在测试问题上计算标准差。

# calculate the standard deviation of a sample
from numpy.random import seed
from numpy.random import randn
from numpy import std
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(10000) + 50
# calculate standard deviation
result = std(data)
print('Standard Deviation: %.3f' % result)

# 计算样本的标准差

from numpy.random import seed

from numpy.random import randn

from numpy import std

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

数据 = 5 * randn(10000) + 50

# 计算标准差

result = std(数据)

print('标准差: %.3f' % result)

运行示例会计算并打印样本的标准差。该值与方差的平方根匹配，并且非常接近 5.0，这是问题定义中指定的值。

Standard Deviation: 4.994

标准差：4.994

方差的度量可以为非高斯分布计算，但通常需要识别分布，以便计算特定于该分布的专门方差度量。

描述高斯分布

在应用机器学习中，您通常需要报告算法的结果。

也就是说，报告模型在样本外数据上的估计技能。

这通常通过报告 k 折交叉验证或其他重复抽样过程的平均性能来完成。

在报告模型技能时，您实际上是在总结技能分数的分布，而且很可能技能分数是从高斯分布中提取的。

通常只报告模型的平均性能。这将隐藏模型技能分布的另外两个重要细节。

我建议至少报告模型分数高斯分布的两个参数和样本大小。理想情况下，确认模型技能分数确实是高斯分布或看起来足够高斯以支持报告高斯分布的参数也是一个好主意。

这很重要，因为读者可以重建技能分数的分布，并可能将其与未来相同问题上模型的技能进行比较。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

开发您自己的测试问题并计算集中趋势和方差度量。
开发一个函数来计算给定数据样本的汇总报告。
加载并汇总标准机器学习数据集的变量

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

API

文章

总结

在本教程中，您学习了高斯分布、如何识别它以及如何计算从该分布中提取数据的关键汇总统计量。

具体来说，你学到了：

高斯分布描述了许多观测值，包括在应用机器学习中看到的许多观测值。
分布的集中趋势是最可能的观测值，可以从数据样本中估计为均值或中位数。
方差是分布中与均值的平均偏差，可以从数据样本中估计为方差和标准差。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何在 Python 中计算变量之间的相关性

机器学习中大数定律的温和介绍

21 条对《计算正态汇总统计量的温和介绍》的回复

Sharp Sight 2018 年 4 月 30 日上午 8:05 #

扎实的概述。我通常更喜欢 R 和 tidyverse 进行绘图和分析，但基本 R 中的统计函数有点笨拙。

...Numpy 感觉更直观。

回复
- Jason Brownlee 2018 年 5 月 1 日上午 5:29 #
  
  谢谢。
  
  回复
Bijoy 2018 年 5 月 1 日晚上 8:30 #

嗨 Jason
请给我你的邮箱，我们可以一起工作，我在智能监控系统领域。

回复
- Jason Brownlee 2018 年 5 月 2 日上午 5:37 #
  
  您可以使用联系我页面。
  
  请参阅有关新项目的此内容
  https://machinelearning.org.cn/faq/single-faq/can-you-help-me-with-my-project
  
  回复
kotrappa sirbi 2018 年 5 月 1 日晚上 10:53 #

对高斯分布的精彩介绍，在短时间内完成并在几分钟内练习，谢谢，我想知道它在实际数据科学（特别是在应用机器学习中）有哪些应用

回复
- Jason Brownlee 2018 年 5 月 2 日上午 5:43 #
  
  它可以帮助您在预处理和建模之前了解您的数据。
  
  回复
TOM 2018 年 5 月 4 日上午 7:07 #

嗨，Jason，

你有这本书的教程（统计学）吗？

回复
- Jason Brownlee 2018 年 5 月 4 日上午 7:49 #
  
  是的，我目前正在定稿。
  
  回复

安东尼考拉 2018 年 5 月 4 日下午 3:25 #

尊敬的Jason博士，
我正在查看本教程和另外两个相关教程。
我可以使用以下方法绘制函数

pyplot.plot(x,y); #looks like a continuous plot
pyplot.scatter(x,y) ; #uses symbols for plotting values.

1 2	pyplot.plot(x,y); #看起来像一个连续的图 pyplot.scatter(x,y) ; #使用符号绘制值。

对于直方图，我可以执行以下操作

pyplot.hist(yaxis); #Don't need the xaxis. The no of bins determines how detailed the hist.

1	pyplot.hist(yaxis); #不需要x轴。bin的数量决定了直方图的详细程度。

我特别想了解该功能
c
这样我就可以绘图了

pyplot.plot(xaxis, yaxis)
pyplot.show()

回到

yaxis = norm.pdf(xaxis, 0, 0.5)

1	yaxis = norm.pdf(xaxis, 0, 0.5)

* 我知道 norm..pdf 为对应的 x 值生成正态分布的成对 y 值。否则，如果 y 值无序，您将得到一个锯齿状的 x-y 图。
* 参数 0 和 0.5 是什么意思，我以为它们是均值和标准差，但是

>>> np.mean(y)
	     
0.16666666633781846

>>> np.std(y)
	     
0.25739817324489317

>>> np.mean(y)

0.16666666633781846

>>> np.std(y)

0.25739817324489317

我找不到合适的例子来解释这些参数，甚至https://docs.scipy.org.cn/doc/scipy/reference/generated/scipy.stats.norm.html也很模糊。

谢谢你，
来自令人兴奋的Belfield的Anthony

Jason Brownlee 2018 年 5 月 5 日上午 6:17 #

我们正在生成一个均值为 0、标准差为 1 的高斯数样本。这些数字按 x 轴排序。

这是一个函数，将 x 作为输入，y 作为输出。y 的线图显示了钟形。

安东尼考拉 2018 年 5 月 5 日上午 11:19 #

尊敬的Jason博士，
我同意你的看法，它应该生成均值为 0，标准差为 1。
但是当我这样做时

>>> np.mean(y)
	     
0.16666666633781846 ; # DEFINITELY NOT ZERO MEAN

>>> np.std(y)
	     
0.25739817324489317 # DEFINITELY NOT STD DEV of 1

>>> np.mean(y)

0.16666666633781846 ; # 绝对不是零均值

>>> np.std(y)

0.25739817324489317 # 绝对不是标准差为 1

总之，当我从均值为 0、标准差为 0.5 的正态分布生成序列 yaxis 时，我没有得到 0 和 0.5，而是 0.166 和 0.257。

换句话说，如果我生成函数

yaxis = norm.pdf(xaxis, 0, 0.5)

1	yaxis = norm.pdf(xaxis, 0, 0.5)

为什么我没有得到接近 0 或接近 0.5 的结果？

谢谢你
贝尔菲尔德的安东尼

Jason Brownlee 2018 年 5 月 6 日上午 6:21 #

我的错误，pdf() 的参数是“loc”和“scale”
https://docs.scipy.org.cn/doc/scipy/reference/generated/scipy.stats.norm.html

安东尼考拉 2018 年 5 月 6 日上午 7:16 #

尊敬的Jason博士，
当我查看 scipy.org 上上述超链接文档时，我不理解“loc”和“scale”的含义和应用

总而言之：“loc”和“scale”的含义以及如何从均值为 0、标准差为 1 的正态分布生成 pdf 或序列。

谢谢你，
新南威尔士州的安东尼

安东尼考拉 2018 年 5 月 8 日上午 8:09 #

尊敬的Jason博士，
scipy.org 页面 https://docs.scipy.org.cn/doc/scipy/reference/generated/scipy.stats.norm.html 的第一段说 loc = 均值，scale = 标准差。不知道为什么“他们”不能将参数称为均值和标准差。这应该是一致的。好的，我可以理解并为我的疏忽道歉。

但是，基于副标题“方差”的以下代码与 norm.pdf(x, loc, scale) 函数下的期望结果不符。

import numpy as np
from numpy import arange
from matplotlib import pyplot
from scipy.stats import norm
#
#
#generate the x value 
x_axis = arange(-3,3,0.001)

#generate the y value, based on line 10
#generate y value with mean =0, stddev = 1
y_axis = norm.pdf(x_axis,0,1)

#what the mean & stddev of the yaxis


np.mean(y_axis)
0.16621670028682048;#WHY NOT ZERO ACCORDING TO PDF? 

np.std(y_axis)
0.13923637660149782;#WHY NOT 1 ACCORDING TO PDFR?

import numpy as np

from numpy import arange

from matplotlib import pyplot

from scipy.stats import norm

#生成 x 值

x_axis = arange(-3,3,0.001)

#生成 y 值，基于第 10 行

#生成均值 = 0，标准差 = 1 的 y 值

y_axis = norm.pdf(x_axis,0,1)

# y 轴的均值和标准差是多少

np.mean(y_axis)

0.16621670028682048;#为什么不为零？

np.std(y_axis)

0.13923637660149782;#为什么不为 1？

再次，如果 norm.pdf 函数中的 loc 和 scale 分别为 0 和 1，为什么我得到的均值和标准差分别为 0.1622 和 0.1392。我希望我的 x_axis 长度为 6000 时，得到 0 和 1。

我以为生成一个 6000 个数字的序列应该能得到一个接近均值为 0、标准差为 1 的正态分布。我似乎遗漏了什么。

那是什么？

谢谢你，
新南威尔士州的安东尼

Jason Brownlee 2018 年 5 月 8 日下午 2:51 #

该函数不是生成高斯随机数，而是生成标准正态分布上提供的输入值的概率。

概率的分布不会具有均值为 0 和标准差为 1。

这有帮助吗？

以下是有关 PDF 的更多信息
https://en.wikipedia.org/wiki/Probability_density_function

安东尼考拉 2018 年 5 月 9 日晚上 9:45 #

尊敬的Jason博士，
感谢您引导我阅读 https://en.wikipedia.org/wiki/Probability_density_function 上关于 pdf 的文章。我突然想起了大学里使用 z 表的入门统计课程。您可以计算两个值之间事件的概率。

看过维基百科页面右侧的 pdf 后，所有关于曲线下面积在 +-1 标准差（x 轴）之间是 68.27%，在 +- 2 标准差（x 轴）之间是 95%，在 +- 3 标准差之间是 99% 的信息。

完全理解。

回到示例，我想计算函数在 -1 和 1 之间的概率。我期望得到 0.6827。相反，我得到了 682.7。

import numpy as np
from numpy import arange
from matplotlib import pyplot
from scipy.stats import norm
#
#
#generate the x value 
x_axis = arange(-3,3,0.001)
 
#generate the y value, based on line 10
#generate y value with mean =0, stddev = 1
y_axis = norm.pdf(x_axis,0,1)


#Select those values of x_axis between -1 and 1 and thus itscorresponding #values of the pdf

selected_values = y_axis[(x_axis >= -1 ) & (x_axis <= 1)]

#calculate the probability as the sum of the selected values, 
# Reference wiki article subheading "Absolutely continuous univariate 
# distributions

print(np.sum(selected_values))
682.6894518086525

import numpy as np

from numpy import arange

from matplotlib import pyplot

from scipy.stats import norm

#生成 x 值

x_axis = arange(-3,3,0.001)

#生成 y 值，基于第 10 行

#生成均值 = 0，标准差 = 1 的 y 值

y_axis = norm.pdf(x_axis,0,1)

#选择 x_axis 中介于 -1 和 1 之间的值及其对应的 #pdf 值

selected_values = y_axis[(x_axis >= -1 ) & (x_axis <= 1)]

#计算概率为所选值之和，

# 参考维基百科文章副标题“绝对连续单变量

# 分布

print(np.sum(selected_values))

682.6894518086525

总而言之：我明白您指的是 pdf。水平轴 = x_axis 代表标准差的数量。垂直轴是给定 x 值的概率。

但是为什么我得到 -1 和 1 标准差之间的 pdf 是 682.68945 而不是 0.68268945

谢谢你，
贝尔菲尔德的安东尼

安东尼考拉 2018 年 5 月 14 日下午 6:07 #

亲爱的 Jason 博士，

我已将相同的问题发布到此网站 https://oneau.wordpress.com/2011/02/28/simple-statistics-with-scipy/#comment-2276，并想分享答案。。

Prasanth 给出了答案。本质上，x 之间的距离是 0.001。所以你将每个对应的 f(x) 乘以 0.001，然后将 f(x) 相加。

所以这是正确的实现

import numpy as np
from numpy import arange
from matplotlib import pyplot
from scipy.stats import norm
#
#
#generate the x value 
x_axis = arange(-3,3,0.001)
 
#generate the y value, based on line 10
#generate y value with mean =0, stddev = 1
y_axis = norm.pdf(x_axis,0,1)
 
 
#Select those values of x_axis between -1 and 1 and thus itscorresponding #values of the pdf
#Note at the end of the line, multiply each f(x) by 0.001
 
selected_values = y_axis[(x_axis >= -1 ) & (x_axis <= 1)] * 0.001
 
#calculate the probability as the sum of the selected values, 
# Reference wiki article subheading "Absolutely continuous univariate 
# distributions
 
print(np.sum(selected_values))  #This is the total area under the curve
0.6826894518086525; #As expected

import numpy as np

from numpy import arange

from matplotlib import pyplot

from scipy.stats import norm

#生成 x 值

x_axis = arange(-3,3,0.001)

#生成 y 值，基于第 10 行

#生成均值 = 0，标准差 = 1 的 y 值

y_axis = norm.pdf(x_axis,0,1)

#选择 x_axis 中介于 -1 和 1 之间的值及其对应的 #pdf 值

#请注意，行尾将每个 f(x) 乘以 0.001

selected_values = y_axis[(x_axis >= -1 ) & (x_axis <= 1)] * 0.001

#计算概率为所选值之和，

# 参考维基百科文章副标题“绝对连续单变量

# 分布

print(np.sum(selected_values)) #这是曲线下的总面积

0.6826894518086525; #如预期

我知道这很简单，我会和大家分享，

此致，感谢
来自令人兴奋的悉尼的安东尼

Napoleon Boakye 2018 年 5 月 5 日上午 8:59 #

太棒了杰森！
一如既往；我带回家的最好部分是这个
“……报告模型分数高斯分布的两个参数和样本大小”

回复
- Jason Brownlee 2018 年 5 月 6 日上午 6:19 #
  
  谢谢，很高兴对您有帮助。
  
  回复
乔·斯托克斯 2020 年 3 月 20 日上午 11:04 #

如果我理解 numpy 文档正确，它默认输出总体标准差/方差。

您已经介绍了除以“N-1”的样本标准差/方差公式。

这是故意的吗？

回复
- Jason Brownlee 2020 年 3 月 20 日下午 1:18 #
  
  不，谢谢您的提醒。
  
  回复

导航

计算正态汇总统计量的温和介绍

教程概述

需要机器学习统计学方面的帮助吗？

高斯分布

样本与总体

测试数据集

集中趋势

方差

描述高斯分布

扩展

进一步阅读

API

文章

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

21 条对《计算正态汇总统计量的温和介绍》的回复

发表回复点击此处取消回复。

导航

教程概述

需要机器学习统计学方面的帮助吗？

高斯分布

样本与总体

测试数据集

集中趋势

方差

描述高斯分布

扩展

进一步阅读

API

文章

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

21 条对《计算正态汇总统计量的温和介绍》的回复

发表回复 点击此处取消回复。

发表回复点击此处取消回复。