在统计学和机器学习中,我们经常对变量进行线性变换或映射。
一个例子是特征变量的线性缩放。我们自然会认为,缩放后的值的平均值与原始变量平均值的缩放值是相同的。这是有道理的。
不幸的是,当我们使用变量的非线性变换时,这种直觉就会失效,因为这种关系不再成立。要纠正这种直觉,就需要发现 Jensen 不等式,它提供了在函数分析、概率和统计学中使用的标准数学工具。
在本教程中,您将了解 Jensen 不等式。
完成本教程后,您将了解:
- 线性映射的直觉不适用于非线性函数。
- 凸函数对变量的均值总是大于变量的均值,这被称为 Jensen 不等式。
- 该不等式的一个常见应用是在时间间隔的财务收益进行平均时,比较算术平均值和几何平均值。
开始您的项目,阅读我的新书《机器学习概率》,其中包含分步教程和所有示例的Python 源代码文件。
让我们开始吧。
- 更新于2019年10月:修正了一个小排版错误(感谢 Andy)。

简述 Jensen 不等式
照片由 gérard 拍摄,部分权利保留。
教程概述
本教程分为五个部分;它们是:
- 线性映射的直觉
- 非线性映射的不等式
- 发展 Jensen 不等式的直觉
- 算术平均值和几何平均值示例
- 其他应用
线性映射的直觉
我们经常使用线性函数对观测值进行变换,称为线性映射。
常见的线性变换包括旋转、反射和缩放。
例如,我们可能会将一组观测值乘以一个恒定的比例因子来进行缩放。
然后,我们可以从实际值和变换后的值的两个方面来处理和思考观测值。这可能包括计算汇总统计数据,如总和或平均值。
在处理原始状态和变换状态下的观测值时,我们会认为变换后值的平均值与原始观测值平均值的变换是相同的。
我们可以用x表示观测值,f()表示变换函数,mean()表示计算平均值,简洁地表述为:
- mean(f(x)) == f(mean(x)),对于线性 f()
这里的直觉是正确的,我们可以通过一个简单的例子来证明它。
考虑一个简单的游戏,我们掷一个公平的骰子,得到一个介于1到6之间的数字。我们可能为每次掷骰子设置一个奖励,是骰子点数的0.5倍。例如,掷出3会得到3 * 0.5 或 1.5 的奖励。
这意味着掷出3会得到3 * 0.5 或 1.5 的奖励。
我们可以定义我们的奖励函数如下:
|
1 2 3 |
# 变换函数 def payoff(x): return x * 0.5 |
接下来,我们可以定义可能的骰子点数范围以及每个值的变换。
|
1 2 3 4 |
# 骰子可能出现的点数 outcomes = [1, 2, 3, 4, 5, 6] # 每次掷骰子的奖励 payoffs = [payoff(value) for value in outcomes] |
接下来,我们可以计算奖励值的平均值,即变换后观测值的平均值。
|
1 2 3 |
# 结果的平均值(变换后的观测值平均值) v1 = mean(payoffs) print(v1) |
最后,我们可以比较平均掷骰子点的奖励,即平均观测值的变换。
|
1 2 3 |
# 平均结果的奖励(平均观测值的变换) v2 = payoff(mean(outcomes)) print(v2) |
我们期望这两个计算值始终相同。
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 比较平均线性变换与线性变换平均值的示例 from numpy import mean # 变换函数 def payoff(x): return x * 0.5 # 骰子可能出现的点数 outcomes = [1, 2, 3, 4, 5, 6] # 每次掷骰子的奖励 payoffs = [payoff(value) for value in outcomes] # 结果的平均值(变换后的观测值平均值) v1 = mean(payoffs) print(v1) # 平均结果的奖励(平均观测值的变换) v2 = payoff(mean(outcomes)) print(v2) |
运行该示例,可以计算出两个平均值(即线性奖励的平均值和平均值的线性奖励),并确认它们在我们示例中确实是等效的。
|
1 2 |
1.75 1.75 |
问题在于,当变换函数为非线性时,这种直觉不再适用。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
非线性映射的不等式
非线性函数是指输入和输出之间的关系不成一条直线。
相反,这种关系是弯曲的,例如向上弯曲,称为凸函数,或者向下弯曲,称为凹函数。我们可以通过反转函数的输出轻松地将凹函数转换为凸函数,因此我们通常讨论增长速度超过线性的凸函数。
例如,将输入平方的变换或 f(x) == x^2 是一个二次凸函数。这是因为随着 x 的增加,变换函数 f() 的输出随着输入的平方而增加。
我们关于变换后观测值的平均值与平均观测值的变换相同的直觉,对于凸函数不成立。
相反,如果变换函数是凸函数且观测值不恒定,则变换后观测值的平均值 mean(f(x)) 总是大于平均观测值的变换 f(mean(x))。我们可以将其表述为:
- mean(f(x)) >= f(mean(x)),对于凸函数 f() 且 x 不为常数
这个数学规则最早由Johan Jensen描述,并通常称为Jensen 不等式。
自然地,如果变换函数是凹函数,则大于号(>)变为小于号(<),如下所示:
- mean(f(x)) <= f(mean(x)),对于凹函数 f()
这起初并不直观,但有有趣的含义。
发展 Jensen 不等式的直觉
我们可以通过一个实际的例子来帮助理解 Jensen 不等式。
我们可以将掷骰子和线性奖励函数的例子更新为非线性奖励。
在这种情况下,我们可以使用 x^2 凸函数来奖励每次掷骰子的结果。例如,掷骰子得到3的奖励是3^2或9。更新的payoff()函数如下所示。
|
1 2 3 |
# 变换函数 def payoff(x): return x**2 |
我们可以计算每次掷骰子的奖励,并将结果绘制成点图,显示点数与奖励的关系。
这将为我们提供所有可能结果的非线性或凸奖励函数的直观理解。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 凸奖励函数的图 from matplotlib import pyplot # 变换函数 def payoff(x): return x**2 # 骰子可能出现的点数 outcomes = [1, 2, 3, 4, 5, 6] # 每次掷骰子的奖励 payoffs = [payoff(value) for value in outcomes] # 绘制凸奖励函数 pyplot.plot(outcomes, payoffs, label='convex') pyplot.legend() pyplot.show() |
运行示例,计算每次掷骰子的奖励,并绘制掷骰子点数与奖励的关系图。
图表显示了所有可能结果的奖励函数的凸形状。
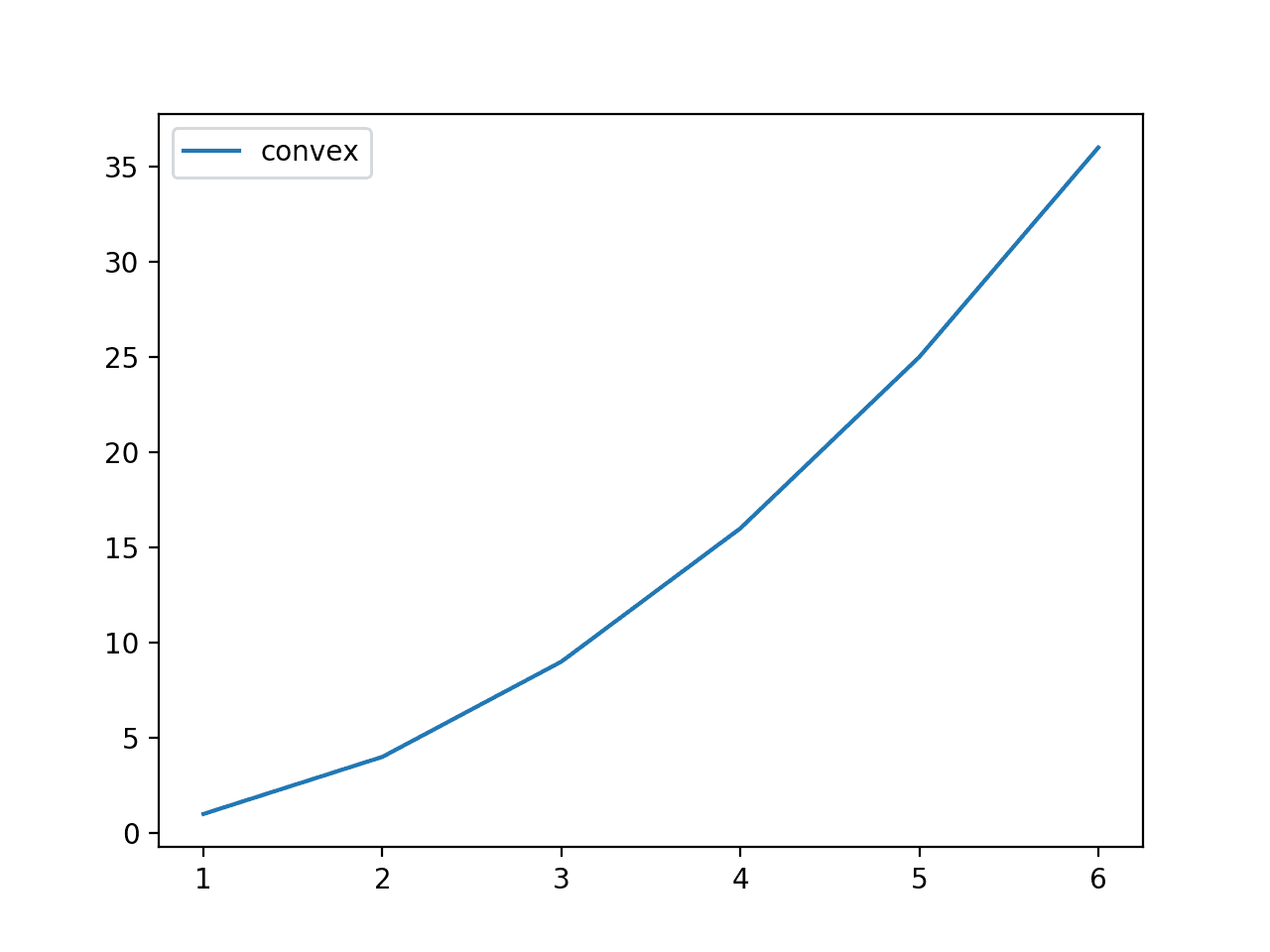
掷骰子点数与凸奖励函数的关系图
Jensen 不等式表明,奖励的平均值总是大于或等于平均结果的奖励。回顾一下,可能结果的范围是 [1,2,3,4,5,6],平均结果是3.5,因此我们知道平均结果的奖励是 3.5^2 或 12.25。我们的直觉让我们认为奖励的平均值也将接近 12.25,但这种直觉是错误的。
回顾一下,可能结果的范围是 [1,2,3,4,5,6],平均结果是3.5,因此我们知道平均结果的奖励是 3.5^2 或 12.25。我们的直觉让我们认为奖励的平均值也将接近 12.25,但这种直觉是错误的。
为了确认我们的直觉是错误的,让我们比较这两个值在所有可能结果上的表现。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 比较平均凸变换与凸变换平均值的示例 from numpy import mean # 变换函数 def payoff(x): return x**2 # 骰子可能出现的点数 outcomes = [1, 2, 3, 4, 5, 6] # 每次掷骰子的奖励 payoffs = [payoff(value) for value in outcomes] # 结果的平均值(变换后的观测值平均值) v1 = mean(payoffs) print(v1) # 平均结果的奖励(平均观测值的变换) v2 = payoff(mean(outcomes)) print(v2) |
运行示例,我们可以看到我们对平均结果奖励的直觉是正确的;该值为 12.25,正如我们所预期的。
我们可以看到直觉失效了,平均奖励值略高于 12.25。
回顾一下,平均值(算术平均值)实际上只是值的总和,然后除以值的数量。现在考虑一下,在奖励的情况下,我们正在对大得多的值进行求和,特别是 [1, 4, 9, 16, 25, 36],总和为 91。这会拉高我们的平均值。
直觉是,由于函数是凸的,变换后的值平均而言将总是大于原始结果值,或者任何其他我们想使用的求和类型操作。
|
1 2 |
15.166666666666666 12.25 |
还有一步可能有助于理解直觉,那就是采样。
我们已经看过了一个计算所有可能结果奖励的例子,但这并不常见。相反,我们更有可能从一个域中采样多个结果并计算每个结果的奖励。
我们可以通过多次掷骰子(例如50次)来实现这一点,计算每个结果的奖励,然后将平均奖励与平均结果的奖励进行比较。
|
1 2 3 |
... # 多次掷骰子 [1,6](例如50次) outcomes = randint(1, 7, 50) |
直观地说,我们期望平均结果接近理想值 3.5,因此平均值的奖励接近 3^2 或 12.25。我们也期望奖励值的平均值接近 15.1。
随机性允许许多重复的结果和每个结果的重要分布,因此奖励的平均值和平均值的奖励在每次实验重复时都会有所不同。我们将重复实验10次。每次重复,我们都期望不等式成立。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 重复 Jensen 不等式试验的示例 from numpy.random import randint from numpy import mean # 变换函数 def payoff(x): return x**2 # 重复试验 n_trials = 10 n_samples = 50 for i in range(n_trials): # 多次掷骰子 [1,6](例如50次) outcomes = randint(1, 7, n_samples) # 计算每个结果的奖励 payoffs = [payoff(x) for x in outcomes] # 计算奖励的平均值 v1 = mean(payoffs) # 计算平均结果的奖励 v2 = payoff(mean(outcomes)) # 确认预期 assert v1 >= v2 # 总结结果 print('>%d: %.2f >= %.2f' % (i, v1, v2)) |
运行示例,我们可以看到两个平均值在试验中发生了很大的变化。
注意:由于实验的随机性,您的具体结果可能会有所不同。
例如,我们看到平均奖励值低至 12.20,高至 16.88。我们看到平均结果的奖励值低至 9.36,高至 14.29。
然而,对于任何单次实验,Jensen 不等式都成立。
|
1 2 3 4 5 6 7 8 9 10 |
>0: 12.20 >= 9.73 >1: 14.14 >= 10.37 >2: 16.88 >= 13.84 >3: 15.68 >= 12.39 >4: 13.92 >= 11.56 >5: 15.44 >= 12.39 >6: 15.62 >= 13.10 >7: 17.50 >= 14.29 >8: 12.38 >= 9.36 >9: 15.52 >= 12.39 |
现在我们对 Jensen 不等式有了一些直观理解,让我们来看一些它被使用的例子。
算术平均值和几何平均值示例
Jensen 不等式的一个常见应用是比较算术平均值(AM)和几何平均值(GM)。
回顾一下,算术平均值是观测值的总和除以观测值的数量,并且仅当所有观测值具有相同的尺度时才适用。
例如
- (10 + 20) / 2 = 15
当样本观测值具有不同的尺度时,例如,指代不同的事物,那么就会使用几何平均值。
这包括首先计算观测值的乘积,然后取结果的n次方根,其中 n 是值的数量。对于两个值,我们使用平方根,对于三个值,我们使用立方根,依此类推。
例如
- sqrt(10 * 20) = 14.14
n次方根也可以使用 1/n 的指数来计算,从而使表示法和计算更简单。因此,我们的几何平均值可以计算为:
- (10 * 20)^(1/2) = 14.14
样本值将是我们的结果,n次方根将是我们的奖励函数,而n次方根是凹函数。
有关算术平均值和几何平均值之间差别的更多信息,请参阅:
乍一看,可能并不清楚这两个函数是如何关联的,但事实上,算术平均值也使用了 n=1 的 n次方根奖励函数,这没有任何影响。
回顾一下,n次方根和对数是彼此的逆函数。如果我们首先使用 n次方根或对数的逆作为奖励函数 f(),可以更清楚地建立它们之间的关系。
在几何平均值,或 GM 的情况下,我们计算的是对数结果的平均值:
- GM = mean( log(outcome) )
在算术平均值或 AM 的情况下,我们计算的是平均结果的对数。
- AM = log( mean(outcome) )
对数函数是凹函数,因此根据我们对 Jensen 不等式的了解,我们知道:
- geometric mean(x) <= arithmetic mean(x)
描述 AM 和 GM 不等式的约定是将 AM 放在前面,因此,该不等式可以概括为:
- arithmetic mean(x) >= geometric mean(x)
或者
- AM >= GM
我们可以通过一个简单的实际例子来弄清楚这一点,使用我们的掷骰子游戏 [1-6] 和对数奖励函数。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 比较对数几何平均值和对数算术平均值的示例 from numpy import mean from numpy import log from matplotlib import pyplot # 变换函数 def payoff(x): return log(x) # 骰子可能出现的点数 outcomes = [1, 2, 3, 4, 5, 6] # 每次掷骰子的奖励 payoffs = [payoff(value) for value in outcomes] # 结果的平均值(对数 GM) gm = mean(payoffs) # 平均结果的奖励(对数 AM) am = payoff(mean(outcomes)) # 打印结果 print('Log AM %.2f >= Log GM %.2f' % (am, gm)) # 点图显示点数与奖励的关系 pyplot.plot(outcomes, payoffs) pyplot.show() |
运行示例,确认了我们关于对数算术平均值大于对数几何平均值的预期。
|
1 |
Log AM 1.25 >= Log GM 1.10 |
还创建了一个所有可能点数与奖励的点图,显示了 log() 函数的凹性。
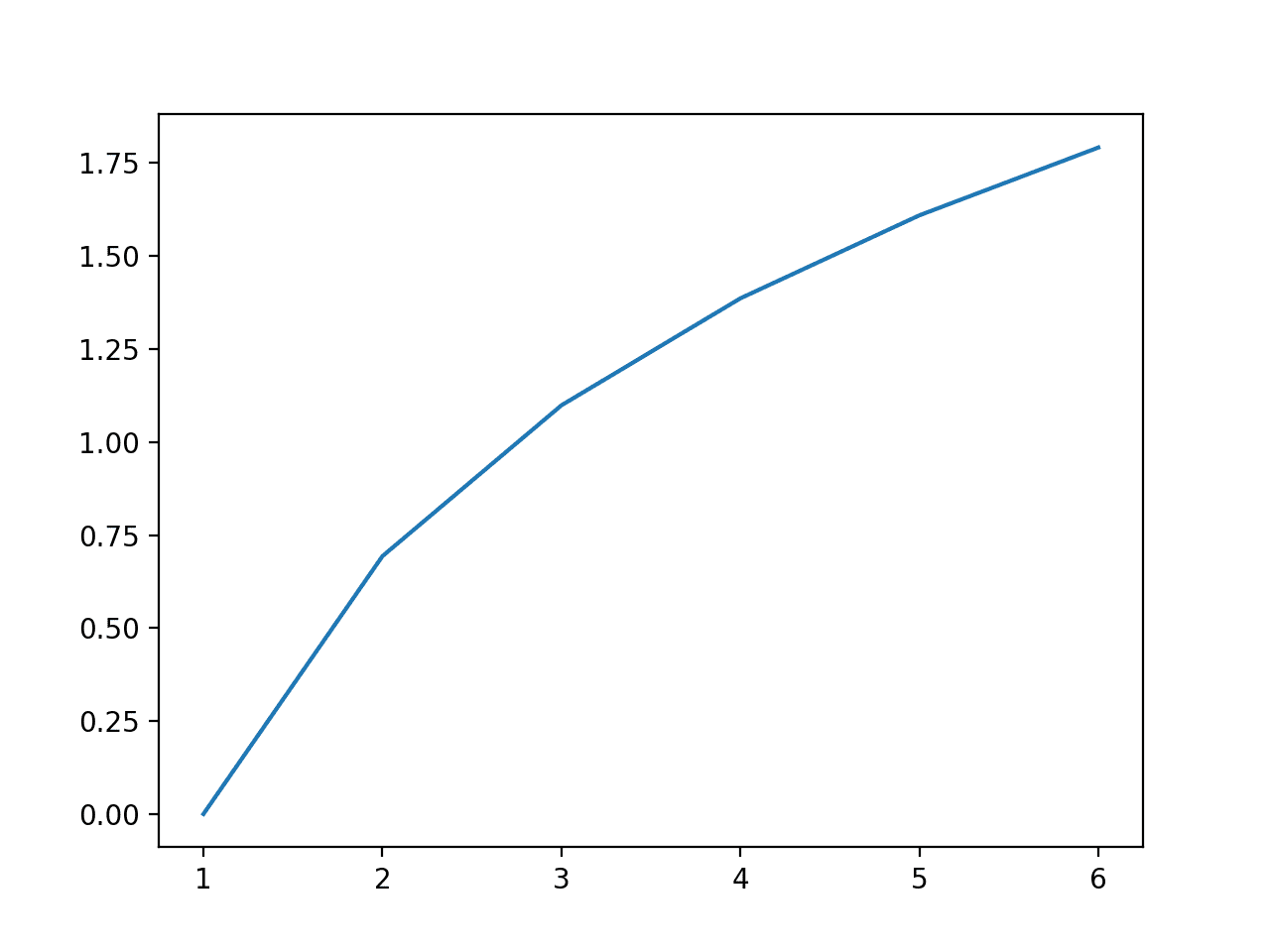
所有掷骰子点数与对数奖励函数的关系图,显示了凹函数
我们现在可以从两个平均值计算中移除对数。这可以通过对两边使用逆对数函数或 n次方根来轻松完成。
将对数移除并替换为几何平均值的 n次方根,即可得到正常的几何平均值计算:
- geometric mean = [1 * 2 * 3 * 4 * 5 * 6]^(1/6)
回顾一下,6次方根也可以通过指数 1/6 来计算。
算术平均值可以使用 1 次方根计算,这不会产生任何影响,即平均值加上指数 1/1 或乘以 1 次方,因此算术平均值为:
- arithmetic = [1 + 2 + 3 + 4 + 5 + 6]/6
平方根函数与对数函数一样是凹函数,Jensen 不等式仍然成立。
- arithmetic mean(x) >= geometric mean(x)
这被称为算术平均值和几何平均值不等式,或简称AM-GM 不等式。
该不等式在处理金融时间序列时很重要,例如计算回报率。
例如,年化平均回报率可以在一个区间(如每月)上计算。可以使用算术平均值来计算,但该值会偏高(一个较大的值),并且会忽略回报的再投资,并假设任何损失将在每个时期开始时得到弥补。
相反,必须使用几何平均值来给出区间内的真实平均回报率(一个较小的值),它正确地考虑了再投资的损失和复利收益。
算术平均回报率总是高于几何平均回报率,在这种情况下具有误导性。
其他应用
Jensen 不等式是数学中的一个有用工具,特别是在概率和统计等应用领域。
例如,它经常作为数学证明的工具。
它还用于对一个函数做出声明,而对该函数的分布知之甚少或不需要了解。一个例子是该不等式在定义随机变量概率的下界时的应用。
Jensen 不等式还为 Nassim Taleb 2012 年的书《Antifragile》中“反脆弱”的概念提供了数学基础。上面描述的掷骰子凸奖励函数的例子受到该书(第19章)一节的启发。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 实数与复数分析, 1987.
- 不等式, 1988.
- 反脆弱:从混乱中获益的事物, 2012.
文章
总结
在本教程中,您了解了数学和统计学中的 Jensen 不等式。
具体来说,你学到了:
- 线性映射的直觉不适用于非线性函数。
- 凸函数对变量的均值总是大于变量的均值,这被称为 Jensen 不等式。
- 该不等式的一个常见应用是在时间间隔的财务收益进行平均时,比较算术平均值和几何平均值。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






这意味着掷出3会得到3 * 0.3 或 1.5 的奖励。(?)
在什么上下文中,Andy?
我猜这是一个拼写错误,应该是 3 * 0.5 或 1.5
谢谢,已修正。
干得好,谢谢。
一个小的修正
“f(x) == x^2 是一个指数凸函数。这是因为随着 x 的增加,变换函数 f() 的输出以指数速率增加。”
我们说 f() 是二次方增长而不是指数级增长,因为 x(我们的输入)不在指数中。
你说得很对,谢谢!
二次方是变量的值,指数是变量的指数。