不可否认,微积分是一门困难的学科。但是,如果你掌握了基础知识,不仅能够理解更复杂的概念,还会觉得它们很有趣。为了理解机器学习算法,你需要掌握诸如函数梯度、矩阵海森以及优化等概念。极限和连续性的概念是所有这些主题的基础。
在本帖中,你将了解如何求函数的极限,以及如何判断一个函数是否连续。
阅读本帖后,你将能够
- 确定函数 f(x) 在 x 趋近于某个值时是否存在极限
- 求函数 f(x) 在 x 趋近于 a 时的极限
- 确定函数在某一点或某个区间上是否连续
让我们开始吧。
教程概述
本教程分为两部分
- 极限
- 确定函数在某一点的极限是否存在
- 计算函数在某一点的极限
- 极限的正式定义
- 极限示例
- 左极限和右极限
- 连续性
- 连续性的定义
- 确定函数在某一点或某个区间上是否连续
- 连续函数示例
一个简单的例子
让我们从一个简单的函数 f(x) 开始,该函数由下式给出:
f(x) = 1+x
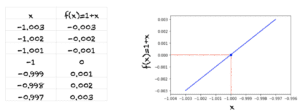
当 x 趋近于 -1 时,f(x) 会发生什么?
我们可以看到,当 x 从 x=-1 的两侧越来越接近 -1 时,f(x) 越来越接近 0。在 x=-1 时,函数恰好为零。我们说,当 x 趋近于 -1 时,f(x) 的极限为 0。
拓展示例
拓展问题。我们定义 g(x)
g(x) = (1-x^2)/(1+x)
我们可以将 g(x) 的表达式简化为:
g(x) = (1-x)(1+x)/(1+x)
如果分母不为零,则 g(x) 可以简化为:
g(x) = 1-x, 如果 x ≠ -1
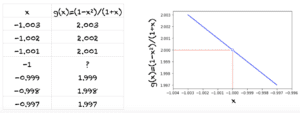
然而,在 (x = -1) 时,分母为零,我们不能除以零。因此,看起来函数在 x=-1 处有一个“洞”。尽管存在这个“洞”,但正如图中所示,当 x 越来越接近 -1 时,g(x) 越来越接近 2。
这就是极限的基本思想。如果 g(x) 在一个不包含 -1 的开区间内定义,并且当 x 趋近于 -1 时 g(x) 越来越接近 2,我们就将其写为:
lim(x→-1) g(x) = 2
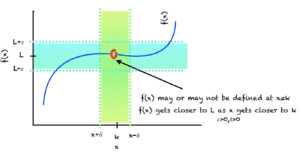
一般来说,对于任何函数 f(x),如果当 x 越来越接近 k 时,f(x) 越来越接近一个值 L,我们就将 f(x) 在 x 趋近于 k 时的极限定义为 L。这可以写为:![]()
左极限和右极限
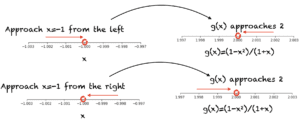
对于函数 g(x),无论我们是增加 x 来接近 -1(从左边趋近 -1)还是减小 x 来接近 -1(从右边趋近 -1),g(x) 都越来越接近 2。下图展示了这一点。
这就产生了单侧极限的概念。左极限定义在 -1 左侧的一个不包含 -1 的区间上,例如 (-1.003, -1)。当我们从左侧趋近 -1 时,g(x) 越来越接近 2。
类似地,右极限定义在 -1 右侧的一个开区间上,并且不包含 -1,例如 (-1, 0.997)。当我们从右侧趋近 -1 时,g(x) 的右极限是 2。左极限和右极限都可以写成如下形式:
如果我们说 f(x) 在 x 趋近于 k 时的极限为 L,当且仅当其左极限和右极限都相等。因此,这是检验函数在特定点是否具有极限的另一种方法,即: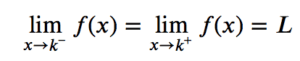
极限的正式定义
在数学中,我们需要对所有事物都有一个精确的定义。为了正式定义极限,我们将使用希腊字母 epsilon 的概念。数学界同意使用 epsilon 表示任意小的正数,这意味着我们可以让 epsilon 任意小,并且它尽可能接近零,前提是 epsilon>0(所以 epsilon 不能为零)。
当 x 趋近于 k 时,f(x) 的极限为 L,如果对于每一个 epsilon>0,都存在一个正数 delta>0,使得
如果 0<|x−k|<delta,则 |f(x)−L|<epsilon
这个定义非常直接。x-k 是 x 与 k 的差值,而 |x-k| 是 x 与 k 的距离,它忽略了差值的符号。类似地,|f(x)-L| 是 f(x) 与 L 的距离。因此,定义说明,当 x 与 k 的距离趋近于一个任意小的值时,f(x) 与 L 的距离也趋近于一个非常小的值。下图很好地说明了上述定义。
极限示例
下图说明了一些示例,并在下方进行了解释。
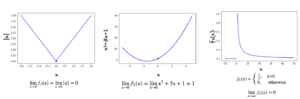
1.1 绝对值示例
f_1(x) = |x|
f_1(x) 在所有 x 值处都有极限,例如,lim(x→0) f_1(x) = 0。
1.2 多项式示例
f_2(x) = x^2 + 3x + 1
f_2(x) 在所有 x 值处都有极限,例如,lim(x→1) f_2(x) = 1+3+1 = 5。
1.3 无穷大示例
f_3(x) = 1/x, 如果 x>0
f_3(x) = 0, 如果 x<=0
对于上述情况,当 x 越来越大时,f_3(x) 的值越来越小,趋近于零。因此,lim(x→∞) f_3(x) = 0。
没有极限的函数示例
从极限的定义可以看出,以下函数没有极限:
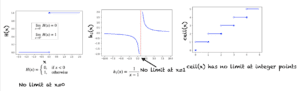
2.1 单位阶跃函数
单位阶跃函数 H(x) 由下式给出:
H(x) = 0, 如果 x<0
H(x) = 1, 否则
当 x 从左侧趋近于 0 时,函数保持为零。但是,一旦我们到达 x=0,H(x) 就跃升到 1,因此 H(x) 在 x 趋近于零时没有极限。该函数在 x 趋近于零时有一个等于零的左极限和一个等于一的右极限。
当 x→0 时,左极限和右极限不相等,因此 H(x) 在 x 趋近于 0 时没有极限。这里,我们使用了左极限和右极限相等作为检验函数在特定点是否有极限的方法。
2.2 倒数函数
考虑 h_1(x)
h_1(x) = 1/(x-1)
当我们从左侧趋近 x=1 时,函数趋向于大的负值。当我们从右侧趋近 x=1 时,h_1(x) 增加到大的正值。因此,当 x 接近 1 时,h_1(x) 的值不会接近一个固定的实数值。因此,x→1 的极限不存在。
2.3 向上取整函数
考虑向上取整函数,它将一个具有非零小数部分的实数四舍五入到下一个整数值。因此,lim(x→1) ceil(x) 不存在。事实上,ceil(x) 在任何整数值处都没有极限。
以上所有示例均在下图所示。
连续性
如果您理解了极限的概念,那么理解连续性就很简单了。如果函数在某一点 a 处连续,则满足以下三个条件:
- f(a) 必须存在
- f(x) 在 x 趋近于 a 时存在极限
- f(x) 在 x 趋近于 a 时的极限等于 f(a)
如果以上所有条件都成立,则函数在点 a 处是连续的。以下是一些示例:
连续性示例
连续性的概念与极限密切相关。如果函数在某一点有定义,在该点没有跳跃,并且在该点存在极限,那么它在该点是连续的。下图显示了一些示例,并在下方进行了解释。
3.1 平方函数
以下函数 f_4(x) 在所有 x 值处都是连续的:
f_4(x) = x^2
3.2 有理函数
我们之前使用的函数 g(x)
g(x) = (1-x^2)/(1+x)
g(x) 在 x=-1 处除外,处处连续。
我们可以修改 g(x) 为 g*(x):
g*(x) = (1-x^2)/(1+x),如果 x ≠ -1
g*(x) = 2,否则
现在我们得到了一个在所有 x 值处都连续的函数。
3.3 倒数函数
回到我们之前的 f_3(x) 示例:
f_3(x) = 1/x, 如果 x>0
f_3(x) = 0, 如果 x<=0
f_3(x) 在 x=0 处除外,处处连续,因为 f_3(x) 的值在 x=0 处有一个很大的跳跃。因此,在 x=0 处存在不连续性。
进一步阅读
如果您想深入了解该主题,本节提供了更多资源。数学在于实践,以下是一些将提供更多关于此主题的练习和示例的资源列表。
资源页面
- Jason Brownlee 的优秀资源,关于机器学习微积分书籍。
书籍
- Thomas’ Calculus,第 14 版,2017 年。(基于 George B. Thomas 的原作,由 Joel Hass、Christopher Heil、Maurice Weir 修订)。
- Calculus,第 3 版,2017 年。(Gilbert Strang)。
- Calculus,第 8 版,2015 年。(James Stewart)。
总结
在本帖中,您学习了极限和连续性的微积分概念。
具体来说,你学到了:
- 函数在趋近某一点时是否存在极限
- 函数在某一点或某个区间内是否连续
您有任何问题吗?请在下方评论区提问,我将尽力回答。









恭喜您发布了这篇帖子!
我想知道这些概念在实际机器学习算法中是如何应用的?您能帮我吗?
此致!
请参阅引言:“为了理解机器学习算法,你需要掌握诸如函数梯度、矩阵海森以及优化等概念。极限和连续性的概念是所有这些主题的基础。”