多头潜在注意力（Multi-Head Latent Attention, MLA）简明介绍

作者： Adrian Tam 发布于 2025年8月18日在构建Transformer模型 0

并非所有Transformer模型都称为“大型语言模型”，因为您可以使用Transformer架构构建一个非常小的模型。真正大型的Transformer模型通常在家里使用不切实际，因为它们太大无法容纳在一台计算机上，而且如果没有GPU集群，运行速度也会太慢。

最近引入的多头潜在注意力（Multi-Head Latent Attention，MLA）提出了一种以更低内存占用运行注意力操作的新方法。它最初在DeepSeek-V2中提出，改变了您在注意力操作中执行矩阵乘法的方式。在这篇文章中，您将学习MLA的工作原理以及如何在PyTorch中实现它。

让我们开始吧。

多头潜在注意力（Multi-Head Latent Attention, MLA）简明介绍
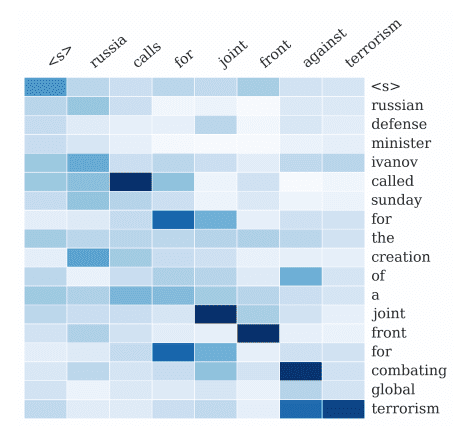
图片来源：Victoriano Izquierdo。保留部分权利。

概述

这篇博文分为三部分；它们是：

矩阵的低秩近似
多头潜在注意力 (MLA)
PyTorch实现

矩阵的低秩近似

多头注意力（MHA）和分组查询注意力（GQA）是几乎所有Transformer模型中使用的注意力机制。最近，DeepSeek-V2提出了一种名为多头潜在注意力（MLA）的新注意力机制，以进一步降低计算成本并加快推理速度。

其核心思想是使用低秩近似将一个大矩阵转换为两个小矩阵，$M\approx UV$。如果矩阵$M$是一个$n\times m$矩阵，$U$将是一个$n\times r$矩阵，$V$将是一个$r\times m$矩阵，其中$r$小于$n$和$m$。乘积$UV$不会与$M$完全相同，但对于实际应用来说已经足够接近。将$M$分解为$U$和$V$的一种方法是使用奇异值分解（SVD）并选择前$r$个正交基。具体来说，矩阵$M$的SVD产生

$$
M = U \Sigma V^T
$$

其中$U$和$V$是方阵（正交基），$\Sigma$是对角矩阵，包含$M$的奇异值。如果您将$\Sigma$对角线上的较低奇异值归零，您实际上就删除了$U$和$V$的较低行。此乘法的结果是$M$的近似值。如果从$\Sigma$中归零的元素在数值上接近于零，则此近似值将非常准确。

这个概念并不新鲜。低秩适应是微调大型Transformer模型的常用技术，它也使用这种投影矩阵的近似来增强模型以实现新功能。

多头潜在注意力 (MLA)

与GQA只操作键和值投影类似，多头潜在注意力（MLA）也只分解键和值投影。然而，与GQA不同的是，MLA不跨多个查询共享键和值投影，而是以与多头注意力相同的方式操作。原始论文将MLA描述为在推理过程中在键/值空间的压缩潜在表示上操作。

对于输入序列$X$，使用MLA的自注意力计算为

$$
\begin{aligned}
Q &= XW_Q^DW_Q^U = (XW_Q^D)W_Q^U = C_QW_Q^U \\
K &= XW_{KV}^DW_K^U = (XW_{KV}^D)W_K^U = C_{KV}W_K^U \\
V &= XW_{KV}^DW_V^U = (XW_{KV}^D)W_V^U = C_{KV}W_V^U
\end{aligned}
$$

其中

$W_Q^D,W_{KV}^D \in \mathbb{R}^{d\times r}$ 是低秩压缩矩阵，具有较小的$r$，用于降低维度。
$W_Q^U,W_K^U,W_V^U \in \mathbb{R}^{r\times(n_h d_h)}$ 是解压缩矩阵，用于恢复维度。
$r$ 是潜在维度，通常 $r \ll n_h\cdot d_h$。

您可能会注意到，例如$K$是通过两次矩阵乘法而不是一次从$X$投影计算出来的。这看起来可能浪费计算，但在下面的解释中您会看到这实际上是高效的。

现在考虑标准注意力操作

$$
\begin{aligned}
O_i &= \text{softmax}\big(\frac{QK^\top}{\sqrt{d_k}}\big)V \\
&= \text{softmax}\big(\frac{(XW_Q^D W_{Q,i}^U)(XW_{KV}^D W_{K,i}^U)^\top}{\sqrt{d_k}}\big)XW_{KV}^D W_V^U \\
&= \text{softmax}\big(\frac{XW_Q^D W_{Q,i}^U {W_{K,i}^U}^\top {W_{KV}^D}^\top X^\top}{\sqrt{d_k}}\big)XW_{KV}^D W_{V,i}^U \\
&= \text{softmax}\big(\frac{C_Q W_{Q,i}^U {W_{K,i}^U}^\top C_{KV}^\top}{\sqrt{d_k}}\big)C_{KV} W_{V,i}^U
\end{aligned}
$$

这就是MLA计算节省的来源：它没有独立地分解键和值投影矩阵$W^K$和$W^V$，而是共享压缩矩阵。回想一下，即使在交叉注意力中，键和值输入序列也是相同的，因此您为$K$和$V$投影共享一个因子$C_{KV}$。

另一个关键技术是，多头注意力仅在解压缩矩阵 $W_Q^U, W_K^U, W_V^U$ 中实现。因此，对于单个头，上述方程使用符号 $W_{Q,i}^U, W_{K,i}^U, W_{V,i}^U$。通过这种方式，$C_Q$ 和 $C_{KV}$ 只计算一次，并由所有头共享。

此外，请注意上述softmax最后一行中的矩阵乘法$W_{Q,i}^U{W_{K,i}^U}^\top$。这是两个解压缩矩阵的乘法，与输入$X$无关。因此，这个矩阵乘法可以预先计算并缓存为$W_{QK,i} = W_{Q,i}^U{W_{K,i}^U}^\top$，从而节省推理时间。

通过分解投影矩阵并对潜在表示使用较低的维度，MLA即使涉及更多矩阵，也能节省计算和内存使用。

PyTorch实现

一旦您理解了 MLA 的设计，在 PyTorch 中实现它就非常简单了。以下是一个示例：

import math
import torch
import torch.nn as nn

class MultiHeadLatentAttention(nn.Module):
    def __init__(self, d_model=128*128, num_heads=128, q_latent_dim=12, kv_latent_dim=4):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.q_latent_dim = q_latent_dim
        self.kv_latent_dim = kv_latent_dim
        head_dim = d_model // num_heads

        # Query projections
        self.Wq_d = nn.Linear(d_model, q_latent_dim)

        # Precomputed matrix multiplications of W_q^U and W_k^U, for multiple heads
        self.W_qk = nn.Linear(q_latent_dim, num_heads * kv_latent_dim)

        # Key/Value latent projections
        self.Wkv_d = nn.Linear(d_model, kv_latent_dim)
        self.Wv_u = nn.Linear(kv_latent_dim, num_heads * head_dim)

        # Output projection
        self.Wo = nn.Linear(num_heads * head_dim, d_model)

    def forward(self, x):
        batch_size, seq_len, d_model = x.shape

        # Projections of input into latent spaces
        C_q = self.Wq_d(x)     # shape: (batch_size, seq_len, q_latent_dim)
        C_kv = self.Wkv_d(x)   # shape: (batch_size, seq_len, kv_latent_dim)

        # Attention score, shape: (batch_size, num_heads, seq_len, seq_len)
        C_qW_qk = self.W_qk(C_q).view(batch_size, seq_len, self.num_heads, self.kv_latent_dim)
        scores = torch.matmul(C_qW_qk.transpose(1, 2), C_kv.transpose(-2, -1)[:, None, ...]) / math.sqrt(self.kv_latent_dim)

        # Attention computation
        attn_weight = torch.softmax(scores, dim=-1)
        # Restore V from latent space
        V = self.Wv_u(C_kv).view(batch_size, seq_len, self.num_heads, -1)
        # Compute attention output, shape: (batch_size, seq_len, num_heads, head_dim)
        output = torch.matmul(attn_weight, V.transpose(1,2)).transpose(1,2).contiguous()
        # Concatentate the heads, then apply output projection
        output = self.Wo(output.view(batch_size, seq_len, -1))
        return output

import math

import torch

import torch.nn as nn

class MultiHeadLatentAttention(nn.Module):

def __init__(self, d_model=128*128, num_heads=128, q_latent_dim=12, kv_latent_dim=4):

super().__init__()

self.d_model = d_model

self.num_heads = num_heads

self.q_latent_dim = q_latent_dim

self.kv_latent_dim = kv_latent_dim

head_dim = d_model // num_heads

# Query projections

self.Wq_d = nn.Linear(d_model, q_latent_dim)

# Precomputed matrix multiplications of W_q^U and W_k^U, for multiple heads

self.W_qk = nn.Linear(q_latent_dim, num_heads * kv_latent_dim)

# Key/Value latent projections

self.Wkv_d = nn.Linear(d_model, kv_latent_dim)

self.Wv_u = nn.Linear(kv_latent_dim, num_heads * head_dim)

# Output projection

self.Wo = nn.Linear(num_heads * head_dim, d_model)

def forward(self, x):

batch_size, seq_len, d_model = x.shape

# Projections of input into latent spaces

C_q = self.Wq_d(x) # shape: (batch_size, seq_len, q_latent_dim)

C_kv = self.Wkv_d(x) # shape: (batch_size, seq_len, kv_latent_dim)

# Attention score, shape: (batch_size, num_heads, seq_len, seq_len)

C_qW_qk = self.W_qk(C_q).view(batch_size, seq_len, self.num_heads, self.kv_latent_dim)

scores = torch.matmul(C_qW_qk.transpose(1, 2), C_kv.transpose(-2, -1)[:, None, ...]) / math.sqrt(self.kv_latent_dim)

# Attention computation

attn_weight = torch.softmax(scores, dim=-1)

# Restore V from latent space

V = self.Wv_u(C_kv).view(batch_size, seq_len, self.num_heads, -1)

# Compute attention output, shape: (batch_size, seq_len, num_heads, head_dim)

output = torch.matmul(attn_weight, V.transpose(1,2)).transpose(1,2).contiguous()

# Concatentate the heads, then apply output projection

output = self.Wo(output.view(batch_size, seq_len, -1))

return output

将这段代码与上一节中的方程式进行比较，您可以看到$W_{QK,i}$在此模块中直接定义为一个组件。

forward()方法的输入序列x的形状为(batch_size, seq_len, d_model)，最终输出也一样。首先，输入x被投影到C_q和C_kv中，它们由所有注意力头共享。接下来，使用两次矩阵乘法计算每个头的注意力分数。首先，您使用self.W_qk乘以C_q，然后将结果重塑为(batch_size, seq_len, num_heads, kv_latent_dim)。然后，在进行适当的轴转置后，将其与C_kv相乘，以获得注意力分数。由于C_qW_qk是一个4维张量，而C_kv是一个3维张量，因此您在C_kv中为num_heads维度添加了一个虚拟维度。