研究依赖于多个变量的函数通常是很有益的。
多元微积分通过将微积分中的概念(例如变化率的计算)扩展到多个变量,为我们提供了实现这一目标的工具。它在训练神经网络的过程中扮演着至关重要的角色,梯度被广泛用于更新模型参数。
在本教程中,您将发现多元微积分的温和入门。
完成本教程后,您将了解:
- 多元函数依赖于多个输入变量来产生一个输出。
- 多元函数的梯度是通过计算函数在不同方向上的导数来得到的。
- 多元微积分在神经网络中被广泛用于更新模型参数。
让我们开始吧。

多元微积分简明介绍
图片来源:Luca Bravo,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 重新审视函数概念
- 多元函数的导数
- 多元微积分在机器学习中的应用
重新审视函数概念
我们已经熟悉了函数的概念,它是一个定义因变量和自变量之间关系的规则。我们已经看到函数通常表示为 y = f(x),其中输入(或自变量)x 和输出(或因变量)y 都是单个实数。
这种接受单个自变量并定义输入和输出之间一对一映射的函数,称为*单变量*函数。
例如,假设我们试图仅根据温度预测天气。在这种情况下,天气是我们试图预测的因变量,它是作为输入变量的温度的函数。因此,这样的问题可以很容易地转化为一个单变量函数。
然而,假设我们现在除了温度之外,还想根据湿度水平和风速来预测天气。我们不能通过单变量函数来实现,因为其输出仅依赖于单个输入。
因此,我们将注意力转向*多元*函数,之所以这样称呼,是因为这些函数可以接受多个变量作为输入。
形式上,我们可以将多元函数表示为多个实数输入变量 n 到一个实数输出的映射
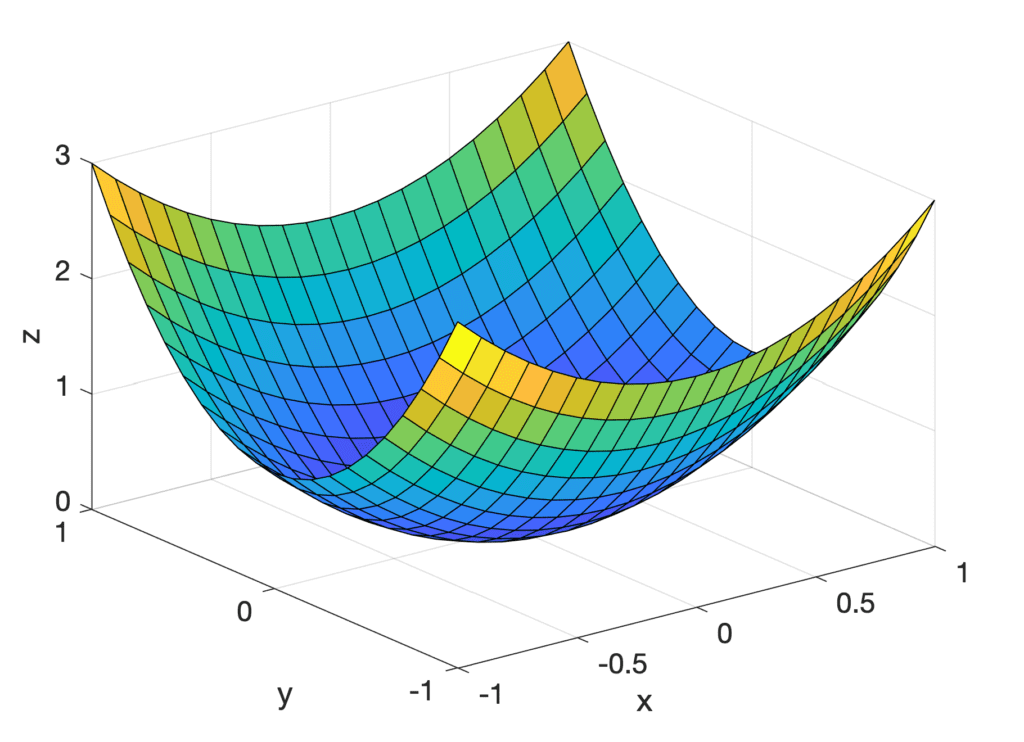
例如,考虑以下抛物面
f(x, y) = x2 + 2y2
这是一个多元函数,它接受两个变量 x 和 y 作为输入(因此 n = 2)来产生一个输出。我们可以通过绘制其在 x 和 y 介于 -1 和 1 之间的值来可视化它。
类似地,我们可以有接受更多变量作为输入的多元函数。然而,由于涉及的维度数量,可视化它们可能很困难。
我们甚至可以进一步推广函数的概念,考虑将多个输入 n 映射到多个输出 m 的函数
这些函数通常被称为*向量值*函数。
多元函数的导数
回想一下,微积分研究的是变化率。对于某个单变量函数 g(x),这可以通过计算其导数来实现
将导数推广到多个变量的函数就是梯度。
——《机器学习数学》,第146页,2020年。
求多元函数梯度的方法是每次只改变一个变量,同时保持其他变量不变。通过这种方式,我们将每次对我们的多元函数求相对于每个变量的*偏导数*。
梯度就是这些偏导数的集合。
——《机器学习数学》,第146页,2020年。
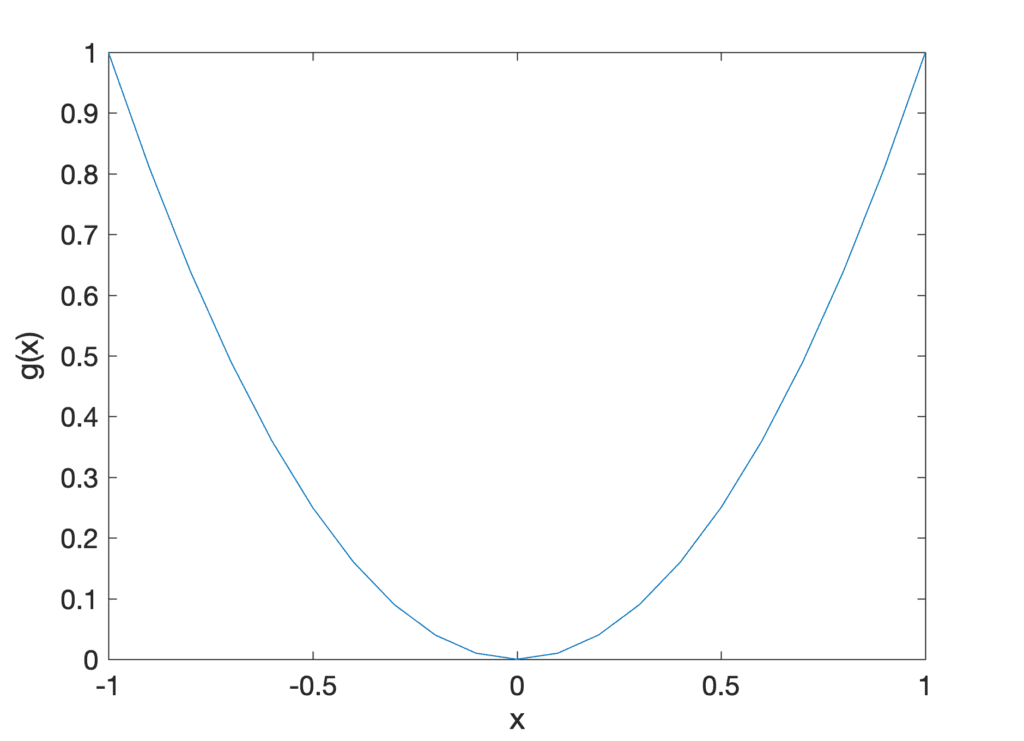
为了更好地可视化此技术,我们首先考虑一个简单的单变量二次函数,形式为
g(x) = x2
在某个点 x 处求此函数的导数需要应用我们之前定义的 g’(x) 的方程。我们也可以通过使用幂法则来简化,从而得到
g’(x) = 2x
此外,如果我们想象将前面讨论的抛物面用一个穿过 y = 0 的平面切开,我们会发现 f(x, y) 产生的横截面是二次曲线 g(x) = x2。因此,我们可以通过对 f(x, y) 求导并保持 y 不变,来计算抛物面在 x 方向上的导数(或陡度,或*斜率*)。我们将其称为 f(x, y) 对 x 的*偏*导数,并用 ∂ 表示,以表明除了 x 之外还有其他变量,但目前不予考虑。因此,f(x, y) 对 x 的偏导数为
我们也可以类似地保持 x 不变(或者换句话说,通过一个穿过常数 x 值的平面来切割抛物面以找到其横截面),从而找到 f(x, y) 对 y 的偏导数,如下所示
我们本质上所做的就是找到了 f(x, y) 在 x 和 y 方向上各自的单变量导数。将这两个单变量导数结合作为最后一步,就得到了多元导数(或梯度)
同样的技术也适用于高维函数。
多元微积分在机器学习中的应用
偏导数在神经网络中被广泛用于更新模型参数(或权重)。
我们已经看到,在最小化某个误差函数时,优化算法将试图沿着其梯度下坡。如果这个误差函数是单变量的,因此是单个独立权重的函数,那么优化它将只需计算其单变量导数。
然而,一个神经网络包含许多权重(每个权重归属于不同的神经元),误差是这些权重的函数。因此,更新权重值需要计算误差曲线相对于所有这些权重的梯度。
这就是多元微积分发挥作用的地方。
误差曲线的梯度是通过求误差对每个权重的偏导数来计算的;换句话说,通过保持所有权重不变,只考虑当前权重,来求误差函数的导数。这使得每个权重都可以独立于其他权重进行更新,从而达到找到一组最优权重的目标。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 单变量与多变量微积分, 2020.
- 机器学习数学, 2020.
- 优化算法, 2019.
- 深度学习, 2019.
总结
在本教程中,您了解了多元微积分的温和入门。
具体来说,你学到了:
- 多元函数依赖于多个输入变量来产生一个输出。
- 多元函数的梯度是通过计算函数在不同方向上的导数来得到的。
- 多元微积分在神经网络中被广泛用于更新模型参数。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
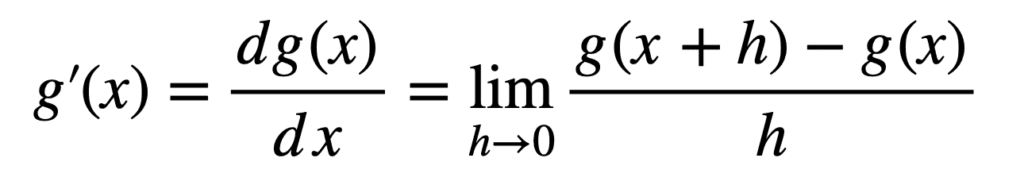
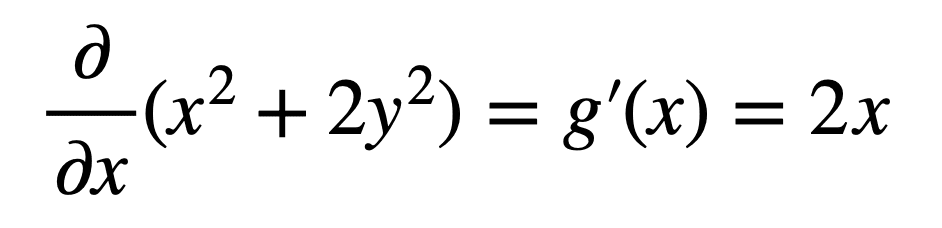
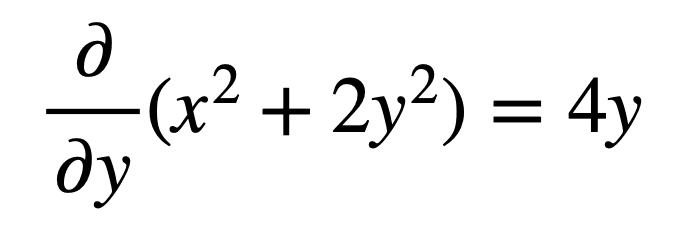
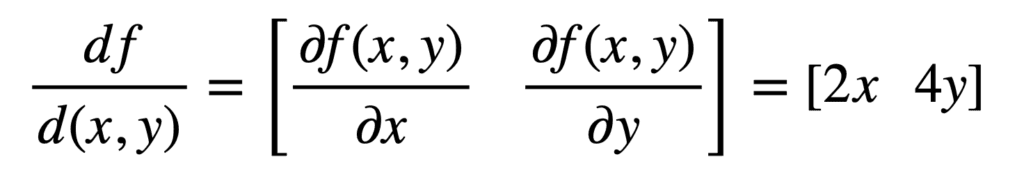




尊敬的 Stefania 博士
感谢您对多元微积分的出色讲解。解释得非常清楚,易于
理解。
致以最诚挚的问候
Jayaganthan
谢谢你,Jayaganthan。很高兴你觉得它有用。
关于微积分如何帮助人们掌握机器学习和人工智能的精彩介绍。
感谢您对许多人认为抽象的学科进行简单流畅的解释和叙述
谢谢你的好意,Meshack。
多元微积分的详细介绍和解释。非常感谢 Stefania。
谢谢您的评论!
你好 Stefania,
非常清楚,让我完全理解了梯度以及如何在机器学习中应用它。
谢谢你,Bruce!