Python 正态性检验简明入门

作者 Jason Brownlee 于 2019年8月8日发表在统计学 128

在处理数据样本时，一个重要的决策点是使用参数统计方法还是非参数统计方法。

参数统计方法假定数据具有已知且特定的分布，通常是高斯分布。如果数据样本不是高斯分布，那么参数统计检验的假设就会被违反，必须使用非参数统计方法。

存在一系列技术可以用来检查你的数据样本是否偏离高斯分布，这些技术被称为正态性检验。

在本教程中，你将了解检查数据样本是否偏离正态分布的重要性，以及一套可用于评估你的数据样本的技术。

完成本教程后，您将了解：

样本是否正态决定了可以使用哪些统计方法来处理数据样本。
用于定性评估偏离正态性的图形方法，例如直方图和Q-Q图。
用于定量评估偏离正态性的统计正态性检验。

开始你的项目，阅读我的新书《机器学习统计学》，其中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

2018年5月更新：感谢 Elie，更新了 Anderson-Darling 检验结果的解释。
2018年5月更新：更新了关于“拒绝”与“未能拒绝”H0的语言。

A Gentle Introduction to Normality Tests in Python

Python 正态性检验简明入门
照片由 Ramoun Cabuhay 拍摄，保留部分权利。

教程概述

本教程分为5个部分，它们是：

正态性假设
测试数据集
视觉正态性检查
统计正态性检验
应该使用哪种检验？

需要机器学习统计学方面的帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

正态性假设

统计学领域的很大一部分关注于假定数据是从高斯分布中抽取的数据。

如果使用假设高斯分布的方法，而你的数据是从不同的分布中抽取的，那么结果可能会产生误导，甚至是错误的。

有许多技术可以用来检查你的数据样本是否为高斯分布，或者是否足够接近高斯分布以使用标准技术，或者是否足够非高斯分布以使用非参数统计方法。

这是在为你的数据样本选择统计方法时的一个关键决策点。我们可以将此决策总结如下：

If Data Is Gaussian:
	Use Parametric Statistical Methods
Else:
	Use Nonparametric Statistical Methods

如果数据是高斯分布

使用参数统计方法

否则

使用非参数统计方法

也存在一些折衷方案，我们可以假定数据“足够高斯”以使用参数方法，或者我们可以使用数据准备技术来转换数据，使其足够高斯以使用参数方法。

在机器学习项目中，你可能需要在三个主要领域进行数据样本的这种评估；它们是：

输入模型的数据，用于拟合模型。
模型评估结果，用于模型选择。
模型预测的残差误差，用于回归。

在本教程中，我们将研究两类用于检查数据样本是否为高斯分布的技术：

图形方法。这些方法通过绘制数据来定性评估数据是否看起来像高斯分布。
统计检验。这些方法计算数据的统计量，并量化数据从高斯分布中抽取的可能性。

这些类型的方法通常称为正态性检验。

测试数据集

在开始查看正态性检验之前，让我们先开发一个将在整个教程中使用的测试数据集。

我们将生成一个从高斯分布中提取的小样本随机数。

选择高斯随机数作为测试数据集意味着我们期望每个检验都能正确地识别分布，尽管相对较小的样本量可能会给结果带来一些噪声。

我们将使用 NumPy 的 randn() 函数生成均值为 0，标准差为 1 的随机高斯数，也称为标准正态变量。然后，我们将它们平移，使其均值为 50，标准差为 5。

完整的示例如下所示。

# generate gaussian data
from numpy.random import seed
from numpy.random import randn
from numpy import mean
from numpy import std
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(100) + 50
# summarize
print('mean=%.3f stdv=%.3f' % (mean(data), std(data)))

# 生成高斯数据

from numpy.random import seed

from numpy.random import randn

from numpy import mean

from numpy import std

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

data = 5 * randn(100) + 50

# 总结

print('mean=%.3f stdv=%.3f' % (mean(data), std(data)))

运行示例会生成样本并打印样本的均值和标准差。

我们可以看到，考虑到相对较小的样本量，均值和标准差是真实潜在总体均值和标准差的合理但粗略的估计。

mean=50.303 stdv=4.426

1	mean=50.303 stdv=4.426

视觉正态性检查

我们可以创建数据图来检查它是否是高斯分布。

这些检查是定性的，因此不如我们将在下一节中计算的统计方法准确。尽管如此，它们速度很快，并且像统计检验一样，在可以对数据样本做出判断之前仍需要进行解释。

在本节中，我们将研究两种用于直观检查数据集是否从高斯分布中提取的常用方法。

直方图

检查数据样本分布的简单且常用的图是直方图。

在直方图中，数据被划分为预先指定数量的组，称为箱（bins）。然后将数据排序到每个箱中，并保留每个箱中的观测次数。

该图显示了 x 轴上的箱，保持其顺序关系，y 轴显示每个箱中的计数。

如果数据样本具有高斯分布，则直方图将显示熟悉的钟形曲线。

可以使用 matplotlib 的 hist() 函数创建直方图。默认情况下，箱的数量会根据数据样本自动估算。

下面列出了在测试问题上演示直方图的完整示例。

# histogram plot
from numpy.random import seed
from numpy.random import randn
from matplotlib import pyplot
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(100) + 50
# histogram plot
pyplot.hist(data)
pyplot.show()

# 直方图

from numpy.random import seed

from numpy.random import randn

from matplotlib import pyplot

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

data = 5 * randn(100) + 50

# 直方图

pyplot.hist(数据)

pyplot.show()

运行示例会创建直方图，显示每个箱中的观测数量。

我们可以看到数据呈现出类似高斯分布的形状，虽然不像熟悉的钟形曲线那样明显，但它是一个粗略的近似。

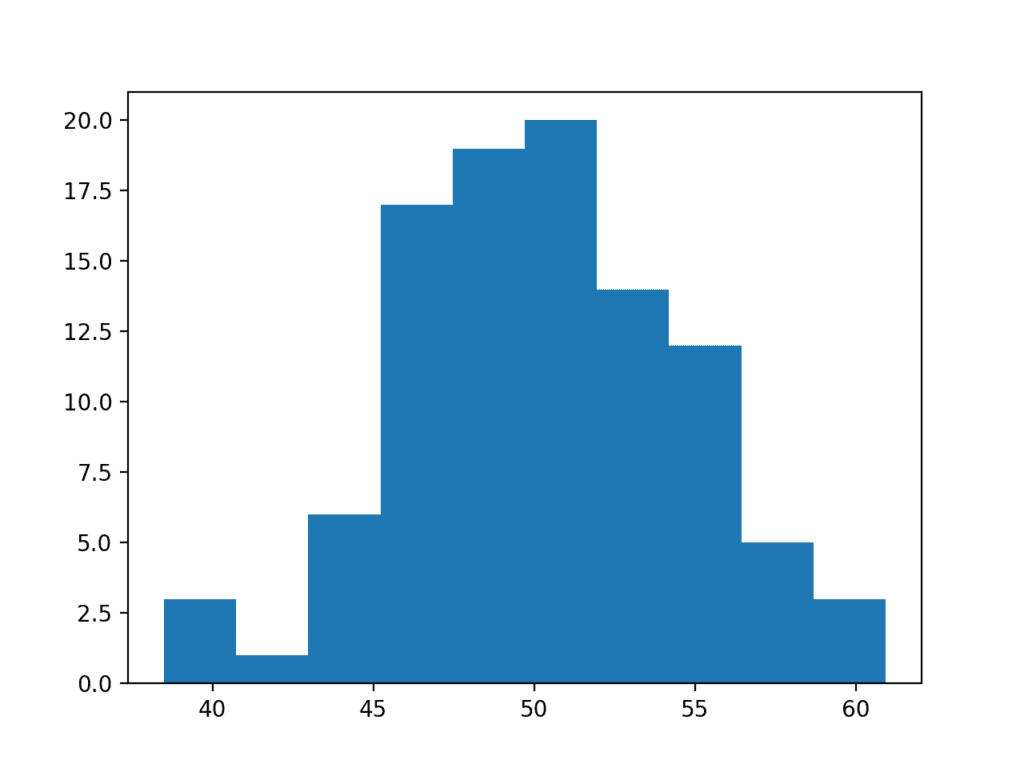
直方图正态性检查

分位数-分位数图

检查数据样本分布的另一个流行图是分位数-分位数图，简称 Q-Q 图或 QQ 图。

此图生成其自身的、与我们正在比较的理想化分布（在此例中为高斯分布）样本。理想化样本被分成组（例如 5 个），称为分位数。样本中的每个数据点都与理想化分布中具有相同累积分布的类似成员配对。

所得点以散点图的形式绘制，理想值在 x 轴上，数据样本在 y 轴上。

如果数据点完美匹配分布，将显示为一条从图的左下角到右上角的 45 度角直线。通常会在图上绘制一条线以帮助明确此预期。点偏离直线表示偏离了预期的分布。

我们可以使用 statsmodels 的 qqplot() 函数在 Python 中开发 QQ 图。该函数接受数据样本，并默认假定我们将其与高斯分布进行比较。我们可以通过将“line”参数设置为“s”来绘制标准化线。

下面提供了将测试数据集绘制为 QQ 图的完整示例。

# QQ Plot
from numpy.random import seed
from numpy.random import randn
from statsmodels.graphics.gofplots import qqplot
from matplotlib import pyplot
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(100) + 50
# q-q plot
qqplot(data, line='s')
pyplot.show()

# QQ 图

from numpy.random import seed

from numpy.random import randn

from statsmodels.graphics.gofplots import qqplot

from matplotlib import pyplot

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

data = 5 * randn(100) + 50

# q-q 图

qqplot(data, line='s')

pyplot.show()

运行示例会创建 QQ 图，显示散点图的点呈对角线排列，与来自高斯分布的样本的预期对角线模式非常吻合。

存在一些小的偏差，尤其是在图的底部，考虑到小样本量，这是可以预期的。

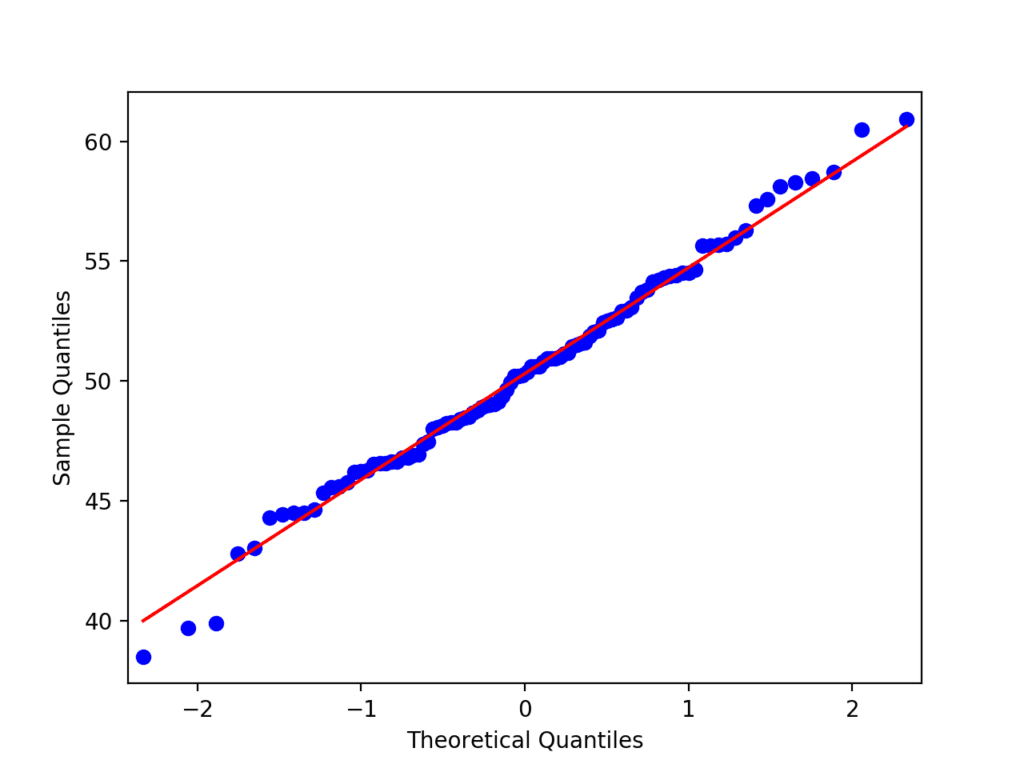
QQ 图正态性检查

统计正态性检验

我们可以使用许多统计检验来量化数据样本是否看起来像是从高斯分布中抽取的。

每种检验都有不同的假设，并考虑数据的不同方面。

在本节中，我们将介绍三种常用的检验，你可以将它们应用于自己的数据样本。

检验的解释

在应用统计检验之前，你必须知道如何解释结果。

每种检验至少会返回两项内容：

统计量：由检验计算出的一个量，可以通过将其与假设检验的临界值进行比较，在检验的上下文中进行解释。
p 值：用于解释检验，在此例中用于确定样本是否从高斯分布中抽取。

每种检验都会计算一个特定于检验的统计量。这个统计量可以帮助解释结果，尽管它可能需要更深的统计学知识和对特定统计检验更深的了解。相反，p 值可以用于在实际应用中快速准确地解释统计量。

这些检验假定样本是从高斯分布中抽取的。技术上这被称为零假设，或 H0。选择一个称为 alpha 的阈值水平，通常是 5%（或 0.05），用于解释 p 值。

在这些检验的 SciPy 实现中，你可以按如下方式解释 p 值：

p <= alpha：拒绝 H0，非正态。
p > alpha：未能拒绝 H0，正态。

这意味着，总的来说，我们正在寻找 p 值较大的结果来确认我们的样本很可能来自高斯分布。

大于 5% 的结果并不意味着零假设为真。它意味着考虑到现有证据，它很可能是真的。p 值不是数据符合高斯分布的概率；它可以被认为是帮助我们解释统计检验的一个值。

夏皮罗-威尔克检验 (Shapiro-Wilk Test)

Shapiro-Wilk 检验评估数据样本，并量化数据是从高斯分布中抽取的可能性，以 Samuel Shapiro 和 Martin Wilk 的名字命名。

在实践中，Shapiro-Wilk 检验被认为是一个可靠的正态性检验，尽管有建议认为该检验可能适用于较小样本的数据，例如数千个观测或更少。

SciPy 的 shapiro() 函数可以计算给定数据集的 Shapiro-Wilk 检验。该函数同时返回检验计算的 W 统计量和 p 值。

下面列出了对数据集执行 Shapiro-Wilk 检验的完整示例。

# Shapiro-Wilk Test
from numpy.random import seed
from numpy.random import randn
from scipy.stats import shapiro
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(100) + 50
# normality test
stat, p = shapiro(data)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
	print('Sample looks Gaussian (fail to reject H0)')
else:
	print('Sample does not look Gaussian (reject H0)')

# Shapiro-Wilk 检验

from numpy.random import seed

from numpy.random import randn

from scipy.stats import shapiro

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

data = 5 * randn(100) + 50

# 正态性检验

stat, p = shapiro(data)

print('Statistics=%.3f, p=%.3f' % (stat, p))

# 解释

alpha = 0.05

if p > alpha:

print('样本看起来是高斯分布 (未能拒绝 H0)')

else:

print('样本看起来不像高斯分布 (拒绝 H0)')

运行示例会首先计算数据样本上的检验，然后打印统计量和计算出的 p 值。

p 值很有趣，并且发现数据很可能来自高斯分布。

Statistics=0.992, p=0.822
Sample looks Gaussian (fail to reject H0)

1 2	Statistics=0.992, p=0.822 样本看起来是高斯分布 (未能拒绝 H0)

D’Agostino’s K^2 检验

D’Agostino’s K^2 检验通过计算数据的汇总统计量，即峰度和偏度，来确定数据分布是否偏离正态分布，以 Ralph D’Agostino 的名字命名。

偏度是量化分布向左或向右倾斜的程度，是分布不对称性的度量。
峰度量化了分布在尾部的程度。这是一个简单且常用的正态性统计检验。

D’Agostino’s K^2 检验可通过 SciPy 的 normaltest() 函数获得，并返回检验统计量和 p 值。

下面列出了对数据集执行 D’Agostino’s K^2 检验的完整示例。

# D'Agostino and Pearson's Test
from numpy.random import seed
from numpy.random import randn
from scipy.stats import normaltest
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(100) + 50
# normality test
stat, p = normaltest(data)
print('Statistics=%.3f, p=%.3f' % (stat, p))
# interpret
alpha = 0.05
if p > alpha:
	print('Sample looks Gaussian (fail to reject H0)')
else:
	print('Sample does not look Gaussian (reject H0)')

# D'Agostino 和 Pearson 检验

from numpy.random import seed

from numpy.random import randn

from scipy.stats import normaltest

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

data = 5 * randn(100) + 50

# 正态性检验

stat, p = normaltest(data)

print('Statistics=%.3f, p=%.3f' % (stat, p))

# 解释

alpha = 0.05

if p > alpha:

print('样本看起来是高斯分布 (未能拒绝 H0)')

else:

print('样本看起来不像高斯分布 (拒绝 H0)')

运行示例会计算统计量并打印统计量和 p 值。

p 值与 5% 的 alpha 值进行比较，发现测试数据集与正态分布没有显著偏离。

Statistics=0.102, p=0.950
Sample looks Gaussian (fail to reject H0)

1 2	Statistics=0.102, p=0.950 样本看起来是高斯分布 (未能拒绝 H0)

安德森-达令检验 (Anderson-Darling Test)

Anderson-Darling 检验是一种统计检验，可用于评估数据样本是否来自众多已知数据样本之一，以 Theodore Anderson 和 Donald Darling 的名字命名。

它可用于检查数据样本是否为正态。该检验是更复杂的非参数拟合优度统计检验 Kolmogorov-Smirnov 检验的修改版本。

Anderson-Darling 检验的一个特点是它返回一个临界值列表，而不是一个单一的 p 值。这可以为更彻底地解释结果提供基础。

SciPy 的 anderson() 函数实现了 Anderson-Darling 检验。它接受数据样本和要检验的分布名称作为参数。默认情况下，该检验将与高斯分布进行比较（dist=’norm’）。

下面列出了在样本问题上计算 Anderson-Darling 检验的完整示例。

# Anderson-Darling Test
from numpy.random import seed
from numpy.random import randn
from scipy.stats import anderson
# seed the random number generator
seed(1)
# generate univariate observations
data = 5 * randn(100) + 50
# normality test
result = anderson(data)
print('Statistic: %.3f' % result.statistic)
p = 0
for i in range(len(result.critical_values)):
	sl, cv = result.significance_level[i], result.critical_values[i]
	if result.statistic < result.critical_values[i]:
		print('%.3f: %.3f, data looks normal (fail to reject H0)' % (sl, cv))
	else:
		print('%.3f: %.3f, data does not look normal (reject H0)' % (sl, cv))

# Anderson-Darling 检验

from numpy.random import seed

from numpy.random import randn

from scipy.stats import anderson

# 为随机数生成器设置种子

seed(1)

# 生成单变量观测值

data = 5 * randn(100) + 50

# 正态性检验

result = anderson(data)

print('Statistic: %.3f' % result.statistic)

p = 0

for i in range(len(result.critical_values)):

sl, cv = result.significance_level[i], result.critical_values[i]

if result.statistic < result.critical_values[i]:

print('%.3f: %.3f, 数据看起来是正态的 (未能拒绝 H0)' % (sl, cv))

else:

print('%.3f: %.3f, 数据看起来不是正态的 (拒绝 H0)' % (sl, cv))

运行示例会计算测试数据集上的统计量并打印临界值。

统计检验中的临界值是一系列预定义的显著性边界，如果计算出的统计量小于临界值，则可以在这些边界处未能拒绝 H0。该检验返回一系列常用的显著性水平的临界值，而不是单个 p 值。

我们可以通过在选定的显著性水平下，如果计算出的检验统计量小于临界值，则未能拒绝数据为正态的零假设来解释结果。

我们可以看到，在每个显著性水平上，检验都发现数据遵循正态分布

Statistic: 0.220
15.000: 0.555, data looks normal (fail to reject H0)
10.000: 0.632, data looks normal (fail to reject H0)
5.000: 0.759, data looks normal (fail to reject H0)
2.500: 0.885, data looks normal (fail to reject H0)
1.000: 1.053, data looks normal (fail to reject H0)

Statistic: 0.220

15.000: 0.555, 数据看起来是正态的 (未能拒绝 H0)

10.000: 0.632, 数据看起来是正态的 (未能拒绝 H0)

5.000: 0.759, 数据看起来是正态的 (未能拒绝 H0)

2.500: 0.885, 数据看起来是正态的 (未能拒绝 H0)

1.000: 1.053, 数据看起来是正态的 (未能拒绝 H0)

应该使用哪种检验？

我们已经介绍了一些正态性检验，但这并不是存在的全部检验。

那么，你应该使用哪种检验？

我建议在适当的情况下，将它们全部用于你的数据。

问题就变成，你如何解释结果？如果检验结果不一致怎么办，它们经常会这样做？

我为你提供了两个建议来帮助你思考这个问题。

硬性失败

你的数据可能出于多种原因而非正态。每种检验都从略微不同的角度审视样本是否来自高斯分布的问题。

一种正态性检验的失败意味着你的数据不是正态的。就是这么简单。

你可以调查你的数据为什么不是正态的，并可能使用数据准备技术使数据更正态。

或者你可以开始考虑使用非参数统计方法，而不是参数方法。

软性失败

如果一些方法表明样本是高斯分布而另一些则不是，那么也许可以将其视为数据近似高斯分布的指示。

在许多情况下，你可以将你的数据视为高斯分布，并继续使用你选择的参数统计方法。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

列出另外两个在机器学习项目中可能使用正态性检验的示例。
开发你自己的人为数据集，并应用每种正态性检验。
加载一个标准机器学习数据集，并对每个实值变量应用正态性检验。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

API

文章

总结

在本教程中，你了解了检查数据样本是否偏离正态分布的重要性，以及一套可用于评估数据样本的技术。

具体来说，你学到了：

样本是否正态决定了可以使用哪些统计方法来处理数据样本。
用于定性评估偏离正态性的图形方法，例如直方图和 Q-Q 图。
用于定量评估偏离正态性的统计正态性检验。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

非参数统计入门指南

统计假设检验入门指南

128 条对《Python 正态性检验入门指南》的回复

Elie Kawerk 2018年5月11日上午5:43 #

嗨，Jason，

感谢这篇精彩的文章。在 Anderson-Darling 检验段落中，最后一句话是否应该是

“我们可以看到，在每个显著性水平上，检验都发现了数据遵循正态分布”

而不是

“我们可以看到，在每个显著性水平上，检验都发现了与正态分布的显著偏离。”

祝好，
Elie

回复
- Jason Brownlee 2018年5月11日上午6:43 #
  
  抓得好，谢谢！已修复。
  
  回复
Nouroz 2018年5月11日上午7:40 #

未能拒绝一个假设并不意味着你接受它。😀

回复
- Jason Brownlee 2018年5月11日上午7:54 #
  
  这意味着什么？
  
  回复
  - Bhaskar 2018年5月24日下午3:51 #
    
    你不能对那个假设说什么。
    
    回复
    - Ravinder 2018年9月4日上午2:10 #
      
      H0：数据是正态的
      H1：数据不是正态的
      p > alpha：未能拒绝 H0 (没有足够的证据证明数据是正态的)
      阅读此文
      https://stackoverflow.com/questions/7781798/seeing-if-data-is-normally-distributed-in-r/7788452#7788452
      
      回复
Vinay 2018年5月11日上午11:52 #

你好，

写得真好。谢谢你的文章。既然我们知道了数据是否正态分布，如何将非正态分布的数据转换为正态分布？Boxcox 是唯一的方法，还是你更倾向于其他方法？

回复
- Jason Brownlee 2018年5月11日下午2:31 #
  
  谢谢。
  
  很棒的问题！我有一篇关于这个确切问题的帖子已经安排好了。请稍候几天。
  
  回复
  - Vinay 2018年5月15日晚上9:42 #
    
    太棒了！谢谢。
    
    回复
- Sumithra 2021年7月29日上午3:13 #
  
  你也可以进行对数转换和其他一些技术
  
  回复
Raj 2018年5月11日下午2:47 #

再次感谢这篇好文章。

回复
- Jason Brownlee 2018年5月12日上午6:25 #
  
  很高兴它有帮助。
  
  回复
Akhilesh 2018年5月13日下午6:08 #

极好的文章。我喜欢你强调根据手头数据接近正态与否来使用参数或非参数模型来拟合 ML 模型的部分。我认为大多数书籍并没有明确说明这一点。

回复
- Jason Brownlee 2018年5月14日上午6:33 #
  
  谢谢，很高兴对您有帮助。
  
  回复
Tarlan Mammadov 2018年5月20日上午6:59 #

Jason，这是一篇很棒的文章，谢谢！那么，在数据集有多个实值特征的情况下，我们是否应该对每个特征进行此检验，然后如果其中一个或多个特征被证明是非高斯分布，是否意味着整个数据集是非高斯分布？或者我们应该通过数据准备步骤来处理非高斯特征？

此外，您是否有关于各种机器学习算法的归纳偏置的类似帖子？

回复
- Jason Brownlee 2018年5月21日上午6:20 #
  
  我们会一次处理一个变量。
  
  归纳偏置是一种抽象，用于理解算法设计决策如何影响假设映射的搜索/选择，它并不是一个真正可衡量的量。
  
  回复
Bhaskar 2018年5月24日下午4:45 #

零假设 (H0) 不应该是假设我们的数据是正态的吗？

回复
- Jason Brownlee 2018年5月25日上午9:19 #
  
  正确，H0 是数据是正态的。
  
  回复
Mamta 2018年5月25日下午7:08 #

很棒的文章..
我尝试了进一步的扩展：“加载一个标准机器学习数据集，并对实值变量应用正态性检验。”

链接： https://github.com/Mamtasadani/Normality-Test-v

请给我您的宝贵建议..

回复
- Jason Brownlee 2018年5月26日上午5:52 #
  
  做得好，但你的链接坏了。
  
  回复
  - Mamta 2018年5月26日上午10:06 #
    
    抱歉上面的链接
    
    请检查此链接
    
    https://github.com/Mamtasadani/Normality-Test-
    
    谢谢
    
    回复
    - Jason Brownlee 2018年5月27日上午6:43 #
      
      干得好！
      
      回复
Krzysztof 2018年6月22日下午3:30 #

嗨，Jason，

我目前正在从事一个时间序列预测项目。我主要使用 RNN（LSTM）机器学习模型进行预测。我所处理的时间序列的常态性（或非常态性）会影响我构建模型的方式吗？还是说 LSTM 即使在处理非正态数据时也能表现良好？简单来说，我在使用 LSTM 时是否应该始终将我的时间序列正态化？

Krzysztof

回复
- Jason Brownlee 2018年6月23日上午6:12 #
  
  这可能会有影响，这 realmente取决于具体问题。我建议评估多种不同的输入数据准备方式。
  
  回复
Dom 2018年7月10日下午3:09 #

嗨
您会如何分析像薪资数据那样高度右偏的数据，即少数人赚很多钱，而其余大部分人收入在中等/较低范围？
谢谢

回复
- Jason Brownlee 2018年7月11日上午5:51 #
  
  听起来像是幂律分布或指数分布，而不是高斯分布。
  
  回复
Vips 2018年8月4日下午12:22 #

这可能是我在搜索数小时后找到的唯一合乎逻辑且解释得最好的教程。我已将此添加到书签，并将一遍又一遍地参考它。非常感谢您的努力，Brownlee 博士！

回复
- Jason Brownlee 2018年8月5日上午5:22 #
  
  谢谢，很高兴听到这个。
  
  回复
Jorge 2018年8月15日下午7:23 #

我进行了 alpha = 0.05 的 Shapiro-Wilk 检验，得到了 p 值 = 0.04，拒绝了原假设。D’Agostino K-square 检验的 p 值为 0.191，未拒绝原假设；Anderson-Darling 检验对于四个临界值拒绝了原假设，而对于一个临界值未拒绝原假设。您建议我接下来怎么做？

和

只是确认一下，如果我的数据拒绝了原假设（非正态），我是否不应该使用任何基于高斯分布的模型（机器学习模型），例如高斯过程或指数平滑？

如果我想使用它们，我是否应该对数据进行处理？？

谢谢你

回复
- Jason Brownlee 2018年8月16日上午6:02 #
  
  每个检验都提供了对数据正态性的不同视角，您必须结合您的项目/目标来解释结果。
  
  请参阅：“您应该使用哪种检验？” 部分
  
  回复
  - Marcos 2020年2月4日下午1:21 #
    
    非常感谢这个介绍，我已经全部实现来测试我的数据。我对 Anderson-Darling 检验中显著性水平的解释有些疑问。通俗地说：H0 被 2.5% 的水平拒绝但未被 5% 的水平拒绝是什么意思？百分比是多少？也就是说，在哪个水平您会相信输入数据是高斯的？5%？10%？
    
    也许有一个“不太高斯”的例子会很有用，这样它就能通过 5 个显著性水平中的 2 个
    
    回复
    - Jason Brownlee 2020年2月4日下午2:17 #
      
      谢谢，很高兴它有帮助！
      
      这些概率代表事件是真实的还是数据中的统计异常的可能性。我们永远无法确定，但我们可以使用统计检验来谈论可能性。
      
      通常，您会选择可用的最强的水平，例如 5%。超过 5%（20分之一）时，我们通常会放弃并说它可能不是真的。
      
      回复
      - Marcos 2020年2月4日晚上11:48 #
        
        好的！
        
        那么，为了澄清，如果统计值小于 15% 的临界值（不拒绝 H0），我就可以确信该分布是高斯的。如果不是（统计值大于临界值），则检查 10%。如果不是，则检查 5%。如果我无法通过 5% 的检验，就不必考虑 2.5% 或 1% 了，对吗？
        
        这是我结合视觉和统计检验的方法，非常希望能得到您的意见。
        
        https://gist.github.com/marnunez/6c68248fee14236dab42ef3e46b94116
        
        再次感谢您的一切！
      - Jason Brownlee 2020年2月5日上午8:15 #
        
        通常只使用 0.05，例如 5% 的水平。
        
        更多信息在这里
        https://machinelearning.org.cn/faq/single-faq/how-do-i-interpret-a-p-value
xkcd 2018年8月19日凌晨12:18 #

极好的文章！

您是否有一些关于如何检验多峰分布数据的组成部分是否服从正态分布的建议？

回复
- Jason Brownlee 2018年8月19日上午6:25 #
  
  哎呀，为什么？
  
  嗯，如果非要这么做，您可以重新定义分布，然后剔除一个您认为呈钟形的元素并对其进行检验。在我看来，这听起来很危险且无效。
  
  我预计如果您与真正的统计学家交流，会有更好的方法！也许可以去 math stackoverflow 上发帖询问在此情况下最佳实践。
  
  回复
Makis 2018年9月14日下午7:16 #

你好 Jason，

惊人的教程。

我想知道 Python 中是否有任何函数可以评估多元正态性？

在 R 中，有 MVN 包可以做到这一点（https://cran.r-project.cn/web/packages/MVN/vignettes/MVN.pdf）。

祝好，
Makis

回复
- Jason Brownlee 2018年9月15日上午6:04 #
  
  谢谢。
  
  好问题，可能确实有。我一时说不准。
  
  如果您找到了什么，请告诉我。
  
  回复
Jk 2018年11月11日下午8:17 #

我理解在回归模型中检验残差的重要性。但我对您提到的其他两个用途不清楚（在拟合模型的情况下输入模型数据。
模型评估中的模型选择结果）。您能指出一个资源来进一步解释吗？

回复
- Jason Brownlee 2018年11月12日上午5:38 #
  
  嗯，关于比较算法，您可以从这里开始
  https://machinelearning.org.cn/statistical-significance-tests-for-comparing-machine-learning-algorithms/
  
  回复
Emily Stander 2018年12月19日晚上11:59 #

嗨，Jason，

这篇帖子是否已发布？您能链接一下吗？

谢谢！

回复
- Jason Brownlee 2018年12月20日上午6:26 #
  
  Emily，您具体指的是哪篇帖子？
  
  回复
Anirban 2019年1月4日凌晨2:24 #

在什么情况下了解我们数据的分布会有帮助？请分享一些例子！

回复
- Jason Brownlee 2019年1月4日上午6:32 #
  
  几乎总是如此——有助于数据准备和模型选择。
  
  回复
- RAJESH 2020年11月24日下午3:37 #
  
  嗨，Jason，
  
  您的所有文章都非常有信息量且有帮助。
  
  我只是想知道 KS 检验是否对数据正态化敏感？因为我在数据正态化和非正态化时得到了完全不同的结果。
  
  它是否期望我的数据集的均值和标准差为 0、1。
  
  但是，其他测试，如 AD 和 D’agastino，不受影响。
  
  回复
  - Jason Brownlee 2020年11月25日上午6:39 #
    
    谢谢。
    
    从您的结果来看，我猜是的。我建议您查阅文档。
    
    回复
Antonio 2019年2月7日凌晨2:59 #

你好，

感谢您对如何对自己的数据执行正态性检验的良好解释。

如何将非正态数据转换为正态数据？

再次感谢！

回复
- Jason Brownlee 2019年2月7日上午6:44 #
  
  这取决于它有多么不服从正态分布。
  
  例如，可能需要删除异常值，或者使用 Box-Cox 变换等幂变换来修复简单问题。
  
  回复
Nasim 2019年2月8日上午6:36 #

嗨，Jason，
感谢这篇文章。我想知道，如果我想将这些检验应用于流数据，那么合适的时间窗口大小（窗口大小 = 样本数量）是多少？我可以在流数据上使用滑动窗口应用这些检验吗？

回复
- Jason Brownlee 2019年2月8日上午8:07 #
  
  好问题，我一时说不准。我预计可能存在处理流数据的特定方法。
  
  如果没有，那么收集一段时间的代表性样本可能是一个好的开始。
  
  回复
dongliang 2019年2月16日晚上11:37 #

有帮助，谢谢！

回复
- Jason Brownlee 2019年2月17日上午6:29 #
  
  谢谢。
  
  回复
Raz 2019年3月8日凌晨2:09 #

嗨，Jason，

很棒的教程。我正在使用 Shapiro-Wilk 检验来检查我的数据是否服从正态分布。我有两个样本分布，当它们单独测试时，检验结果表明它们服从高斯分布。但将两者合并成一个更大的样本后，检验结果则显示相反。

我应该关注合并后数据的正态性吗？
我正试图比较这两个样本分布，以检查它们是否存在显著差异。

回复
- Jason Brownlee 2019年3月8日上午7:54 #
  
  如果它们是独立的样本，那么将它们合并可能没有意义。
  
  回复
Samik 2019年3月11日晚上8:41 #

嗨，Jason，

关于如果数据不服从正态分布的纠正措施，您有什么建议吗？特别是指残差图。

回复
- Jason Brownlee 2019年3月12日上午6:49 #
  
  是的，请看这篇文章
  https://machinelearning.org.cn/how-to-transform-data-to-fit-the-normal-distribution/
  
  回复
AK 2019年3月14日凌晨1:00 #

你好 jason,

我们如何检验多维特征数据的正态性？假设我有 20 个特征，我应该如何知道是运行（普通）线性回归，还是应该考虑交互项或将某些特征转换为平方项等等？我们如何才能知道这一点。

回复
- Jason Brownlee 2019年3月14日上午9:25 #
  
  作为开始，也许可以逐个特征进行？
  
  回复
Mattia Ducci 2019年5月11日晚上10:19 #

感谢您提供像这样的教程！一如既往的清晰。

回复
- Jason Brownlee 2019年5月12日上午6:43 #
  
  很高兴它有帮助。
  
  回复
B Chandrashekar 2019年5月30日晚上9:37 #

这是一篇很棒的文章。非常有帮助地理解了这些概念。
希望您能提供更多好文章。
谢谢你

回复
- Jason Brownlee 2019年5月31日上午7:49 #
  
  谢谢，很高兴对您有帮助。
  
  回复
AR 2019年5月31日凌晨4:17 #

感谢这篇精彩的教程。我有一个后续问题，希望您能帮助我。

我有几个数据集需要计算样本统计量，如均值、方差等。在应用了您建议的检验后，我发现许多数据集并非服从正态分布，我想知道您是否对应该遵循的步骤有任何建议。其余大部分数据集似乎服从指数分布。谢谢。

回复
- Jason Brownlee 2019年5月31日上午7:55 #
  
  这取决于您想用这些数据做什么，以及您可能想采取什么行动。
  
  例如，使用线性算法进行建模需要输入服从高斯分布。使用其他模型则没有这个要求。
  
  回复
Sahil 2019年6月7日凌晨1:11 #

你好，

感谢您分享如此有信息量的帖子。有没有办法检查整个数据集的正态性？假设我的数据集中有 50 列，我想检查我的数据是否偏离高斯分布，我能做到吗？
提前感谢

回复
- Jason Brownlee 2019年6月7日上午8:05 #
  
  逐列进行。
  
  尽可能避免多元高斯分布，因为它会变得非常复杂（对我来说）。
  
  回复
Alok 2019年6月18日晚上10:23 #

如果观测数量非常大，接近 40,000 次观测，该怎么办？
正态性检验是否仍然有效？

回复
- Jason Brownlee 2019年6月19日上午7:56 #
  
  很棒的问题。
  
  很可能，但几乎所有的统计检验都是为小数据设计的。我认为在处理大数据时其有效性是一个重大的开放性问题——例如，罕见事件/异常值出现的可能性增加。
  
  回复
  - Tushar 2019年7月20日晚上10:38 #
    
    那么在这种情况下，我们是否应该将数据分成小块并检验这些小块的“高斯性”，而那些不符合检验的小块，是否应该进行审查，并在需要时从我们正在处理的数据集中删除？
    
    回复
    - Jason Brownlee 2019年7月21日上午6:30 #
      
      我不赞成这种方法，结果的方差会太大。
      
      回复
Tushar 2019年7月20日晚上10:35 #

你好Jason
感谢您的这篇帖子。它非常有信息量。您能否告诉我为什么没有包含 Dickey Fuller 检验？我的意思是，根据我读过的其他帖子，Dickey Fuller 检验是谈论最多的。所以，您选择这三个检验而不是 Dickey Fuller 检验，是否有特定的原因？

回复
- Tushar 2019年7月20日晚上10:40 #
  
  抱歉，名字拼写错了。Jason，希望您不介意，我想我把它拼错了，因为在当今世界，JSON 是我们遇到的最常见的东西了 :)
  
  回复
  - Jason Brownlee 2019年7月21日上午6:30 #
    
    不客气。
    
    回复
- Jason Brownlee 2019年7月21日上午6:29 #
  
  它在这里被涵盖为平稳性检验。
  https://machinelearning.org.cn/time-series-data-stationary-python/
  
  回复
Masfiq 2019年7月23日下午4:16 #

这非常有帮助。现在我有一个数据集。它不是正态的。我的数据集的直方图看起来是这样的。

.
....
……..
…………
…………………..
……………………….

现在我该如何设计一个模型（用于重新生成这些数据）？

回复
- Jason Brownlee 2019年7月24日上午7:48 #
  
  也许选择一个适合数据的概率分布，或者使用密度估计进行建模，然后使用模型通过概率生成新实例。
  
  回复
William G. 2019年8月26日凌晨2:49 #

谢谢，好文章。如何将这些工具与 Pandas DataFrame 的输入一起使用？

回复
- Jason Brownlee 2019年8月26日上午6:22 #
  
  从 DataFrame 中提取 NumPy 数组（.values）即可！
  
  回复
  - William G. 2019年8月26日晚上6:02 #
    
    谢谢您的回答 Jason，我尝试过，例如用这个
    
    results = pd.DataFrame.from_records(all_stats, columns=[‘Sales’,
    ‘Commission_Amount’,
    ‘Sales_Target’])
    stat, p = shapiro(results.values)
    print(‘Statistics=%.3f, p=%.3f’ % (stat, p))
    # 解释
    alpha = 0.05
    if p > alpha
    print(‘Sample looks Gaussian (fail to reject H0)’)
    else
    print(‘Sample does not look Gaussian (reject H0)’)
    
    但是 p 值总是 0.000。希望您能帮我，非常感谢。谢谢！
    
    回复
    - Jason Brownlee 2019年8月27日凌晨6:36 #
      
      也许可以仔细检查一下您是否正确加载了数据？
      
      回复
      - William G. 2019年8月27日晚上7:41 #
        
        非常感谢您的帮助，谢谢。我的数据输出看起来是正确的
        
        [[82024750. 2809815. 82350000.]
        [86901250. 2970088. 87000000.]
        [81341500. 2776092. 81375000.]
        …
        [85586000. 2933965. 85875000.]
        [82237250. 2742930. 83025000.]
        [82130000. 2748805. 82875000.]]
        
        我总是得到这样的结果
        “Statistics=0.642, p=0.000”
        
        我应该改变什么吗？
        谢谢！
      - Jason Brownlee 2019年8月28日凌晨6:32 #
        
        结果表明数据不是高斯分布。
Yoon 2019年10月3日上午7:29 #

关于使用 QQ 图来检查正态分布，我们可以简单地绘制数据点，还是应该抽取随机样本的均值来与理论值绘制？根据中心极限定理，它是否说明样本均值最终会呈现高斯分布？对于 shapiro 检验，当样本超过 5000 时，我会收到警告。是否有更适合大样本的检验？

回复
- Jason Brownlee 2019年10月3日下午1:25 #
  
  直接绘制数据点即可。
  
  回复
Daniel W. 2019年10月9日晚上9:43 #

不错的文章！我正在学习 shapiro-wilk 检验，但我不明白。
statistics、p 和 alpha 分别代表什么？

谢谢你的回答，伙计！

回复
- Jason Brownlee 2019年10月10日上午6:58 #
  
  也许这会有帮助。
  https://machinelearning.org.cn/faq/single-faq/how-do-i-interpret-a-p-value
  
  回复
Ravi Kumar 2019年10月24日凌晨3:44 #

你好，

我正在检验我的两个样本是否有不同的均值。为此，我首先检验这两个样本的正态性。假设它们不是正态的，并且在转换后它们变成了正态。现在，如果我对转换后的数据执行双样本 t 检验，关于相同/不同均值的结论是否适用于原始数据？

回复
- Ravi Kumar 2019年10月24日凌晨4:07 #
  
  另外，如果数据不是正态的，双样本 t 检验的替代方法是什么？
  
  回复
  - Jason Brownlee 2019年10月24日上午5:46 #
    
    您可以使用 Mann-Whitney U 检验。
    https://machinelearning.org.cn/nonparametric-statistical-significance-tests-in-python/
    
    回复
- Jason Brownlee 2019年10月24日上午5:45 #
  
  很好的问题！
  
  不，它适用于转换后的数据。
  
  您可能想使用秩检验
  https://machinelearning.org.cn/nonparametric-statistical-significance-tests-in-python/
  
  回复
  - Ravi Kumar 2019年10月25日凌晨8:02 #
    
    谢谢您的回答。
    我进行了 Mann-Whitney U 检验，看到 p 值为 0.289，因此得出结论均值在统计上没有显著差异（因为我的 alpha 不能大于 0.15）。
    
    对于第二个评论——
    我只是想得到您的确认。
    您是否说——“不，它仅适用于转换后的数据，而不适用于原始数据（以得出结论）”
    
    感谢您的回复。
    
    回复
    - Jason Brownlee 2019年10月25日下午1:46 #
      
      干得好！
      
      是的，没错。
      
      回复
AJILISA O A 2019年11月22日下午4:59 #

极好的教程，先生……当我处理不平衡分类问题时，大多数实例属于一个类别，使用随机欠采样方法和其他技术形成多个平衡数据集。我们能否使用任何方法来评估每个方法生成的样本的显著性？我们是否需要检查样本是否服从高斯分布？

回复
- Jason Brownlee 2019年11月23日上午6:44 #
  
  谢谢！
  
  不，我认为这种分析不是必需的，也没有意义。
  
  回复
  - AJILISA O A 2019年11月25日下午4:04 #
    
    我们是否需要检查我们提出的方法生成的新样本是否服从原始数据集的分布？
    
    回复
    - Jason Brownlee 2019年11月26日上午5:58 #
      
      我假设它们是多元示例。也许可以研究基于密度的方法，例如单类分类，以查看新示例是否适合或不适合。
      
      回复
Venkatesh Gandi 2019年11月25日凌晨12:52 #

嗨 Jason，好文章。感谢分享知识。所有上述检验的 alpha 值都是 0.05 吗？我们如何将 alpha 值更改为期望值？我看过文档，但找不到答案。您能帮我解决这个问题吗？

回复
- Jason Brownlee 2019年11月25日上午6:30 #
  
  您可以直接指定 alpha 值，使用您想要的任何值，例如 0.01、0.05 甚至 0.1。
  
  回复
Venkatesh Gandi 2019年11月27日晚上9:09 #

嗨 Jason，您能告诉我们如何在 Python 中执行 Cramér–von Mises 正态性检验吗？

回复
- Jason Brownlee 2019年11月28日上午6:35 #
  
  抱歉，我对那个测试不熟悉。它主要是关于什么的？
  
  我在谷歌上找到了这个
  https://pypi.ac.cn/project/scikit-gof/
  
  回复
  - Venkatesh Gandi 2019年11月29日上午7:22 #
    
    谢谢提供的信息。
    
    回复
    - Jason Brownlee 2019年11月29日下午1:39 #
      
      不客气。
      
      回复
Goodman 2020年2月12日上午9:07 #

这太棒了，非常容易理解和系统化！这一个帖子教会了我比三年大学学习更多的关于正态性检验的知识！非常出色，谢谢！

回复
- Jason Brownlee 2020年2月12日下午1:35 #
  
  谢谢，很高兴它有帮助！
  
  回复
San 2020年3月16日下午6:03 #

对于分类变量，使用的图形和统计正态性检验有哪些？

我有一个只有分类变量的数据集。有一个年龄列，代表 3 个类别。其他属性只有 true、false 值。目标属性有 22 个类别。

谢谢
San

回复
- Jason Brownlee 2020年3月17日上午8:11 #
  
  卡方检验是一个不错的起点
  https://machinelearning.org.cn/chi-squared-test-for-machine-learning/
  
  另请参阅此
  https://machinelearning.org.cn/feature-selection-with-categorical-data/
  
  回复
Ahmet 2020年3月23日下午9:36 #

嗨 Jason，你太棒了。我有一个问题。Shapiro-Wilk检验中的W统计量是什么意思？我们如何解释它？

回复
- Jason Brownlee 2020年3月24日上午6:01 #
  
  好问题，这会有帮助
  https://en.wikipedia.org/wiki/Shapiro%E2%80%93Wilk_test
  
  回复
Rishi 2020年5月12日下午5:08 #

嗨 Jason，很棒的文章。关于 Anderson-Darling 检验中的临界值，有一个快速的问题。临界值是否等同于置信水平，例如 15 = 85% 置信度，5 = 95% 置信度，等等？

回复
- Jason Brownlee 2020年5月13日上午6:28 #
  
  关于临界值是什么，这里有更多信息
  https://machinelearning.org.cn/critical-values-for-statistical-hypothesis-testing/
  
  回复
Borja 2020年6月27日下午9:32 #

非常感谢这篇文章。我本来要花十倍于现在的时间来研究正态性检验。我仍然需要自己看更多东西才能更好地理解，但这非常有帮助。
真是一个伟大的时代，我们可以通过谷歌找到许多问题的答案。

回复
- Jason Brownlee 2020年6月28日上午5:48 #
  
  谢谢，很高兴听到这个。
  
  回复
Levani 2020年10月16日上午6:29 #

一个小评论。Q-Q 图不是对角线的，而是线性的。即使这里作为示例显示的 QQ 图也不是对角线的。

回复
- Jason Brownlee 2020年10月16日上午8:08 #
  
  谢谢。
  
  回复
Ankush Jamthikar 2020年10月28日下午4:08 #

我是一名统计学和机器学习的初学者。你对正态性检验的解释非常好！我只有一个问题。在机器学习算法中，我们使用特征来执行分类任务，这些正态性检验有什么影响？我的意思是，即使特征不是正态分布的，它们仍然可以为分类过程做出贡献，而且可能也很重要？

回复
- Jason Brownlee 2020年10月29日上午7:55 #
  
  谢谢！
  
  它们可能只在您使用假定或要求输入或输出变量具有高斯分布的算法时才相关。
  
  回复
Deepak Mongia 2020年11月20日上午6:41 #

非常有帮助 Jason！直接明了，即取即用。

回复
- Jason Brownlee 2020年11月20日上午6:48 #
  
  不客气。
  
  回复
Borjakas 2021年1月30日上午3:47 #

感谢这篇有用的文章！

只是一个小建议
您认为在 Anderson 的示例中，是否可以将“cv”变量用于比较“if result.statistic < cv”而不是“if result.statistic < result.critical_values[i]:”？

回复
- Jason Brownlee 2021年1月30日上午6:38 #
  
  谢谢。
  
  回复
Henry Jacob 2021年4月16日下午3:54 #

嗨 Jason，
出色的工作，我很感激。
你为什么要在 Anderson Darling 测试中提到一个变量“p = 0”？

回复
- Jason Brownlee 2021年4月17日上午6:07 #
  
  我有吗？
  
  回复
Steven P. 2021年6月9日上午3:39 #

万一其他人遇到这个问题（得到 p 值为 0.000 似乎很奇怪），请调整您的打印语句，以便能够包含更多小数点。（例如，一种快速简便的方法是像这样更改“ print(‘Statistics=%.3f, p=%.10f’ % (stat, p)) ”。）

回复
- Jason Brownlee 2021年6月9日上午5:46 #
  
  好建议！
  
  回复
Aashish Rana 2021年11月26日下午10:59 #

学到了很多
谢谢 jason
你的博客是块宝藏

回复
- Adrian Tam 2021年11月29日上午8:37 #
  
  谢谢。很高兴你喜欢。
  
  回复
Hamzah 2022年3月13日上午2:40 #

我是一名来自也门的博士生，也是您的帖子的追随者，我真的不知道该如何感谢您。非常感谢您的时间和努力以及分享您的知识。

回复
- James Carmichael 2022年3月13日下午1:16 #
  
  Hamzah，反馈和支持非常出色！
  
  您可以通过几种方式回馈并支持我和这个网站。
  
  1. 传播消息
  
  口耳相传仍然非常重要。
  
  在社交媒体上分享有关机器学习精通的帖子。
  
  例如
  
  我非常喜欢 https://machinelearning.org.cn 上的机器学习教程
  
  2. 购买电子书
  
  我关于应用机器学习和深度学习的最佳建议都收录在我的电子书中。
  
  它们旨在帮助您以我所知道的最快方式学习并获得结果。
  
  所有电子书销售直接资助并支持我继续在这个网站上的工作和创建新的教程。
  
  探索电子书目录
  3. 捐款或成为赞助人
  
  如果您想在经济上支持这个网站但买不起电子书，那么请考虑一次性捐款。
  
  可以把它想象成给我买杯咖啡或在小费罐里加几美元。积少成多。
  
  您也可以选择成为赞助人并每月捐赠少量金额。
  
  了解如何捐款或成为赞助人
  谢谢！
  
  没有像您这样慷慨的读者的支持，这个网站将不复存在！
  
  回复

导航

Python 正态性检验简明入门

教程概述

需要机器学习统计学方面的帮助吗？

正态性假设

测试数据集

视觉正态性检查

直方图

分位数-分位数图

统计正态性检验

检验的解释

夏皮罗-威尔克检验 (Shapiro-Wilk Test)

D’Agostino’s K^2 检验

安德森-达令检验 (Anderson-Darling Test)

应该使用哪种检验？

硬性失败

软性失败

扩展

进一步阅读

API

文章

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

128 条对《Python 正态性检验入门指南》的回复

留下回复点击此处取消回复。

导航

教程概述

需要机器学习统计学方面的帮助吗？

正态性假设

测试数据集

视觉正态性检查

直方图

分位数-分位数图

统计正态性检验

检验的解释

夏皮罗-威尔克检验 (Shapiro-Wilk Test)

D’Agostino’s K^2 检验

安德森-达令检验 (Anderson-Darling Test)

应该使用哪种检验？

硬性失败

软性失败

扩展

进一步阅读

API

文章

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

128 条对《Python 正态性检验入门指南》的回复

留下回复 点击此处取消回复。

留下回复点击此处取消回复。