粒子群优化算法简明介绍

粒子群优化（PSO）是一种受生物启发而来的算法，它是一种在解空间中搜索最优解的简单算法。它与其他优化算法的不同之处在于，只需要目标函数，而不依赖于目标函数的梯度或任何微分形式。它还具有很少的超参数。

在本教程中，您将了解 PSO 的基本原理及其算法，并通过一个示例。完成本教程后，您将了解

• 什么是粒子群以及它们在 PSO 算法下的行为
• PSO 可以解决哪些类型的优化问题
• 如何使用粒子群优化解决问题
• PSO 算法有哪些变体

开始您的项目，阅读我的新书《机器学习优化》，其中包含分步教程和所有示例的Python源代码文件。

粒子群

粒子群优化由 Kennedy 和 Eberhart 于 1995 年提出。正如原始论文中所述，社会生物学家认为一群鱼或一群鸟类协同行动“可以从所有其他成员的经验中获益”。换句话说，例如，一只鸟在随机飞行和觅食时，群体中的所有鸟都可以分享它们的发现，并帮助整个群体获得最佳的捕猎成果。

粒子群优化。
照片由 Don DeBold 提供，部分权利保留。

虽然我们可以模拟鸟群的运动，但我们也可以想象每只鸟都在帮助我们在高维解空间中寻找最优解，而鸟群找到的最佳解就是该空间中的最佳解。这是一种启发式解决方案，因为我们永远无法证明能找到真正的全局最优解，而且通常也找不到。然而，我们经常发现 PSO 找到的解非常接近全局最优解。

示例优化问题

PSO 最适合用于寻找定义在多维向量空间上的函数的最大值或最小值。假设我们有一个函数 $f(X)$，它从向量参数 $X$（例如平面上的坐标 $(x,y)$）产生一个实数值，并且 $X$ 可以取空间中的几乎任何值（例如，$f(X)$ 是海拔高度，我们可以在平面上的任何点找到一个值），那么我们就可以应用 PSO。PSO 算法将返回它找到的产生最小 $f(X)$ 的参数 $X$。

让我们从以下函数开始

$$
f(x,y) = (x-3.14)^2 + (y-2.72)^2 + \sin(3x+1.41) + \sin(4y-1.73)
$$

f(x,y) 的绘图

正如我们在上面的图中所看到的，这个函数看起来像一个弯曲的蛋盒。它不是一个凸函数，因此很难找到它的最小值，因为找到的局部最小值不一定是全局最小值。

那么，我们如何找到这个函数中的最小点呢？当然，我们可以采用穷举搜索：如果我们检查平面上每个点的 $f(x,y)$ 值，就可以找到最小点。或者，如果我们认为搜索每个点成本太高，我们可以随机在平面上找一些样本点，看看哪个点在 $f(x,y)$ 上给出的值最低。然而，我们还注意到从 $f(x,y)$ 的形状来看，如果我们找到一个 $f(x,y)$ 值较小的点，那么在其附近更容易找到一个更小的值。

粒子群优化就是这样做的。与寻找食物的鸟群类似，我们从平面上的若干个随机点（称为粒子）开始，让它们以随机方向寻找最小点。在每一步，每个粒子都应该在其找到的最小点附近以及整个粒子群找到的最小点附近进行搜索。经过一定的迭代后，我们将函数的最小点视为该粒子群探索过的最小点。

算法细节

假设我们有 $P$ 个粒子，并将粒子 $i$ 在迭代 $t$ 的位置表示为 $X^i(t)$。在上面的例子中，我们将其表示为坐标 $X^i(t) = (x^i(t), y^i(t))$。除了位置之外，我们还为每个粒子定义了一个速度，表示为 $V^i(t)=(v_x^i(t), v_y^i(t))$。在下一次迭代中，每个粒子的位置将按以下规则更新：
$$
X^i(t+1) = X^i(t)+V^i(t+1)
$$
或者，等效地：
$$
\begin{aligned}
x^i(t+1) &= x^i(t) + v_x^i(t+1) \\
y^i(t+1) &= y^i(t) + v_y^i(t+1)
\end{aligned}
$$
同时，速度也将根据以下规则更新：
$$
V^i(t+1) =
w V^i(t) + c_1r_1(pbest^i – X^i(t)) + c_2r_2(gbest – X^i(t))
$$
其中 $r_1$ 和 $r_2$ 是介于 0 和 1 之间的随机数，$w$、$c_1$ 和 $c_2$ 是 PSO 算法的参数，而 $pbest^i$ 是粒子 $i$ 迄今为止探索到的使 $f(X)$ 值达到最佳的位置，而 $gbest$ 是整个粒子群迄今为止探索到的使 $f(X)$ 值达到最佳的位置。

请注意，$pbest^i$ 和 $X^i(t)$ 是两个位置向量，差值 $pbest^i – X^i(t)$ 是向量减法。将此差值加到原始速度 $V^i(t)$ 上是为了将粒子带回到 $pbest^i$ 的位置。对于差值 $gbest – X^i(t)$ 也是类似的。

向量减法。
图由 Benjamin D. Esham 提供，属于公共领域。

我们将参数 $w$ 称为惯性权重常数。它介于 0 和 1 之间，决定了粒子应该在多大程度上保持其先前的速度（即搜索的速度和方向）。参数 $c_1$ 和 $c_2$ 分别称为认知和群体系数。它们控制了粒子自身搜索结果的细化程度与群体搜索结果的识别程度之间的权重。我们可以认为这些参数控制了探索和利用之间的权衡。

在每次迭代中，位置 $pbest^i$ 和 $gbest$ 都会更新，以反映迄今为止找到的最佳位置。

该算法与其它优化算法不同的一点是，它不依赖于目标函数的梯度。例如，在梯度下降法中，我们通过将 $X$ 向 $-\nabla f(X)$ 的方向移动来寻找函数 $f(X)$ 的最小值，因为那是函数下降最快的方向。对于当前位置为 $X$ 的任何粒子，其移动方式不取决于“下坡”的方向，而仅取决于 $pbest$ 和 $gbest$ 的位置。这使得 PSO 特别适合于区分 $f(X)$ 困难的情况。

PSO 的另一个特点是它易于并行化。由于我们操纵多个粒子来寻找最优解，每个粒子都可以并行更新，我们只需要每迭代一次收集一次 $gbest$ 的更新值。这使得 map-reduce 架构成为实现 PSO 的理想选择。

实现

在这里，我们展示了如何实现 PSO 来寻找最优解。

对于上面展示的相同函数，我们可以先将其定义为一个 Python 函数，并在等高线图中显示它。

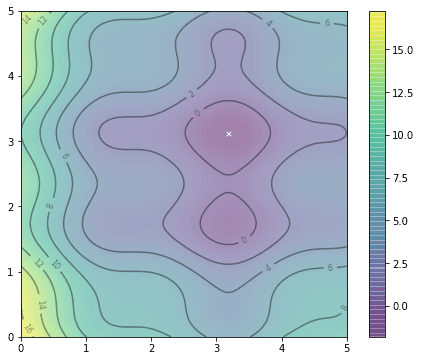
f(x,y) 的等高线图

我们在区域 $0\le x,y\le 5$ 内绘制了函数 $f(x,y)$。我们可以创建 20 个粒子，在区域内随机位置生成，并设置均值为 0、标准差为 0.1 的正态分布采样的随机速度，如下所示：

我们可以将它们的位置显示在同一张等高线图上。

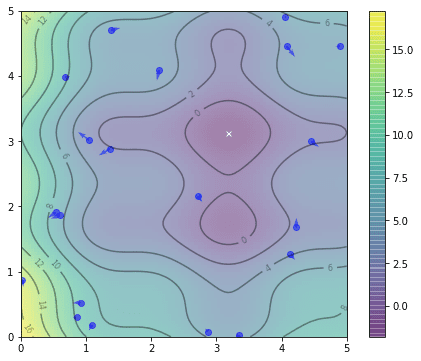
粒子的初始位置

由此，我们已经可以找到 $gbest$ 作为所有粒子迄今为止找到的最佳位置。由于粒子还没有进行任何探索，它们当前的位置也是它们的 $pbest^i$。

向量 `pbest_obj` 是每个粒子找到的目标函数值的最佳值。类似地，`gbest_obj` 是整个粒子群迄今为止找到的目标函数值的最佳标量值。由于我们将其设置为一个最小化问题，因此我们在此使用了 `min()` 和 `argmin()` 函数。下面用星号标记了 `gbest` 的位置。

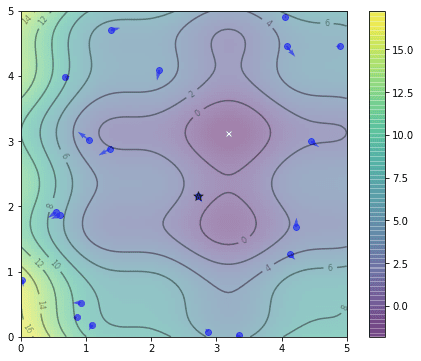
gbest 的位置用星号标记

让我们设置 $c_1=c_2=0.1$ 和 $w=0.8$。然后，我们可以根据上面提到的公式更新位置和速度，之后再更新 $pbest^i$ 和 $gbest$。

第一次迭代后的位置如下。我们用黑点标记每个粒子的最佳位置，以区别于它们当前的蓝色位置。

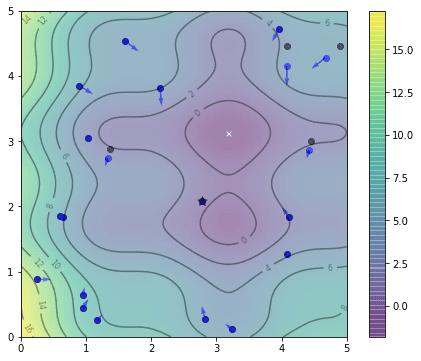
一次迭代后粒子的位置

我们可以多次重复上述代码段，看看粒子是如何探索的。这是第二次迭代后的结果：

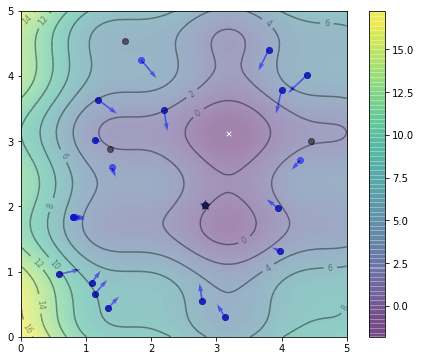
两次迭代后粒子的位置

这是第五次迭代后的结果，注意 $gbest$ 的位置（用星号表示）发生了变化。

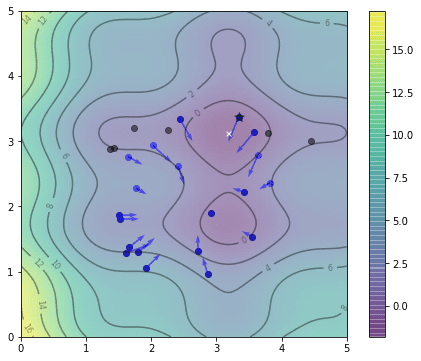
五次迭代后粒子的位置

这是第 20 次迭代后的结果，我们已经非常接近最优解了。

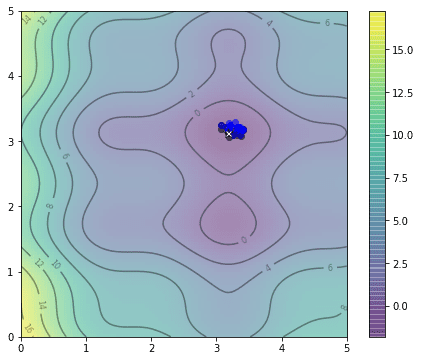
二十次迭代后粒子的位置

这是显示算法进程中如何找到最优解决方案的动画。看看是否能找到与鸟群运动的相似之处。

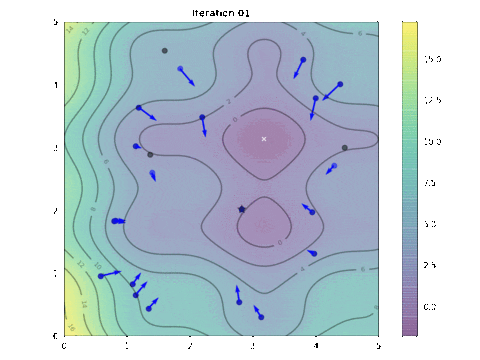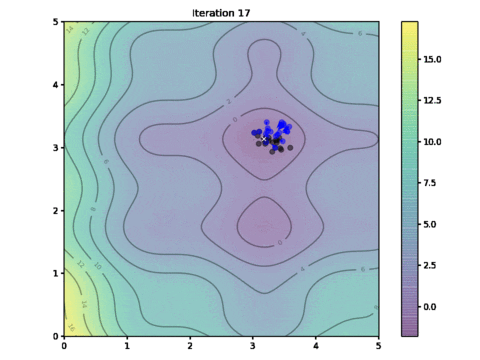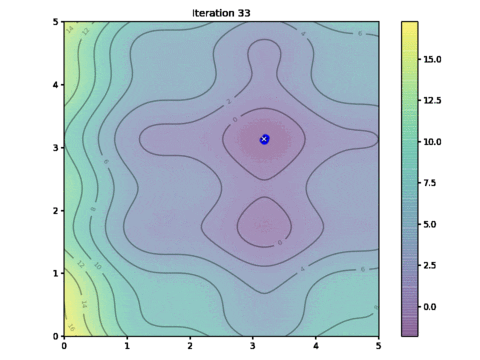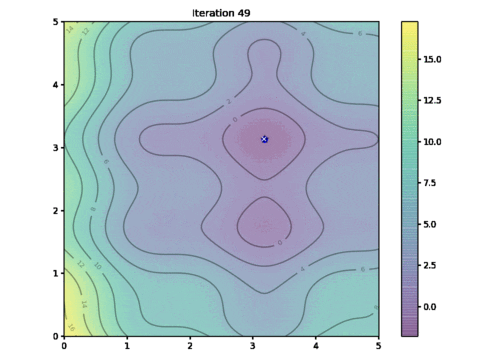
粒子运动的动画

那么我们的解决方案有多接近呢？在这个特定的例子中，我们通过穷举搜索找到的全局最小值位于坐标 $(3.182,3.131)$，而上面 PSO 算法找到的解决方案位于 $(3.185,3.130)$。

变体

正如我们上面提到的，所有 PSO 算法大部分是相同的。在上面的例子中，我们将 PSO 设置为在固定数量的迭代中运行。可以很容易地将迭代次数设置为动态响应进度。例如，我们可以设置当全局最佳解 $gbest$ 在一定次数的迭代中没有更新时停止。

PSO 的研究主要集中在如何确定超参数 $w$、$c_1$ 和 $c_2$，或者如何随着算法的进展改变它们的值。例如，有人提出将惯性权重线性递减。也有人提出使认知系数 $c_1$ 递减，同时使群体系数 $c_2$ 递增，以便在开始时进行更多探索，在结束时进行更多利用。有关示例，请参阅 Shi 和 Eberhart (1998) 以及 Eberhart 和 Shi (2000)。

完整示例

从上面的代码很容易看出我们如何将其更改为求解更高维的目标函数，或者从最小化切换到最大化。以下是求解上面提出的函数 $f(x,y)$ 的最小点以及生成绘图动画的代码的完整示例。

进一步阅读

这些是提出粒子群优化算法的原始论文，以及关于调整其超参数的早期研究

• Kennedy J. and Eberhart R. C. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks; Institute of Electrical and Electronics Engineers. Vol. 4. 1995. pp. 1942–1948. DOI: 10.1109/ICNN.1995.488968
• Eberhart R. C. and Shi Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation (CEC ‘00). Vol. 1. 2000. pp. 84–88. DOI: 10.1109/CEC.2000.870279
• Shi Y. and Eberhart R. A modified particle swarm optimizer. In Proceedings of the IEEE International Conferences on Evolutionary Computation, 1998. pp. 69–73. DOI: 10.1109/ICEC.1998.699146

总结

在本教程中我们学习了

• 粒子群优化是如何工作的
• 如何实现 PSO 算法
• 算法的一些可能的变体

由于粒子群优化算法没有太多的超参数，并且对目标函数非常宽容，因此可以用来解决各种各样的问题。

掌握现代优化算法！

加深您对优化的理解

...只需几行python代码

在我的新电子书中探索如何实现
机器学习优化

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
梯度下降、遗传算法、爬山法、曲线拟合、RMSProp、Adam，以及更多...

将现代优化算法应用于
您的机器学习项目

查看内容