Transformer 模型中位置编码的温和介绍，第 1 部分

在语言中，词语的顺序及其在句子中的位置确实很重要。如果词语的顺序被打乱，整个句子的意思可能会改变。在实现 NLP 解决方案时，循环神经网络具有处理序列顺序的内置机制。然而，Transformer 模型不使用循环或卷积，并将每个数据点视为相互独立的。因此，显式地向模型添加位置信息，以保留句子中词语顺序的信息。位置编码是保持序列中对象顺序知识的方案。

在本教程中，我们将简化 Vaswani 等人撰写的这篇杰出论文 《Attention Is All You Need》中使用的符号。完成本教程后，您将了解

• 什么是位置编码，以及为什么它很重要
• Transformer 中的位置编码
• 使用 Python 和 NumPy 编写代码并可视化位置编码矩阵

用我的书 《用注意力构建 Transformer 模型》 启动您的项目。它提供了 自学教程 和 可运行的代码，指导您构建一个功能齐全的 Transformer 模型，该模型可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...

让我们开始吧。

Transformer 模型中位置编码的温和介绍
图片由 Muhammad Murtaza Ghani 在 Unsplash 上提供，保留部分权利

教程概述

本教程分为四个部分；它们是

1. 什么是位置编码
2. Transformer 中位置编码背后的数学原理
3. 使用 NumPy 实现位置编码矩阵
4. 理解和可视化位置编码矩阵

什么是位置编码？

位置编码描述了序列中实体的位置，从而为每个位置分配一个唯一的表示。在 Transformer 模型中，不使用单个数字（例如索引值）来表示项目位置的原因有很多。对于长序列，索引值可能会变得很大。如果您将索引值归一化到 0 到 1 之间，对于可变长度序列可能会产生问题，因为它们的归一化方式会不同。

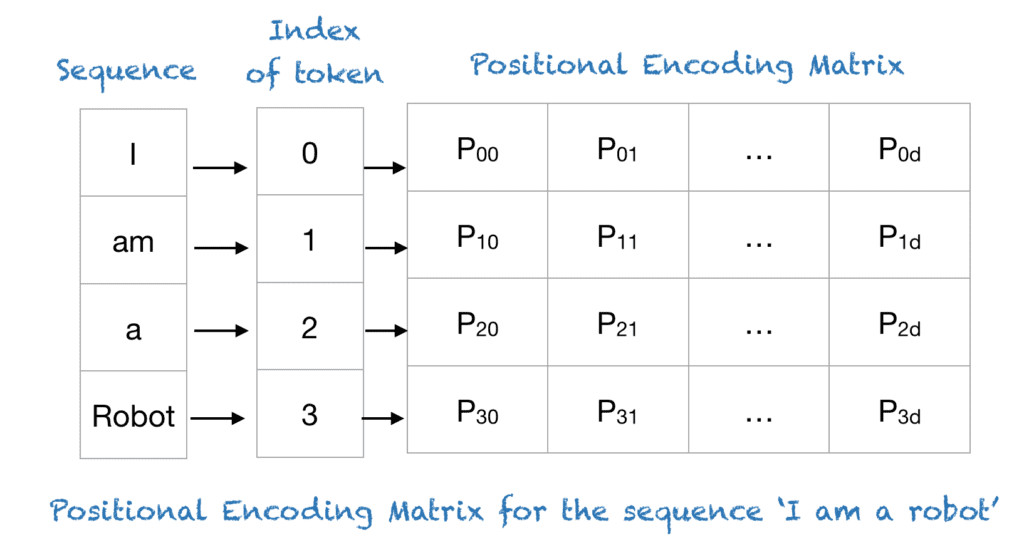
Transformer 使用一种智能的位置编码方案，其中每个位置/索引都被映射到一个向量。因此，位置编码层的输出是一个矩阵，矩阵的每一行代表序列中编码对象与其位置信息的总和。下图显示了一个仅编码位置信息的矩阵示例。

三角正弦函数的快速回顾

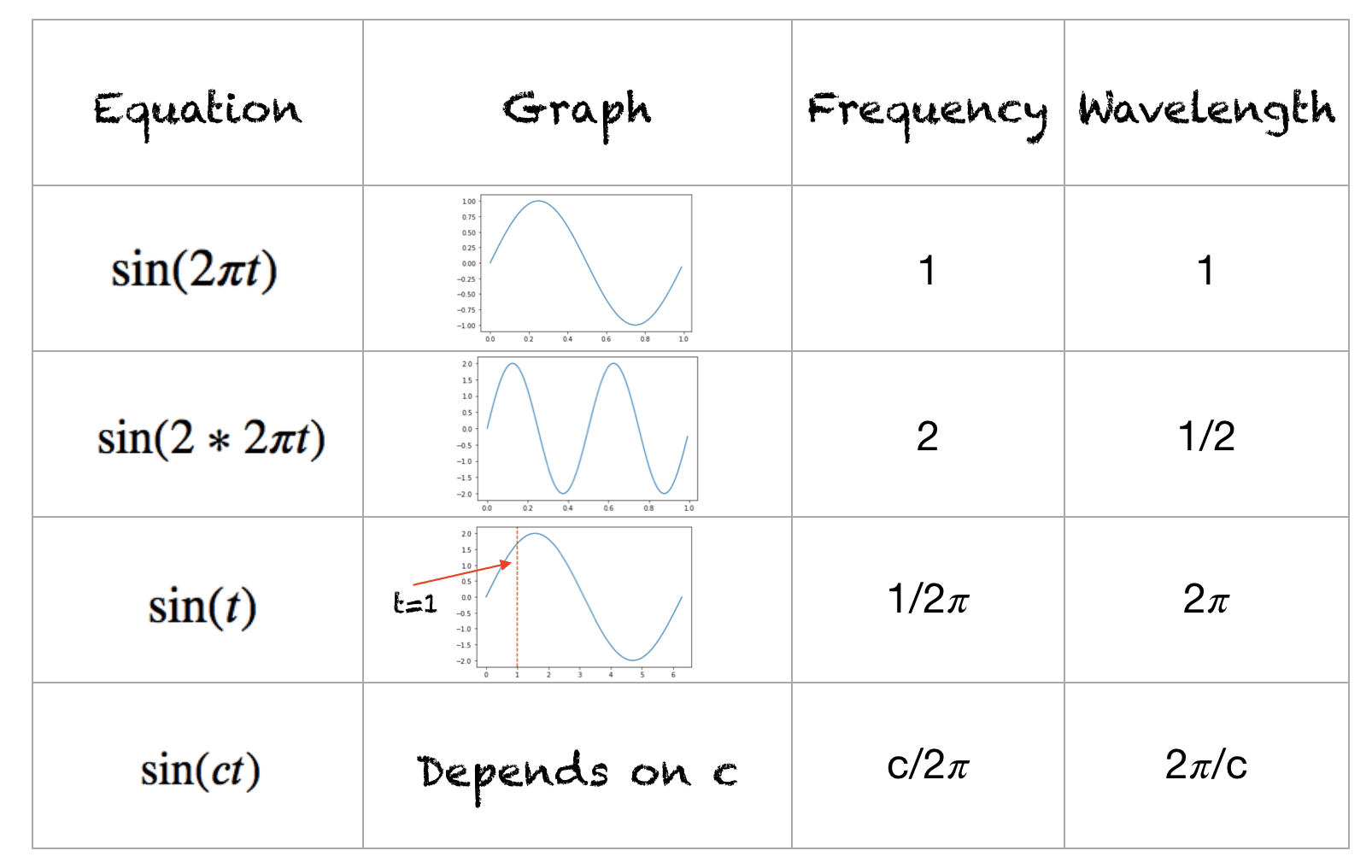
这是对正弦函数的快速回顾；您可以等效地使用余弦函数。函数的范围是 [-1,+1]。此波形的频率是每秒完成的周期数。波长是波形重复自身的距离。不同波形的波长和频率如下所示

Transformer 中的位置编码层

让我们直接深入探讨。假设您有一个长度为 $L$ 的输入序列，并且需要此序列中第 $k^{th}$ 个对象的位置。位置编码由不同频率的正弦和余弦函数给出

\begin{eqnarray}
P(k, 2i) &=& \sin\Big(\frac{k}{n^{2i/d}}\Big)\\
P(k, 2i+1) &=& \cos\Big(\frac{k}{n^{2i/d}}\Big)
\end{eqnarray}

这里：

$k$：输入序列中对象的位置，$0 \leq k < L/2$

$d$：输出嵌入空间的维度

$P(k, j)$：将输入序列中的位置 $k$ 映射到位置矩阵的索引 $(k,j)$ 的位置函数

$n$：《Attention Is All You Need》的作者设定为 10,000 的用户定义标量。

$i$：用于映射到列索引 $0 \leq i < d/2$，其中单个 $i$ 值映射到正弦和余弦函数

在上述表达式中，您可以看到偶数位置对应于正弦函数，奇数位置对应于余弦函数。

例如

为了理解上述表达式，让我们以短语“我是一个机器人”为例，其中 n=100 且 d=4。下表显示了此短语的位置编码矩阵。实际上，对于任何 n=100 且 d=4 的四个字母短语，位置编码矩阵都是相同的。

从头开始编码位置编码矩阵

这是一个使用 NumPy 实现位置编码的简短 Python 代码。代码经过简化，以便更容易理解位置编码。

为了理解位置编码，我们首先来看看当 n=10,000 且 d=512 时，不同位置的正弦波。

Python

def plotSinusoid(k, d=512, n=10000): x = np.arange(0, 100, 1) denominator = np.power(n, 2*x/d) y = np.sin(k/denominator) plt.plot(x, y) plt.title('k = ' + str(k)) fig = plt.figure(figsize=(15, 4)) for i in range(4): plt.subplot(141 + i) plotSinusoid(i*4)

1 2 3 4 5 6 7 8 9 10 11

def plotSinusoid(k, d=512, n=10000):     x = np.arange(0, 100, 1)     denominator = np.power(n, 2*x/d)     y = np.sin(k/denominator)     plt.plot(x, y)     plt.title('k = ' + str(k))   fig = plt.figure(figsize=(15, 4))     for i in range(4):     plt.subplot(141 + i)     plotSinusoid(i*4)

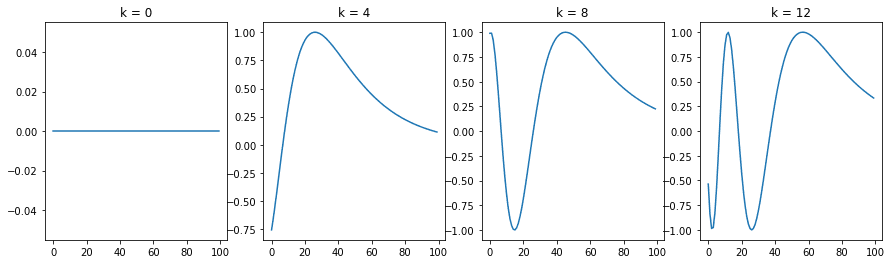
下图是上述代码的输出

不同位置索引的正弦波

您可以看到每个位置 $k$ 对应一个不同的正弦曲线，它将单个位置编码成一个向量。如果您仔细观察位置编码函数，您会发现对于固定的 $i$，波长由以下公式给出

$$
\lambda_{i} = 2 \pi n^{2i/d}
$$

因此，正弦波的波长形成一个几何级数，并从 $2\pi$ 变化到 $2\pi n$。位置编码方案具有许多优点。

1. 正弦和余弦函数的值在 [-1, 1] 范围内，这使得位置编码矩阵的值保持在归一化范围内。
2. 由于每个位置的正弦波都不同，因此您有一种独特的方式来编码每个位置。
3. 您有一种衡量或量化不同位置之间相似性的方法，因此能够编码词语的相对位置。

可视化位置矩阵

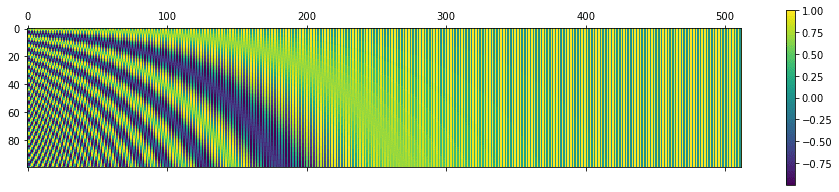
让我们可视化更大值的位置矩阵。使用 Python 的 `matplotlib` 库中的 `matshow()` 方法。将 n=10,000 设置为原始论文中所做的那样，您将获得以下结果

Python

P = getPositionEncoding(seq_len=100, d=512, n=10000) cax = plt.matshow(P) plt.gcf().colorbar(cax)

1 2 3

P = getPositionEncoding(seq_len=100, d=512, n=10000) cax = plt.matshow(P) plt.gcf().colorbar(cax)

位置编码矩阵，其中 n=10,000，d=512，序列长度=100

位置编码层的最终输出是什么？

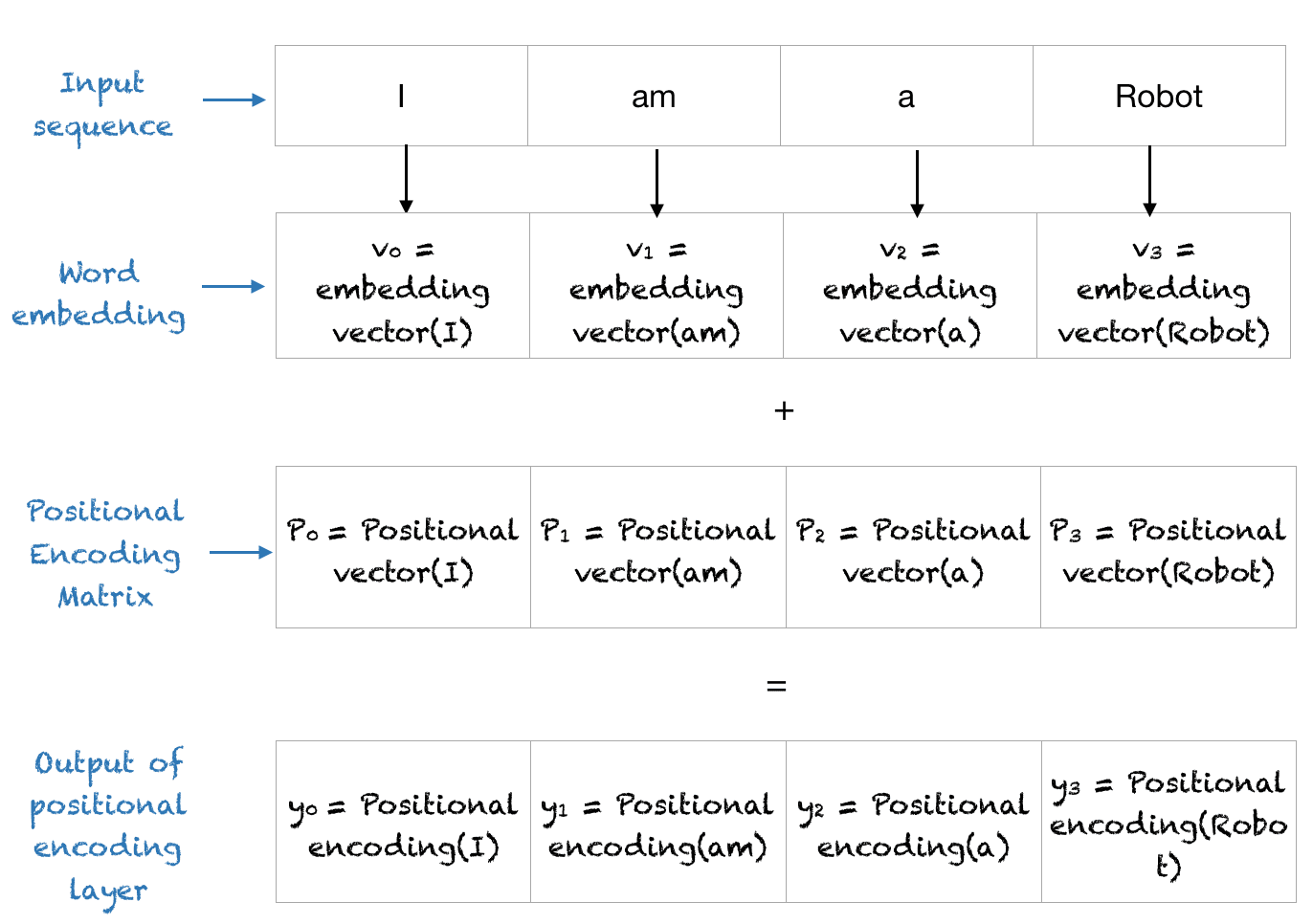
位置编码层将位置向量与词编码相加，并将此矩阵输出到后续层。整个过程如下所示。

Transformer 中的位置编码层

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 《自然语言处理的 Transformer》，作者 Denis Rothman。

论文

• 注意力就是你所需要的一切, 2017.

文章

• Transformer 注意力机制
• Transformer 模型
• 用于语言理解的 Transformer 模型

总结

在本教程中，您了解了 Transformer 中的位置编码。

具体来说，你学到了：

• 什么是位置编码，以及为什么需要它。
• 如何使用 NumPy 在 Python 中实现位置编码
• 如何可视化位置编码矩阵

您对本文讨论的位置编码有任何疑问吗？请在下面的评论中提出您的问题，我将尽力回答。

学习 Transformer 和注意力！

教您的深度学习模型阅读句子

...使用带有注意力的 Transformer 模型

在我的新电子书中探索如何实现
使用注意力机制构建 Transformer 模型

它提供了自学教程和可运行代码，指导您构建一个可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...

为理解人类语言提供神奇力量
您的项目

查看内容