泰勒级数简明入门
泰勒级数展开是一个非常棒的概念,不仅在数学世界中,而且在优化理论、函数逼近和机器学习中也同样如此。当需要估算函数在不同点的值时,它被广泛应用于数值计算。
在本教程中,你将了解泰勒级数以及如何使用其泰勒级数展开来近似函数在不同点的值。
完成本教程后,您将了解:
- 函数的泰勒级数展开
- 如何使用泰勒级数展开来近似函数
让我们开始吧。
教程概述
本教程分为3个部分;它们是
- 幂级数和泰勒级数
- 泰勒多项式
- 使用泰勒多项式进行函数逼近
什么是幂级数?
以下是一个以 x=a 为中心,常数系数为 c_0, c_1 等的幂级数。
什么是泰勒级数?
一个惊人的事实是,无限可微的函数可以生成一个称为泰勒级数的幂级数。假设我们有一个函数 f(x),并且 f(x) 在给定区间上具有所有阶的导数,那么由 f(x) 在 x=a 处生成的泰勒级数由以下公式给出:
上述表达式的第二行给出了第 k 个系数的值。
如果我们将 a=0,那么我们得到 f(x) 的麦克劳林级数展开。
想开始学习机器学习微积分吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
泰勒级数展开的例子
由 f(x) = 1/x 生成的泰勒级数可以通过首先对函数求导并找到第 k 阶导数的一般表达式来获得。
现在可以找到围绕不同点的泰勒级数。例如:
泰勒多项式
由 f(x) 在 x=a 处生成的 k 阶泰勒多项式由以下公式给出:
对于 f(x)=1/x 的例子,2 阶泰勒多项式由以下公式给出:
通过泰勒多项式进行逼近
我们可以使用泰勒多项式来近似函数在 x=a 点的值。多项式的阶数越高,多项式中的项越多,近似值就越接近函数在该点的实际值。
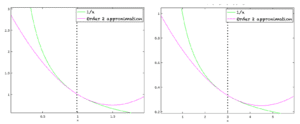
在下面的图中,函数 1/x 绘制在 x=1 点附近(左)和 x=3 点附近(右)。绿色线是实际函数 f(x)= 1/x。粉色线表示通过 2 阶多项式进行的近似。
更多泰勒级数的例子
我们来看函数 g(x) = e^x。注意到 g(x) 的 k 阶导数也是 g(x),g(x) 在 x=a 附近的展开式由以下公式给出:
因此,在 x=0 附近,g(x) 的级数展开式由以下公式给出(通过设置 a=0 获得):
为函数 e^x 在 x=0 附近生成的 k 阶多项式由以下公式给出:
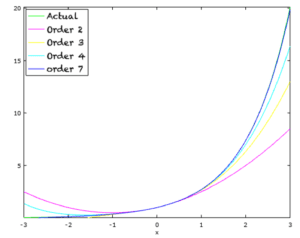
下面的图显示了估计 e^x 在 x=0 附近值的不同阶多项式。我们可以看到,当我们远离零点时,我们需要更多的项来更准确地近似 e^x。代表实际函数的绿色线隐藏在阶数为 7 的近似多项式的蓝色线后面。
机器学习中的泰勒级数
机器学习中寻找函数最优点的常用方法是牛顿法。牛顿法使用二阶多项式来近似函数在某一点的值。这类使用二阶导数的方法被称为二阶优化算法。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 牛顿法
- 二阶优化算法
如果您探索了这些扩展内容中的任何一个,我很想知道。请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
资源
- Jason Brownlee 关于机器学习微积分书籍的优秀资源
书籍
- Christopher M. Bishop 著《模式识别与机器学习》。
- Ian Goodfellow, Joshua Begio, Aaron Courville 著《深度学习》。
- 《托马斯微积分》,第14版,2017年。(基于George B. Thomas的原始著作,由Joel Hass, Christopher Heil, Maurice Weir修订)
- 《微积分》,第3版,2017年。(Gilbert Strang)
- 微积分,第 8 版,2015 年。(James Stewart)
总结
在本教程中,你了解了函数在某一点的泰勒级数展开。具体来说,你学到了:
- 幂级数和泰勒级数
- 泰勒多项式
- 如何使用泰勒多项式近似函数在某个值附近的值
你有什么问题吗?
请在下方评论中提出您的问题,我将尽力回答。

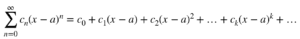
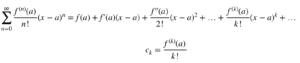
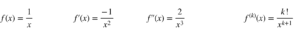
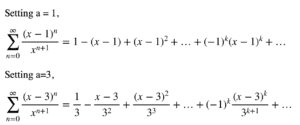
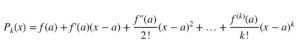
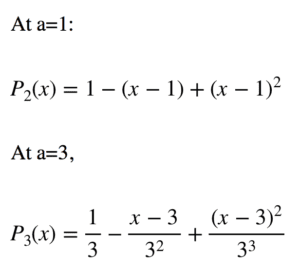
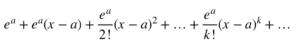
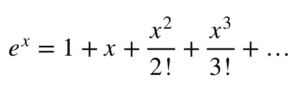
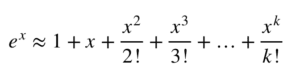






精彩的解释。直到现在我才理解泰勒级数的概念。
谢谢你。很高兴你喜欢。
解释方式对于初学者来说很容易理解。谢谢。
另外,请告诉我们你关于近似函数在特定值附近的应用(包含大量示例)的任何帖子/教程。
感谢您的宝贵反馈 Sarva!