简要介绍训练深度学习神经网络模型的挑战

深度学习神经网络学习将输入映射到输出的函数。

这是通过根据模型在训练数据集上产生的错误来更新网络权重来实现的。更新会不断减少此错误，直到找到足够好的模型或学习过程陷入停滞。

神经网络的训练过程是使用该技术最具挑战性的部分，也是迄今为止最耗时的部分，无论是配置过程所需的精力还是执行过程所需的计算复杂性。

在这篇文章中，您将了解为深度学习神经网络寻找模型参数的挑战。

阅读本文后，你将了解：

• 神经网络学习将输入映射到输出的函数，这可以概括为解决函数逼近问题。
• 与其他机器学习算法不同，神经网络的参数必须通过解决一个非凸优化问题来找到，该问题具有许多好的解决方案和许多具有误导性的好解决方案。
• 随机梯度下降算法用于解决优化问题，其中模型参数在每次迭代中使用反向传播算法进行更新。

用我的新书《更好的深度学习》来启动你的项目，书中包含分步教程和所有示例的 Python 源代码文件。

让我们开始吧。

简要介绍训练深度学习神经网络模型的挑战
图片由Miguel Discart拍摄，保留部分权利。

概述

本教程分为四个部分；它们是

1. 神经网络学习映射函数
2. 学习网络权重很困难
3. 导航误差表面
4. 学习算法的组成部分

神经网络学习映射函数

深度学习神经网络学习映射函数。

开发模型需要来自领域中的历史数据，这些数据用作训练数据。这些数据由来自领域的观测或示例组成，其中包含描述条件的输入元素和捕获观测含义的输出元素。

例如，输出为数量的问题通常被称为回归预测建模问题。而输出为标签的问题通常被称为分类预测建模问题。

神经网络模型利用这些示例学习如何将特定输入变量集映射到输出变量。它必须以这种方式进行，使这种映射在训练数据集上表现良好，同时也能在模型训练期间未见过的新示例上表现良好。这种在特定示例和新示例上都能良好工作的能力称为模型的泛化能力。

多层感知器只是一个将某些输入值集映射到输出值的数学函数。

——《深度学习》，第5页，2016年。

我们可以将输入变量和输出变量之间的关系描述为一个复杂的数学函数。对于一个给定的模型问题，我们必须相信存在一个真实的映射函数能够最好地将输入变量映射到输出变量，并且神经网络模型可以在近似真实的未知底层映射函数方面做得相当好。

前馈网络定义了一个映射，并学习了能够实现最佳函数逼近的参数值。

——《深度学习》，第168页，2016年。

因此，我们可以将神经网络解决的更广泛问题描述为“函数逼近”。它们通过给定训练数据集来学习近似未知的底层映射函数。它们通过在给定的我们设计的特定网络结构下学习权重和模型参数来实现这一点。

最好将前馈网络视为函数逼近机器，旨在实现统计泛化，偶尔从我们对大脑的了解中汲取一些见解，而不是将其视为大脑功能的模型。

——《深度学习》，第169页，2016年。

学习网络权重很困难

通常，寻找神经网络的参数很困难。

对于许多简单的机器学习算法，我们可以根据训练数据集计算出最优模型。

例如，我们可以使用线性代数来计算线性回归模型的特定系数和训练数据集，以最小化平方误差。

同样，我们可以使用优化算法，在寻找非线性算法（如逻辑回归或支持向量机）的最佳模型参数集时，提供收敛保证。

寻找许多机器学习算法的参数涉及解决凸优化问题：即一个碗状的误差表面，只有一个最佳解决方案。

深度学习神经网络并非如此。

我们既不能直接计算模型的最优权重集，也不能获得全局收敛保证来找到最优权重集。

应用于非凸损失函数的随机梯度下降没有 […] 收敛保证，并且对初始参数的值敏感。

——《深度学习》，第177页，2016年。

事实上，训练神经网络是使用该技术中最具挑战性的部分。

即使只是解决一个神经网络训练问题，也通常需要投入数天到数月的时间，动用数百台机器。

——《深度学习》，第274页，2016年。

神经网络中非线性激活函数的使用意味着我们为了找到模型参数而必须解决的优化问题是非凸的。

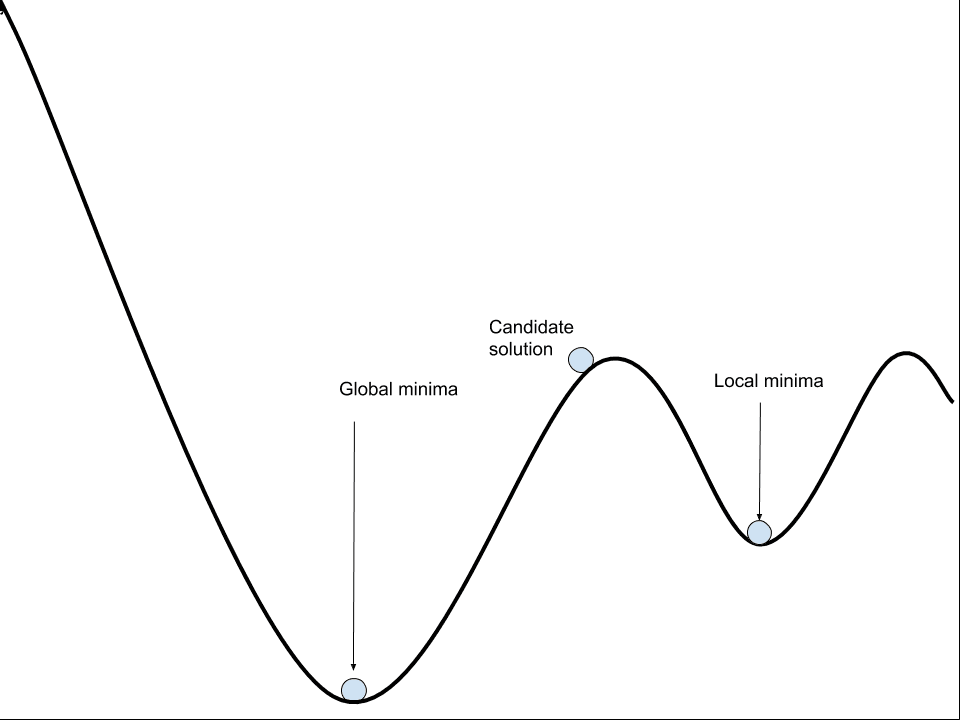
它不是一个简单的碗状，拥有一个我们保证能找到的最佳权重集。相反，它是一个山峰和山谷交错的景观，有许多好的和许多具有误导性的好的参数集我们可能会发现。

解决这种优化问题具有挑战性，尤其是因为误差表面包含许多局部最优、平坦区域和陡峭悬崖。

必须使用迭代过程来导航模型的非凸误差表面。一个天真地导航误差的算法很可能会被误导、迷失并最终陷入困境，导致模型性能不佳。

导航非凸误差表面

神经网络模型可以被认为是通过导航非凸误差表面来学习的。

一个具有特定权重集的模型可以在训练数据集上进行评估，所有训练数据集的平均误差可以被认为是模型的误差。模型权重的改变将导致模型误差的改变。因此，我们寻求一个能够导致模型误差较小的权重集。

这涉及重复评估模型和更新模型参数的步骤，以便沿着误差表面下降。这个过程会重复进行，直到找到一组足够好的参数，或者搜索过程陷入停滞。

这是一个搜索或优化过程，我们将以这种方式运行的优化算法称为梯度优化算法，因为它们天真地沿着误差梯度下降。它们计算成本高昂、速度慢，并且它们的经验行为意味着在实践中使用它们更像是艺术而非科学。

最常用于导航误差表面的算法称为随机梯度下降，简称SGD。

几乎所有的深度学习都由一个非常重要的算法驱动：随机梯度下降，或简称SGD。

——《深度学习》，第151页，2016年。

其他为非凸优化问题设计的全局优化算法也可以使用，例如遗传算法，但随机梯度下降更有效，因为它通过一个名为反向传播的算法，专门使用梯度信息来更新模型权重。

[反向传播]描述了一种通过巧妙应用导数链式法则来计算网络训练误差对权重的导数的方法。

——《神经网络锻造：前馈人工神经网络中的监督学习》，第49页，1999年。

反向传播指的是微积分中的一种技术，用于计算特定模型参数的模型误差的导数（例如斜率或梯度），从而允许更新模型权重以沿着梯度下降。因此，用于训练神经网络的算法也常被简称为反向传播。

实际上，反向传播仅指计算梯度的方法，而另一个算法，例如随机梯度下降，则用于利用此梯度进行学习。

——《深度学习》，第204页，2016年。

随机梯度下降可用于寻找其他机器学习算法（如线性回归）的参数，当处理非常大的数据集时使用，尽管如果有足够的资源，基于凸的优化算法效率会显著更高。

学习算法的组成部分

使用随机梯度下降和反向传播训练深度学习神经网络模型涉及选择许多组件和超参数。在本节中，我们将逐一介绍。

必须选择一个误差函数，通常称为目标函数、成本函数或损失函数。通常选择一种特定的用于推断的概率框架，称为最大似然。在此框架下，常用的损失函数是用于分类问题的交叉熵和用于回归问题的均方误差。

• 损失函数。用于估计模型在训练数据集示例上具有特定权重集的性能的函数。

搜索或优化过程需要一个起点来开始模型更新。起点由初始模型参数或权重定义。因为误差表面是非凸的，所以优化算法对初始起点敏感。因此，选择小的随机值作为初始模型权重，尽管可以使用不同的技术来选择这些值的尺度和分布。这些技术被称为“权重初始化”方法。

• 权重初始化。在训练过程开始时，将初始小的随机值分配给模型权重的过程。

更新模型时，必须使用训练数据集中的多个示例来计算模型误差，通常简称为“损失”。可以使用训练数据集中的所有示例，这可能适用于较小的数据集。另外，可以使用单个示例，这可能适用于示例流式传输或数据经常变化的问题。可以采用混合方法，选择训练数据集中的示例数量并用于估计误差梯度。示例数量的选择称为批次大小。

• 批次大小。在更新模型参数之前，用于估计误差梯度的示例数量。

一旦误差梯度被估计，就可以计算误差的导数并用于更新每个参数。训练数据集和误差梯度估计中可能存在统计噪声。此外，模型的深度（层数）以及模型参数分别更新的事实意味着，很难精确计算每个模型参数需要改变多少才能最好地使整个模型沿着误差梯度下降。

相反，每次迭代只执行一小部分权重更新。一个名为“学习率”的超参数控制着模型权重更新的幅度，进而控制着模型在训练数据集上的学习速度。

• 学习率：每个模型参数在学习算法的每个周期中更新的量。

训练过程必须重复多次，直到发现一组良好或足够好的模型参数。该过程的总迭代次数受训练数据集的完整遍历次数限制，之后训练过程终止。这称为训练“周期”数。

• 周期。训练过程终止前，完整遍历训练数据集的次数。

学习算法有许多扩展，尽管这五个超参数通常控制深度学习神经网络的学习算法。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

• 深度学习, 2016.
• 《神经网络精工：前馈人工神经网络中的监督学习》, 1999.
• 《用于模式识别的神经网络》, 1995.

总结

在这篇文章中，您发现了为深度学习神经网络寻找模型参数的挑战。

具体来说，你学到了：

• 神经网络学习将输入映射到输出的函数，这可以概括为解决函数逼近问题。
• 与其他机器学习算法不同，神经网络的参数必须通过解决一个非凸优化问题来找到，该问题具有许多好的解决方案和许多具有误导性的好解决方案。
• 随机梯度下降算法用于解决优化问题，其中模型参数在每次迭代中使用反向传播算法进行更新。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

今天就开发更好的深度学习模型！

更快地训练，减少过拟合，以及集成方法

...只需几行python代码

在我的新电子书中探索如何实现
更好的深度学习

它提供关于以下主题的自学教程：
权重衰减、批量归一化、dropout、模型堆叠等等...

为你的项目带来更好的深度学习！

跳过学术理论。只看结果。

查看内容