我们直觉上认为更多的观察量会更好。
这与如果我们收集更多数据,我们的数据样本将更能代表问题领域这一理念背后的直觉相同。
统计学和概率学中有一条定理支持这种直觉,它是这两个领域的基石,并对应用机器学习有重要影响。这条定理的名字叫做大数定律。
在本教程中,您将了解大数定律及其在应用机器学习中的重要性。
完成本教程后,您将了解:
- 大数定律支持这样的直觉:随着样本量的增加,样本将更好地代表总体。
- 如何在Python中开发一个小型示例来演示样本量增加如何减少误差。
- 大数定律对于理解机器学习中训练数据集、测试数据集的选择以及模型性能的评估至关重要。
启动您的项目,阅读我的新书《机器学习统计学》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

机器学习中的大数定律入门简介
照片由 Raheel Shahid 拍摄,部分权利保留。
教程概述
本教程分为3个部分;它们是
- 大数定律
- 实例演示
- 在机器学习中的应用
需要机器学习统计学方面的帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
大数定律
大数定律是来自概率和统计学的一条定理,它表明重复实验多次的平均结果将更好地近似真实或预期的潜在结果。
大数定律解释了为什么赌场总是能长期赚钱。
— 第 79 页,《赤裸统计学:揭开数据之惑》,2014年。
我们可以将一次实验的尝试视为一次观察。实验的独立重复将进行多次尝试并产生多个观察。实验的所有样本观察都是从理想化的观察总体中提取的。
- 观察:实验一次尝试的结果。
- 样本:从单独的独立尝试中收集的结果组。
- 总体:可以从一次实验中看到的可能观察的集合。
使用统计学中的这些术语,我们可以说,随着样本量的增加,样本的平均值将更好地近似总体中的平均值或期望值。当样本量趋于无穷大时,样本均值将收敛于总体均值。
……概率的一个重要成果,即大数定律。这条定理指出,大样本的均值接近分布的均值。
— 第 76 页,《所有统计学:统计推断简明教程》,2004年。
这是统计学和概率学以及应用机器学习的一个重要理论发现。
独立同分布
明确样本中的观察必须是独立的,这一点很重要。
这意味着实验以相同的方式进行,并且不依赖于任何其他实验的结果。这在计算机中通常是合理且容易实现的,但在其他地方可能很困难(例如,如何实现骰子完全随机的滚动?)。
在统计学中,这种期望被称为“独立同分布”,简称 IID、iid 或 i.i.d.。这是为了确保样本确实是从相同的潜在总体分布中提取的。
均值回归
大数定律帮助我们理解为什么我们不能孤立地信任实验的单次观察。
我们预期单次结果或小样本的平均结果很可能接近中心趋势,即总体分布的均值。它可能不接近;事实上,它可能非常奇怪或不太可能。
该定律提醒我们在开始推断结果含义之前,应重复实验以形成一个大型且具有代表性的观察样本。
随着样本量的增加,样本的发现或均值将回归到总体均值,回归到真实的潜在期望值。这被称为 均值回归,有时也称为均值复归。
这就是为什么我们必须对来自小样本(称为小n)的推断持怀疑态度。
真正大数定律
与均值回归相关的是 真正大数定律。
这是这样一种观念:当我们开始调查或处理海量的观察样本时,我们会增加看到奇怪现象的可能性。通过拥有如此多的潜在总体分布样本,样本将包含一些天文数字般罕见的事件。
同样,我们必须警惕不要从单个案例中进行推断。
在运行查询和处理大数据时,考虑这一点尤其重要。
实例演示
我们可以通过一个小的工作示例来演示大数定律。
首先,我们可以设计一个理想化的潜在分布。我们将使用均值为 50、标准差为 5 的高斯分布。因此,此总体的期望值或均值为 50。
以下是一些生成此理想化分布图的代码。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 理想化总体分布 from numpy import arange from matplotlib import pyplot from scipy.stats import norm # 绘图的x轴 xaxis = arange(30, 70, 1) # 绘图的y轴 yaxis = norm.pdf(xaxis, 50, 5) # 绘制理想总体 pyplot.plot(xaxis, yaxis) pyplot.show() |
运行代码会生成所设计的总体图,具有熟悉的钟形曲线。
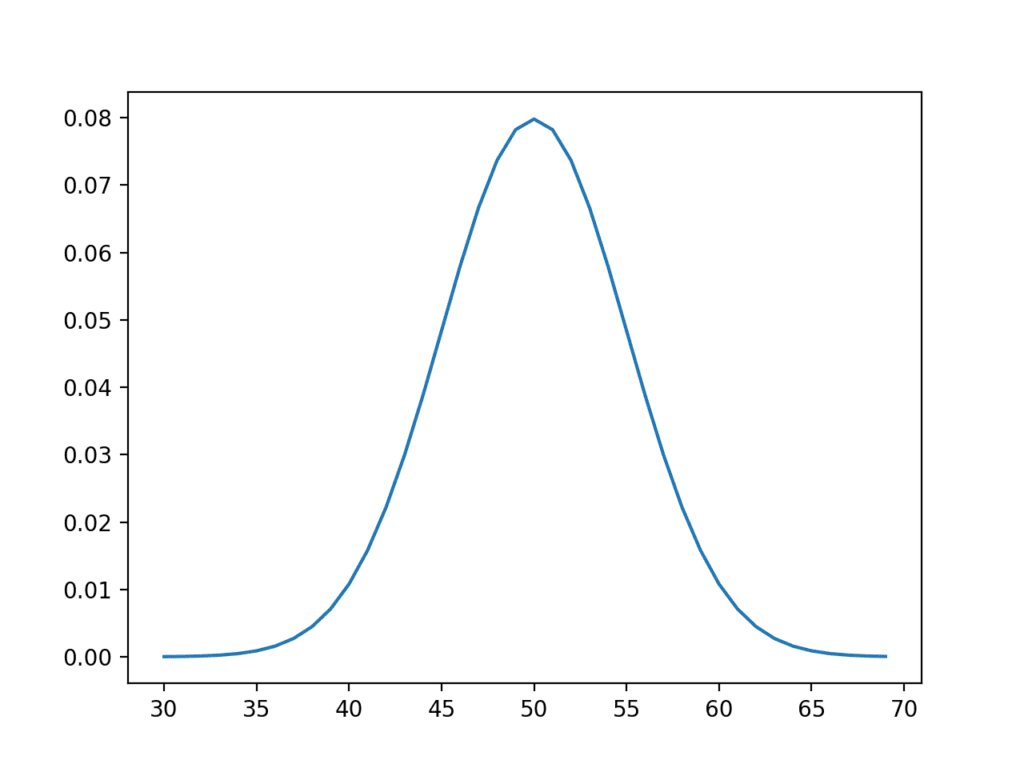
理想化潜在总体分布
现在,我们可以假装忘记我们所知道的关于总体的一切,并从总体中进行独立的随机抽样。
我们可以创建不同大小的样本并计算均值。根据我们的直觉和大数定律,我们预计随着样本量的增加,样本均值将更好地近似总体均值。
下面的示例计算不同大小的样本,然后打印样本均值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 演示大数定律 from numpy.random import seed from numpy.random import randn from numpy import mean from numpy import array from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 样本大小 sizes = [10, 100, 500, 1000, 10000] # 生成不同大小的样本并计算它们的均值 means = [mean(5 * randn(size) + 50) for size in sizes] print(means) # 绘制样本均值误差与样本量的关系图 pyplot.scatter(sizes, array(means)-50) pyplot.show() |
运行示例首先打印每个样本的均值。
我们可以看到,随着样本量的增加,样本均值越来越接近 50.0 的一个松散趋势。
同时也要注意,这个样本均值样本也必须服从大数定律。例如,偶然地,您可能会通过小样本的均值得到一个非常准确的总体均值估计。
|
1 |
[49.5142955459695, 50.371593294898695, 50.2919653390298, 50.1521157689338, 50.03955033528776] |
该示例还创建了一个图,将样本大小与样本均值与总体均值之间的误差进行比较。通常,我们可以看到较大的样本量误差较小,并且我们预计这种趋势平均而言会持续下去。
我们还可以看到一些样本均值高估,一些样本均值低估。不要陷入低估会落在一边或另一边的陷阱。
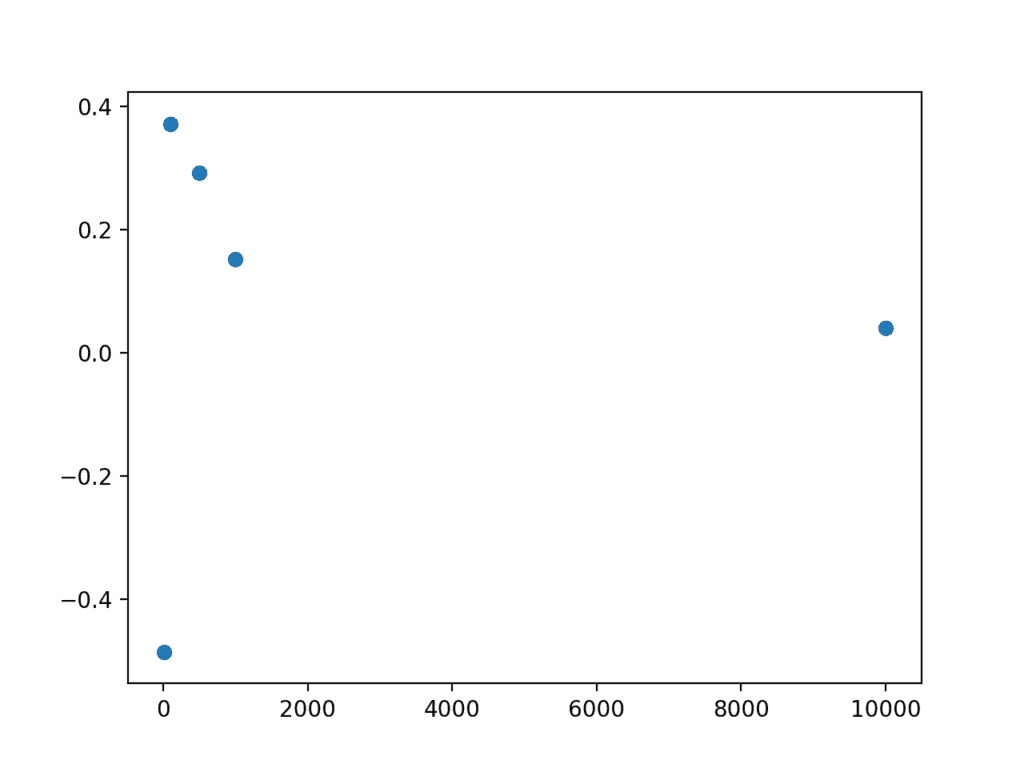
样本量与误差的散点图
在机器学习中的应用
大数定律对应用机器学习有重要影响。
让我们花点时间重点介绍其中一些影响。
训练数据
用于训练模型的数据必须能代表来自该领域的所有观察。
这确实意味着它必须包含足够的信息才能泛化到真实未知的潜在总体分布。
对于模型的单个输入变量,这很容易概念化,但在您拥有多个输入变量时同样重要。输入变量之间将存在未知的关系或依赖关系,并且总的来说,输入数据将代表一个多元分布,从中将提取观察结果来组成您的训练样本。
在数据收集、数据清理和数据准备过程中请牢记这一点。
您可能选择排除潜在总体的某些部分,通过为观察值设置硬限制(例如,用于异常值),因为您预计数据过于稀疏而无法有效建模。
测试数据
对训练数据集的考虑也必须给予测试数据集。
这通常会被 80/20 的训练/测试数据分割或 10 折交叉验证的盲目使用所忽略,即使在可用数据的 1/10 大小可能不能很好地代表问题领域观察的数据集上也是如此。
模型技能评估
在呈现模型在未见过数据上的估计技能时,请考虑大数定律。
它为不简单地根据单个训练/测试评估的技能分数来报告或继续使用模型提供了依据。
它强调了开发一系列给定模型的多个独立(或接近独立)评估样本的必要性,以便样本报告的平均技能能够足够准确地估计总体均值。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 请为大数定律适用的另外两个机器学习领域集思广益。
- 找到五个研究论文,您对结果持怀疑态度,考虑到大数定律。
- 开发您自己的理想分布和样本,并绘制样本量与样本均值误差之间的关系图。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 《赤裸统计学:摆脱数据恐惧》, 2014.
- 统计学大全:统计推断简明教程, 2004.
API
文章
总结
在本教程中,您了解了大数定律及其在应用机器学习中的重要性。
具体来说,你学到了:
- 大数定律支持这样的直觉:随着样本量的增加,样本将更好地代表总体。
- 如何在Python中开发一个小型示例来演示样本量增加如何减少误差。
- 大数定律对于理解机器学习中训练数据集、测试数据集的选择以及模型性能的评估至关重要。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







解释得很棒……谢谢Jason。今天我正好在看一个名为“学习可行吗”的视频,由 Abu – Mostafa 教授主讲,我认为在这里分享它会很有趣……他提到了 Hoeffding 不等式及其与机器学习背景下大数定律的关系…… IMO,Abu-Mustafa 教授在解释机器学习的数学方面时非常循循善诱。
https://www.youtube.com/watch?v=MEG35RDD7RA&index=1&list=PLD63A284B7615313A
感谢分享。
我无法使用第一个代码
请帮助
回溯(最近一次调用)
File “C:/Users/Acer E5-471G/PycharmProjects/test/Test.py”, line 4, in
from scipy.stats import norm
ModuleNotFoundError: No module named ‘scipy’
我得到了这个
看来你需要安装scipy,也许这个教程会有帮助
https://machinelearning.org.cn/setup-python-environment-machine-learning-deep-learning-anaconda/
我有一个问题。一个数字要多大才算大?根据概率,数字七应该出现次数最多。然而,在我这里,数字八出现的次数略高于七。是否有什么奇怪的事情在发生?
结果随样本数量缩放。
在您的情况下,即使样本量很大,您也可能遇到轻微的统计波动。您可以尝试增加到 100 万或 10 亿,您应该会看到与基本概率更强的收敛。
谢谢回复。我只是希望有一种方法可以知道在特定情况下需要多大的数字才能开始符合预期——或者有什么奇怪的事情在发生。我会继续掷骰子,看看会发生什么……是的,我实际上是在物理地掷骰子。
标准误差通常用于估计样本均值的误差,也许这对您有帮助?
嗨,Jason,
你能从你的帖子中回答这个吗?
“为大数定律适用的另外两个机器学习领域集思广益”。
还有另一篇帖子中的这个
“为应用机器学习中的另外两个领域提供中心极限定理可能相关的建议”
你好 Neha……你可能会发现以下内容很有趣
https://medium.com/analytics-vidhya/the-complete-beginners-guide-to-law-of-large-numbers-5-facts-about-law-of-large-numbers-e33cf0e10ffe
https://machinelearning.org.cn/a-gentle-introduction-to-the-central-limit-theorem-for-machine-learning/