向量空间模型简明介绍

向量空间模型用于考虑数据之间由向量表示的关系。它在信息检索系统中很受欢迎，但也可用于其他目的。通常，它允许我们从几何角度比较两个向量的相似性。

在本教程中，我们将了解什么是向量空间模型以及它的作用。

完成本教程后，您将了解：

• 什么是向量空间模型以及余弦相似度的性质
• 余弦相似度如何帮助您比较两个向量
• 余弦相似度和L2距离之间有什么区别

让我们开始吧。

向量空间模型简明介绍
照片作者：liamfletch，保留部分权利。

教程概述

本教程分为3个部分；它们是

1. 向量空间与余弦公式
2. 使用向量空间模型进行相似度计算
3. 向量空间模型和余弦距离的常见用法

向量空间与余弦公式

向量空间是一个定义某些向量运算的数学术语。通俗地说，我们可以将其想象成一个 $n$ 维度量空间，其中每个点都由一个 $n$ 维向量表示。在这个空间中，我们可以进行任何向量加法或标量-向量乘法。

考虑向量空间是有益的，因为它有助于将事物表示为向量。例如，在机器学习中，我们通常有一个具有多个特征的数据点。因此，将数据点表示为向量会很方便。

使用向量，我们可以计算其**范数**。最常见的是 L2 范数或向量的长度。对于同一向量空间中的两个向量，我们可以找到它们的差值。假设这是一个 3 维向量空间，两个向量为 $(x_1, x_2, x_3)$ 和 $(y_1, y_2, y_3)$。它们的差值是向量 $(y_1-x_1, y_2-x_2, y_3-x_3)$，差值的 L2 范数是这两个向量之间的**距离**，或者更准确地说，是欧几里得距离。

$$
\sqrt{(y_1-x_1)^2+(y_2-x_2)^2+(y_3-x_3)^2}
$$

除了距离，我们还可以考虑两个向量之间的**夹角**。如果我们考虑向量 $(x_1, x_2, x_3)$ 为 3D 坐标系中从点 $(0,0,0)$ 到 $(x_1,x_2,x_3)$ 的线段，那么还有另一条从 $(0,0,0)$ 到 $(y_1,y_2, y_3)$ 的线段。它们在相交处形成一个角度。

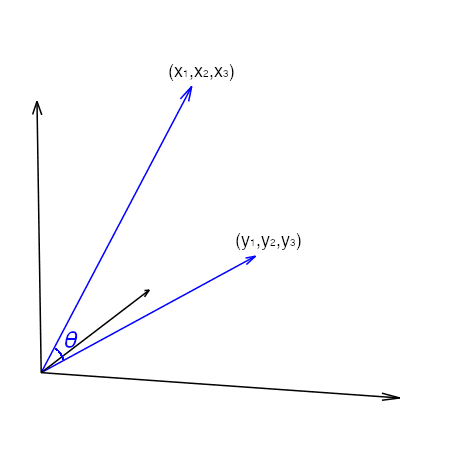
可以使用余弦公式找到两条线段之间的夹角。

$$
\cos \theta = \frac{a\cdot b} {\lVert a\rVert_2\lVert b\rVert_2}
$$

其中 $a\cdot b$ 是向量点积，$\lVert a\rVert_2$ 是向量 $a$ 的 L2 范数。该公式源于将点积视为向量 $a$ 在向量 $b$ 指向的方向上的投影。余弦的性质表明，随着角度 $\theta$ 从 0 度增加到 90 度，余弦值从 1 减小到 0。有时我们会将 $1-\cos\theta$ 称为**余弦距离**，因为它随着两个向量相互远离而从 0 变为 1。这是我们将在向量空间模型中利用的一个重要属性。

使用向量空间模型进行相似度计算

让我们看一个向量空间模型有用的例子。

世界银行收集了关于世界各国和地区的各种数据。虽然每个国家都不同，但我们可以尝试在向量空间模型下进行比较。为了方便起见，我们将使用 Python 中的 pandas_datareader 模块从世界银行读取数据。您可以使用 pip 或 conda 命令安装 pandas_datareader。

世界银行收集的数据系列通过标识符命名。例如，“SP.URB.TOTL”是国家/地区的总城市人口。许多系列是每年的。当我们下载一个系列时，我们必须输入开始和结束年份。通常数据更新不及时。因此，最好查看几年前的数据，而不是最近一年的数据，以避免数据丢失。

下面，我们尝试在 2010 年收集**所有**国家的某些经济数据。

上面我们获得了 2010 年各国的一些经济指标。wb.download() 函数将从世界银行下载数据并返回一个 pandas DataFrame。类似地，wb.get_countries() 将获取世界银行标识的国家和地区名称，我们将用它来过滤掉“东亚”和“世界”等非国家汇总。Pandas 允许通过布尔索引过滤行，其中 df["country"].isin(non_aggregates) 给出了一个布尔向量，指示哪些行在 non_aggregates 列表中，并在此基础上，df[df["country"].isin(non_aggregates)] 选择其中那些。出于各种原因，并非所有国家/地区都拥有所有数据。因此，我们使用 dropna() 删除那些数据缺失的。实际上，我们可能希望应用一些插补技术而不是仅仅删除它们。但作为一个例子，我们继续处理剩余的 174 个数据点。

为了更好地说明想法，而不是将实际操作隐藏在 pandas 或 numpy 函数中，我们首先将每个国家/地区的数据提取为向量。

我们创建的 Python 字典以每个国家的名称作为键，以经济指标作为 numpy 数组。有 5 个指标，因此每个指标都是一个 5 维向量。

这有什么帮助呢？我们可以使用每个国家的向量表示来查看它与另一个国家有多相似。让我们同时尝试差值的 L2 范数（欧几里得距离）和余弦距离。我们选择一个国家，例如澳大利亚，并根据选定的经济指标将其与列表中的所有其他国家进行比较。

在上面的 for 循环中，我们将 vecA 设置为目标国家（即澳大利亚）的向量，将 vecB 设置为另一个国家的向量。然后，我们计算它们差值的 L2 范数作为两个向量之间的欧几里得距离。我们还使用公式计算余弦相似度，并从中减去 1 以获得余弦距离。拥有一百多个国家，我们可以看到哪个国家与澳大利亚的欧几里得距离最近。

通过对结果进行排序，我们可以看到，在欧几里得距离方面，墨西哥最接近澳大利亚。然而，在余弦距离方面，哥伦比亚最接近澳大利亚。

为了理解为什么两种距离会产生不同的结果，我们可以观察这三个国家的指标如何相互比较。

从这张表中可以看出，澳大利亚和墨西哥的指标在数量级上非常接近。但是，如果比较同一国家内各项指标的比例，哥伦比亚与澳大利亚的匹配程度更高。实际上，从余弦公式可以看出：

$$
\cos \theta = \frac{a\cdot b} {\lVert a\rVert_2\lVert b\rVert_2} = \frac{a}{\lVert a\rVert_2} \cdot \frac{b} {\lVert b\rVert_2}
$$

这意味着两个向量之间的夹角的余弦是在它们被归一化为长度为 1 之后，对应向量的点积。因此，余弦距离实际上是在计算距离之前对数据应用了一个标量。

总而言之，以下是完整代码。

向量空间模型和余弦距离的常见用法

向量空间模型在信息检索系统中很常见。我们可以将文档（例如，一段话、一篇长文、一本书，甚至一个句子）表示为向量。这个向量可以很简单，例如计算文档中包含的单词数（即词袋模型），也可以是复杂的嵌入向量（例如 Doc2Vec）。然后，通过根据余弦距离对所有文档进行排序来回答查找最相关文档的查询。应该使用余弦距离，因为我们不想偏好较长或较短的文档，而是关注其内容。因此，我们利用其自带的归一化来考虑文档与查询的相关性，而不是查询中的词在文档中出现的次数。

如果我们考虑文档中的每个单词作为一个特征并计算余弦距离，这就是“硬”距离，因为我们不关心含义相似的单词（例如，“document”和“passage”含义相似，但“distance”不相似）。嵌入向量（如 word2vec）可以让我们考虑本体。在考虑了单词含义的情况下计算余弦距离是“**软余弦距离**”。像 gensim 这样的库提供了做到这一点的方法。

余弦距离和向量空间模型的另一个用例是计算机视觉。想象一下识别手势的任务，我们可以将手的某些部分（例如，五根手指）作为关键点。然后，将这些关键点的 (x,y) 坐标表示为向量，我们可以将其与现有数据库进行比较，看看哪个余弦距离最接近，从而确定它是什么手势。我们需要余弦距离，因为每个人的手大小都不同。我们不希望这影响我们对手势的判断。

正如您可能想象的那样，还有更多可以使用此技术的例子。

延伸阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 线性代数导论，第五版，2016。
• 信息检索导论, 2008.

软件

• 世界银行开放数据
• pandas 数据读取器
• Gensim

文章

• 维基百科上的向量空间模型

总结

在本教程中，您了解了用于测量向量相似性的向量空间模型。

具体来说，你学到了：

• 如何构建向量空间模型
• 如何在向量空间模型中计算余弦相似度以及由此产生的余弦距离
• 如何解释余弦距离与其他距离度量（如欧几里得距离）之间的差异
• 向量空间模型有哪些用途

掌握机器学习线性代数！

建立对线性代数的工作理解

...通过在 python 中编写代码

在我的新电子书中探索如何实现
机器学习线性代数

它提供关于以下主题的自学教程：
向量范数、矩阵乘法、张量、特征分解、SVD、PCA 等等...

最终理解数据的数学

跳过学术理论。只看结果。

查看内容