PyTorch 中的激活函数

作者： Muhammad Asad Iqbal Khan 发表于 2023 年 5 月 3 日在使用 PyTorch 进行深度学习 2

随着神经网络在机器学习领域越来越受欢迎，了解激活函数在其实现中所扮演的角色非常重要。在本文中，您将探索应用于神经网络中每个神经元输出的激活函数的概念，以引入模型的非线性。如果没有激活函数，神经网络将只是一系列线性变换，这将限制它们学习数据中复杂模式和关系的能力。

PyTorch 提供了各种激活函数，每种都有其独特的属性和用例。PyTorch 中一些常见的激活函数包括 ReLU、sigmoid 和 tanh。为特定问题选择正确的激活函数对于在神经网络中实现最佳性能可能是一个重要的考虑因素。您将看到如何在 PyTorch 中使用不同的激活函数训练神经网络并分析它们的性能。

在本教程中，您将学习

关于神经网络架构中使用的各种激活函数。
如何在 PyTorch 中实现激活函数。
激活函数在实际问题中如何相互比较。

让我们开始吧。

PyTorch 中的激活函数
图片由 Adrian Tam 使用稳定扩散生成。部分权利保留。

概述

本教程分为四个部分；它们是

逻辑激活函数
Tanh 激活函数
ReLU 激活函数
探索神经网络中的激活函数

逻辑激活函数

您将从逻辑函数开始，它是一种在神经网络中常用的激活函数，也称为 Sigmoid 函数。它接受任何输入并将其映射到 0 到 1 之间的一个值，这可以解释为概率。这使得它特别适用于二元分类任务，其中网络需要预测输入属于两个类别之一的概率。

逻辑函数的主要优点之一是它是可微分的，这意味着它可以在反向传播算法中用于训练神经网络。此外，它具有平滑的梯度，这有助于避免诸如梯度爆炸之类的问题。然而，它也可能在训练过程中引入梯度消失。

现在，让我们使用 PyTorch 在张量上应用逻辑函数并绘制它以查看其外观。

# importing the libraries
import torch
import matplotlib.pyplot as plt

# create a PyTorch tensor
x = torch.linspace(-10, 10, 100)

# apply the logistic activation function to the tensor
y = torch.sigmoid(x)

# plot the results with a custom color
plt.plot(x.numpy(), y.numpy(), color='purple')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Logistic Activation Function')
plt.show()

# 导入库

import torch

import matplotlib.pyplot as plt

# 创建一个 PyTorch 张量

x = torch.linspace(-10, 10, 100)

# 将逻辑激活函数应用于张量

y = torch.sigmoid(x)

# 使用自定义颜色绘制结果

plt.plot(x.numpy(), y.numpy(), color='purple')

plt.xlabel('输入')

plt.ylabel('输出')

plt.title('逻辑激活函数')

plt.show()

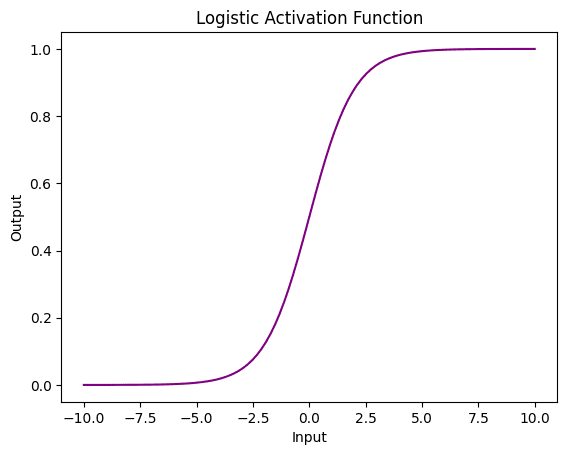
在上面的示例中，您使用了 Pytorch 库中的 torch.sigmoid() 函数将逻辑激活函数应用于张量 x。您使用了 matplotlib 库来创建带有自定义颜色的图。

Tanh 激活函数

接下来，您将研究 tanh 激活函数，它输出介于 -1 和 1 之间的值，平均输出为 0。这有助于确保神经网络层的输出保持在 0 附近，使其可用于归一化目的。Tanh 是一种平滑连续的激活函数，这使得在梯度下降过程中更容易优化。

与逻辑激活函数一样，tanh 函数也容易受到梯度消失问题的影响，特别是对于具有许多层的深度神经网络。这是因为对于大输入或小输入值，函数的斜率变得非常小，使得梯度难以通过网络传播。

此外，由于使用了指数函数，tanh 可能会计算成本高昂，特别是对于大型张量或在具有许多层的深度神经网络中使用时。

以下是如何将 tanh 应用于张量并可视化它。

# apply the tanh activation function to the tensor
y = torch.tanh(x)

# plot the results with a custom color
plt.plot(x.numpy(), y.numpy(), color='blue')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Tanh Activation Function')
plt.show()

# 将 tanh 激活函数应用于张量

y = torch.tanh(x)

# 使用自定义颜色绘制结果

plt.plot(x.numpy(), y.numpy(), color='blue')

plt.xlabel('输入')

plt.ylabel('输出')

plt.title('Tanh 激活函数')

plt.show()

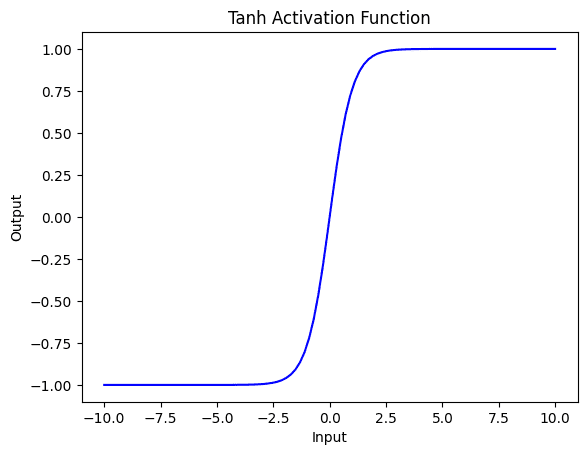
ReLU 激活函数

ReLU（Rectified Linear Unit）是神经网络中另一种常用的激活函数。与 sigmoid 和 tanh 函数不同，ReLU 是一种非饱和函数，这意味着它在输入范围的极端不会变平。相反，如果输入值为正，ReLU 只输出输入值；如果输入值为负，则输出 0。

这种简单的分段线性函数相对于 sigmoid 和 tanh 激活函数具有多项优点。首先，它的计算效率更高，使其非常适合大规模神经网络。其次，ReLU 已被证明不易受梯度消失问题的影响，因为它没有平坦的斜率。此外，ReLU 可以帮助稀疏化网络中神经元的激活，这可以带来更好的泛化能力。

以下是一个示例，说明如何将 ReLU 激活函数应用于 PyTorch 张量 x 并绘制结果。

# apply the ReLU activation function to the tensor
y = torch.relu(x)

# plot the results with a custom color
plt.plot(x.numpy(), y.numpy(), color='green')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('ReLU Activation Function')
plt.show()

# 将 ReLU 激活函数应用于张量

y = torch.relu(x)

# 使用自定义颜色绘制结果

plt.plot(x.numpy(), y.numpy(), color='green')

plt.xlabel('输入')

plt.ylabel('输出')

plt.title('ReLU 激活函数')

plt.show()

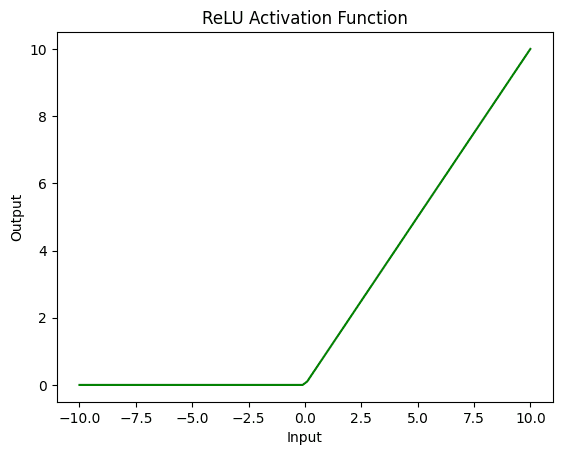
下面是打印上面讨论的所有激活函数的完整代码。

# importing the libraries
import torch
import matplotlib.pyplot as plt

# create a PyTorch tensor
x = torch.linspace(-10, 10, 100)

# apply the logistic activation function to the tensor and plot
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy(), color='purple')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Logistic Activation Function')
plt.show()

# apply the tanh activation function to the tensor and plot
y = torch.tanh(x)
plt.plot(x.numpy(), y.numpy(), color='blue')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Tanh Activation Function')
plt.show()

# apply the ReLU activation function to the tensor and plot
y = torch.relu(x)
plt.plot(x.numpy(), y.numpy(), color='green')
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('ReLU Activation Function')
plt.show()

# 导入库

import torch

import matplotlib.pyplot as plt

# 创建一个 PyTorch 张量

x = torch.linspace(-10, 10, 100)

# 将逻辑激活函数应用于张量并绘制

y = torch.sigmoid(x)

plt.plot(x.numpy(), y.numpy(), color='purple')

plt.xlabel('输入')

plt.ylabel('输出')

plt.title('逻辑激活函数')

plt.show()

# 将 tanh 激活函数应用于张量并绘制

y = torch.tanh(x)

plt.plot(x.numpy(), y.numpy(), color='blue')

plt.xlabel('输入')

plt.ylabel('输出')

plt.title('Tanh 激活函数')

plt.show()

# 将 ReLU 激活函数应用于张量并绘制

y = torch.relu(x)

plt.plot(x.numpy(), y.numpy(), color='green')

plt.xlabel('输入')

plt.ylabel('输出')

plt.title('ReLU 激活函数')

plt.show()

探索神经网络中的激活函数

激活函数在深度学习模型的训练中起着至关重要的作用，因为它们为网络引入了非线性，使其能够学习复杂的模式。

让我们以流行的 MNIST 数据集为例，它包含 70000 张 28×28 像素的手写数字灰度图像。您将创建一个简单的前馈神经网络来对这些数字进行分类，并尝试使用 ReLU、Sigmoid、Tanh 和 Leaky ReLU 等不同的激活函数。

import torchvision.datasets as datasets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader

# Load the MNIST dataset
transform = transforms.ToTensor()
train_dataset = datasets.MNIST(root='data/', train=True, transform=transform, download=True)
test_dataset = datasets.MNIST(root='data/', train=False, transform=transform, download=True)

train_loader = DataLoader(dataset=train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=64, shuffle=False)

import torchvision.datasets as datasets

import torchvision.transforms as transforms

from torch.utils.data import DataLoader

# 加载 MNIST 数据集

transform = transforms.ToTensor()

train_dataset = datasets.MNIST(root='data/', train=True, transform=transform, download=True)

test_dataset = datasets.MNIST(root='data/', train=False, transform=transform, download=True)

train_loader = DataLoader(dataset=train_dataset, batch_size=64, shuffle=True)

test_loader = DataLoader(dataset=test_dataset, batch_size=64, shuffle=False)

让我们创建一个继承自 nn.Module 的 NeuralNetwork 类。这个类有三个线性层和一个激活函数作为输入参数。forward 方法定义了网络的前向传播，除了最后一层之外，在每个线性层之后都应用激活函数。

import torch
import torch.nn as nn
import torch.optim as optim

class NeuralNetwork(nn.Module):
    def __init__(self, input_size, hidden_size, num_classes, activation_function):
        super(NeuralNetwork, self).__init__()
        self.layer1 = nn.Linear(input_size, hidden_size)
        self.layer2 = nn.Linear(hidden_size, hidden_size)
        self.layer3 = nn.Linear(hidden_size, num_classes)
        self.activation_function = activation_function

    def forward(self, x):
        x = self.activation_function(self.layer1(x))
        x = self.activation_function(self.layer2(x))
        x = self.layer3(x)
        return x

import torch

import torch.nn as nn

import torch.optim as optim

class NeuralNetwork(nn.Module):

def __init__(self, input_size, hidden_size, num_classes, activation_function):

super(NeuralNetwork, self).__init__()

self.layer1 = nn.Linear(input_size, hidden_size)

self.layer2 = nn.Linear(hidden_size, hidden_size)

self.layer3 = nn.Linear(hidden_size, num_classes)

self.activation_function = activation_function

def forward(self, x):

x = self.activation_function(self.layer1(x))

x = self.activation_function(self.layer2(x))

x = self.layer3(x)

return x

您已将 activation_function 参数添加到 NeuralNetwork 类中，这允许您插入任何您想要实验的激活函数。

使用不同的激活函数训练和测试模型

让我们创建函数来帮助训练。train() 函数训练网络一个 epoch。它遍历训练数据加载器，计算损失，并执行反向传播和优化。test() 函数在测试数据集上评估网络，计算测试损失和准确性。

def train(network, data_loader, criterion, optimizer, device):
    network.train()
    running_loss = 0.0

    for data, target in data_loader:
        data, target = data.to(device), target.to(device)
        data = data.view(data.shape[0], -1)

        optimizer.zero_grad()
        output = network(data)
        loss = criterion(output, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item() * data.size(0)

    return running_loss / len(data_loader.dataset)

def test(network, data_loader, criterion, device):
    network.eval()
    correct = 0
    total = 0
    test_loss = 0.0

    with torch.no_grad():
        for data, target in data_loader:
            data, target = data.to(device), target.to(device)
            data = data.view(data.shape[0], -1)

            output = network(data)
            loss = criterion(output, target)
            test_loss += loss.item() * data.size(0)
            _, predicted = torch.max(output.data, 1)
            total += target.size(0)
            correct += (predicted == target).sum().item()

    return test_loss / len(data_loader.dataset), 100 * correct / total

def train(network, data_loader, criterion, optimizer, device):

network.train()

running_loss = 0.0

for data, target in data_loader:

data, target = data.to(device), target.to(device)

data = data.view(data.shape[0], -1)

optimizer.zero_grad()

output = network(data)

loss = criterion(output, target)

loss.backward()

optimizer.step()

running_loss += loss.item() * data.size(0)

return running_loss / len(data_loader.dataset)

def test(network, data_loader, criterion, device):

network.eval()

correct = 0

total = 0

test_loss = 0.0

with torch.no_grad():

for data, target in data_loader:

data, target = data.to(device), target.to(device)

data = data.view(data.shape[0], -1)

output = network(data)

loss = criterion(output, target)

test_loss += loss.item() * data.size(0)

_, predicted = torch.max(output.data, 1)

total += target.size(0)

correct += (predicted == target).sum().item()

return test_loss / len(data_loader.dataset), 100 * correct / total

为了比较它们，我们创建一个激活函数字典并遍历它们。对于每个激活函数，您实例化 NeuralNetwork 类，定义准则（CrossEntropyLoss），并设置优化器（Adam）。然后，训练模型指定数量的 epoch，在每个 epoch 中调用 train() 和 test() 函数来评估模型的性能。您将每个 epoch 的训练损失、测试损失和测试准确性存储在结果字典中。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
input_size = 784
hidden_size = 128
num_classes = 10
num_epochs = 10
learning_rate = 0.001

activation_functions = {
    'ReLU': nn.ReLU(),
    'Sigmoid': nn.Sigmoid(),
    'Tanh': nn.Tanh(),
    'LeakyReLU': nn.LeakyReLU()
}

results = {}

# Train and test the model with different activation functions
for name, activation_function in activation_functions.items():
    print(f"Training with {name} activation function...")

    model = NeuralNetwork(input_size, hidden_size, num_classes, activation_function).to(device)
    criterion = nn.CrossEntropyLoss()
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)

    train_loss_history = []
    test_loss_history = []
    test_accuracy_history = []

    for epoch in range(num_epochs):
        train_loss = train(model, train_loader, criterion, optimizer, device)
        test_loss, test_accuracy = test(model, test_loader, criterion, device)

        train_loss_history.append(train_loss)
        test_loss_history.append(test_loss)
        test_accuracy_history.append(test_accuracy)

        print(f"Epoch [{epoch+1}/{num_epochs}], Test Loss: {test_loss:.4f}, Test Accuracy: {test_accuracy:.2f}%")

    results[name] = {
        'train_loss_history': train_loss_history,
        'test_loss_history': test_loss_history,
        'test_accuracy_history': test_accuracy_history
    }

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

input_size = 784

hidden_size = 128

num_classes = 10

num_epochs = 10

learning_rate = 0.001

activation_functions = {

'ReLU': nn.ReLU(),

'Sigmoid': nn.Sigmoid(),

'Tanh': nn.Tanh(),

'LeakyReLU': nn.LeakyReLU()

}

results = {}

# 使用不同的激活函数训练和测试模型

for name, activation_function in activation_functions.items():

print(f"正在使用 {name} 激活函数进行训练...")

model = NeuralNetwork(input_size, hidden_size, num_classes, activation_function).to(device)

criterion = nn.CrossEntropyLoss()

optimizer = optim.Adam(model.parameters(), lr=learning_rate)

train_loss_history = []

test_loss_history = []

test_accuracy_history = []

for epoch in range(num_epochs):

train_loss = train(model, train_loader, criterion, optimizer, device)

test_loss, test_accuracy = test(model, test_loader, criterion, device)

train_loss_history.append(train_loss)

test_loss_history = test_loss_history.append(test_loss)

test_accuracy_history = test_accuracy_history.append(test_accuracy)

print(f"Epoch [{epoch+1}/{num_epochs}], 测试损失: {test_loss:.4f}, 测试准确率: {test_accuracy:.2f}%")

results[name] = {

'train_loss_history': train_loss_history,

'test_loss_history': test_loss_history,

'test_accuracy_history': test_accuracy_history

}

当您运行上述代码时，它会打印

Training with ReLU activation function...
Epoch [1/10], Test Loss: 0.1589, Test Accuracy: 95.02%
Epoch [2/10], Test Loss: 0.1138, Test Accuracy: 96.52%
Epoch [3/10], Test Loss: 0.0886, Test Accuracy: 97.15%
Epoch [4/10], Test Loss: 0.0818, Test Accuracy: 97.50%
Epoch [5/10], Test Loss: 0.0783, Test Accuracy: 97.47%
Epoch [6/10], Test Loss: 0.0754, Test Accuracy: 97.80%
Epoch [7/10], Test Loss: 0.0832, Test Accuracy: 97.56%
Epoch [8/10], Test Loss: 0.0783, Test Accuracy: 97.78%
Epoch [9/10], Test Loss: 0.0789, Test Accuracy: 97.75%
Epoch [10/10], Test Loss: 0.0735, Test Accuracy: 97.99%
Training with Sigmoid activation function...
Epoch [1/10], Test Loss: 0.2420, Test Accuracy: 92.81%
Epoch [2/10], Test Loss: 0.1718, Test Accuracy: 94.99%
Epoch [3/10], Test Loss: 0.1339, Test Accuracy: 96.06%
Epoch [4/10], Test Loss: 0.1141, Test Accuracy: 96.42%
Epoch [5/10], Test Loss: 0.1004, Test Accuracy: 97.00%
Epoch [6/10], Test Loss: 0.0909, Test Accuracy: 97.10%
Epoch [7/10], Test Loss: 0.0846, Test Accuracy: 97.28%
Epoch [8/10], Test Loss: 0.0797, Test Accuracy: 97.42%
Epoch [9/10], Test Loss: 0.0785, Test Accuracy: 97.58%
Epoch [10/10], Test Loss: 0.0795, Test Accuracy: 97.58%
Training with Tanh activation function...
Epoch [1/10], Test Loss: 0.1660, Test Accuracy: 95.17%
Epoch [2/10], Test Loss: 0.1152, Test Accuracy: 96.47%
Epoch [3/10], Test Loss: 0.1057, Test Accuracy: 96.86%
Epoch [4/10], Test Loss: 0.0865, Test Accuracy: 97.21%
Epoch [5/10], Test Loss: 0.0760, Test Accuracy: 97.61%
Epoch [6/10], Test Loss: 0.0856, Test Accuracy: 97.23%
Epoch [7/10], Test Loss: 0.0735, Test Accuracy: 97.66%
Epoch [8/10], Test Loss: 0.0790, Test Accuracy: 97.67%
Epoch [9/10], Test Loss: 0.0805, Test Accuracy: 97.47%
Epoch [10/10], Test Loss: 0.0834, Test Accuracy: 97.82%
Training with LeakyReLU activation function...
Epoch [1/10], Test Loss: 0.1587, Test Accuracy: 95.14%
Epoch [2/10], Test Loss: 0.1084, Test Accuracy: 96.37%
Epoch [3/10], Test Loss: 0.0861, Test Accuracy: 97.22%
Epoch [4/10], Test Loss: 0.0883, Test Accuracy: 97.06%
Epoch [5/10], Test Loss: 0.0870, Test Accuracy: 97.37%
Epoch [6/10], Test Loss: 0.0929, Test Accuracy: 97.26%
Epoch [7/10], Test Loss: 0.0824, Test Accuracy: 97.54%
Epoch [8/10], Test Loss: 0.0785, Test Accuracy: 97.77%
Epoch [9/10], Test Loss: 0.0908, Test Accuracy: 97.92%
Epoch [10/10], Test Loss: 0.1012, Test Accuracy: 97.76%

正在使用 ReLU 激活函数进行训练...

Epoch [1/10], 测试损失: 0.1589, 测试准确率: 95.02%

Epoch [2/10], 测试损失: 0.1138, 测试准确率: 96.52%

Epoch [3/10], 测试损失: 0.0886, 测试准确率: 97.15%

Epoch [4/10], 测试损失: 0.0818, 测试准确率: 97.50%

Epoch [5/10], 测试损失: 0.0783, 测试准确率: 97.47%

Epoch [6/10], 测试损失: 0.0754, 测试准确率: 97.80%

Epoch [7/10], 测试损失: 0.0832, 测试准确率: 97.56%

Epoch [8/10], 测试损失: 0.0783, 测试准确率: 97.78%

Epoch [9/10], 测试损失: 0.0789, 测试准确率: 97.75%

Epoch [10/10], 测试损失: 0.0735, 测试准确率: 97.99%

正在使用 Sigmoid 激活函数进行训练...

Epoch [1/10], 测试损失: 0.2420, 测试准确率: 92.81%

Epoch [2/10], 测试损失: 0.1718, 测试准确率: 94.99%

Epoch [3/10], 测试损失: 0.1339, 测试准确率: 96.06%

Epoch [4/10], 测试损失: 0.1141, 测试准确率: 96.42%

Epoch [5/10], 测试损失: 0.1004, 测试准确率: 97.00%

Epoch [6/10], 测试损失: 0.0909, 测试准确率: 97.10%

Epoch [7/10], 测试损失: 0.0846, 测试准确率: 97.28%

Epoch [8/10], 测试损失: 0.0797, 测试准确率: 97.42%

Epoch [9/10], 测试损失: 0.0785, 测试准确率: 97.58%

Epoch [10/10], 测试损失: 0.0795, 测试准确率: 97.58%

正在使用 Tanh 激活函数进行训练...

Epoch [1/10], 测试损失: 0.1660, 测试准确率: 95.17%

Epoch [2/10], 测试损失: 0.1152, 测试准确率: 96.47%

Epoch [3/10], 测试损失: 0.1057, 测试准确率: 96.86%

Epoch [4/10], 测试损失: 0.0865, 测试准确率: 97.21%

Epoch [5/10], 测试损失: 0.0760, 测试准确率: 97.61%

Epoch [6/10], 测试损失: 0.0856, 测试准确率: 97.23%

Epoch [7/10], 测试损失: 0.0735, 测试准确率: 97.66%

Epoch [8/10], 测试损失: 0.0790, 测试准确率: 97.67%

Epoch [9/10], 测试损失: 0.0805, 测试准确率: 97.47%

Epoch [10/10], 测试损失: 0.0834, 测试准确率: 97.82%

正在使用 LeakyReLU 激活函数进行训练...

Epoch [1/10], 测试损失: 0.1587, 测试准确率: 95.14%

Epoch [2/10], 测试损失: 0.1084, 测试准确率: 96.37%

Epoch [3/10], 测试损失: 0.0861, 测试准确率: 97.22%

Epoch [4/10], 测试损失: 0.0883, 测试准确率: 97.06%

Epoch [5/10], 测试损失: 0.0870, 测试准确率: 97.37%

Epoch [6/10], 测试损失: 0.0929, 测试准确率: 97.26%

Epoch [7/10], 测试损失: 0.0824, 测试准确率: 97.54%

Epoch [8/10], 测试损失: 0.0785, 测试准确率: 97.77%

Epoch [9/10], 测试损失: 0.0908, 测试准确率: 97.92%

Epoch [10/10], 测试损失: 0.1012, 测试准确率: 97.76%

您可以使用 Matplotlib 创建图表，比较每个激活函数的性能。您可以创建三个独立的图表，以可视化每个激活函数在不同 epoch 中的训练损失、测试损失和测试准确性。

import matplotlib.pyplot as plt

# Plot the training loss
plt.figure()
for name, data in results.items():
    plt.plot(data['train_loss_history'], label=name)
plt.xlabel('Epoch')
plt.ylabel('Training Loss')
plt.legend()
plt.show()

# Plot the testing loss
plt.figure()
for name, data in results.items():
    plt.plot(data['test_loss_history'], label=name)
plt.xlabel('Epoch')
plt.ylabel('Testing Loss')
plt.legend()
plt.show()

# Plot the testing accuracy
plt.figure()
for name, data in results.items():
    plt.plot(data['test_accuracy_history'], label=name)
plt.xlabel('Epoch')
plt.ylabel('Testing Accuracy')
plt.legend()
plt.show()

import matplotlib.pyplot as plt

# 绘制训练损失

plt.figure()

for name, data in results.items():

plt.plot(data['train_loss_history'], label=name)

plt.xlabel('Epoch')

plt.ylabel('训练损失')

plt.legend()

plt.show()

# 绘制测试损失

plt.figure()

for name, data in results.items():

plt.plot(data['test_loss_history'], label=name)

plt.xlabel('Epoch')

plt.ylabel('测试损失')

plt.legend()

plt.show()

# 绘制测试准确率

plt.figure()

for name, data in results.items():

plt.plot(data['test_accuracy_history'], label=name)

plt.xlabel('Epoch')

plt.ylabel('测试准确率')

plt.legend()

plt.show()

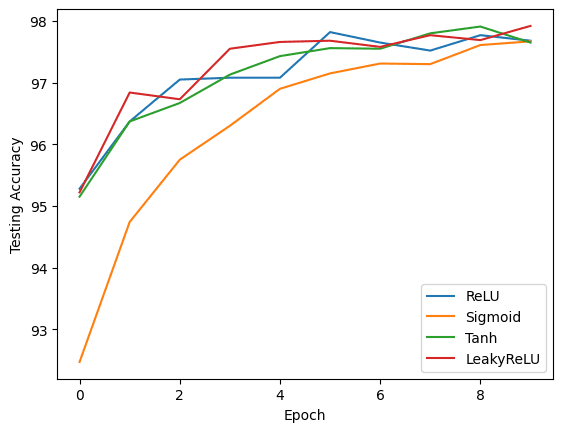
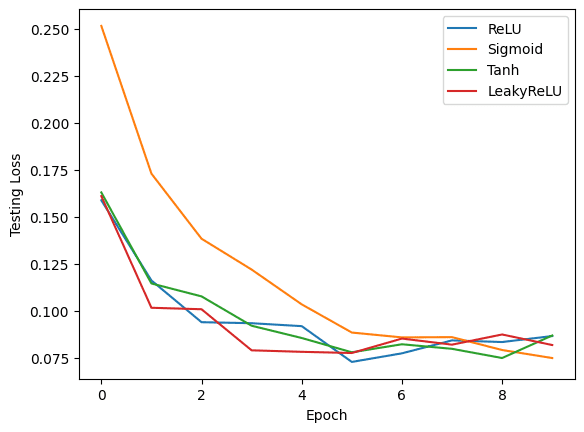
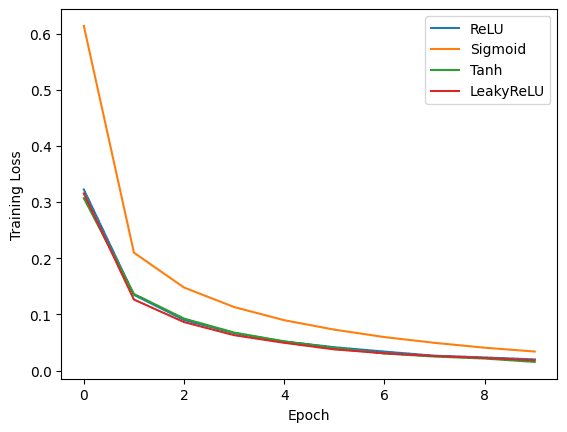
这些图表提供了每个激活函数性能的视觉比较。通过分析结果，您可以确定哪种激活函数最适合本示例中使用的特定任务和数据集。

总结

在本教程中，您已经实现了 PyTorch 中一些最流行的激活函数。您还了解了如何使用流行的 MNIST 数据集，在 PyTorch 中使用不同的激活函数训练神经网络。您探索了 ReLU、Sigmoid、Tanh 和 Leaky ReLU 激活函数，并通过绘制训练损失、测试损失和测试准确率来分析它们的性能。
如您所见，激活函数的选择在模型性能中起着至关重要的作用。但是，请记住，最佳激活函数可能会因任务和数据集而异。