梯度下降是一种优化算法,它沿着目标函数的负梯度方向移动,以找到函数的最小值。
梯度下降的一个局限是,它对所有输入变量都使用单一的步长(学习率)。诸如 AdaGrad 和 RMSProp 等梯度下降的扩展算法更新了算法,使其为每个输入变量使用单独的步长,但这可能导致步长迅速减小到非常小的值。
自适应移动估计算法,简称Adam,是梯度下降的扩展,也是 AdaGrad 和 RMSProp 等技术的自然继承者,它能自动调整目标函数每个输入变量的学习率,并通过使用梯度指数衰减的移动平均值来更新变量,从而进一步平滑搜索过程。
在本教程中,您将学习如何从头开始开发具有 Adam 优化算法的梯度下降。
完成本教程后,您将了解:
- 梯度下降是一种优化算法,它利用目标函数的梯度来导航搜索空间。
- 梯度下降可以通过一种衰减的偏导数平均值,称为 Adam,来更新,以使用每个输入变量的自动自适应步长。
- 如何从头开始实现 Adam 优化算法,并将其应用于目标函数并评估结果。
立即开始您的项目,阅读我的新书《机器学习优化》,其中包括分步教程和所有示例的Python源代码文件。
让我们开始吧。
从零开始的 Adam 梯度下降优化
照片来源:Don Graham,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 梯度下降
- Adam 优化算法
- Adam 梯度下降
- 二维测试问题
- Adam 梯度下降优化
- Adam 可视化
梯度下降
梯度下降是一种优化算法。
它在技术上被称为一阶优化算法,因为它明确使用了目标函数的一阶导数。
- 一阶方法依赖梯度信息来帮助指导寻找最小值……
——第69页,《优化算法》,2019年。
一阶导数,或简单地称为“导数”,是目标函数在特定点(例如,对于特定输入)的改变量率或斜率。
如果目标函数有多个输入变量,则称为多元函数,输入变量可以看作是一个向量。反过来,多元目标函数的导数也可以看作是一个向量,通常称为梯度。
- 梯度:多元目标函数的一阶导数。
导数或梯度指向特定输入处目标函数最陡峭上升的方向。
梯度下降指一种最小化优化算法,它沿着目标函数的负梯度方向“下坡”移动,以找到函数的最小值。
梯度下降算法需要一个正在优化的目标函数和目标函数的导数函数。目标函数f()返回给定输入集的分数,而导数函数f'()给出给定输入集的目标函数导数。
梯度下降算法需要问题中的一个起点(x),例如输入空间中随机选择的一个点。
然后计算导数,并在输入空间中迈出一步,预计会导致目标函数下坡移动(假设我们正在最小化目标函数)。
通过首先计算在输入空间中移动的距离(计算方法为步长(称为 alpha 或学习率)乘以梯度)来实现下行移动。然后将其从当前点减去,确保我们沿着梯度的反方向移动,即沿着目标函数的下坡方向移动。
- x(t) = x(t-1) – step_size * f'(x(t-1))
目标函数在给定点的斜率越大,梯度的幅度就越大,进而搜索空间中步长就越大。步长的大小通过步长超参数进行缩放。
- **步长**(*alpha*):控制算法每次迭代中在搜索空间中逆着梯度移动距离的超参数。
如果步长太小,在搜索空间中的移动会很小,搜索将花费很长时间。如果步长太大,搜索可能会在搜索空间中跳跃并跳过最优解。
现在我们熟悉了梯度下降优化算法,让我们来看看 Adam 算法。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
Adam 优化算法
自适应移动估计算法,简称 Adam,是梯度下降优化算法的扩展。
该算法由 Diederik Kingma 和 Jimmy Lei Ba 在 2014 年的论文“Adam: A Method for Stochastic Optimization”中进行了描述。
Adam 旨在加速优化过程,例如减少达到最优值所需的函数评估次数,或提高优化算法的能力,例如获得更好的最终结果。
这是通过为正在优化的每个输入参数计算步长来实现的。重要的是,每个步长在整个搜索过程中都会根据遇到的每个变量的梯度(偏导数)进行自动调整。
我们提出 Adam,一种高效的随机优化方法,该方法仅需要一阶梯度且内存需求很小。该方法根据梯度的第一和第二矩估计来计算不同参数的个体自适应学习率;Adam 这个名字来源于自适应矩估计。
— Adam: A Method for Stochastic Optimization
这包括为搜索的每个参数维护一个梯度的一阶和二阶矩,例如指数衰减的平均梯度(一阶矩)和方差(二阶矩)。
移动平均值本身是梯度的一阶矩(均值)和二阶原始矩(非中心方差)的估计。
— Adam: A Method for Stochastic Optimization
让我们逐步了解算法的每个元素。
首先,我们必须维护一个矩向量和指数加权无穷范数,分别对应于搜索中每个待优化参数,称为 m 和 v(实际上是希腊字母 nu)。它们在搜索开始时初始化为 0.0。
- m = 0
- v = 0
算法以迭代方式执行,时间 t 从 t=1 开始,每次迭代都涉及计算一组新的参数值 x,例如从 x(t-1) 到 x(t)。
如果我们将重点放在更新一个参数上,可能会更容易理解该算法,这可以通过向量运算推广到更新所有参数。
首先,计算当前时间步的梯度(偏导数)。
- g(t) = f'(x(t-1))
接下来,使用梯度和超参数beta1更新一阶矩。
- m(t) = beta1 * m(t-1) + (1 – beta1) * g(t)
然后使用平方梯度和超参数beta2更新二阶矩。
- v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2
一阶和二阶矩由于用零值初始化而存在偏差。
……这些移动平均值初始化为零(向量),导致矩估计倾向于零,尤其是在初始时间步,特别是当衰减率很小时(即 beta 接近 1)。好消息是,这种初始化偏差可以轻松地得到补偿,从而得到偏差校正的估计……
— Adam: A Method for Stochastic Optimization
接下来,一阶和二阶矩将进行偏差校正,从一阶矩开始。
- mhat(t) = m(t) / (1 – beta1(t))
然后是二阶矩。
- vhat(t) = v(t) / (1 – beta2(t))
注意,beta1(t)和beta2(t)指的是在算法迭代过程中按计划衰减的 beta1 和 beta2 超参数。可以使用静态衰减计划,尽管论文推荐以下方法。
- beta1(t) = beta1^t
- beta2(t) = beta2^t
最后,我们可以计算此迭代的参数值。
- x(t) = x(t-1) – alpha * mhat(t) / (sqrt(vhat(t)) + eps)
其中alpha是步长超参数,eps是一个小值(epsilon),例如 1e-8,它确保我们不会遇到除零错误,而sqrt()是平方根函数。
注意,可以使用论文中列出的更新规则的一个更有效的重排序。
- alpha(t) = alpha * sqrt(1 – beta2(t)) / (1 – beta1(t))
- x(t) = x(t-1) – alpha(t) * m(t) / (sqrt(v(t)) + eps)
回顾一下,该算法有三个超参数,它们是:
- alpha:初始步长(学习率),典型值为 0.001。
- **beta1**:一阶动量的衰减因子,典型值为 0.9。
- **beta2**:无穷范数的衰减因子,典型值为 0.999。
就是这样。
有关 Adam 算法在 Adam 算法背景下的完整推导,我建议阅读该论文。
接下来,我们看看如何在Python中从头开始实现该算法。
Adam 梯度下降
在本节中,我们将探讨如何实现带有 Adam 的梯度下降优化算法。
二维测试问题
首先,让我们定义一个优化函数。
我们将使用一个简单的二维函数,它将每个维度的输入平方,并将有效输入范围定义为-1.0到1.0。
下面的 objective() 函数实现了这个功能。
|
1 2 3 |
# 目标函数 def objective(x, y): return x**2.0 + y**2.0 |
我们可以创建一个数据集的三维图来感受响应曲面的曲率。
下面列出了绘制目标函数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 绘制测试函数的三维图 from numpy import arange from numpy import meshgrid from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -1.0, 1.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建目标函数的三维曲面图。
我们可以看到熟悉的碗形,全局最小值在 f(0, 0) = 0。
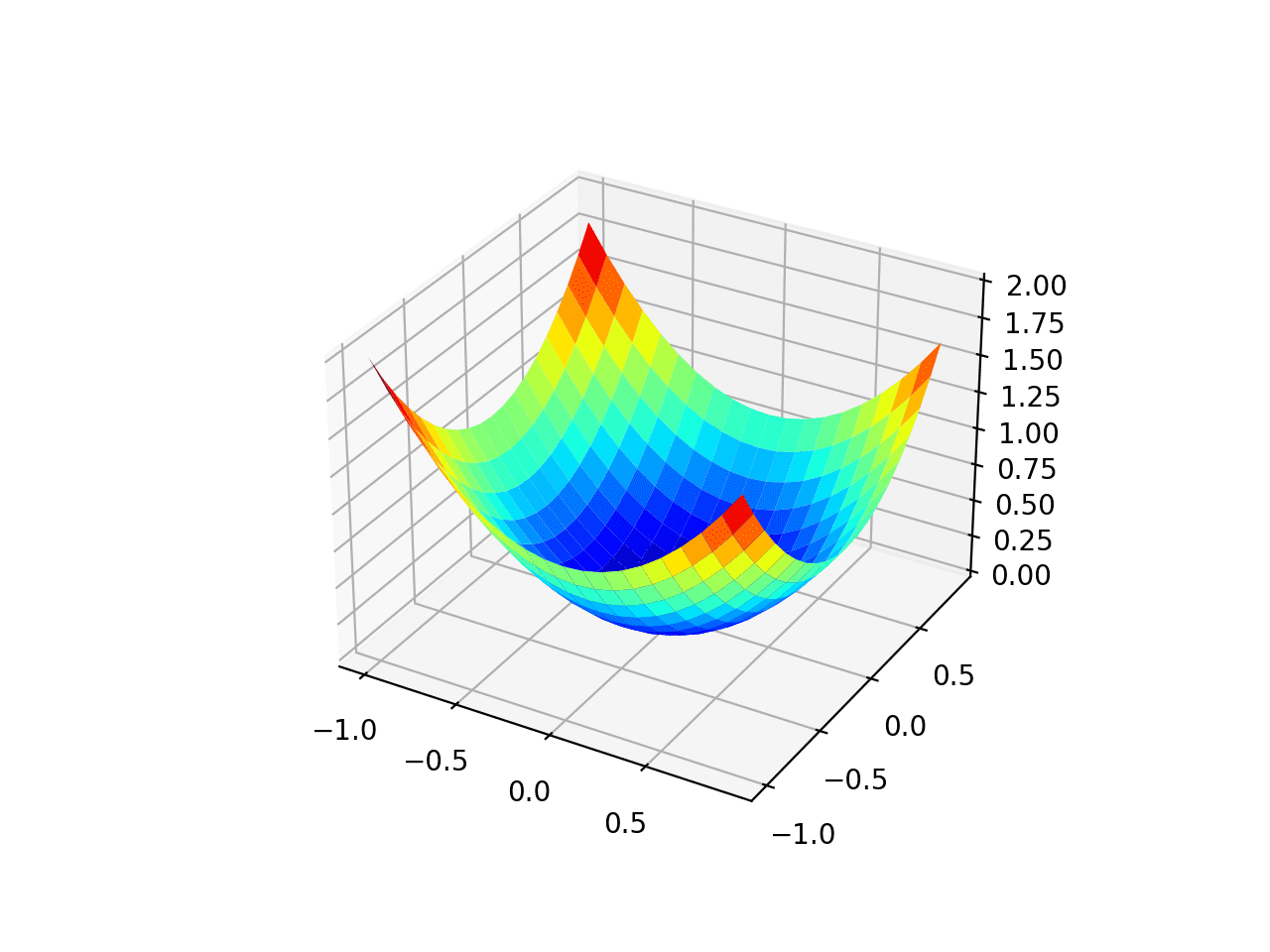
测试目标函数的三维图
我们还可以创建函数的二维图。这将在以后我们想要绘制搜索进度时提供帮助。
以下示例创建了目标函数的等高线图。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 绘制测试函数的等高线图 from numpy import asarray from numpy import arange from numpy import meshgrid from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 以 0.1 为增量均匀采样输入范围 xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建目标函数的二维等高线图。
我们可以看到碗状被压缩成用颜色梯度显示的等高线。我们将使用这个图来绘制搜索过程中探索的特定点。
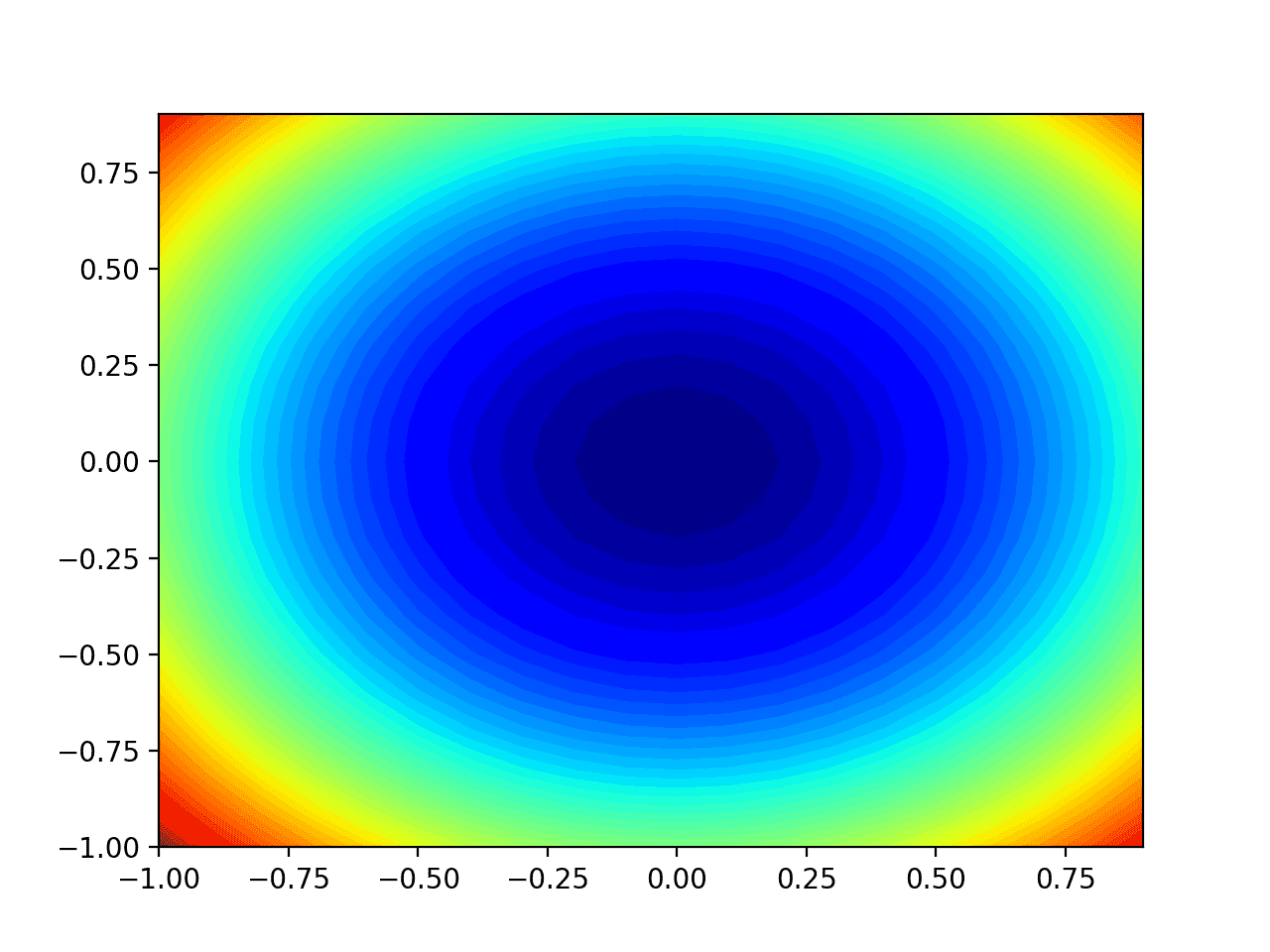
测试目标函数的二维等高线图
现在我们有了测试目标函数,让我们看看如何实现 Adam 优化算法。
Adam 梯度下降优化
我们可以将带有 Adam 的梯度下降应用于测试问题。
首先,我们需要一个函数来计算此函数的导数。
- f(x) = x^2
- f'(x) = x * 2
x^2 的导数在每个维度上都是 x * 2。derivative() 函数在下面实现了这一点。
|
1 2 3 |
# 目标函数的导数 def derivative(x, y): return asarray([x * 2.0, y * 2.0]) |
接下来,我们可以实现梯度下降优化。
首先,我们可以在问题的边界内选择一个随机点作为搜索的起点。
这假设我们有一个数组,它定义了搜索的边界,每行一个维度,第一列定义最小值,第二列定义最大值。
|
1 2 3 4 |
... # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) score = objective(x[0], x[1]) |
接下来,我们需要初始化一阶和二阶矩为零。
|
1 2 3 4 |
... # 初始化一阶和二阶矩 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] |
然后我们运行由“_n_iter_”超参数定义的固定迭代次数。
|
1 2 3 4 |
... # 运行梯度下降迭代 for t in range(n_iter): ... |
第一步是使用 *derivative()* 函数计算当前解的梯度。
|
1 2 3 |
... # 计算梯度 gradient = derivative(solution[0], solution[1]) |
第一步是计算当前参数集的导数。
|
1 2 3 |
... # 计算梯度 g(t) g = derivative(x[0], x[1]) |
接下来,我们需要执行 Adam 更新计算。我们将使用命令式编程风格逐个变量进行这些计算,以提高可读性。
实际上,我建议使用NumPy向量操作以提高效率。
|
1 2 3 4 |
... # 逐个变量构建解 for i in range(x.shape[0]): ... |
首先,我们需要计算矩。
|
1 2 3 |
... # m(t) = beta1 * m(t-1) + (1 - beta1) * g(t) m[i] = beta1 * m[i] + (1.0 - beta1) * g[i] |
然后是二阶矩。
|
1 2 3 |
... # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 - beta2) * g[i]**2 |
然后是第一和第二矩的偏差校正。
|
1 2 3 4 5 |
... # mhat(t) = m(t) / (1 - beta1(t)) mhat = m[i] / (1.0 - beta1**(t+1)) # vhat(t) = v(t) / (1 - beta2(t)) vhat = v[i] / (1.0 - beta2**(t+1)) |
然后是更新后的变量值。
|
1 2 3 |
... # x(t) = x(t-1) - alpha * mhat(t) / (sqrt(vhat(t)) + eps) x[i] = x[i] - alpha * mhat / (sqrt(vhat) + eps) |
然后对每个要优化的参数重复此操作。
在迭代结束时,我们可以评估新的参数值并报告搜索的性能。
|
1 2 3 4 5 |
... # 评估候选点 score = objective(x[0], x[1]) # 报告进展 print('>%d f(%s) = %.5f' % (t, x, score)) |
我们可以将所有这些内容整合到一个名为adam()的函数中,该函数接受目标函数和导数函数的名称以及算法超参数,并返回搜索结束时找到的最佳解决方案及其评估值。
完整的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
# 带有 adam 的梯度下降算法 def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e-8): # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) score = objective(x[0], x[1]) # 初始化一阶和二阶矩 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降更新 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量构建解 for i in range(x.shape[0]): # m(t) = beta1 * m(t-1) + (1 - beta1) * g(t) m[i] = beta1 * m[i] + (1.0 - beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 - beta2) * g[i]**2 # mhat(t) = m(t) / (1 - beta1(t)) mhat = m[i] / (1.0 - beta1**(t+1)) # vhat(t) = v(t) / (1 - beta2(t)) vhat = v[i] / (1.0 - beta2**(t+1)) # x(t) = x(t-1) - alpha * mhat(t) / (sqrt(vhat(t)) + eps) x[i] = x[i] - alpha * mhat / (sqrt(vhat) + eps) # 评估候选点 score = objective(x[0], x[1]) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return [x, score] |
注意:为了提高可读性,我们故意使用了列表和命令式编码风格,而不是向量化操作。您可以随时将实现调整为使用 NumPy 数组的向量化实现,以获得更好的性能。
然后我们可以定义我们的超参数并调用adam()函数来优化我们的测试目标函数。
在这种情况下,我们将使用该算法的 60 次迭代,初始步长为 0.02,beta1 和 beta2 的值为 0.8 和 0.999。这些超参数值是经过一些试错找到的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
... # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 60 # 步长 alpha = 0.02 # 平均梯度因子 beta1 = 0.8 # 平均梯度平方因子 beta2 = 0.999 # 使用 Adam 执行梯度下降搜索 best, score = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) print('Done!') print('f(%s) = %f' % (best, score)) |
将所有这些结合起来,下面列出了使用 Adam 进行梯度下降优化的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
# 使用 Adam 对二维测试函数进行梯度下降优化 from math import sqrt from numpy import asarray from numpy.random import rand from numpy.random import seed # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 目标函数的导数 def derivative(x, y): return asarray([x * 2.0, y * 2.0]) # 带有 adam 的梯度下降算法 def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e-8): # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) score = objective(x[0], x[1]) # 初始化一阶和二阶矩 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降更新 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量构建解 for i in range(x.shape[0]): # m(t) = beta1 * m(t-1) + (1 - beta1) * g(t) m[i] = beta1 * m[i] + (1.0 - beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 - beta2) * g[i]**2 # mhat(t) = m(t) / (1 - beta1(t)) mhat = m[i] / (1.0 - beta1**(t+1)) # vhat(t) = v(t) / (1 - beta2(t)) vhat = v[i] / (1.0 - beta2**(t+1)) # x(t) = x(t-1) - alpha * mhat(t) / (sqrt(vhat(t)) + eps) x[i] = x[i] - alpha * mhat / (sqrt(vhat) + eps) # 评估候选点 score = objective(x[0], x[1]) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return [x, score] # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 60 # 步长 alpha = 0.02 # 平均梯度因子 beta1 = 0.8 # 平均梯度平方因子 beta2 = 0.999 # 使用 Adam 执行梯度下降搜索 best, score = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) print('Done!') print('f(%s) = %f' % (best, score)) |
运行示例将 Adam 优化算法应用于我们的测试问题,并报告算法每次迭代的搜索性能。
注意:由于算法或评估程序的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑运行几次示例并比较平均结果。
在这种情况下,我们可以看到经过大约 53 次搜索迭代后,找到了一个接近最优的解,输入值接近 0.0 和 0.0,评分为 0.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... >50 f([-0.00056912 -0.00321961]) = 0.00001 >51 f([-0.00052452 -0.00286514]) = 0.00001 >52 f([-0.00043908 -0.00251304]) = 0.00001 >53 f([-0.0003283 -0.00217044]) = 0.00000 >54 f([-0.00020731 -0.00184302]) = 0.00000 >55 f([-8.95352320e-05 -1.53514076e-03]) = 0.00000 >56 f([ 1.43050285e-05 -1.25002847e-03]) = 0.00000 >57 f([ 9.67123406e-05 -9.89850279e-04]) = 0.00000 >58 f([ 0.00015359 -0.00075587]) = 0.00000 >59 f([ 0.00018407 -0.00054858]) = 0.00000 完成! f([ 0.00018407 -0.00054858]) = 0.000000 |
Adam 可视化
我们可以在域的等高线图上绘制 Adam 搜索的进度。
这可以提供对算法迭代过程中搜索进展的直观感受。
我们必须更新 `adam()` 函数,以维护一个搜索过程中找到的所有解的列表,然后在搜索结束时返回该列表。
包含这些更改的更新版本函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 带有 adam 的梯度下降算法 def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e-8): solutions = list() # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) score = objective(x[0], x[1]) # 初始化一阶和二阶矩 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降更新 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量构建解 for i in range(bounds.shape[0]): # m(t) = beta1 * m(t-1) + (1 - beta1) * g(t) m[i] = beta1 * m[i] + (1.0 - beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 - beta2) * g[i]**2 # mhat(t) = m(t) / (1 - beta1(t)) mhat = m[i] / (1.0 - beta1**(t+1)) # vhat(t) = v(t) / (1 - beta2(t)) vhat = v[i] / (1.0 - beta2**(t+1)) # x(t) = x(t-1) - alpha * mhat(t) / (sqrt(vhat(t)) + ep) x[i] = x[i] - alpha * mhat / (sqrt(vhat) + eps) # 评估候选点 score = objective(x[0], x[1]) # 跟踪解决方案 solutions.append(x.copy()) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return solutions |
然后我们可以像以前一样执行搜索,这次检索解决方案列表而不是最终的最佳解决方案。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 60 # 步长 alpha = 0.02 # 平均梯度因子 beta1 = 0.8 # 平均梯度平方因子 beta2 = 0.999 # 使用 Adam 执行梯度下降搜索 solutions = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) |
然后我们可以像以前一样创建目标函数的等高线图。
|
1 2 3 4 5 6 7 8 9 10 |
... # 以 0.1 为增量均匀采样输入范围 xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') |
最后,我们可以将搜索过程中找到的每个解决方案绘制成一个由线连接的白点。
|
1 2 3 4 |
... # 将样本绘制为黑色圆圈 solutions = asarray(solutions) pyplot.plot(solutions[:, 0], solutions[:, 1], '.-', color='w') |
将所有这些结合起来,下面列出了在等高线图上执行 Adam 优化并绘制结果的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
# 在测试函数的等高线图上绘制 Adam 搜索的示例 from math import sqrt from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 目标函数的导数 def derivative(x, y): return asarray([x * 2.0, y * 2.0]) # 带有 adam 的梯度下降算法 def adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2, eps=1e-8): solutions = list() # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) score = objective(x[0], x[1]) # 初始化一阶和二阶矩 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降更新 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量构建解 for i in range(bounds.shape[0]): # m(t) = beta1 * m(t-1) + (1 - beta1) * g(t) m[i] = beta1 * m[i] + (1.0 - beta1) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = beta2 * v[i] + (1.0 - beta2) * g[i]**2 # mhat(t) = m(t) / (1 - beta1(t)) mhat = m[i] / (1.0 - beta1**(t+1)) # vhat(t) = v(t) / (1 - beta2(t)) vhat = v[i] / (1.0 - beta2**(t+1)) # x(t) = x(t-1) - alpha * mhat(t) / (sqrt(vhat(t)) + ep) x[i] = x[i] - alpha * mhat / (sqrt(vhat) + eps) # 评估候选点 score = objective(x[0], x[1]) # 跟踪解决方案 solutions.append(x.copy()) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return solutions # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 60 # 步长 alpha = 0.02 # 平均梯度因子 beta1 = 0.8 # 平均梯度平方因子 beta2 = 0.999 # 使用 Adam 执行梯度下降搜索 solutions = adam(objective, derivative, bounds, n_iter, alpha, beta1, beta2) # 以 0.1 为增量均匀采样输入范围 xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') # 将样本绘制为黑色圆圈 solutions = asarray(solutions) pyplot.plot(solutions[:, 0], solutions[:, 1], '.-', color='w') # 显示绘图 pyplot.show() |
运行示例将像以前一样执行搜索,只是在这种情况下,会创建目标函数的等高线图。
在这种情况下,我们可以看到搜索过程中找到的每个解决方案都显示为一个白点,从最优值上方开始,并逐渐靠近图中中心的最优值。
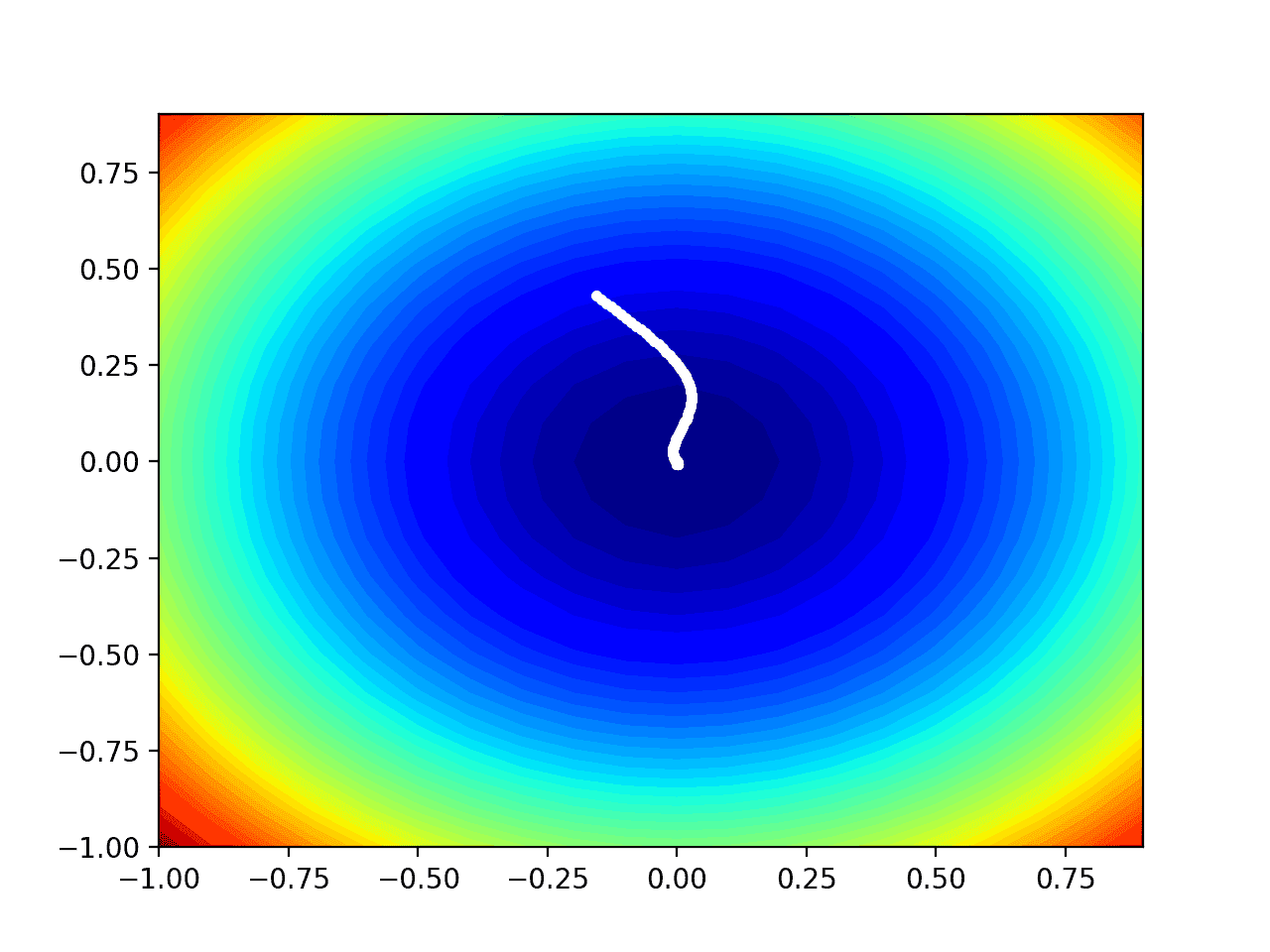
使用 Adam 搜索结果的测试目标函数等高线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- Adam:一种随机优化方法, 2014.
书籍
API
文章
- 梯度下降,维基百科.
- 随机梯度下降,维基百科.
- 梯度下降优化算法综述, 2016.
总结
在本教程中,您学习了如何从头开始开发基于 Adam 优化的梯度下降。
具体来说,你学到了:
- 梯度下降是一种优化算法,它利用目标函数的梯度来导航搜索空间。
- 梯度下降可以通过一种衰减的偏导数平均值,称为 Adam,来更新,以使用每个输入变量的自动自适应步长。
- 如何从头开始实现 Adam 优化算法,并将其应用于目标函数并评估结果。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






如果能使用一个更难的目标函数来测试 Adam 的实现,那就更好了。
好建议!
这次我想专注于算法。
这个优化技术可以在天线设计中实现吗?
也许可以。
也许可以尝试一下。
如果可能用于情感分类吗?
不,您应该为此任务使用神经网络。Adam 可用于训练您的神经网络。
很棒的文章,Jason。我想知道您的书中是否讨论了这些和其他优化算法。
谢谢!
我希望很快能写一本关于优化主题的书。
非常感谢你……
不客气。
Hi Jason,下面的方程是错误的。
x(t) = x(t-1) – alpha * mhat(t) / sqrt(vhat(t)) + eps
由于除法的优先级高于加法,它应该写成
x(t) = x(t-1) – alpha * mhat(t) / (sqrt(vhat(t)) + eps)
谢谢,同意!
幸好只是评论——代码是正确的。
我推荐以下修复
# 以 0.1 为增量均匀采样输入范围
xaxis = arange(bounds[0,0], bounds[0,1]+0.1, 0.1)
yaxis = arange(bounds[1,0], bounds[1,1]+0.1, 0.1)
# 使轴相等
pyplot.axis(‘equal’)
谢谢您的提示!
嗨,Jason,
您是否有 Adam 使用 mini-batch 的示例?例如,您是否会计算每个样本的 2 阶矩向量,然后在批次结束的权重更新之前对它们进行平均(类似于梯度)?或者将每个批次视为一个迭代 WRT t?还是其他什么…?
我认为没有。
凭经验来看,我认为您将项跨多个样本相加/平均。
嗨,Jason,
感谢您这篇精彩的文章。我想知道当目标函数没有解析解时,您将如何进行?正如许多神经网络的情况一样。Adam 在这种情况下如何展开?
再次感谢。
GD 需要梯度。
如果不存在这样的梯度,您可以使用不要求梯度的不同算法,即所谓的直接搜索算法(Nelder Mead 及其同类算法),甚至随机算法(模拟退火、遗传算法及其同类算法)。
如何在 Matlab 中使用 Adam 优化来设计 FIR 滤波器,目标函数为-
J2 = ∑ abs [abs (| Η (ω) | -1) -δp] + ∑ [abs (-δs)]
请帮忙或提供一些参考。
抱歉,我没有 Matlab 的例子。
嗨,Jason,
您的哪本书像上面那样解释了所有优化算法?
还没有关于优化的书,希望很快能有。
我可以使用 ADAM 优化来调整权重。
每次迭代中的每个权重都会被调整。
可能存在一个误差,即预期输出与计算输出(必须使用输入和权重进行计算)之间的差异。
我需要知道误差,因为我需要正确调整(在梯度中,我按误差增量进行调整)。
我不明白 Adam 优化算法如何纠正误差增量。也许这个例子忽略了这一点。
如果我没理解错的话,您提到的误差修正就是公式中的 g(t)。
我认为在 mhat 中是 beta^t 而不是 beta(t)
感谢您的反馈 Marc!您说得对。
我认为在 mhat 中是 beta^t 而不是 beta(t)。
感谢您的反馈 Marc!
James,可能需要稍作更正。Adam 代表自适应矩估计(请参阅论文),其中矩是指统计矩,而不是我们搜索空间中候选点的移动。虽然从语义上讲,移动(Movement)也说得通 😉
感谢您的反馈 Ashutosh!您说得对!
我确信如果您能学习机器学习数学,您也能学到基本的 Latex 数学符号,这样您的网站上这篇以及任何其他博文的可读性都会提高很多。
在关于机器学习的博文中看到“beta1”和“beta2”,这很令人失望,更不用说令人困惑了……
感谢您的反馈 Jake!
您好,感谢您这篇非常好的文章。
我需要您的书的第 5 章,“梯度下降法”,以便在我的文章中使用和引用。
非常感谢。
您好 mb-bahreini… 非常欢迎!
如果你在自己的项目中使用我的代码或材料,请注明来源,包括
作者姓名,例如“Jason Brownlee”。
教程或书籍的标题。
网站名称,例如“Machine Learning Mastery”。
教程或书籍的 URL。
您访问或复制该代码的日期。
例如
Jason Brownlee,Python 机器学习算法,Machine Learning Mastery,网址:https://machinelearning.org.cn/machine-learning-with-python/,访问日期:2018 年 4 月 15 日。
另外,如果您的作品是公开的,请联系我,我很乐意出于普遍兴趣看看它。
信息量很大,James,谢谢。但我正在尝试将该方法应用于最小化离散函数而不是连续函数,而连续函数是可以微分的。有什么方法可以做到吗?
您非常欢迎 John!以下讨论可能会提供更多说明
https://stackoverflow.com/questions/17864474/how-to-minimize-a-function-with-discrete-variable-values-in-scipy
我认为 Adam 代表自适应矩(不是移动)。该论文指出:“Adam 这个名字
源自自适应矩估计。”(https://arxiv.org/pdf/1412.6980.pdf)
感谢您的反馈 Kevin!
score = objective(x[0], x[1]),这里的 x[0]和 x[1]分别代表什么?
您好 luxiyang…它们代表传递给函数的 x 和 y 的值
# 目标函数 def objective(x, y): return x**2.0 + y**2.0
您能否为代码添加缩进?
否则页面非常好,但缺乏缩进使得代码难以阅读。
感谢您的建议和反馈 Beginner!