循环神经网络及其数学原理简介

在处理序列数据或时间序列数据时，传统的前馈网络无法用于学习和预测。需要一种机制来保留过去或历史信息以预测未来值。循环神经网络（RNN）是传统前馈人工神经网络的一个变体，它可以处理序列数据，并且可以被训练以保留过去的知识。

完成本教程后，您将了解：

• 循环神经网络
• 展开RNN是什么意思
• RNN中的权重如何更新
• 各种RNN架构

开始您的项目，阅读我的书 《构建Transformer模型及其注意力机制》。它提供了自学教程和可运行代码，指导您构建一个能够
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...

让我们开始吧。

循环神经网络及其背后数学原理的介绍。图片作者：Mehreen Saeed，部分权利保留。

教程概述

本教程分为两部分；它们是

1. RNN的工作原理
   1. 时序展开
   2. 时序反向传播算法
2. 不同的RNN架构和变体

先决条件

本教程假设您已经熟悉了人工神经网络和反向传播算法。如果不熟悉，您可以参阅Stefania Cristina撰写的这篇非常棒的教程 《演算在实践：神经网络》。该教程还解释了如何使用基于梯度的反向传播算法来训练神经网络。

什么是循环神经网络

循环神经网络（RNN）是一种特殊类型的人工神经网络，经过改编以处理时间序列数据或涉及序列的数据。普通的前馈神经网络仅用于彼此独立的数据点。但是，如果我们有序列数据，其中一个数据点依赖于前一个数据点，我们就需要修改神经网络以包含这些数据点之间的依赖关系。RNN具有“记忆”的概念，可以帮助它们存储先前输入的状​​态或信息，以生成序列的下一个输出。

展开循环神经网络

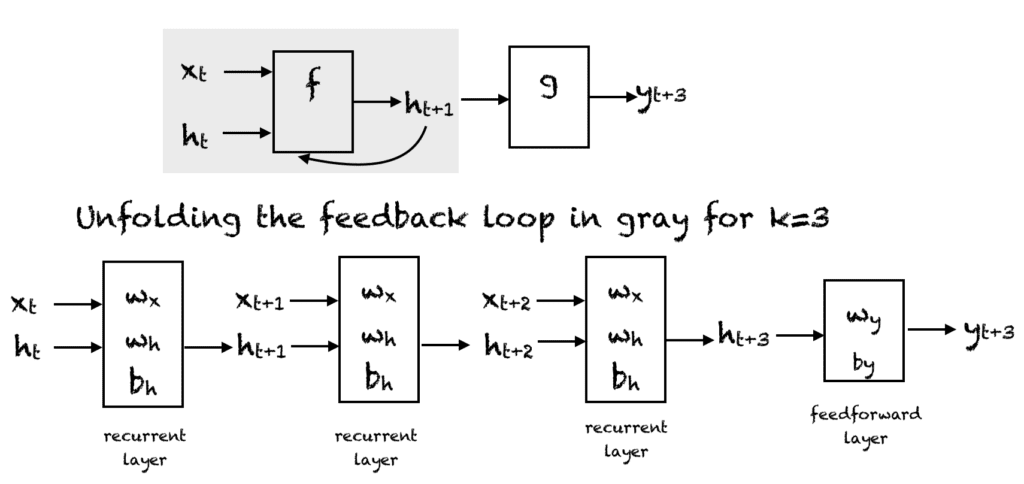
循环神经网络。压缩表示（上），展开的网络（下）。

一个简单的RNN有一个反馈循环，如上图的第一个图所示。灰色矩形框中的反馈循环可以展开成三个时间步，得到上图的第二个网络。当然，您可以更改架构，使网络展开 $k$ 个时间步。图中使用了以下符号：

• $x_t \in R$ 是时间步 $t$ 的输入。为简单起见，我们假设 $x_t$ 是一个具有单个特征的标量值。您可以将此思想扩展到 $d$ 维特征向量。
• $y_t \in R$ 是网络在时间步 $t$ 的输出。我们可以在网络中产生多个输出，但在此示例中，我们假设只有一个输出。
• $h_t \in R^m$ 向量存储时间 $t$ 的隐藏单元/状态的值。这也称为当前上下文。 $m$ 是隐藏单元的数量。 $h_0$ 向量初始化为零。
• $w_x \in R^{m}$ 是与循环层中输入相关的权重
• $w_h \in R^{mxm}$ 是与循环层中隐藏单元相关的权重
• $w_y \in R^m$ 是与隐藏单元到输出单元相关的权重
• $b_h \in R^m$ 是与循环层相关的偏置
• $b_y \in R$ 是与前馈层相关的偏置

在每个时间步，我们可以将网络展开 $k$ 个时间步，以获得时间步 $k+1$ 的输出。展开的网络非常类似于前馈神经网络。展开网络中的矩形框表示正在进行的操作。因此，例如，使用激活函数 f

因此，在RNN的前馈过程中，网络计算隐藏单元的值以及 $k$ 个时间步后的输出。网络相关的权重是时间共享的。每个循环层有两个权重集：一个用于输入，第二个用于隐藏单元。最后一个前馈层计算第 $k$ 个时间步的最终输出，这与传统前馈网络的普通层一样。

激活函数

我们可以在循环神经网络中使用任何我们想要的激活函数。常见的选择是：

• Sigmoid函数：$\frac{1}{1+e^{-x}}$
• Tanh函数：$\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$
• Relu函数：max$(0,x)$

训练循环神经网络

人工神经网络的反向传播算法进行了修改，以包括时序展开来训练网络的权重。该算法基于计算梯度向量，并简称为时序反向传播或BPTT算法。训练的伪代码如下。 $k$ 的值可以由用户选择进行训练。在下面的伪代码中，$p_t$ 是时间步 t 的目标值。

1. 重复，直到停止标准满足
   1. 将所有 $h$ 设置为零。
   2. 重复 t = 0 到 n-k
      1. 在前向展开的网络上，通过 $k$ 个时间步来前向传播网络，以计算所有 $h$ 和 $y$
      2. 计算误差为：$e = y_{t+k}-p_{t+k}$
      3. 将误差反向传播到展开的网络中，并更新权重

RNN的类型

循环神经网络有不同的类型，具有不同的架构。例如：

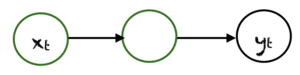
一对一

这里有一个单一的 $(x_t, y_t)$ 对。传统的神经网络采用一对一的架构。

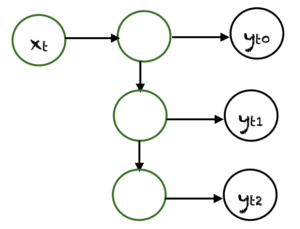
一对多

在一对多网络中， $x_t$ 的单个输入可以产生多个输出，例如 $(y_{t0}, y_{t1}, y_{t2})$。音乐生成是一个应用一对多网络的领域示例。

多对一

在这种情况下，来自不同时间步的多个输入产生一个单一的输出。例如，$(x_t, x_{t+1}, x_{t+2})$ 可以产生一个输出 $y_t$。这类网络应用于情感分析或情绪检测，其中类别标签取决于一系列单词。

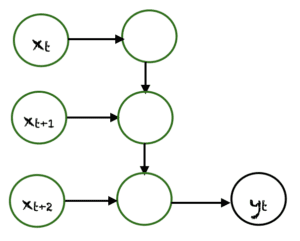
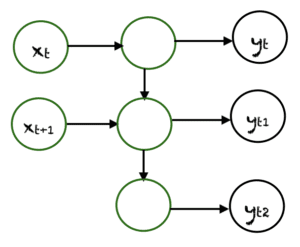
多对多

多对多的情况有很多种。上面展示了一个例子，其中两个输入产生三个输出。多对多网络应用于机器翻译，例如英译法或法译英翻译系统。

RNN的优点和缺点

RNN具有多种优点，例如：

• 能够处理序列数据
• 能够处理可变长度的输入
• 能够存储或“记住”历史信息

缺点是：

• 计算可能非常缓慢。
• 网络在做决策时未考虑未来的输入。
• 梯度消失问题，用于计算权重更新的梯度可能变得非常接近于零，从而阻止网络学习新的权重。网络越深，这个问题就越明显。

不同的RNN架构

在机器学习问题中有许多不同的RNN变体被实际应用。

双向循环神经网络（BRNN）

在BRNN中，来自未来时间步的输入被用于提高网络的准确性。这就像知道句子的第一个和最后一个词来预测中间的词。

门控循环单元（GRU）

这些网络旨在解决梯度消失问题。它们有一个重置门和更新门。这些门决定了要为未来预测保留哪些信息。

长短期记忆（LSTM）

LSTM 也旨在解决RNN中的梯度消失问题。LSTM使用三个门：输入门、输出门和遗忘门。与GRU类似，这些门决定要保留哪些信息。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• Wei Di, Anurag Bhardwaj, and Jianing Wei 著《深度学习基础》
• Ian Goodfellow, Joshua Bengio, and Aaron Courville 著《深度学习》。

文章

• BPTT维基百科文章
• 深度学习循环神经网络算法详解
• 时间反向传播简明介绍

总结

在本教程中，您了解了循环神经网络及其各种架构。

具体来说，你学到了：

• 循环神经网络如何处理序列数据
• 循环神经网络的时序展开
• 什么是时序反向传播
• RNN的优缺点
• 各种RNN的架构和变体

Do you have any questions about RNNs discussed in this post? Ask your questions in the comments below, and I will do my best to answer.

学习 Transformer 和注意力！

教您的深度学习模型阅读句子

...使用带有注意力的 Transformer 模型

在我的新电子书中探索如何实现
使用注意力机制构建 Transformer 模型

它提供了自学教程和可运行代码，指导您构建一个可以
将句子从一种语言翻译成另一种语言的完整 Transformer 模型...

为理解人类语言提供神奇力量
您的项目

查看内容