微分在神经网络中的应用

微分法则是机器学习算法中的重要工具。特别是在神经网络中，梯度下降算法依赖于由微分计算出的量——梯度。

在本教程中，我们将了解反向传播技术如何在神经网络中用于寻找梯度。

完成本教程后，您将了解：

• 什么是全微分和全导数？
• 如何在神经网络中计算全导数？
• 反向传播如何帮助计算全导数？

让我们开始吧

微分在神经网络中的应用
照片作者：Freeman Zhou，部分权利保留。

教程概述

本教程分为5个部分，它们是：

1. 全微分与全导数
2. 多层感知机模型的代数表示
3. 通过反向传播找到梯度
4. 梯度方程的矩阵形式
5. 实现反向传播

全微分与全导数

对于像 $f(x)$ 这样的函数，我们将其导数表示为 $f'(x)$ 或 $\frac{df}{dx}$。但对于多变量函数，例如 $f(u,v)$，我们有 $f$ 相对于 $u$ 的偏导数，记为 $\frac{\partial f}{\partial u}$，或有时写为 $f_u$。偏导数是通过对 $f$ 相对于 $u$ 进行微分而获得的，同时假定另一个变量 $v$ 是常数。因此，我们使用 $\partial$ 而不是 $d$ 作为微分符号来表示区别。

但是，如果 $f(u,v)$ 中的 $u$ 和 $v$ 都是 $x$ 的函数呢？换句话说，我们可以写成 $u(x)$ 和 $v(x)$ 以及 $f(u(x), v(x))$。所以 $x$ 决定了 $u$ 和 $v$ 的值，进而决定了 $f(u,v)$。在这种情况下，询问 $\frac{df}{dx}$ 是什么是很正常的，因为 $f$ 最终由 $x$ 决定。

这就是全导数的概念。事实上，对于多变量函数 $f(t,u,v)=f(t(x),u(x),v(x))$，我们总有
$$
\frac{df}{dx} = \frac{\partial f}{\partial t}\frac{dt}{dx} + \frac{\partial f}{\partial u}\frac{du}{dx} + \frac{\partial f}{\partial v}\frac{dv}{dx}
$$
上面的表示法称为全导数，因为它是一系列偏导数的总和。本质上，它是应用链式法则来查找微分。

如果我们去掉上面方程中的 $dx$ 部分，我们得到的是 $f$ 相对于 $x$ 的近似变化，即：
$$
df = \frac{\partial f}{\partial t}dt + \frac{\partial f}{\partial u}du + \frac{\partial f}{\partial v}dv
$$
我们将此表示法称为全微分。

多层感知机模型的代数表示

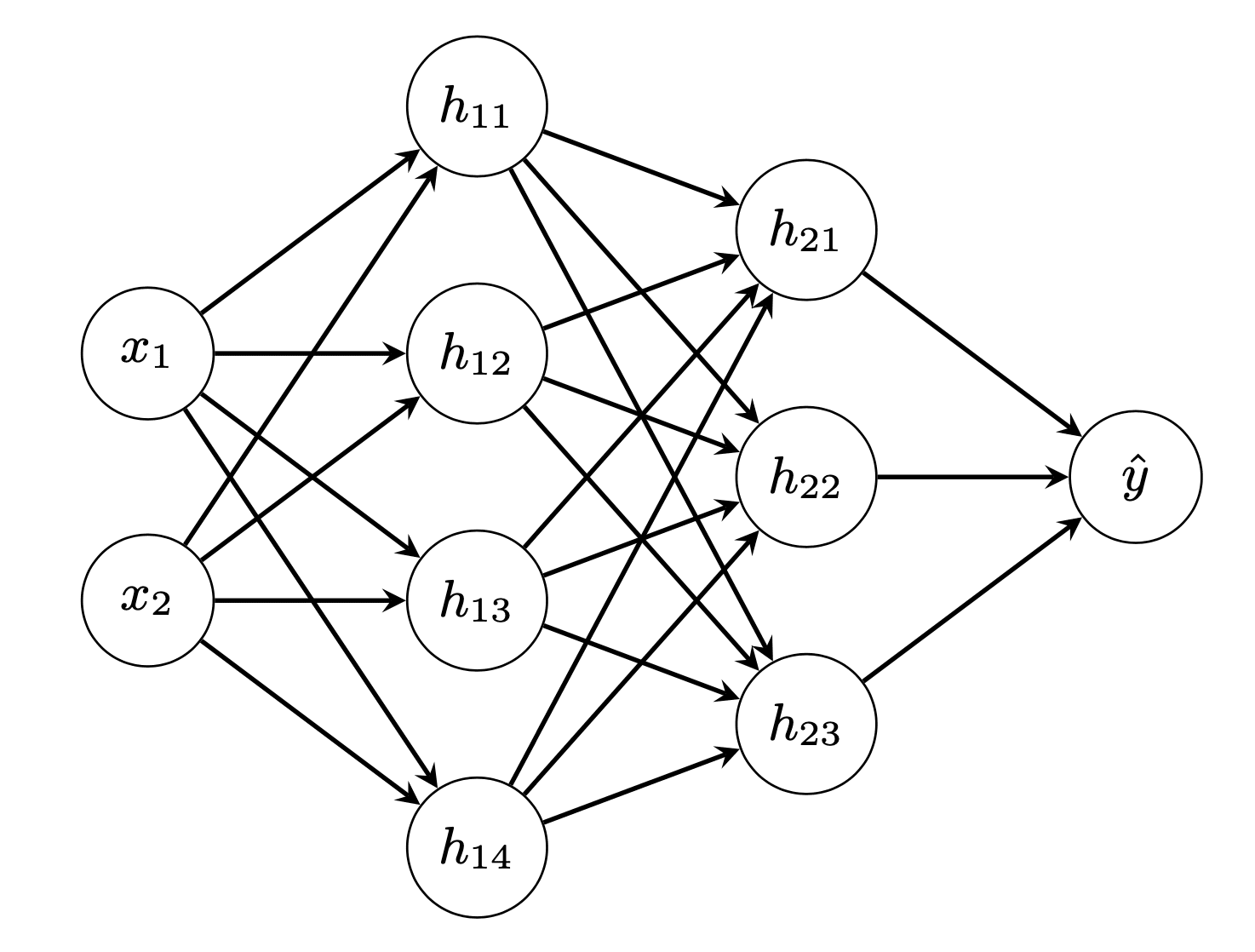
考虑网络

神经网络的一个例子。来源：https://commons.wikimedia.org/wiki/File:Multilayer_Neural_Network.png

这是一个简单的全连接四层神经网络。我们称输入层为第0层，两个隐藏层为第1层和第2层，输出层为第3层。在此图中，我们看到有 $n_0=3$ 个输入单元，第一隐藏层有 $n_1=4$ 个单元，第二个隐藏层有 $n_2=2$ 个单元。有 $n_3=2$ 个输出单元。

如果我们用 $x_i$ ($i=1,\cdots,n_0$) 表示网络的输入，用 $\hat{y}_i$ ($i=1,\cdots,n_3$) 表示网络的输出，那么我们可以写成：

$$
\begin{aligned}
h_{1i} &= f_1(\sum_{j=1}^{n_0} w^{(1)}_{ij} x_j + b^{(1)}_i) & \text{对于 } i &= 1,\cdots,n_1\\
h_{2i} &= f_2(\sum_{j=1}^{n_1} w^{(2)}_{ij} h_{1j} + b^{(2)}_i) & i &= 1,\cdots,n_2\\
\hat{y}_i &= f_3(\sum_{j=1}^{n_2} w^{(3)}_{ij} h_{2j} + b^{(3)}_i) & i &= 1,\cdots,n_3
\end{aligned}
$$

这里，第 $i$ 层的激活函数表示为 $f_i$。第一隐藏层的输出表示为第 $i$ 个单元的 $h_{1i}$。类似地，第二隐藏层的输出表示为 $h_{2i}$。第 $k$ 层第 $i$ 个单元的权重和偏差分别表示为 $w^{(k)}_{ij}$ 和 $b^{(k)}_i$。

在上面，我们可以看到第 $k-1$ 层的输出将馈入第 $k$ 层。因此，虽然 $\hat{y}_i$ 被表示为 $h_{2j}$ 的函数，但 $h_{2i}$ 也是 $h_{1j}$ 的函数，而 $h_{1j}$ 又可以表示为 $x_j$ 的函数。

以上描述了神经网络的代数方程构建。训练神经网络还需要指定一个*损失函数*，以便我们在训练循环中最小化它。根据应用的不同，我们通常使用交叉熵来处理分类问题，或使用均方误差来处理回归问题。目标变量为 $y_i$，均方误差损失函数指定为：
$$
L = \sum_{i=1}^{n_3} (y_i-\hat{y}_i)^2
$$

通过反向传播找到梯度

在上述构建中，$x_i$ 和 $y_i$ 来自数据集。神经网络的参数是 $w$ 和 $b$。而激活函数 $f_i$ 是设计好的，各层的输出 $h_{1i}$、$h_{2i}$ 和 $\hat{y}_i$ 是因变量。在训练神经网络时，我们的目标是在每次迭代中更新 $w$ 和 $b$，即根据梯度下降更新规则：
$$
\begin{aligned}
w^{(k)}_{ij} &= w^{(k)}_{ij} – \eta \frac{\partial L}{\partial w^{(k)}_{ij}} \\
b^{(k)}_{i} &= b^{(k)}_{i} – \eta \frac{\partial L}{\partial b^{(k)}_{i}}
\end{aligned}
$$
其中 $\eta$ 是梯度下降的学习率参数。

从 $L$ 的方程我们知道 $L$ 不直接依赖于 $w^{(k)}_{ij}$ 或 $b^{(k)}_i$，而是依赖于 $\hat{y}_i$。然而，$\hat{y}_i$ 最终可以表示为 $w^{(k)}_{ij}$ 或 $b^{(k)}_i$ 的函数。让我们逐一看看第 $k$ 层的权重和偏差如何与输出层 $\hat{y}_i$ 相关联。

我们从损失指标开始。如果我们考虑单个数据点的损失，我们有：
$$
\begin{aligned}
L &= \sum_{i=1}^{n_3} (y_i-\hat{y}_i)^2\\
\frac{\partial L}{\partial \hat{y}_i} &= 2(y_i – \hat{y}_i) & \text{对于 } i &= 1,\cdots,n_3
\end{aligned}
$$
这里我们看到损失函数依赖于所有输出 $\hat{y}_i$，因此我们可以找到一个偏导数 $\frac{\partial L}{\partial \hat{y}_i}$。

现在我们来看输出层：
$$
\begin{aligned}
\hat{y}_i &= f_3(\sum_{j=1}^{n_2} w^{(3)}_{ij} h_{2j} + b^{(3)}_i) & \text{对于 }i &= 1,\cdots,n_3 \\
\frac{\partial L}{\partial w^{(3)}_{ij}} &= \frac{\partial L}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial w^{(3)}_{ij}} & i &= 1,\cdots,n_3;\ j=1,\cdots,n_2 \\
&= \frac{\partial L}{\partial \hat{y}_i} f’_3(\sum_{j=1}^{n_2} w^{(3)}_{ij} h_{2j} + b^{(3)}_i)h_{2j} \\
\frac{\partial L}{\partial b^{(3)}_i} &= \frac{\partial L}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial b^{(3)}_i} & i &= 1,\cdots,n_3 \\
&= \frac{\partial L}{\partial \hat{y}_i}f’_3(\sum_{j=1}^{n_2} w^{(3)}_{ij} h_{2j} + b^{(3)}_i)
\end{aligned}
$$
因为第3层的权重 $w^{(3)}_{ij}$ 应用于输入 $h_{2j}$，并且仅影响输出 $\hat{y}_i$。因此，我们可以将导数 $\frac{\partial L}{\partial w^{(3)}_{ij}}$ 写成两个导数的乘积 $\frac{\partial L}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial w^{(3)}_{ij}}$。对于偏差 $b^{(3)}_i$ 也是类似的情况。在上面，我们利用了 $\frac{\partial L}{\partial \hat{y}_i}$，这是我们之前推导过的。

但实际上，我们也可以写出 $L$ 相对于第二层输出 $h_{2j}$ 的偏导数。它不用于更新第3层的权重和偏差，但我们稍后会看到它的重要性。
$$
\begin{aligned}
\frac{\partial L}{\partial h_{2j}} &= \sum_{i=1}^{n_3}\frac{\partial L}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial h_{2j}} & \text{对于 }j &= 1,\cdots,n_2 \\
&= \sum_{i=1}^{n_3}\frac{\partial L}{\partial \hat{y}_i}f’_3(\sum_{j=1}^{n_2} w^{(3)}_{ij} h_{2j} + b^{(3)}_i)w^{(3)}_{ij}
\end{aligned}
$$
这个比较有趣，与之前的偏导数不同。请注意，$h_{2j}$ 是第二层的输出。第二层的每一个输出都会影响第三层的输出 $\hat{y}_i$。因此，为了找到 $\frac{\partial L}{\partial h_{2j}}$，我们需要将第三层的每个输出加起来。因此，上面的方程中出现了求和符号。我们可以将 $\frac{\partial L}{\partial h_{2j}}$ 视为全导数，其中我们应用链式法则 $\frac{\partial L}{\partial \hat{y}_i}\frac{\partial \hat{y}_i}{\partial h_{2j}}$ 对每个输出 $i$ 求和。

如果我们退回到第二层，我们可以类似地推导出导数：
$$
\begin{aligned}
h_{2i} &= f_2(\sum_{j=1}^{n_1} w^{(2)}_{ij} h_{1j} + b^{(2)}_i) & \text{对于 }i &= 1,\cdots,n_2\\
\frac{\partial L}{\partial w^{(2)}_{ij}} &= \frac{\partial L}{\partial h_{2i}}\frac{\partial h_{2i}}{\partial w^{(2)}_{ij}} & i&=1,\cdots,n_2;\ j=1,\cdots,n_1 \\
&= \frac{\partial L}{\partial h_{2i}}f’_2(\sum_{j=1}^{n_1} w^{(2)}_{ij} h_{1j} + b^{(2)}_i)h_{1j} \\
\frac{\partial L}{\partial b^{(2)}_i} &= \frac{\partial L}{\partial h_{2i}}\frac{\partial h_{2i}}{\partial b^{(2)}_i} & i &= 1,\cdots,n_2 \\
&= \frac{\partial L}{\partial h_{2i}}f’_2(\sum_{j=1}^{n_1} w^{(2)}_{ij} h_{1j} + b^{(2)}_i) \\
\frac{\partial L}{\partial h_{1j}} &= \sum_{i=1}^{n_2}\frac{\partial L}{\partial h_{2i}}\frac{\partial h_{2i}}{\partial h_{1j}} & j&= 1,\cdots,n_1 \\
&= \sum_{i=1}^{n_2}\frac{\partial L}{\partial h_{2i}}f’_2(\sum_{j=1}^{n_1} w^{(2)}_{ij} h_{1j} + b^{(2)}_i) w^{(2)}_{ij}
\end{aligned}
$$

在上面的方程中，我们重用了之前推导出的 $\frac{\partial L}{\partial h_{2i}}$。同样，这个导数是通过链式法则的多个乘积的和来计算的。此外，与之前类似，我们也推导出了 $\frac{\partial L}{\partial h_{1j}}$。它不用于训练 $w^{(2)}_{ij}$ 或 $b^{(2)}_i$，但将用于之前的层。所以对于第1层，我们有：

$$
\begin{aligned}
h_{1i} &= f_1(\sum_{j=1}^{n_0} w^{(1)}_{ij} x_j + b^{(1)}_i) & \text{对于 } i &= 1,\cdots,n_1\\
\frac{\partial L}{\partial w^{(1)}_{ij}} &= \frac{\partial L}{\partial h_{1i}}\frac{\partial h_{1i}}{\partial w^{(1)}_{ij}} & i&=1,\cdots,n_1;\ j=1,\cdots,n_0 \\
&= \frac{\partial L}{\partial h_{1i}}f’_1(\sum_{j=1}^{n_0} w^{(1)}_{ij} x_j + b^{(1)}_i)x_j \\
\frac{\partial L}{\partial b^{(1)}_i} &= \frac{\partial L}{\partial h_{1i}}\frac{\partial h_{1i}}{\partial b^{(1)}_i} & i&=1,\cdots,n_1 \\
&= \frac{\partial L}{\partial h_{1i}}f’_1(\sum_{j=1}^{n_0} w^{(1)}_{ij} x_j + b^{(1)}_i)
\end{aligned}
$$

这样就完成了使用梯度下降算法训练神经网络所需的所有导数。

回想一下我们是如何推导上述公式的：我们首先从损失函数 $L$ 开始，然后按层相反的顺序逐个计算导数。我们写下第 $k$ 层的导数，并将其用于第 $k-1$ 层的导数。虽然从输入 $x_i$ 开始正向计算输出 $\hat{y}_i$，但梯度计算是按相反顺序进行的。因此被称为“反向传播”。

梯度方程的矩阵形式

虽然上面我们没有使用它，但用向量和矩阵写方程会更清晰。我们可以将层和输出重写为：
$$
\mathbf{a}_k = f_k(\mathbf{z}_k) = f_k(\mathbf{W}_k\mathbf{a}_{k-1}+\mathbf{b}_k)
$$
其中 $\mathbf{a}_k$ 是第 $k$ 层输出的向量，假设 $\mathbf{a}_0=\mathbf{x}$ 是输入向量，$\mathbf{a}_3=\hat{\mathbf{y}}$ 是输出向量。为了方便表示，我们也用 $\mathbf{z}_k = \mathbf{W}_k\mathbf{a}_{k-1}+\mathbf{b}_k$ 来表示。

在这种表示法下，我们可以将 $\frac{\partial L}{\partial\mathbf{a}_k}$ 表示为向量（$\mathbf{z}_k$ 和 $\mathbf{b}_k$ 也是如此），将 $\frac{\partial L}{\partial\mathbf{W}_k}$ 表示为矩阵。然后，如果已知 $\frac{\partial L}{\partial\mathbf{a}_k}$，我们有：
$$
\begin{aligned}
\frac{\partial L}{\partial\mathbf{z}_k} &= \frac{\partial L}{\partial\mathbf{a}_k}\odot f_k'(\mathbf{z}_k) \\
\frac{\partial L}{\partial\mathbf{W}_k} &= \left(\frac{\partial L}{\partial\mathbf{z}_k}\right)^\top \cdot \mathbf{a}_k \\
\frac{\partial L}{\partial\mathbf{b}_k} &= \frac{\partial L}{\partial\mathbf{z}_k} \\
\frac{\partial L}{\partial\mathbf{a}_{k-1}} &= \left(\frac{\partial\mathbf{z}_k}{\partial\mathbf{a}_{k-1}}\right)^\top\cdot\frac{\partial L}{\partial\mathbf{z}_k} = \mathbf{W}_k^\top\cdot\frac{\partial L}{\partial\mathbf{z}_k}
\end{aligned}
$$
其中 $\frac{\partial\mathbf{z}_k}{\partial\mathbf{a}_{k-1}}$ 是一个雅可比矩阵，因为 $\mathbf{z}_k$ 和 $\mathbf{a}_{k-1}$ 都是向量，而这个雅可比矩阵恰好是 $\mathbf{W}_k$。

实现反向传播

我们需要矩阵形式的方程，因为它们能让我们的代码更简洁，并避免大量循环。我们来看看如何将这些方程转换为代码，并使用 numpy 从头开始实现一个用于分类的多层感知机模型。

我们需要实现的第一个东西是激活函数和损失函数。两者都需要是可微分的函数，否则我们的梯度下降过程将无法工作。如今，在隐藏层中使用 ReLU 激活，在输出层中使用 Sigmoid 激活是很常见的。我们将它们定义为函数（假设输入为 numpy 数组）以及它们的微分。

我们特意将 Sigmoid 函数的输入限制在 -500 到 +500 之间，以避免溢出。否则，这些函数就很简单了。然后对于分类，我们关心准确率，但准确率函数是不可微分的。因此，我们使用交叉熵函数作为训练的损失。

在上面，我们假设输出和目标变量是 numpy 中的行向量。因此，我们使用点积运算符 @ 来计算总和，并除以输出的元素数量。请注意，此设计旨在计算**批量**样本的**平均交叉熵**。

然后我们可以实现我们的多层感知机模型。为了便于阅读，我们希望通过提供每层神经元数量以及层激活函数来创建模型。但同时，我们还需要激活函数的微分以及损失函数的微分来进行训练。损失函数本身虽然不是必需的，但对我们跟踪进度很有用。我们创建一个类来封装整个模型，并根据以下公式定义每一层 $k$：
$$
\mathbf{a}_k = f_k(\mathbf{z}_k) = f_k(\mathbf{a}_{k-1}\mathbf{W}_k+\mathbf{b}_k)
$

此类的变量 z、W、b 和 a 用于前向传播，而变量 dz、dW、db 和 da 是它们各自的梯度，将在反向传播中计算。所有这些变量都表示为 numpy 数组。

正如我们稍后将看到的，我们将使用 scikit-learn 生成的数据来测试我们的模型。因此，我们将看到我们的数据是形状为“(样本数, 特征数)”的 numpy 数组。因此，每个样本在矩阵中都表示为一行，并且在 forward() 函数中，权重矩阵被右乘到该层到每个输入 a。虽然每个层的激活函数和维度可能不同，但过程是相同的。因此，我们在 forward() 函数中通过循环将神经网络的输入 x 转换为其输出。网络的输出只是最后一层的输出。

为了训练网络，我们需要在每次前向传播后运行反向传播。反向传播是从输出层到输入层计算每一层的权重和偏置的梯度。利用上面推导的方程，反向传播函数实现为：

这里唯一的区别是，我们计算 db 不是针对一个训练样本，而是针对整个批次。由于损失函数是跨批次平均的交叉熵，因此我们通过对样本进行平均来计算 db。

到此为止，我们完成了模型。update() 函数仅使用梯度下降更新规则，通过反向传播找到的梯度来更新参数 W 和 b。

为了测试我们的模型，我们利用 scikit-learn 来生成一个分类数据集。

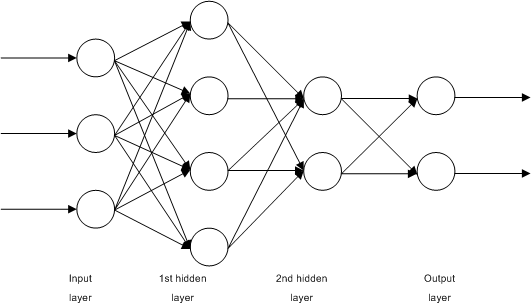
然后我们构建模型：输入是二维的，输出是一维的（逻辑回归）。我们设置两个隐藏层，分别有 4 个和 3 个神经元。

我们看到，在随机权重下，准确率为 50%。

现在我们来训练网络。为了简单起见，我们采用全批量梯度下降和固定学习率。

输出如下：

虽然不是完美的，但我们看到了训练带来的改进。至少在上面的例子中，我们在迭代 145 次时可以看到准确率提高到 80% 以上，但随后我们看到模型发散了。这可以通过降低学习率来改进，而我们上面没有实现这一点。尽管如此，这还是展示了我们如何通过反向传播和链式法则来计算梯度。

完整代码如下：

延伸阅读

反向传播算法是所有神经网络训练的核心，无论你使用何种梯度下降算法的变体。像本书这样的教科书对此进行了介绍：

• Deep Learning, by Ian Goodfellow, Yoshua Bengio, and Aaron Courville, 2016.
  (https://www.amazon.com/dp/0262035618)

以前也从头开始实现了神经网络，没有讨论数学，它更详细地解释了步骤。

• 如何用 Python 从零开始编写带有反向传播的神经网络

总结

在本教程中，您学习了如何将微分应用于神经网络的训练。

具体来说，你学到了：

• 什么是全微分以及如何将其表示为偏微分之和
• 如何将神经网络表示为方程并通过微分推导梯度
• 反向传播如何帮助我们表达神经网络中各层的梯度
• 如何将梯度转换为代码以构建神经网络模型

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容