导数的应用

导数定义了一个变量相对于另一个变量的变化率。 

这是一个非常重要的概念，在许多应用中都非常有用：在日常生活中，导数可以告诉你你的驾驶速度，或者帮助你预测股市的波动；在机器学习中，导数对于函数优化至关重要。 

本教程将探讨导数的不同应用，从更熟悉的开始，然后转向机器学习。我们将更仔细地研究导数告诉我们关于我们正在研究的不同函数的信息。 

在本教程中，您将发现导数的不同应用。 

完成本教程后，您将了解：

• 导数可以应用于我们身边遇到的现实生活问题。 
• 导数对于机器学习中的函数优化至关重要。 

让我们开始吧。 

导数的应用
图片由 Devon Janse van Rensburg 提供，部分权利保留。

教程概述

本教程分为两部分；它们是

• 导数在现实生活中的应用
• 导数在优化算法中的应用

导数在现实生活中的应用

我们已经看到导数模拟了变化率。 

导数回答了“多快？”、“多陡？”和“多敏感？”等问题。这些都是关于某种形式的变化率的问题。 

– 第141页，《无限力量》，2019年。

这种变化率用 ????y / ????x 表示，从而定义了因变量 ????y 相对于自变量 ????x 的变化。

让我们从我们身边最熟悉的导数应用之一开始。 

每次你开车时，你都会遇到微分。 

– 第178页，《数学与科学微积分入门》，2016年。

当我们说一辆车以每小时100公里的速度行驶时，我们就已经说明了它的变化率。我们经常使用的常用术语是速度或速率，尽管最好我们先区分两者。

在日常生活中，当我们描述一个运动物体的变化率时，我们经常互换使用速度和速率。然而，这在数学上是不正确的，因为速度总是正的，而速率引入了方向的概念，因此可以表现为正值和负值。因此，在接下来的解释中，我们将把速率视为更技术性的概念，定义为

速率 = ????y / ????t

这意味着速率表示汽车位置 ????y 在时间间隔 ????t 内的变化。换句话说，速率是位置相对于时间的一阶导数。 

汽车的速率可以保持不变，例如汽车一直以每小时100公里的速度匀速行驶，或者它可以随时间变化。在后一种情况下，这意味着速率函数本身随时间变化，或者简单地说，汽车可以被认为在加速。加速度定义为速度v 的一阶导数，以及位置y 相对于时间的二阶导数

加速度 = ????v / ????t = ????²y / ????t²

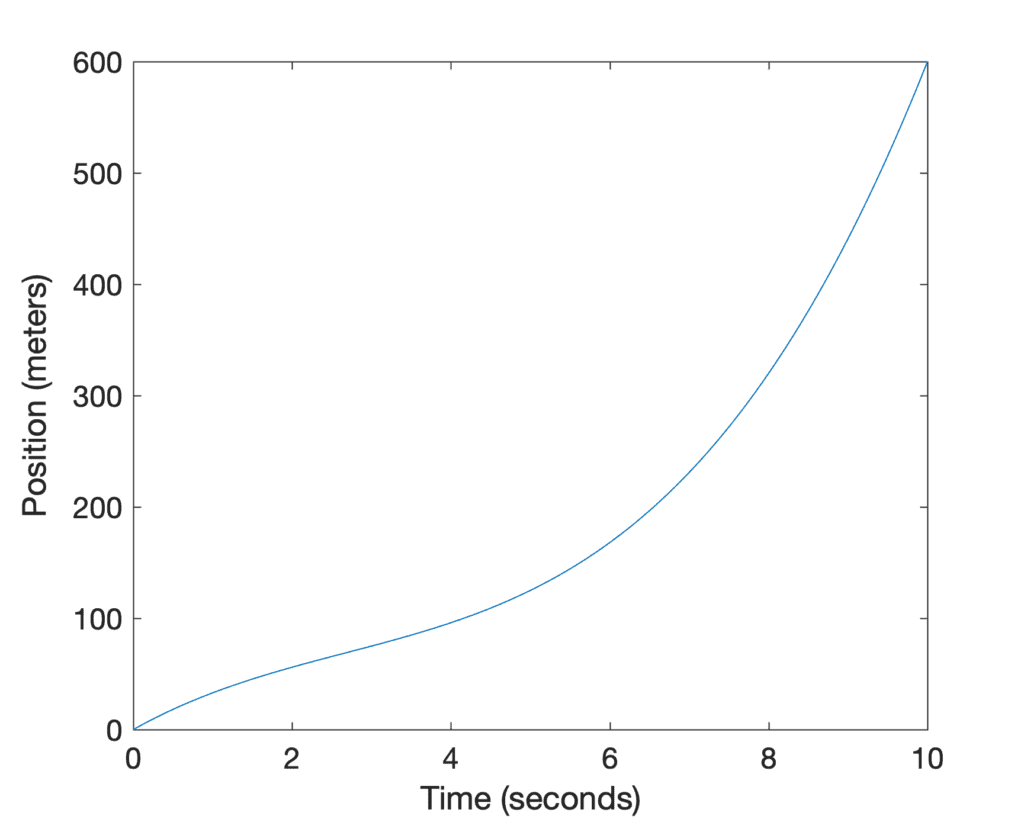
我们可以绘制位置、速率和加速度曲线来更好地可视化它们。假设汽车的位置是关于时间的一个函数，表示为y(t) = t³ – 8t² + 40t

汽车位置与时间的关系图

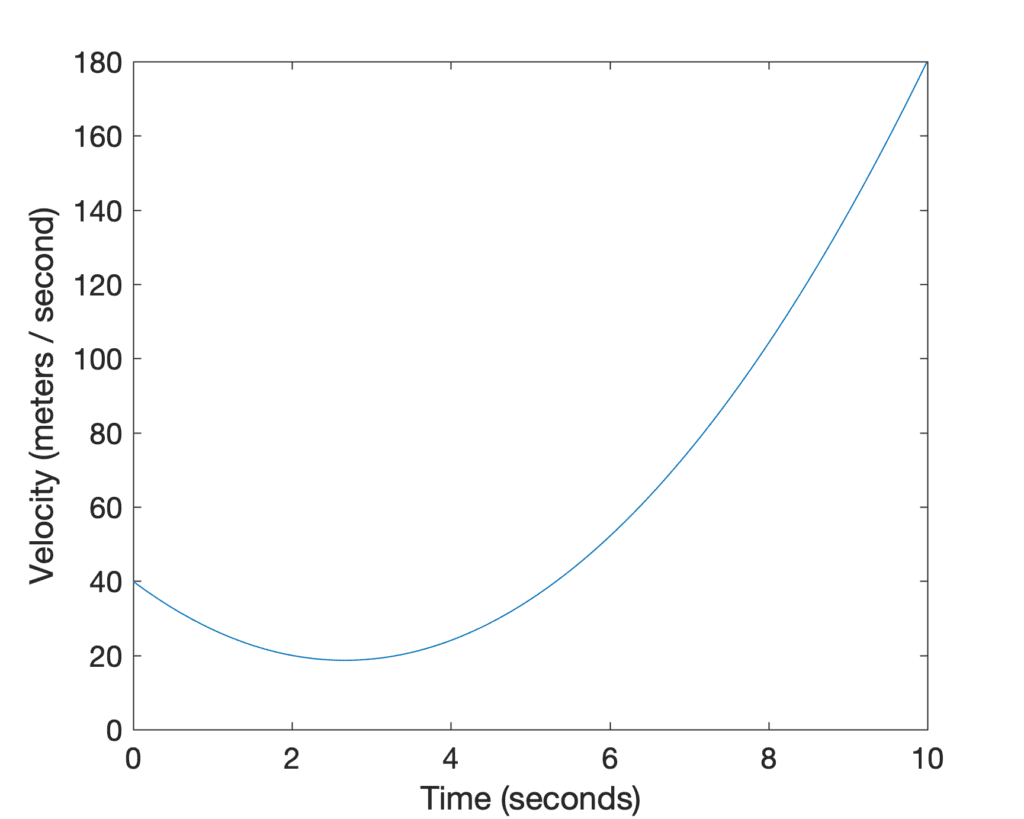
图表显示，汽车在旅程开始时位置变化缓慢，直到大约 t = 2.7 秒时速度略有下降，此时其变化率开始加快并一直增加到旅程结束。这由汽车速率图所示

汽车速率与时间的关系图

请注意，汽车在整个旅程中保持正速率，这是因为它从未改变方向。因此，如果我们想象自己坐在这辆行驶的汽车里，速度计显示的将是我们刚刚在速率图上绘制的值（因为速率始终为正，否则我们将不得不找到速率的绝对值来计算速度）。如果我们应用幂法则对y(t)求导，我们会发现速率由以下函数定义

v(t) = y’(t) = 3t² – 16t + 40

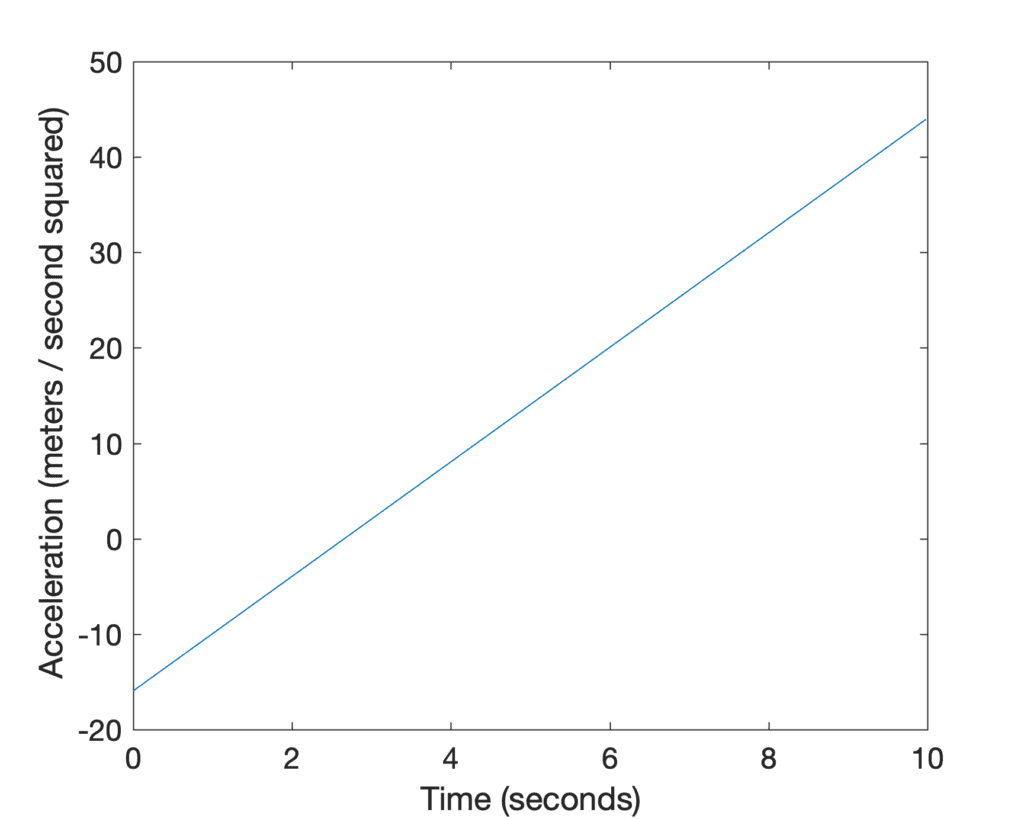
我们也可以绘制加速度图

汽车加速度与时间的关系图

我们发现该图在时间间隔t = [0, 2.7) 秒内以负加速度为特征。这是因为加速度是速率的导数，并且在该时间间隔内汽车的速率正在减小。如果我们再次应用幂法则对v(t)求导，我们会发现加速度由以下函数定义

a(t) = v’(t) = 6t – 16

将所有函数放在一起，我们得到以下

y(t) = t³ – 8t² + 40t

v(t) = y’(t) = 3t² – 16t + 40

a(t) = v’(t) = 6t – 16

如果我们代入t = 10秒，我们可以使用这三个函数来发现，在旅程结束时，汽车已行驶600米，速度为180米/秒，加速度为44米/秒²。我们可以验证所有这些值都与我们刚刚绘制的图表一致。 

我们将这个特定的例子放在寻找汽车速度和加速度的上下文中。但是，正如我们在这个特定例子中所做的那样，有大量的现实生活现象会随着时间（或其他变量）而变化，可以通过应用导数的概念来研究。举几个例子

• 人口增长率（无论是人类集合还是细菌群落）随时间的变化，可用于预测近期人口规模的变化。 
• 温度随位置的变化，可用于天气预报。 
• 股票市场随时间波动，可用于预测未来股市行为。 

导数也为解决优化问题提供了重要信息，我们将在接下来看到。 

导数在优化算法中的应用

我们已经看到，像梯度下降这样的优化算法，通过应用导数来寻求达到误差（或成本）函数的全局最小值。 

让我们更仔细地看看导数告诉我们关于误差函数的信息，通过进行与汽车示例相同的练习。 

为此，让我们考虑以下一维函数优化测试函数

f(x) = –x sin(x)

我们可以对f(x)应用乘积法则来找到其一阶导数，记为f’(x)，然后再次对f’(x)应用乘积法则来找到二阶导数，记为f’’(x)

f’(x) = -sin(x) – x cos(x)

f’’(x) = x sin(x) – 2 cos(x)

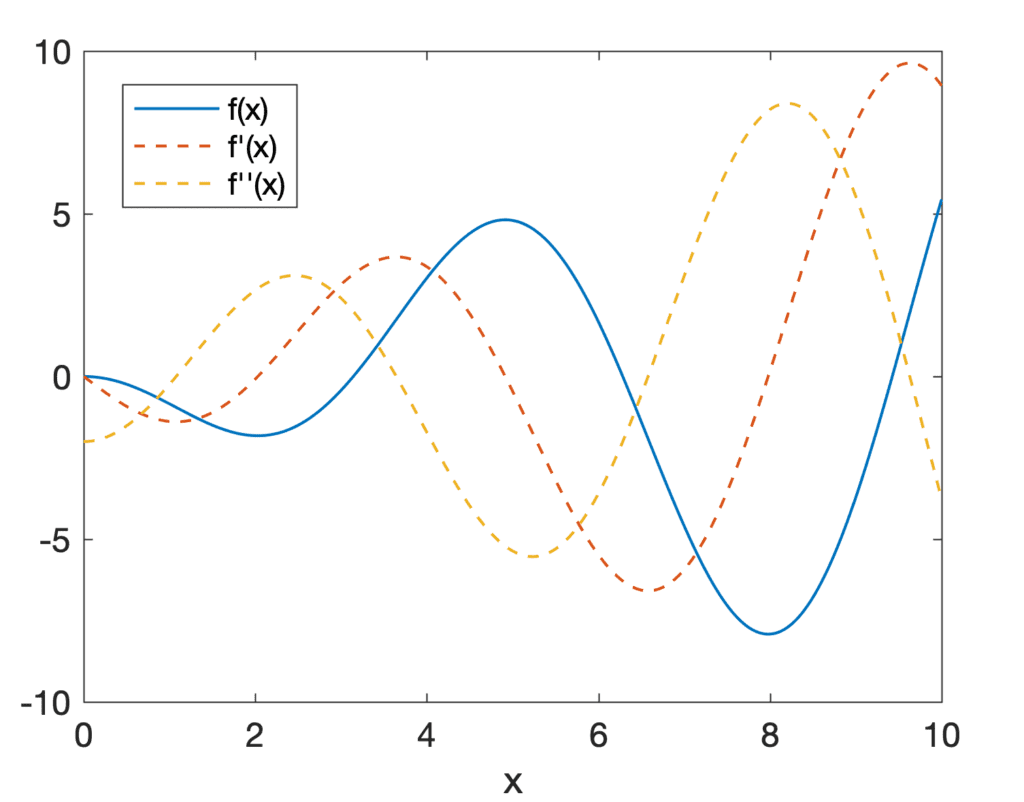
我们可以绘制这三个函数在不同x 值下的图像来可视化它们

函数f(x)、其一阶导数f'(x)和二阶导数f''(x)的线图

与我们之前在汽车示例中观察到的类似，一阶导数的图表明了f(x)的变化方式和变化量。例如，正导数表示f(x)是一个增函数，而负导数表示f(x)现在正在减小。因此，如果在寻找函数最小值时，优化算法根据其学习率 ε 对输入进行微小更改

x_new = x – ε  f’(x)

那么算法可以通过移动到与导数相反的方向（通过反转符号）来减小f(x)。 

我们也可能对求函数的二阶导数感兴趣。

我们可以将二阶导数视为衡量曲率。 

– 第86页，《深度学习》，2017年。

例如，如果算法到达一个导数为零的临界点，它仅凭f’(x)无法区分该点是局部最大值、局部最小值、鞍点还是平坦区域。然而，当二阶导数介入时，算法就可以知道该临界点是局部最小值（如果二阶导数大于零）。对于局部最大值，二阶导数小于零。因此，二阶导数可以告知优化算法应该向哪个方向移动。不幸的是，对于鞍点和平坦区域，该测试仍然 inconclusive，这两种情况的二阶导数都为零。 

基于梯度下降的优化算法不使用二阶导数，因此被称为一阶优化算法。利用二阶导数的优化算法，例如牛顿法，则称为二阶优化算法。 

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 微积分傻瓜书, 2016.
• 无限力量, 2020.
• 深度学习, 2017.
• 优化算法, 2019.

总结

在本教程中，您发现了导数的不同应用。 

具体来说，你学到了：

• 导数可以应用于我们身边遇到的现实生活问题。 
• 导数对于机器学习中的函数优化至关重要。 

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

掌握机器学习微积分！

通过微积分概念变得更聪明

...通过更好地理解微积分的符号和术语

在我的新电子书中探索如何实现
机器学习微积分

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
微分、梯度、拉格朗日乘子法、雅可比矩阵等等...

将恰到好处的微积分知识带到
您的机器学习项目

查看内容