应用机器学习具有挑战性,因为为给定问题设计一个完美的学习系统是无法实现的。
您的任务没有最好的训练数据或最好的算法,只有您能发现的最好的。
应用机器学习最好被视为一个搜索问题,目的是在给定知识和可用资源的情况下,为输入到输出的最佳映射找到解决方案。
在这篇文章中,您将了解应用机器学习作为搜索问题的概念化。
阅读本文后,你将了解:
- 应用机器学习是从输入到输出的未知底层映射函数的近似问题。
- 诸如数据选择和算法选择等设计决策缩小了您最终可能选择的可能映射函数的范围。
- 将机器学习概念化为搜索有助于解释集成方法的使用、算法的抽查以及理解算法学习时发生的情况。
通过我的新书《机器学习优化》开启您的项目,其中包括分步教程和所有示例的Python源代码文件。
让我们开始吧。
将应用机器学习作为一个搜索问题的简明介绍
图片作者:tonko43,保留部分权利。
概述
本文分为5个部分;它们是
- 函数近似问题
- 函数近似作为搜索
- 数据选择
- 算法选择
- 机器学习作为搜索的含义
函数近似问题
应用机器学习是开发学习系统以解决特定学习问题。
学习问题的特点是包含输入数据和输出数据的观测值,以及两者之间一些未知但连贯的关系。
学习系统的目标是学习输入和输出数据之间的广义映射,以便对来自输出变量未知的领域的新实例进行熟练的预测。
在统计学习中,即机器学习的统计学视角,问题被定义为在给定输入数据(X)和相关输出数据(y)的情况下学习映射函数(f)。
|
1 |
y = f(X) |
我们拥有 X 和 y 的样本,并尽力找到一个近似 f 的函数,例如 fprime,以便将来我们可以根据新的示例(Xhat)进行预测(yhat)。
|
1 |
yhat = fprime(Xhat) |
因此,应用机器学习可以被认为是函数逼近问题。
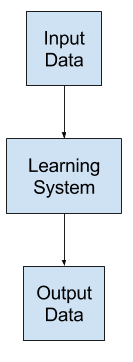
机器学习作为从输入到输出的映射
所学到的映射将是不完美的。
设计和开发学习系统的问题是学习一个对输入变量到输出变量的未知底层函数进行有用近似的问题。
我们不知道函数的具体形式,因为如果我们知道,就不需要学习系统;我们可以直接指定解决方案。
因为我们不知道真正的底层函数,所以我们必须对其进行近似,这意味着我们不知道也可能永远不知道学习系统与真实映射的近似程度。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
函数近似作为搜索
我们必须寻找一个足够好的真实底层函数的近似值,以满足我们的目的。
有许多噪声源会将误差引入学习过程,这会使过程更具挑战性,从而导致映射的实用性降低。例如:
- 学习问题框架的选择。
- 用于训练系统的观测数据的选择。
- 训练数据准备方式的选择。
- 预测模型的表示形式选择。
- 选择用于在训练数据上拟合模型的学习算法。
- 选择用于评估预测技能的性能指标。
还有更多。
您会发现,在开发学习系统时有许多决策点,而且没有一个答案是预先知道的。
您可以将所有可能的学习系统视为一个巨大的搜索空间,其中每个决策点都会缩小搜索范围。
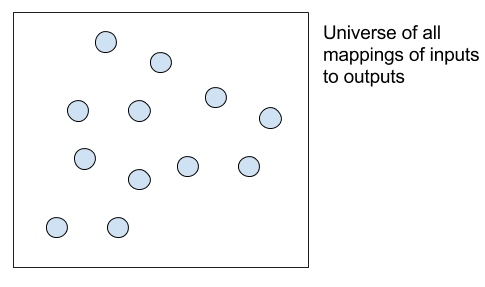
从输入到输出的所有可能映射函数的搜索空间
例如,如果学习问题是预测花卉的物种,数百万个可能的学习系统之一可以按如下方式缩小范围
- 选择将问题框定为预测物种类别标签,例如分类。
- 选择给定物种及其相关亚种的花卉测量数据。
- 选择一个特定苗圃中的花卉进行测量,以收集训练数据。
- 选择决策树模型表示,以便向利益相关者解释预测结果。
- 选择CART算法来拟合决策树模型。
- 选择分类准确率来评估模型的技能。
等等。
您还可以看到,开发学习系统所涉及的许多决策可能存在自然的层次结构,每个决策都会进一步缩小我们可能构建的学习系统的空间。
这种缩小引入了一种有用的偏差,它有意识地选择了一部分可能的学习系统,而不是另一部分,目的是更接近一个我们可以在实践中使用的有用映射。这种偏差既适用于问题框架的顶层,也适用于低层,例如机器学习算法或算法配置的选择。
数据选择
学习问题的选择性框架和用于训练系统的数据是开发学习系统的一个重要杠杆点。
您无法访问所有数据:即所有输入和输出对。如果您可以,就不需要预测模型来对新的输入观测进行输出预测。
您确实有一些历史输入-输出对。如果没有,您将没有任何数据来训练预测模型。
但也许您有很多数据,只需要选择其中的一部分进行训练。或者,您可能可以随意生成数据,但又面临着要生成或收集什么以及多少数据的问题。
您选择用于建模学习系统的数据必须充分捕捉输入和输出数据之间的关系,既要适用于您已有的数据,也要适用于模型将来需要进行预测的数据。
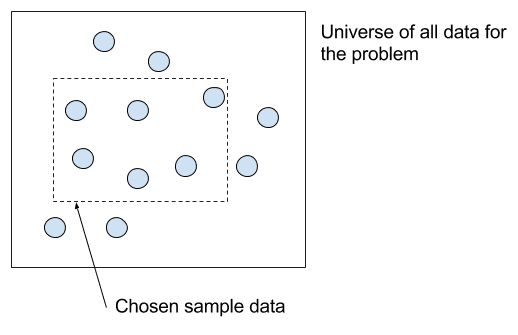
从问题的所有数据中选择训练数据
算法选择
您必须选择模型的表示形式以及用于在训练数据上拟合模型的算法。这又是开发学习系统的一个重要杠杆点。
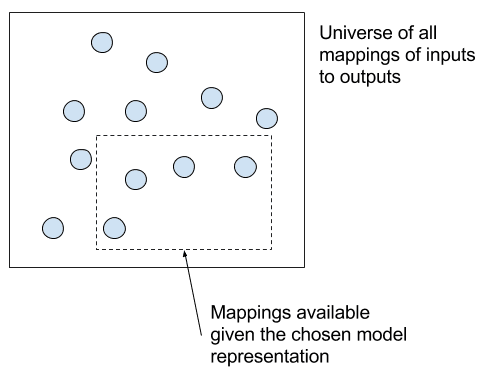
从所有算法中选择一个问题算法
通常,这个决策被简化为算法的选择,尽管项目利益相关者经常对项目施加约束,例如模型必须能够解释预测结果,这反过来又对最终模型表示的形式施加了约束,从而限制了您可以搜索的映射范围。
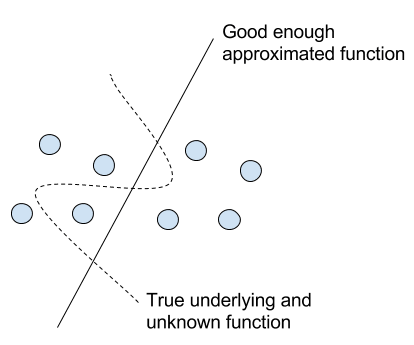
选择近似输入到输出映射的效果
机器学习作为搜索的含义
将学习系统的开发概念化为搜索问题有助于阐明应用机器学习中的许多相关问题。
本节将探讨其中几个。
迭代学习算法
用于学习映射的算法将施加进一步的约束,它与所选的算法配置一起,将控制在拟合模型时如何导航可能候选映射的空间(例如,对于迭代学习的机器学习算法)。
在这里,我们可以看到机器学习算法从训练数据中学习的行为实际上是在导航学习系统可能映射的空间,希望能从糟糕的映射转向更好的映射(例如,爬山算法)。
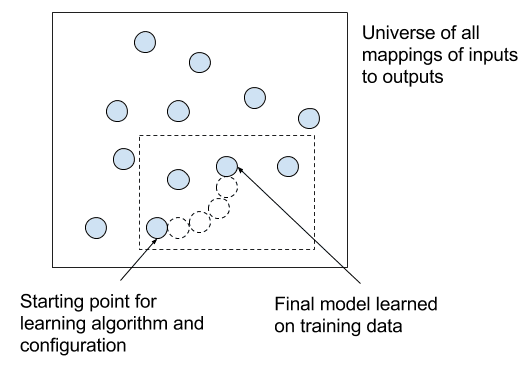
学习算法在数据上迭代训练的效果
这为机器学习算法核心中优化算法的作用提供了概念上的依据,以最大限度地利用特定训练数据的模型表示。
集成方法的原理
我们还可以看到,不同的模型表示将在所有可能的函数映射空间中占据截然不同的位置,并且在进行预测时也会表现出截然不同的行为(例如,不相关的预测误差)。
这为集成方法的作用提供了概念性依据,这些方法结合了来自不同但熟练的预测模型的预测结果。
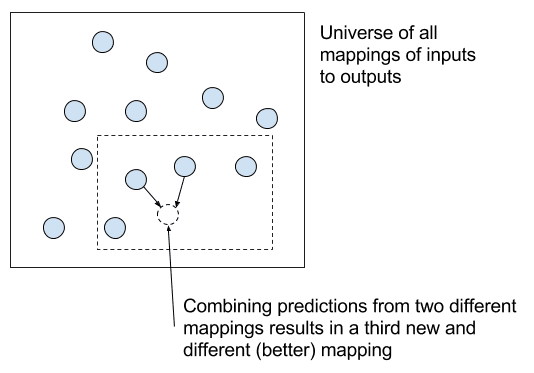
解释多个最终模型预测的组合
抽样检查的原理
具有不同表示的不同算法可能在可能的函数映射空间中从不同的位置开始,并将以不同的方式导航空间。
如果这些算法正在导航的受限空间由适当的框架和良好数据明确指定,那么大多数算法可能会发现良好且相似的映射函数。
我们还可以看到,良好的框架和对训练数据的仔细选择如何为一系列现代强大的机器学习算法开辟候选映射空间。
这为在给定机器学习问题上对一套算法进行抽样检查提供了理由,并对最有希望的算法加倍投入,或者选择最简洁的解决方案(例如,奥卡姆剃刀原理)。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
- 第2章,机器学习, 1997.
- 泛化作为搜索, 1982.
- 第 1 章,数据挖掘:实用机器学习工具和技术, 2016.
- 论算法选择及其在组合搜索问题中的应用, 2012.
- 维基百科上的算法选择
总结
在这篇文章中,您了解了应用机器学习作为搜索问题的概念化。
具体来说,你学到了:
- 应用机器学习是从输入到输出的未知底层映射函数的近似问题。
- 诸如数据选择和算法选择等设计决策缩小了您最终可能选择的可能映射函数的范围。
- 将机器学习概念化为搜索有助于解释集成方法的使用、算法的抽样检查以及理解算法学习时发生的情况。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






这篇帖子很棒!我想看到更多这样的帖子。另外,如果您能多写一些关于机器学习的统计方法,那就更好了!
谢谢!
很有趣。很有道理。
谢谢,
罗伯托·卡德纳
谢谢罗伯托。
谢谢杰森,这些简化的解释让它很容易理解和联系起来。
谢谢,很高兴听到。
Jason,
这是一篇很棒的文章,引出了一些问题,也许可以写一篇单独的博客来分享您对此的看法。我在工作中看到机器学习应用程序类型普遍发生转变,并且不同通用类别算法之间存在实际竞争,这似乎与它们如何应用于所使用的“搜索”算法类型有很大关系,正如您指出的那样。特别是,我看到曾经仅限于特定专业任务(如图像和语音处理)的神经网络,现在由于配置变化而崭露头角,通常与我们一些“经典”机器学习技术的佼佼者(例如XGBoost)竞争。在文献或研究中,您是否知道有任何系统性尝试通过密切跟踪新神经网络技术发展过程中的效率变化来跟踪这种转变,并将其与经典机器学习进行比较?结果将是,在特定情况下,我们将知道何时需要考虑改变我们用于欺诈检测等基准案例的高级分析策略……
克雷格
好问题,克雷格。
将技术映射到问题是无法实现的。例如,输入特征的微小变化就可能极大地改变“问题”。
我们能做的最好的事情是在遇到的每个具体问题上评估一系列方法,看看哪种方法效果最好。
任何关于神经网络适用于“A”而XGBoost适用于“B”的说法,归根结底可能都只是轶事。
我们通常没有足够的资源进行全面的评估,所以捷径是使用其他人(在文献中)报告有效的G方法。
这有帮助吗?
先生,它是高级语言。像我这样的人怎么能理解呢?请尝试用低级语言来解释,以便我们理解。
很抱歉听到这个消息。您不明白哪一部分?
谢谢杰森,这些富有成果的想法!
我认为机器学习/深度学习的主要成功取决于其背后的数学!数学可能是一个严重的问题(当您深入研究非常复杂的符号公式和定理时,那时真的很难跟上)。但数学也可以用“直观”或近似的方式(稍后通常可以迭代以获得更深入的方法)作为一种自然工具来解释基本或物理或类比概念,以引入您的问题或案例。
谈到您博客中的这些空间(即下面的数学),算法模型(以及输入/输出数据)“生活在”其中,我的建议是也引入希尔伯特空间(https://en.wikipedia.org/wiki/Hilbert_space)的数学思想,它具有无限维度,甚至包括无限函数的领域。
也就是说,我想每个人都有“欧几里得空间”的“自然”概念,例如角度、向量、投影、维度(通常是3D)、作为距离的度量,这些都源于这个平面上的标量和向量乘法。所以直观的力量来自于“几何方法”……那么当我们外推到超过3D的更高维度时会发生什么?函数而不是数字呢?或者无限维度而不是有限欧几里得维度呢?……这些真的很难处理(所以符号和数学公式取代了您的自然概念,并将您带入无限维度,无限投影,……即使没有人能从物理上理解它……所以我想希尔伯特空间方法在数据和机器学习/深度学习方法数学模型/算法方法中会有很多问题要处理……
对我来说,来自欧几里得方法的最自然的想法之一是度量(向量的距离)和投影(我们如何将算法或数据等分解或分割成其他更熟悉的部分……我猜过滤器和卷积层在机器学习/深度学习中就是这样做的……但因为它具有无限维度,我们只捕捉到一些模式(图像,数据,……)……像这样可视化卷积层非常有帮助(至少对我来说)。
这篇博客的另一个想法,除了希尔伯特空间“逻辑和数学方法”之外,还需要提到启发式方法,即没有理性或完整的方法来寻找最佳或最优解,但存在许多更直观的方法,使我们能够找到特定的解决方案,即使它们根本不是最优解,仍在等待被发现,如果它们存在的话(因为它们存在于一个“无限域”中)……
数学可以增加深度,但并非必需。
我不需要知道如何设计甚至修理内燃机就能开车。
好的
非常感谢,亲爱的。
确实,对应用机器学习的介绍如此温和:简洁且信息丰富!
很高兴它有帮助。
杰森,我喜欢您分享知识和见解。我妻子觉得我在假期里读这些东西很傻,但学习是如此令人愉快。我对您感激不尽。
谢谢,纳尔逊!
您也选择了一篇很棒的文章来阅读,我非常喜欢“机器学习即搜索”的思维方式。
谢谢您的文章,杰森。
我有很多您的资料。
非常感谢。
谢谢。
非常精确,绝对计划阅读每一篇博客。
谢谢 Jason。
谢谢。