使用 ROC 曲线评估和比较分类器性能

分类器性能最常报告的指标是准确率：即正确分类的百分比。

此指标的优点是易于理解，并且可以轻松地比较不同分类器的性能，但它忽略了许多在诚实评估分类器性能时应考虑的因素。

什么是分类器性能？

分类器性能不仅仅是正确分类的数量。

例如，考虑筛查宫颈癌等相对罕见疾病的问题，其患病率约为 10%（实际统计数据）。如果一个懒惰的巴氏涂片筛查员将他们看到的每个样本都归类为“正常”，那么他们的准确率将为 90%。非常令人印象深刻！但这个数字完全忽略了 10% 的患病女性根本没有被诊断出来的事实。

一些性能指标

在之前的一篇博文中，我们讨论了一些可用于评估分类器的其他性能指标。回顾一下

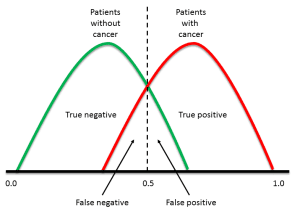
大多数分类器会产生一个分数，然后对该分数进行阈值处理以决定分类。如果分类器产生一个介于 0.0（肯定为阴性）和 1.0（肯定为阳性）之间的分数，通常认为大于 0.5 的任何值都为阳性。

但是，应用于数据集（其中 PP 是阳性人群，NP 是阴性人群）的任何阈值都将产生真阳性（TP）、假阳性（FP）、真阴性（TN）和假阴性（FN）（图 1）。我们需要一种方法来考虑所有这些数字。

图 1. 重叠的数据集将始终产生假阳性和假阴性以及真阳性和真阴性

一旦您拥有了所有这些度量的数字，就可以计算出一些有用的度量。

• 准确率 = (1 – 错误率) = (TP + TN)/(PP + NP) = Pr(C)，正确分类的概率。
• 灵敏度 = TP/(TP + FN) = TP/PP = 测试在患病人群中检测疾病的能力。
• 特异度 = TN/(TN + FP) = TN / NP = 测试在无病人群中正确排除疾病的能力。

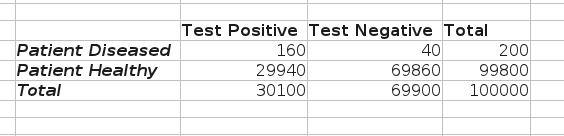
让我们为一些合理的实际数字计算这些度量。如果我们有 100,000 名患者，其中 200 名（20%）实际上患有癌症，我们可能会看到以下测试结果（表 1）

表 1. 巴氏涂片筛查“合理”值的诊断测试性能说明

对于这些数据

• 灵敏度 = TP/(TP + FN) = 160 / (160 + 40) = 80.0%
  特异度 = TN/(TN + FP) = 69,860 / (69,860 + 29,940) = 70.0%

换句话说，我们的测试将正确识别 80% 的患者，但 30% 的健康人将被错误地检测为阳性。仅考虑测试的灵敏度（或准确率），可能会丢失重要信息。

通过考虑我们错误的以及正确的答案，我们可以更深入地了解分类器的性能。

克服必须选择截止值的难题的一种方法是，从 0.0 的阈值开始，这样所有情况都被视为阳性。我们正确地分类了所有阳性病例，并错误地分类了所有阴性病例。然后，我们将阈值移动到 0.0 和 1.0 之间的每个值，逐渐减少假阳性数量并增加真阳性数量。

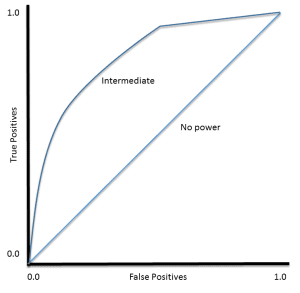
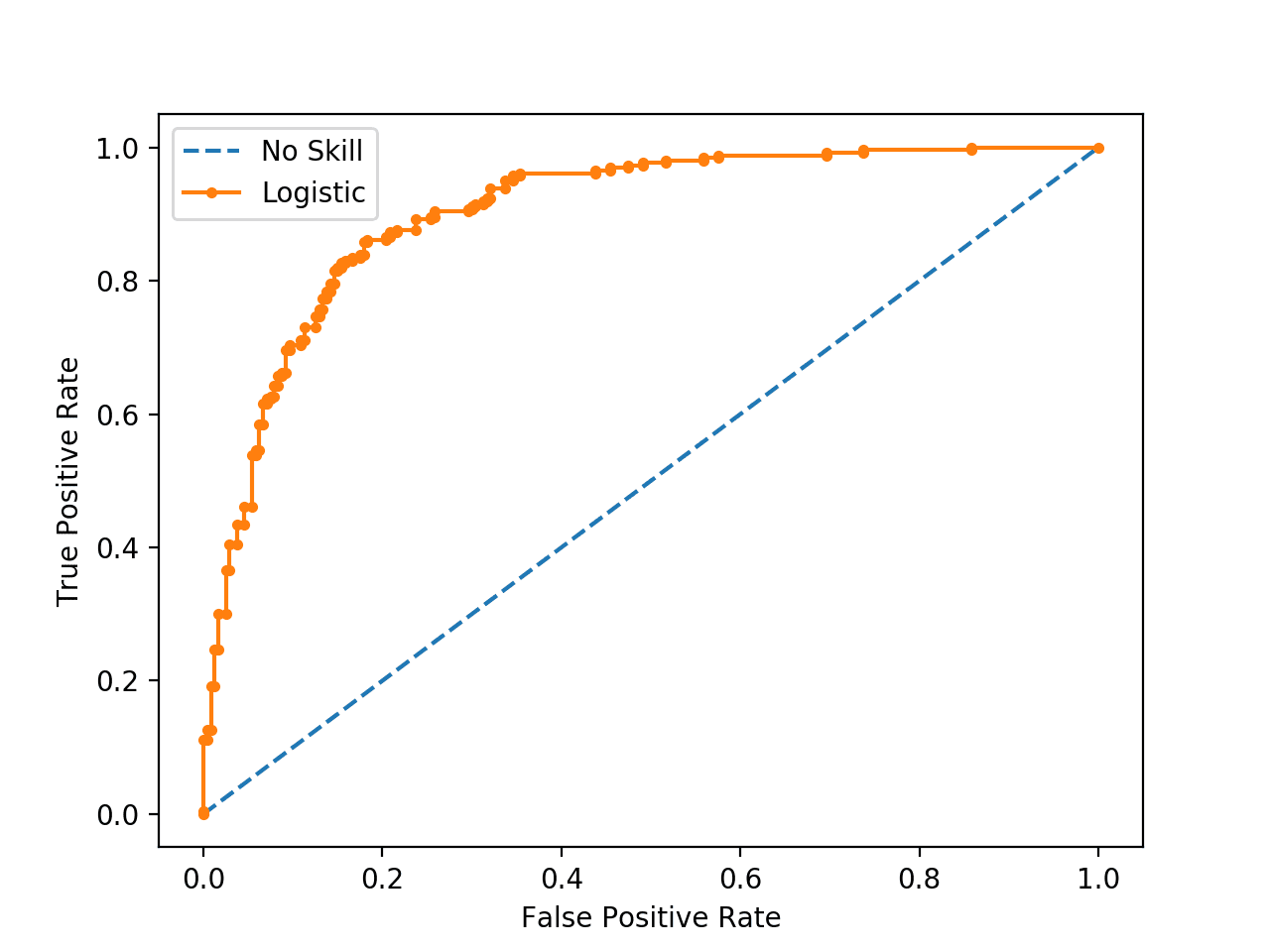
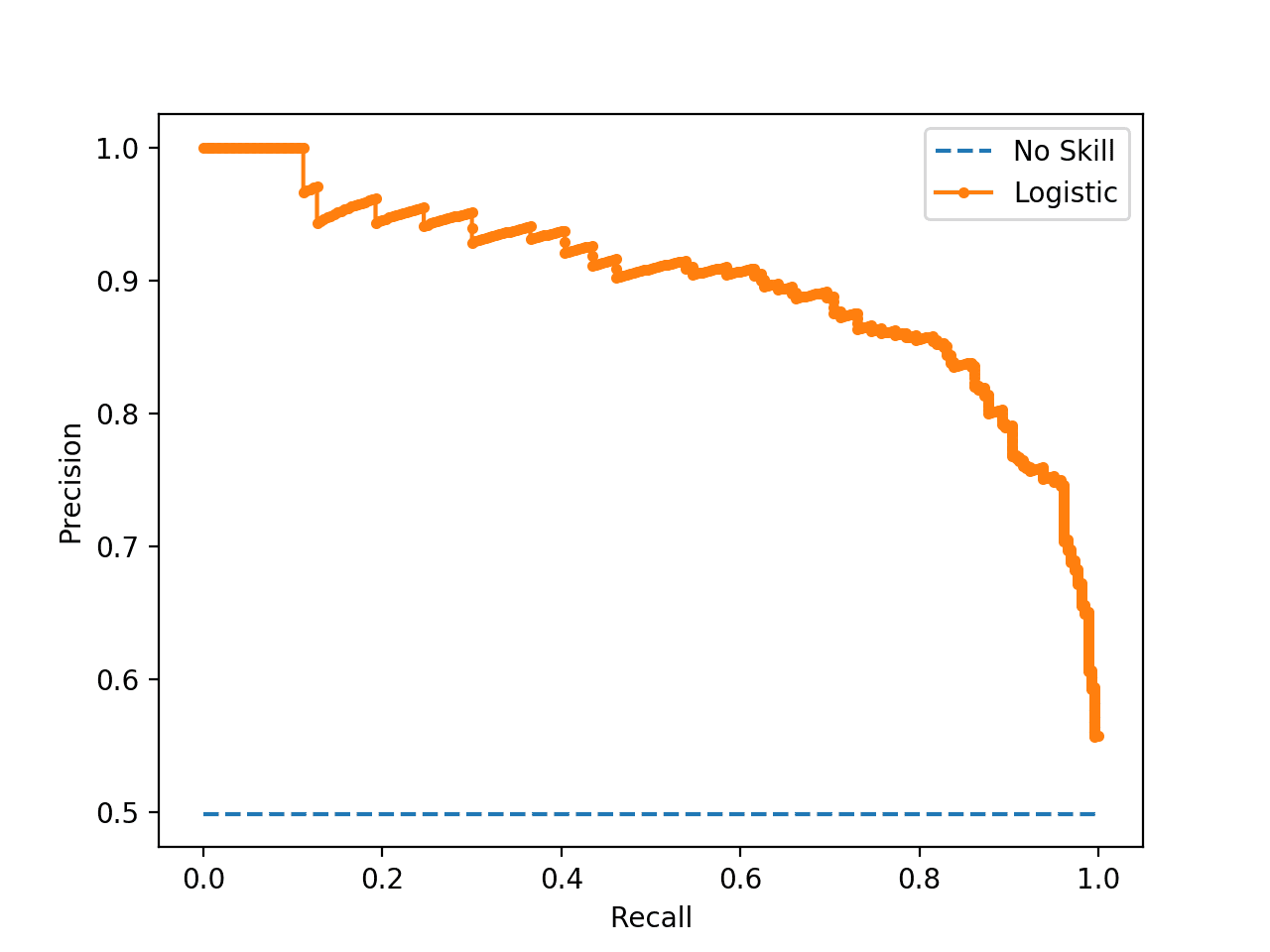
然后，可以将 TP（灵敏度）与 FP（1 – 特异度）绘制在每个使用的阈值上。生成的图称为接收者操作特征（ROC）曲线（图 2）。ROC 曲线是在 1950 年代用于雷达回波的信号检测，此后已应用于广泛的问题。

图 2. ROC 曲线示例

对于完美的分类器，ROC 曲线将直接沿着 Y 轴向上延伸，然后沿着 X 轴向右延伸。没有区分能力的分类器将位于对角线上，而大多数分类器则介于两者之间。

ROC 分析提供了独立于（并且在指定）成本背景或类别分布的工具，用于选择可能的最佳模型并丢弃次优模型

— 接收者操作特征维基百科文章

使用 ROC 曲线

阈值选择

显而易见，ROC 曲线可用于选择分类器的阈值，该阈值可最大化真阳性，同时最小化假阳性。

但是，不同类型的问题具有不同的最佳分类器阈值。例如，对于癌症筛查测试，我们可能愿意接受相对较高的假阳性率以获得高真阳性，识别可能的癌症患者是最重要的。

然而，对于治疗后的随访测试，可能需要一个不同的阈值，因为我们希望最小化假阴性，我们不希望告诉患者他们已康复（如果事实并非如此）。

性能评估

ROC 曲线还使我们能够评估分类器在其整个操作范围内的性能。最广泛使用的度量是曲线下的面积（AUC）。从图 2 可以看出，没有区分能力、基本上随机猜测的分类器的 AUC 为 0.5，因为曲线沿着对角线。那个神话般的完美分类器的 AUC 为 1.0。大多数分类器的 AUC 介于这两个值之间。

AUC 小于 0.5 可能表明发生了一些有趣的事情。非常低的 AUC 可能表明问题设置错误，分类器发现了数据中的一种关系，这种关系本质上与预期相反。在这种情况下，检查整个 ROC 曲线可能会提供一些关于正在发生什么的线索：是阳性和阴性被错误标记了吗？

分类器比较

AUC 可用于比较两个或多个分类器的性能。可以选择一个阈值来比较该点的分类器性能，或者通过考虑 AUC 来比较整体性能。

大多数已发表的报告以绝对方式比较 AUC：“分类器 1 的 AUC 为 0.85，分类器 2 的 AUC 为 0.79，因此分类器 1 明显更好”。但是，可以计算 AUC 差异是否在统计学上显著。有关详细信息，请参阅下面的 Hanley & McNeil (1982) 论文。

ROC 曲线分析教程

• 使用 SigmaPlot 软件生成 ROC 曲线的教程 (PDF)
• 来自 TheRMUoHP 生物统计学资源频道为 SPSS 制作的 YouTube 教程
• R 中 pROC 包的文档 (PDF)

何时使用 ROC 曲线分析

在这篇文章中，我使用了生物医学示例，ROC 曲线广泛用于生物医学领域。然而，该技术适用于任何产生每个案例分数而非二元决策的分类器。

神经网络和许多统计算法是合适的分类器的示例，而决策树等方法则不太适合。只有两个可能结果的算法（如这里使用的癌症/无癌症示例）最适合此方法。

任何可以输入到适当分类器中的数据都可以进行 ROC 曲线分析。

进一步阅读

• 一篇关于使用 ROC 曲线的经典论文，虽然年代久远，但仍然非常相关：Hanley, J. A. and B. J. McNeil (1982). “接收者操作特征（ROC）曲线下面积的含义和用途。” Radiology 143(1): 29-36。
• 以及一篇不错的、较新的综述文章，重点是医学诊断：Hajian-Tilaki K. “用于医学诊断测试评估的接收者操作特征（ROC）曲线分析”。Caspian Journal of Internal Medicine 2013;4(2):627-635。
• 仅用于演示 ROC 曲线在金融应用中的使用：Petro Lisowsky (2010) “寻求避税：使用财务报表信息实证建模避税天堂”。The Accounting Review: 2010 年 9 月，第 85 卷，第 5 期，第 1693-1720 页。