概率推断涉及使用概率模型来估计期望值或密度。通常,使用概率模型直接推断值是不可行的,因此必须使用近似方法。马尔可夫链蒙特卡洛采样提供了一类用于从高维概率分布中进行系统随机采样的算法。与蒙特卡洛采样方法不同,它 […]


概率推断涉及使用概率模型来估计期望值或密度。通常,使用概率模型直接推断值是不可行的,因此必须使用近似方法。马尔可夫链蒙特卡洛采样提供了一类用于从高维概率分布中进行系统随机采样的算法。与蒙特卡洛采样方法不同,它 […]

蒙特卡洛方法是一类用于随机采样概率分布的技术。在许多问题领域中,描述或估计概率分布相对容易,但计算期望的量是不可行的。这可能出于多种原因,例如领域本身的随机性或指数级的数量 […]
最大似然估计是一种通过搜索概率分布及其参数来估计数据集密度的方法。它是一种通用且有效的方法,是许多机器学习算法的基础,尽管它要求训练数据集是完整的,例如,所有相关的相互作用的随机变量都存在。当 […] 时,最大似然变得不可行。

模型选择是从一组候选模型中选择一个模型的问题。通常选择在保留测试数据集上表现最好的模型,或者使用重采样技术(如 k 折交叉验证)来估计模型性能。模型选择的另一种方法是使用概率统计度量 […]

逻辑回归是用于二元分类预测建模的模型。逻辑回归模型的参数可以通过称为最大似然估计的概率框架来估计。在此框架下,必须假定目标变量(类别标签)的概率分布,然后定义一个似然函数,该函数计算观察到 […] 的概率。

线性回归是用于预测数值量的经典模型。线性回归模型的参数可以通过最小二乘法或最大似然估计过程来估计。最大似然估计是一个概率框架,用于自动查找最佳描述观测数据的概率分布和参数。监督 […]
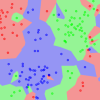
在本教程中,您将学习 K 最近邻算法,包括它的工作原理以及如何在 Python 中从头开始实现它(无需库)。一种简单但强大的预测方法是利用与新数据最相似的历史示例。这就是 K 最近邻 […] 原理。

密度估计是估计问题域观测样本的概率分布的问题。有许多用于解决密度估计的技术,尽管机器学习领域中一个常用的框架是最大似然估计。最大似然估计涉及定义一个似然函数来计算条件概率 […]

交叉熵在机器学习中通常用作损失函数。交叉熵是信息论领域的一个度量,它建立在熵的基础上,并通常计算两个概率分布之间的差异。它与 KL 散度密切相关但又不同,KL 散度计算两个概率分布之间的相对熵,而交叉熵 […]

在本教程中,您将学习朴素贝叶斯算法,包括它的工作原理以及如何在 Python 中从头开始实现它(无需库)。我们可以使用概率在机器学习中进行预测。也许最广泛使用的例子是朴素贝叶斯算法。它不仅简单[…]