作者归档 | Jason Brownlee

对于给定的随机变量，量化概率分布之间的差异通常是可取的。这在机器学习中经常发生，因为我们可能对计算实际概率分布与观测概率分布之间的差异感兴趣。这可以通过信息论中的技术来实现，例如 Kullback-Leibler 散度（KL 散度），或者 [...]

信息增益计算通过某种方式转换数据集后熵或惊奇度的减少量。它通常用于通过评估每个变量的信息增益来构建决策树，并选择最大化信息增益的变量，从而最小化熵并产生最佳 [...]

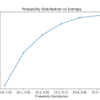
信息论是数学的一个子领域，涉及通过有噪声信道传输数据。信息论的基石是量化消息中有多少信息量的思想。更广泛地说，这可以用于量化事件和随机变量中的信息，称为熵，其计算 [...]

概率模型可以定义变量之间的关系并用于计算概率。例如，全条件模型可能需要大量数据来覆盖所有可能的情况，而且在实践中计算概率可能非常困难。诸如所有随机变量的条件独立性之类的简化假设可能很有效，例如 [...]

在本教程中，您将学习如何为复杂的优化问题实现贝叶斯优化算法。全局优化是一个具有挑战性的问题，即找到一个输入，该输入能够使给定目标函数的成本最小化或最大化。通常，目标函数的形式很复杂且难以分析，并且 [...]

分类是一个预测建模问题，涉及为给定的输入数据样本分配一个标签。分类预测建模问题可以表述为计算给定数据样本的类标签的条件概率。贝叶斯定理为计算此条件概率提供了一种原则性的方法，尽管在实践中需要 [...]

贝叶斯定理为计算条件概率提供了一种原则性的方法。它是一个看似简单的计算，尽管它可以用来轻松计算直觉经常出错的事件的条件概率。尽管它是概率领域中的一个强大工具，但贝叶斯定理也广泛用于 [...]

机器学习概率速成班。在 7 天内掌握机器学习中使用的概率。概率是一个被普遍认为是机器学习基石的数学领域。尽管概率是一个庞大的领域，有许多晦涩的理论和发现，但其基本工具和表示法 [...]

概率计算令人沮丧地违反直觉。我们的大脑过于急于走捷径而得出错误的答案，而不是仔细思考问题并正确计算概率。为了使这个问题变得明显并帮助培养直觉，通过解决应用概率中的经典问题可能会有所帮助。这些问题，例如 [...]

单个随机变量的概率很简单，但当考虑两个或多个变量时，它可能会变得复杂。对于两个变量，我们可能对两个同时发生的事件的概率感兴趣，称为联合概率：一个事件发生在另一个事件发生的情况下，称为条件概率，或者只是 [...]