自编码器是一种可以用来学习原始数据压缩表示的神经网络。
自编码器由编码器和解码器子模型组成。编码器压缩输入,解码器则尝试从编码器提供的压缩版本中重新创建输入。训练完成后,编码器模型被保存,而解码器则被丢弃。
然后,编码器可以作为一种数据准备技术,对原始数据执行特征提取,用于训练不同的机器学习模型。
在本教程中,您将学习如何开发和评估用于回归预测的自编码器
完成本教程后,您将了解:
- 自编码器是一种神经网络模型,可用于学习原始数据的压缩表示。
- 如何在一个训练数据集上训练自编码器模型,并仅保存模型的编码器部分。
- 如何在训练机器学习模型时将编码器用作数据准备步骤。
让我们开始吧。

用于回归的自编码器特征提取
图片由Simon Matzinger拍摄,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 自编码器用于特征提取
- 用于回归的自编码器
- 自编码器作为数据准备
自编码器用于特征提取
一个 自动编码器 是一个旨在学习输入数据压缩表示的神经网络模型。
自编码器是一种训练后试图将其输入复制到其输出的神经网络。
——第502页,深度学习,2016年。
它们是一种无监督学习方法,尽管从技术上讲,它们是使用监督学习方法(称为自监督学习)进行训练的。它们通常作为更广泛模型的一部分进行训练,该模型尝试重新创建输入。
例如
- X = 模型.预测(X)
自动编码器模型的设计通过在模型中间设置瓶颈(bottleneck)来有意地增加这一难度,然后从瓶颈处进行输入数据的重构。
自动编码器有很多类型,其用途各不相同,但最常见的用途可能是作为学习到的或自动化的特征提取模型。
在这种情况下,一旦模型拟合,模型的重建部分可以被丢弃,并且可以使用直到瓶颈点的模型。模型在瓶颈处的输出是一个固定长度的向量,它提供了输入数据的压缩表示。
通常,它们受到限制,只允许它们近似复制,并且只复制与训练数据相似的输入。由于模型被迫优先选择输入中的哪些方面应该被复制,它通常能学习到数据的有用属性。
——第502页,深度学习,2016年。
然后可以将来自领域的数据输入模型,瓶颈处的模型输出可用作监督学习模型的特征向量,用于可视化,或更普遍地用于降维。
接下来,让我们探讨如何为回归预测建模问题开发用于特征提取的自编码器。
用于回归的自编码器
在本节中,我们将开发一个自编码器,以学习回归预测建模问题输入特征的压缩表示。
首先,让我们定义一个回归预测建模问题。
我们将使用 make_regression() scikit-learn 函数来定义一个合成回归任务,其中包含100个输入特征(列)和1,000个示例(行)。重要的是,我们将以一种方式定义问题,即大多数输入变量是冗余的(100个中的90个,即90%),以便自编码器稍后可以学习有用的压缩表示。
下面的示例定义了数据集并总结了其形状。
|
1 2 3 4 5 6 |
# 合成回归数据集 from sklearn.datasets import make_regression # 定义数据集 X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1) # 汇总数据集 打印(X.形状, y.形状) |
运行示例定义了数据集并打印了数组的形状,确认了行和列的数量。
|
1 |
(1000, 100) (1000,) |
接下来,我们将开发一个多层感知机(MLP)自编码器模型。
模型将接收所有输入列,然后输出相同的值。它将学习精确地重新创建输入模式。
自编码器由两部分组成:编码器和解码器。编码器学习如何解释输入并将其压缩为由瓶颈层定义的内部表示。解码器接收编码器的输出(瓶颈层)并尝试重新创建输入。
自编码器训练完成后,解码器将被丢弃,我们只保留编码器,并用它将输入示例压缩为瓶颈层输出的向量。
在这个第一个自编码器中,我们完全不压缩输入,并将使用与输入大小相同的瓶颈层。这应该是一个模型可以几乎完美学习的简单问题,旨在确认我们的模型实现正确。
我们将使用函数式 API 定义模型。如果您对此不熟悉,我推荐这个教程
在定义和拟合模型之前,我们将把数据分成训练集和测试集,并通过将值归一化到0-1的范围来缩放输入数据,这是MLP的良好实践。
|
1 2 3 4 5 6 7 8 |
... # 拆分为训练测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) # 缩放数据 t = MinMaxScaler() t.拟合(X_train) X_train = t.转换(X_train) X_test = t.转换(X_test) |
我们将把编码器定义为一个隐藏层,该隐藏层的节点数量与输入数据中的节点数量相同,并带有批归一化和 ReLU 激活函数。
接着是一个瓶颈层,其节点数量与输入数据中的列数相同,即没有压缩。
|
1 2 3 4 5 6 7 8 9 |
... # 定义编码器 可见 = 输入(形状=(n_inputs,)) e = 密集(n_inputs*2)(可见) e = 批归一化()(e) e = ReLU()(e) # 定义瓶颈层 n_bottleneck = n_inputs 瓶颈 = 密集(n_bottleneck)(e) |
解码器将以相同的结构定义。
它将有一个带有批归一化和ReLU激活的隐藏层。输出层将具有与输入数据中列数相同的节点数,并将使用线性激活函数输出数值。
|
1 2 3 4 5 6 7 8 9 10 11 |
... # 定义解码器 d = Dense(n_inputs*2)(bottleneck) d = BatchNormalization()(d) d = ReLU()(d) # 输出层 输出 = Dense(n_inputs, 激活='线性')(d) # 定义自编码器模型 模型 = 模型(输入=可见, 输出=输出) # 编译自编码器模型 模型.编译(优化器='adam', 损失='mse') |
该模型将使用高效的Adam版本随机梯度下降进行拟合,并最小化均方误差,因为重建是一种多输出回归问题。
|
1 2 3 |
... # 编译自编码器模型 模型.编译(优化器='adam', 损失='mse') |
我们可以绘制自编码器模型中的层,以了解数据如何流经模型。
|
1 2 3 |
... # 绘制自编码器 plot_model(model, 'autoencoder.png', show_shapes=True) |
下图显示了自编码器的绘制图。

用于回归的自编码器模型图
接下来,我们可以训练模型以重现输入并跟踪模型在保留测试集上的性能。该模型训练了400个epoch,批大小为16个示例。
|
1 2 3 |
... # 拟合自编码器模型以重建输入 历史 = 模型.拟合(X_train, X_train, epochs=400, batch_size=16, verbose=2, validation_data=(X_test,X_test)) |
训练完成后,我们可以绘制训练集和测试集的学习曲线,以确认模型很好地学习了重建问题。
|
1 2 3 4 5 6 |
... # 绘制损失 pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
最后,如果需要,我们可以将编码器模型保存以备后用。
|
1 2 3 4 5 6 |
... # 定义一个编码器模型(不带解码器) 编码器 = 模型(输入=可见, 输出=瓶颈) plot_model(编码器, 'encoder.png', show_shapes=True) # 将编码器保存到文件 编码器.保存('encoder.h5') |
作为保存编码器的一部分,我们还将绘制模型,以了解瓶颈层输出的形状,例如一个包含100个元素的向量。
下面提供了此图的示例。

无压缩回归编码器模型图
综上所述,下面列出了用于回归数据集重建输入数据的自编码器的完整示例,其中瓶颈层没有进行任何压缩。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# 训练用于回归的自编码器,瓶颈层不进行压缩 from sklearn.datasets import make_regression 从 sklearn.预处理 导入 MinMaxScaler from sklearn.model_selection import train_test_split 来自 tensorflow.keras.models 导入 Model 来自 tensorflow.keras.layers 导入 Input 来自 tensorflow.keras.layers 导入 Dense 来自 tensorflow.keras.layers 导入 ReLU 来自 tensorflow.keras.layers 导入 BatchNormalization 来自 tensorflow.keras.utils 导入 plot_model from matplotlib import pyplot # 定义数据集 X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1) # 输入列数 n_inputs = X.形状[1] # 拆分为训练测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) # 缩放数据 t = MinMaxScaler() t.拟合(X_train) X_train = t.转换(X_train) X_test = t.转换(X_test) # 定义编码器 可见 = 输入(形状=(n_inputs,)) e = 密集(n_inputs*2)(可见) e = 批归一化()(e) e = ReLU()(e) # 定义瓶颈层 n_bottleneck = n_inputs 瓶颈 = 密集(n_bottleneck)(e) # 定义解码器 d = Dense(n_inputs*2)(bottleneck) d = BatchNormalization()(d) d = ReLU()(d) # 输出层 输出 = Dense(n_inputs, 激活='线性')(d) # 定义自编码器模型 模型 = 模型(输入=可见, 输出=输出) # 编译自编码器模型 模型.编译(优化器='adam', 损失='mse') # 绘制自编码器 plot_model(model, 'autoencoder.png', show_shapes=True) # 拟合自编码器模型以重建输入 历史 = 模型.拟合(X_train, X_train, epochs=400, batch_size=16, verbose=2, validation_data=(X_test,X_test)) # 绘制损失 pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() # 定义一个编码器模型(不带解码器) 编码器 = 模型(输入=可见, 输出=瓶颈) plot_model(编码器, 'encoder.png', show_shapes=True) # 将编码器保存到文件 编码器.保存('encoder.h5') |
运行示例拟合模型并报告训练集和测试集上的损失。
注意:如果您在创建模型图时遇到问题,可以注释掉导入并调用 plot_model() 函数。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们看到损失变得很低但没有达到零(正如我们可能预期的那样),在瓶颈层中没有压缩。也许需要进一步调整模型架构或学习超参数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
... 第393/400轮 42/42 - 0s - 损失: 0.0025 - 验证损失: 0.0024 第394/400轮 42/42 - 0s - 损失: 0.0025 - 验证损失: 0.0021 第 395/400 轮 42/42 - 0s - 损失: 0.0023 - 验证损失: 0.0021 Epoch 396/400 42/42 - 0s - 损失: 0.0025 - 验证损失: 0.0023 Epoch 397/400 42/42 - 0s - 损失: 0.0024 - 验证损失: 0.0022 Epoch 398/400 42/42 - 0s - 损失: 0.0025 - 验证损失: 0.0021 Epoch 399/400 42/42 - 0s - 损失: 0.0026 - 验证损失: 0.0022 Epoch 400/400 42/42 - 0s - 损失: 0.0025 - 验证损失: 0.0024 |
绘制的学习曲线显示,模型在重建输入方面取得了良好的拟合,并且在整个训练过程中保持稳定,没有过拟合。
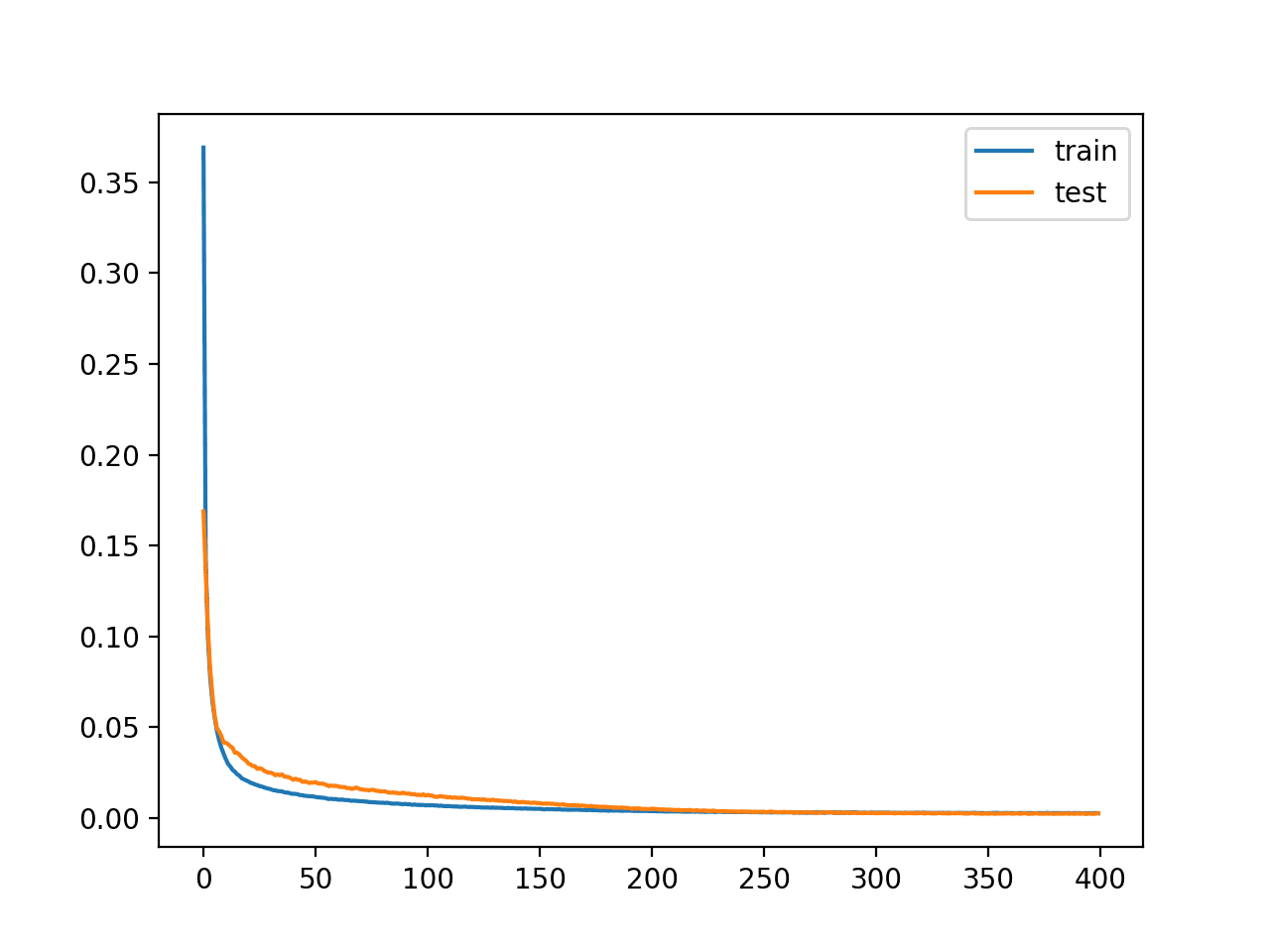
无压缩回归自编码器模型的学习曲线
到目前为止,一切顺利。我们知道如何开发一个无压缩的自编码器。
训练好的编码器保存到文件“encoder.h5”,我们可以稍后加载和使用。
接下来,让我们探讨如何使用训练好的编码器模型。
自编码器作为数据准备
在本节中,我们将使用自编码器模型中训练好的编码器模型来压缩输入数据并训练一个不同的预测模型。
首先,让我们建立该问题上的性能基线。这很重要,因为如果压缩编码没有改进模型的性能,那么压缩编码对项目就没有增加价值,不应该使用。
我们可以在训练数据集上直接训练支持向量回归(SVR)模型,并评估模型在保留测试集上的性能。
按照良好的实践,在拟合和评估模型之前,我们将对输入变量和目标变量进行缩放。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
# 使用支持向量回归模型作为性能基线 from sklearn.datasets import make_regression 从 sklearn.预处理 导入 MinMaxScaler from sklearn.model_selection import train_test_split 来自 sklearn.svm 导入 SVR 来自 sklearn.metrics 导入 mean_absolute_error # 定义数据集 X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1) # 拆分为训练测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) # 重新调整目标变量,以便我们可以对其进行转换 y_train = y_train.重塑((len(y_train), 1)) y_test = y_test.重塑((len(y_test), 1)) # 缩放输入数据 trans_in = MinMaxScaler() trans_in.拟合(X_train) X_train = trans_in.转换(X_train) X_test = trans_in.转换(X_test) # 缩放输出数据 trans_out = MinMaxScaler() trans_out.拟合(y_train) y_train = trans_out.转换(y_train) y_test = trans_out.转换(y_test) # 定义模型 模型 = SVR() # 在训练数据集上拟合模型 模型.拟合(X_train, y_train) # 在测试集上进行预测 yhat = 模型.预测(X_test) # 反转变换,以便我们可以计算误差 yhat = yhat.重塑((len(yhat), 1)) yhat = trans_out.反向转换(yhat) y_test = trans_out.反向转换(y_test) # 计算误差 得分 = mean_absolute_error(y_test, yhat) print(score) |
运行示例拟合训练数据集上的 SVR 模型并在测试集上进行评估。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到模型实现了大约89的平均绝对误差(MAE)。
我们希望并且预期,对输入进行编码后拟合的 SVR 模型能够实现更低的误差,以便将编码视为有用。
|
1 |
89.51082036130629 |
我们可以更新示例,首先使用上一节中训练的编码器模型对数据进行编码。
首先,我们可以从文件中加载训练好的编码器模型。
|
1 2 3 |
... # 从文件加载模型 编码器 = load_model('encoder.h5') |
然后,我们可以使用编码器将原始输入数据(例如100列)转换为瓶颈向量(例如100个元素向量)。
此过程可应用于训练和测试数据集。
|
1 2 3 4 5 |
... # 编码训练数据 X_train_encode = encoder.预测(X_train) # 编码测试数据 X_test_encode = encoder.预测(X_test) |
然后,我们可以像以前一样使用这些编码数据来训练和评估SVR模型。
|
1 2 3 4 5 6 7 |
... # 定义模型 模型 = SVR() # 在训练数据集上拟合模型 模型.拟合(X_train_encode, y_train) # 在测试集上进行预测 yhat = 模型.预测(X_test_encode) |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
# 使用编码输入的支持向量回归性能 from sklearn.datasets import make_regression 从 sklearn.预处理 导入 MinMaxScaler from sklearn.model_selection import train_test_split 来自 sklearn.svm 导入 SVR from sklearn.metrics import mean_absolute_error 来自 tensorflow.keras.models 导入 load_model # 定义数据集 X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1) # 拆分为训练测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) # 重新调整目标变量,以便我们可以对其进行转换 y_train = y_train.重塑((len(y_train), 1)) y_test = y_test.重塑((len(y_test), 1)) # 缩放输入数据 trans_in = MinMaxScaler() trans_in.拟合(X_train) X_train = trans_in.转换(X_train) X_test = trans_in.转换(X_test) # 缩放输出数据 trans_out = MinMaxScaler() trans_out.拟合(y_train) y_train = trans_out.转换(y_train) y_test = trans_out.转换(y_test) # 从文件加载模型 编码器 = load_model('encoder.h5') # 编码训练数据 X_train_encode = encoder.预测(X_train) # 编码测试数据 X_test_encode = encoder.预测(X_test) # 定义模型 模型 = SVR() # 在训练数据集上拟合模型 模型.拟合(X_train_encode, y_train) # 在测试集上进行预测 yhat = 模型.预测(X_test_encode) # 反转变换,以便我们可以计算误差 yhat = yhat.重塑((len(yhat), 1)) yhat = trans_out.反向转换(yhat) y_test = trans_out.反向转换(y_test) # 计算误差 得分 = mean_absolute_error(y_test, yhat) print(score) |
运行示例首先使用编码器对数据集进行编码,然后在训练数据集上拟合 SVR 模型并在测试集上进行评估。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到模型实现了大约69的平均绝对误差(MAE)。
这比在原始数据集上评估的同一模型具有更好的MAE,表明编码对于我们选择的模型和测试工具是有帮助的。
|
1 |
69.45890939600503 |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
书籍
- 深度学习, 2016.
API
文章
总结
在本教程中,您学习了如何开发和评估用于回归预测建模的自编码器。
具体来说,你学到了:
- 自编码器是一种神经网络模型,可用于学习原始数据的压缩表示。
- 如何在一个训练数据集上训练自编码器模型,并仅保存模型的编码器部分。
- 如何在训练机器学习模型时将编码器用作数据准备步骤。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



嗨,Jason,我有两个问题
1. 鉴于我们将压缩大小设置为100(无压缩),理论上我们应该实现零重建误差。为什么不是这种情况?
3. 考虑到我们没有进行压缩,我们是如何实现更小的MAE的?
为了提取显著特征,我们应该将压缩大小(瓶颈大小)设置为小于100的数字,对吗?
祝好,
加布里埃莱
一些想法:这个问题可能对于该模型来说太难完美学习,需要对架构和学习超参数进行更多调整等。
更好的表示会带来更好的学习,这与我们对原始数据使用数据转换(例如缩放或幂转换)的原因相同。
谢谢杰森!也谢谢你的博文。
不客气。
感谢您的本教程。我相信在将编码器保存到 encoder.h5 文件之前,您需要先编译它。
如果您愿意,可以这样做,它不会影响性能,因为我们不会对其进行训练——并且 compile() 只与训练模型相关。
如果你不编译它,我会收到警告,并且结果会非常不同。
您可以安全地忽略该警告。
谢谢 Jason,
这个教程来得正是时候。
如果我有两组不同的输入。第一组的形状是 n*m,第二组的形状是 n*1。
我想将这两组都用作输入。
您能给我一个提示,如何使用这两组数据构建模型,其中第一组使用自编码器进行编码?
更清楚地说:自编码器的输入形状与预测模型的输入形状不同。
是的,这个例子中,自编码器和预测模型使用了不同形状的输入
https://machinelearning.org.cn/autoencoder-for-classification/
也许您可以为每个模型使用单独的输入,这可能会有所帮助
https://machinelearning.org.cn/keras-functional-api-deep-learning/
嗨,Jason,
我注意到,在您本教程中使用的像 sklearn.datasets.make_regression 这样的人工回归数据集上,学习曲线通常没有显示任何过拟合的迹象。
例如,最近我对来自同一 sklearn.datasets 的 make_friedman 数据集生成器组的神经网络训练进行了一些实验,无论我怎么做,都无法强制我的网络在其上过拟合。
您知道这里出了什么问题吗?
也许在数据集中使用更少的噪声。
嗨,Jason,
感谢您的教程,它为开放式教育世界的“机器学习民主化”做出了巨大贡献!
正如我在您的分类模拟自编码器教程中所做的那样,我对您的基线代码进行了几次变体,以便通过自编码器统计敏感性与不同的回归模型、不同程度的特征压缩和 KFold(不同的模型训练/测试组)进行实验,因此
– 我对5个模型(线性回归、SVR、随机森林回归、极限随机树回归、XGB回归)进行了比较分析。
– 我对不同程度的压缩(无 - 未经自编码的原始输入-,1,1/2)进行了比较分析。
– 我对不同的训练/测试数据集组(带重复的 KFold)进行了统计分析。
因此我使用了 Sklearn 的“cross_val_score”函数,并且为了在其内部应用 MAE 评分,我使用了 Sklearn 的“make_score”包装器。
我的结论
– 类似于您在等效的分类教程中提供的内容。结果对所选的学习模型比应用(或不应用)自编码器更敏感。
– 在我的情况下,我使用线性回归模型获得了最佳结果(非常优化),但我也发现使用 SVR 模型应用自编码器比不使用要好。但在其他模型中,有时不应用自编码器效果更好。
– 我还更改了您的自编码器模型,并应用了分类中使用的相同模型,其中您有某种两个编码器/解码器块……结果比使用您本教程中的简单编码器/解码器稍差。
总之,正如您所说,所有这些技术都是启发式的,所以我们必须尝试许多工具并测量结果。
谢谢你,杰森!
谢谢您的好意。
非常令人印象深刻的实验!
是的,我发现回归比分类示例更具挑战性。很可能是因为选择了合成数据集。线性回归可以最优地解决合成数据集,当使用这个数据集时我尽量避免它。
我尝试运行相同的代码,但出现了此错误。请告诉我我犯了什么错误。
FailedPreconditionError:无法找到变量 dense_30/kernel。这可能意味着该变量已被删除。在 TF1 中,它也可能意味着变量未初始化。调试信息:container=localhost,status=Not found: Resource localhost/dense_30/kernel/class tensorflow::Var does not exist。
[[{{node dense_30/MatMul/ReadVariableOp}}]]
我不能说。也许你需要简化你的代码并调试以查看这个错误是如何发生的。
你好,
这是一个非常有用的教程!但是,主要是由于我缺乏编码经验,我有一些疑问,如果您能帮助我,我将不胜感激!
1) 在这个例子中,您将一个数据集分成两部分:训练集 (0.67) 和测试集 (0.33),对吗?但是,当我已经将训练集和测试集预先定义到两个不同的数据文件(例如,“train.csv”和“test.csv”)中时,我该如何处理呢?
2) 训练文件和测试文件都由 26 列组成(训练集=20631行,测试集=13096行),其中
C1 = 发动机编号(100个不同的发动机)
C2 = 时间,以周期计(目标)
C3 到 C5 = 操作设置(对所有100个发动机保持不变)
C6 到 C26 = 传感器测量值 – 21 列
我应该保留所有列吗?或者我可以排除 C1 和 C3 到 C5 吗?因为 C1 没有提供信息,而 C3 到 C5 在所有观察中都是常数。
3) 设置参数的正确方法是什么:n_samples = (“train.csv”的行数 + “test.csv”的行数?); n_features = (21?);n_informative = (会是什么?)
对于这么多的问题,我深表歉意,但我感觉这里是我唯一能找到有用且清晰的该领域信息的地方!
非常感谢您考虑我的请求。
你首先要弄清楚你研究的目标。
你想根据 C6 到 C26 预测 C2 吗?那么这就是你所需要的一切。毕竟,一个常数能否影响你的预测?
更具体地说,假设你正在对 C2 列进行回归:
1) 你可以使用提供给你的训练集和测试集,或者你可以将它们合并并打乱以创建一个主数据库,然后从那里使用 Jason 的代码(顺便说一下,这个代码也进行打乱)。
如果你指的是“如何在实践中操作”,即如何使用给你的数据……好吧,一种快速的方法是使用 pandas.read_csv 加载数据,然后将它们转换为 numpy。一个文件将是你的 X_train,另一个将是 X_test。当然,你需要将 C2 列放入相关的 y_train 和 y_test 中。查看 pandas.read_csv 文档,了解如何快速高效地完成此操作(提示:你可以选择要读取的列)。
2) 已在上面回答。
3) 这些参数只指 sklearn.datasets.make_regression。
这是一个用于创建人工数据的功能。
您将不会使用它,因此您不需要设置 n_informative(实际上,您的分析目的应该_正是_找出哪些特征是信息丰富的!)。
如果您好奇的话,等效的说法是 n_samples 是您的 X 的形状(np.shape(X)[0]),无论您决定使用什么(提供给您的数据,或者合并和重新采样的数据)。但再说一遍,您不需要它。
感谢您的良好培训。
我有一个问题。隐藏层的大小和瓶颈的大小不应该小于输入层的大小(小于100)吗?
你好 barad……以下讨论可能对你有所帮助。
https://www.researchgate.net/post/How-to-configure-the-size-of-hidden-nodes-code-in-an-autoencoder
我如何获得解码器?
嗨,罗杰里奥……以下资源可能对您有用
https://machinelearning.org.cn/implementing-the-transformer-decoder-from-scratch-in-tensorflow-and-keras/
非常感谢您在免费学习方面的慷慨。我有一个问题。您曾一次在自编码器内部改变数据比例并使用 MinMax(),然后将输出用于 SVR,然后又在 SVR 模型内部再次使用 MinMAX()?
两次缩放对结果没有显著影响吗?
你好 vahid…没有问题。
感谢您提供这个有用的教程。我最近刚开始学习和实践自编码器,所以我希望我的问题不会太基础。如果选择使用压缩,将瓶颈层设计成比输入层维度更小,是否有必要也导出解码器?或者回归模型可以直接应用于潜在空间中的表示?
谢谢!
你好 gallog-hash……您理解得非常正确,回归模型可以直接应用于潜在空间中的表示。让我们知道您用您的模型构建了什么!