使用 Python 进行时间序列预测的自回归模型

作者 Jason Brownlee 发布于 2021 年 9 月 7 日在时间序列 221

自回归是一种时间序列模型，它使用先前时间步的观测值作为回归方程的输入，以预测下一个时间步的值。

这是一个非常简单的想法，可以在一系列时间序列问题上产生准确的预测。

在本教程中，您将学习如何使用 Python 实现自回归模型进行时间序列预测。

完成本教程后，您将了解：

如何探索时间序列数据的自相关性。
如何开发自相关模型并使用它进行预测。
如何使用已开发的自相关模型进行滚动预测。

通过我的新书《使用 Python 进行时间序列预测》启动您的项目，其中包括分步教程和所有示例的Python 源代码文件。

让我们开始吧。

2017 年 5 月更新：修复了自回归方程中的一个小错字。
2019 年 4 月更新：更新了数据集链接。
2019年8月更新：更新了数据加载以使用新的API。
2019 年 9 月更新：更新了示例以使用最新的绘图 API。
2020 年 4 月更新：由于 API 更改，将 AR 更改为 AutoReg。

Autoregression Models for Time Series Forecasting With Python

使用 Python 进行时间序列预测的自回归模型
照片由 Umberto Salvagnin 提供，保留部分权利。

自回归

回归模型，例如线性回归，根据输入值的线性组合对输出值进行建模。

例如

yhat = b0 + b1*X1

1	yhat = b0 + b1*X1

其中 yhat 是预测值，b0 和 b1 是通过在训练数据上优化模型找到的系数，X 是输入值。

这种技术可以用于时间序列，其中输入变量被视为先前时间步长的观测值，称为滞后变量。

例如，我们可以根据过去两个时间步长（t-1 和 t-2）的观测值来预测下一个时间步长（t+1）的值。作为回归模型，这看起来如下：

X(t+1) = b0 + b1*X(t-1) + b2*X(t-2)

1	X(t+1) = b0 + b1X(t-1) + b2X(t-2)

由于回归模型使用来自同一输入变量在先前时间步长的数据，因此它被称为自回归（对自身的回归）。

停止以慢速学习时间序列预测！

参加我的免费7天电子邮件课程，了解如何入门（附带示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

自相关

自回归模型假设先前时间步的观测值对于预测下一个时间步的值很有用。

变量之间的这种关系称为相关性。

如果两个变量都朝同一方向变化（例如，一起上升或一起下降），则称为正相关。如果变量随着值的变化朝相反方向移动（例如，一个上升而另一个下降），则称为负相关。

我们可以使用统计量来计算输出变量与不同滞后时间步长处的先前值之间的相关性。输出变量与特定滞后变量之间的相关性越强，自回归模型在建模时可以赋予该变量的权重就越大。

同样，由于相关性是在变量本身与先前时间步长之间计算的，因此称为自相关。由于时间序列数据的序列结构，它也称为序列相关。

相关统计量还可以帮助选择哪些滞后变量在模型中会有用，哪些不会。

有趣的是，如果所有滞后变量与输出变量的相关性都很低或没有相关性，那么这表明时间序列问题可能无法预测。这在开始处理新数据集时非常有用。

在本教程中，我们将研究单变量时间序列的自相关性，然后开发一个自回归模型并使用它进行预测。

在此之前，我们首先回顾一下示例中将使用的最低日气温数据。

日最低气温数据集

此数据集描述了墨尔本市 10 年（1981-1990 年）的每日最低气温。

单位是摄氏度，共有3650个观测值。数据来源归功于澳大利亚气象局。

下载数据集.

将数据集下载到当前工作目录，文件名为“daily-min-temperatures.csv”。

以下代码将数据集加载为 Pandas Series。

from pandas import read_csv
from matplotlib import pyplot
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)
print(series.head())
series.plot()
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)

print(series.head())

series.plot()

pyplot.show()

运行示例会打印加载数据集的前 5 行。

Date
1981-01-01 20.7
1981-01-02 17.9
1981-01-03 18.8
1981-01-04 14.6
1981-01-05 15.8
Name: Temp, dtype: float64

日期

1981-01-01 20.7

1981-01-02 17.9

1981-01-03 18.8

1981-01-04 14.6

1981-01-05 15.8

名称：温度，数据类型：float64

然后创建数据集的线图。

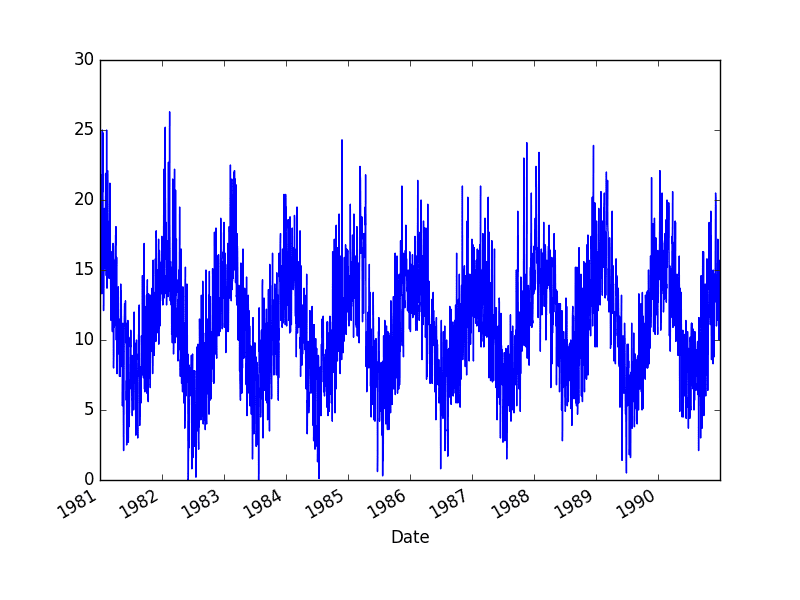
最低日气温数据集图

快速检查自相关性

我们可以进行一个快速的视觉检查，以查看时间序列数据集中是否存在自相关性。

我们可以将前一个时间步 (t-1) 的观测值与下一个时间步 (t+1) 的观测值绘制成散点图。

这可以通过手动创建时间序列数据集的滞后版本并在 Pandas 库中使用内置的散点图函数来完成。

但有一种更简单的方法。

Pandas 提供了一个内置的绘图函数来完成这项工作，称为 lag_plot() 函数。

下面是一个创建最低日气温数据集滞后图的示例。

from pandas import read_csv
from matplotlib import pyplot
from pandas.plotting import lag_plot
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)
lag_plot(series)
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

from pandas.plotting import lag_plot

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)

lag_plot(series)

pyplot.show()

运行示例将温度数据 (t) 绘制在 x 轴上，并将前一天的温度 (t-1) 绘制在 y 轴上。

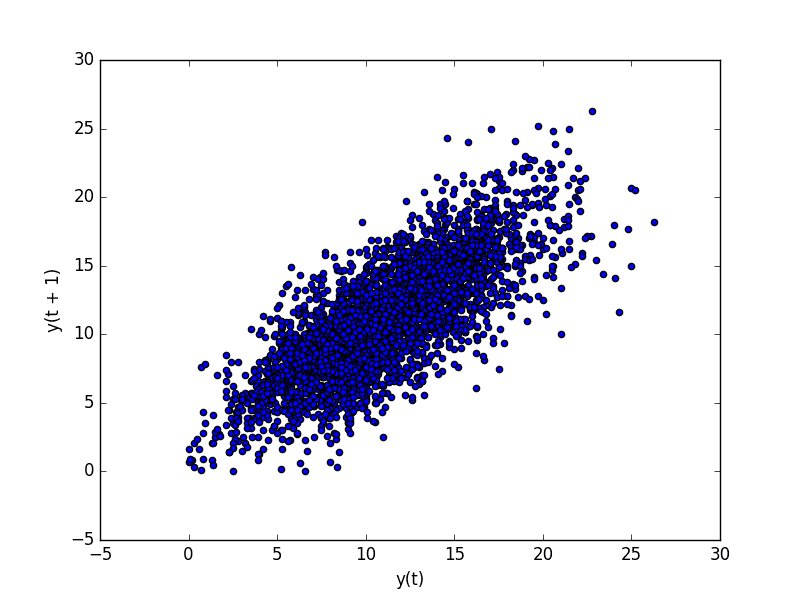
Minimum Daily Temperature Dataset Lag Plot

最低日气温数据集滞后图

我们可以看到沿着图的对角线有大量观测值。它清楚地显示了某种关系或相关性。

此过程可以对任何其他滞后观测值重复，例如如果我们想查看与过去 7 天或上个月或去年同天的关系。

我们还可以进行的另一个快速检查是直接计算观测值和滞后变量之间的相关性。

我们可以使用统计检验，例如 Pearson 积矩相关系数。这会生成一个数字来总结两个变量之间的相关程度，范围在 -1（负相关）和 +1（正相关）之间，接近零的小值表示低相关，高于 0.5 或低于 -0.5 的高值表示高相关。

可以使用滞后数据集的 DataFrame 上的 corr() 函数轻松计算相关性。

下面的示例创建了最低日气温数据集的滞后版本，并计算了每列与其他列（包括自身）的相关矩阵。

from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
result = dataframe.corr()
print(result)

from pandas import read_csv

from pandas import DataFrame

从 pandas 导入 concat

from matplotlib import pyplot

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)

values = DataFrame(series.values)

dataframe = concat([values.shift(1), values], axis=1)

dataframe.columns = ['t-1', 't+1']

result = dataframe.corr()

print(result)

这很好地证实了上面的图。

它显示了观测值与滞后 1 值之间存在强烈的正相关（0.77）。

         t-1      t+1
t-1  1.00000  0.77487
t+1  0.77487  1.00000

t-1 t+1

t-1 1.00000 0.77487

t+1 0.77487 1.00000

这对于一次性检查很有用，但如果我们想检查时间序列中的大量滞后变量，就会很繁琐。

接下来，我们将探讨这种方法的放大版本。

自相关图

我们可以绘制每个滞后变量的相关系数。

这可以非常快速地了解哪些滞后变量可能是预测模型中使用的良好候选变量，以及观测值与其历史值之间的关系如何随时间变化。

我们可以手动计算每个滞后变量的相关值并绘制结果。幸运的是，Pandas 提供了一个内置的绘图函数，称为 autocorrelation_plot() 函数。

该图的 x 轴表示滞后数，y 轴表示 -1 到 1 之间的相关系数。该图还包括实线和虚线，分别表示相关值的 95% 和 99% 置信区间。高于这些线的相关值比低于这些线的更显著，为选择更相关的滞后值提供了阈值或截止点。

from pandas import read_csv
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)
autocorrelation_plot(series)
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

from pandas.plotting import autocorrelation_plot

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)

autocorrelation_plot(series)

pyplot.show()

运行示例显示了随着前一年夏季和冬季气温值的变化，正相关和负相关的波动。

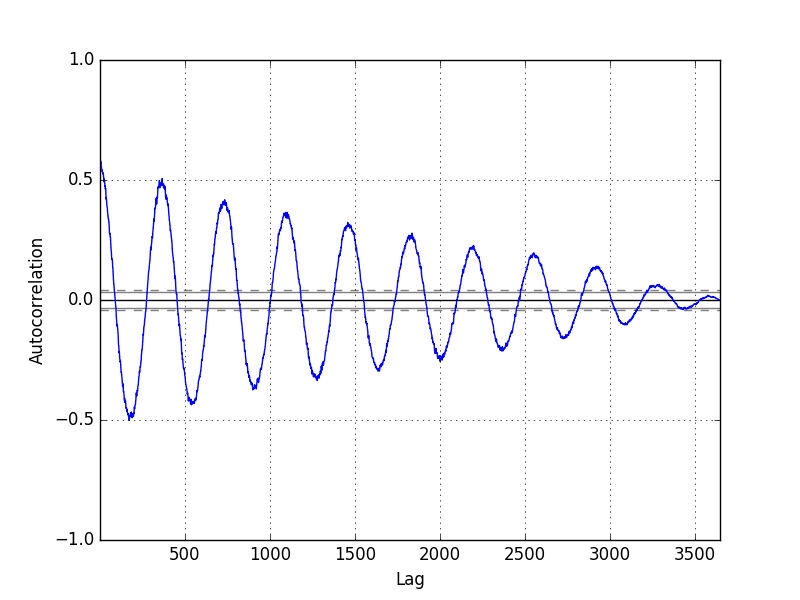
Pandas 自相关图

statsmodels 库还在 plot_acf() 函数中以线图的形式提供了该图的一个版本。

from pandas import read_csv
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)
plot_acf(series, lags=31)
pyplot.show()

from pandas import read_csv

from matplotlib import pyplot

from statsmodels.graphics.tsaplots import plot_acf

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)

plot_acf(series, lags=31)

pyplot.show()

在此示例中，我们为了可读性将评估的滞后变量限制为 31。

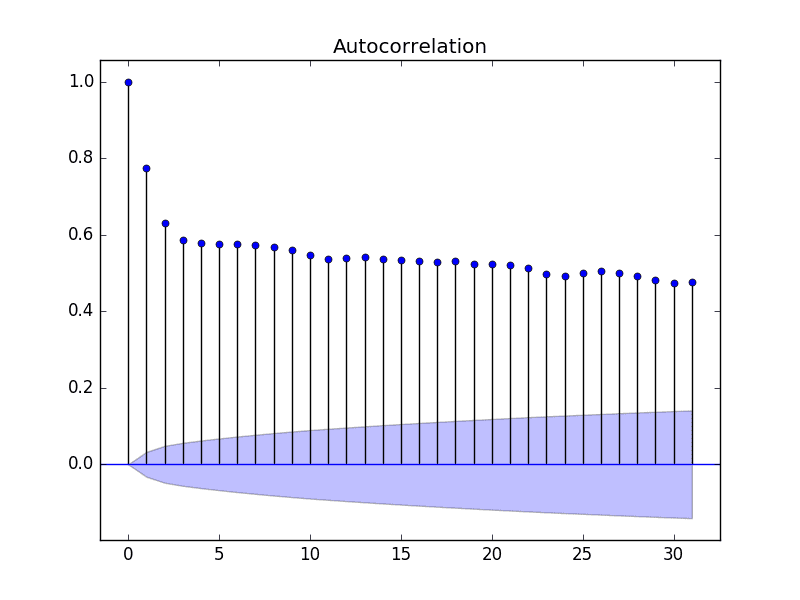
Statsmodels 自相关图

现在我们知道了如何查看时间序列中的自相关性，接下来让我们看看如何使用自回归进行建模。

在此之前，我们先确定一个基线性能。

持久性模型

假设我们想要开发一个模型，根据所有先前的观测值来预测数据集中最后 7 天的最低温度。

我们可以用来进行预测的最简单的模型是保持最后一次观测值。我们可以称之为持久性模型，它为我们提供了一个问题性能的基线，我们可以将其与自回归模型进行比较。

我们可以通过将观测值分成训练集和测试集来开发问题的测试工具，其中数据集中最后 7 个观测值被分配到测试集作为我们希望预测的“未见”数据。

预测是使用步进验证模型进行的，这样我们就可以保留最近的观测值用于第二天。这意味着我们不是进行 7 天预测，而是进行 7 次 1 天预测。

from pandas import read_csv
from pandas import DataFrame
from pandas import concat
from matplotlib import pyplot
from sklearn.metrics import mean_squared_error
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)
# create lagged dataset
values = DataFrame(series.values)
dataframe = concat([values.shift(1), values], axis=1)
dataframe.columns = ['t-1', 't+1']
# split into train and test sets
X = dataframe.values
train, test = X[1:len(X)-7], X[len(X)-7:]
train_X, train_y = train[:,0], train[:,1]
test_X, test_y = test[:,0], test[:,1]

# persistence model
def model_persistence(x):
	return x

# walk-forward validation
predictions = list()
for x in test_X:
	yhat = model_persistence(x)
	predictions.append(yhat)
test_score = mean_squared_error(test_y, predictions)
print('Test MSE: %.3f' % test_score)
# plot predictions vs expected
pyplot.plot(test_y)
pyplot.plot(predictions, color='red')
pyplot.show()

from pandas import read_csv

from pandas import DataFrame

从 pandas 导入 concat

from matplotlib import pyplot

from sklearn.metrics import mean_squared_error

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0)

# 创建滞后数据集

values = DataFrame(series.values)

dataframe = concat([values.shift(1), values], axis=1)

dataframe.columns = ['t-1', 't+1']

# 拆分为训练集和测试集

X = dataframe.values

train, test = X[1:len(X)-7], X[len(X)-7:]

train_X, train_y = train[:,0], train[:,1]

test_X, test_y = test[:,0], test[:,1]

# 持久性模型

def model_persistence(x):

返回 x

# 步进验证

predictions = list()

for x in test_X:

yhat = model_persistence(x)

predictions.append(yhat)

test_score = mean_squared_error(test_y, predictions)

print('Test MSE: %.3f' % test_score)

# 绘制预测值与期望值

pyplot.plot(test_y)

pyplot.plot(predictions, color='red')

pyplot.show()

运行示例将打印均方误差 (MSE)。

该值提供了问题的基线性能。

Test MSE: 3.423

1	测试 MSE: 3.423

绘制了接下来 7 天的预期值（蓝色）与模型的预测值（红色）。

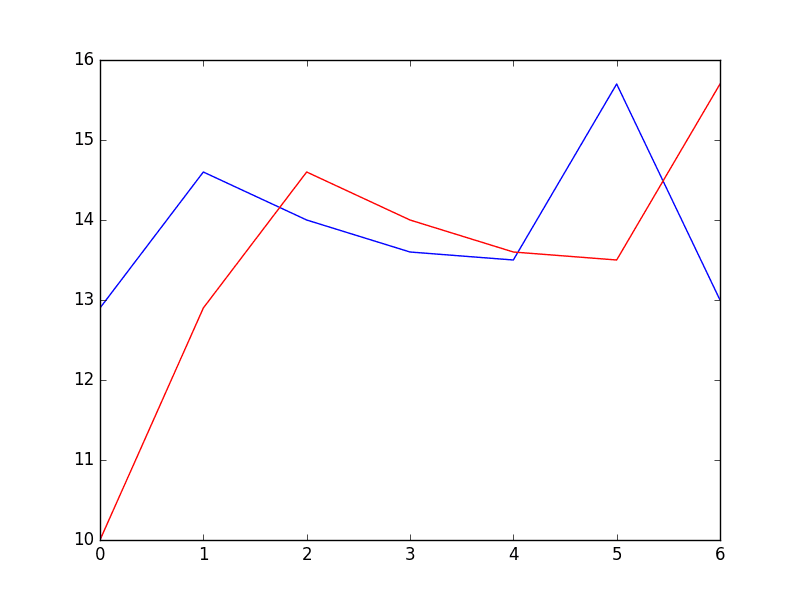
持久性模型的预测

自回归模型

自回归模型是一种线性回归模型，它使用滞后变量作为输入变量。

我们可以使用 scikit-learn 中的 LinearRegession 类手动计算线性回归模型，并手动指定要使用的滞后输入变量。

另外，statsmodels 库提供了一个自回归模型，您必须指定一个适当的滞后值并训练一个线性回归模型。它在 AutoReg 类中提供。

我们可以通过首先创建 AutoReg() 模型，然后调用 fit() 在我们的数据集上训练它来使用该模型。这会返回一个 AutoRegResults 对象。

一旦拟合完成，我们可以通过调用 predict() 函数对未来的一些观测值进行预测。这会创建一个 1 个 7 天的预测，这与上面的持久性示例不同。

完整的示例如下所示。

# create and evaluate a static autoregressive model
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.tsa.ar_model import AutoReg
from sklearn.metrics import mean_squared_error
from math import sqrt
# load dataset
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0, parse_dates=True, squeeze=True)
# split dataset
X = series.values
train, test = X[1:len(X)-7], X[len(X)-7:]
# train autoregression
model = AutoReg(train, lags=29)
model_fit = model.fit()
print('Coefficients: %s' % model_fit.params)
# make predictions
predictions = model_fit.predict(start=len(train), end=len(train)+len(test)-1, dynamic=False)
for i in range(len(predictions)):
	print('predicted=%f, expected=%f' % (predictions[i], test[i]))
rmse = sqrt(mean_squared_error(test, predictions))
print('Test RMSE: %.3f' % rmse)
# plot results
pyplot.plot(test)
pyplot.plot(predictions, color='red')
pyplot.show()

# 创建并评估静态自回归模型

from pandas import read_csv

from matplotlib import pyplot

from statsmodels.tsa.ar_model import AutoReg

from sklearn.metrics import mean_squared_error

from math import sqrt

# 加载数据集

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0, parse_dates=True, squeeze=True)

# 分割数据集

X = series.values

train, test = X[1:len(X)-7], X[len(X)-7:]

# 训练自回归模型

model = AutoReg(train, lags=29)

model_fit = model.fit()

print('Coefficients: %s' % model_fit.params)

# 进行预测

predictions = model_fit.predict(start=len(train), end=len(train)+len(test)-1, dynamic=False)

for i in range(len(predictions)):

print('predicted=%f, expected=%f' % (predictions[i], test[i]))

rmse = sqrt(mean_squared_error(test, predictions))

print('Test RMSE: %.3f' % rmse)

# 绘制结果

pyplot.plot(test)

pyplot.plot(predictions, color='red')

pyplot.show()

运行示例后，将打印训练好的线性回归模型中的系数列表。

然后打印 7 天预测结果，并总结预测的均方误差。

Coefficients: [ 5.57543506e-01  5.88595221e-01 -9.08257090e-02  4.82615092e-02
  4.00650265e-02  3.93020055e-02  2.59463738e-02  4.46675960e-02
  1.27681498e-02  3.74362239e-02 -8.11700276e-04  4.79081949e-03
  1.84731397e-02  2.68908418e-02  5.75906178e-04  2.48096415e-02
  7.40316579e-03  9.91622149e-03  3.41599123e-02 -9.11961877e-03
  2.42127561e-02  1.87870751e-02  1.21841870e-02 -1.85534575e-02
 -1.77162867e-03  1.67319894e-02  1.97615668e-02  9.83245087e-03
  6.22710723e-03 -1.37732255e-03]
predicted=11.871275, expected=12.900000
predicted=13.053794, expected=14.600000
predicted=13.532591, expected=14.000000
predicted=13.243126, expected=13.600000
predicted=13.091438, expected=13.500000
predicted=13.146989, expected=15.700000
predicted=13.176153, expected=13.000000
Test RMSE: 1.225

系数：[ 5.57543506e-01 5.88595221e-01 -9.08257090e-02 4.82615092e-02

4.00650265e-02 3.93020055e-02 2.59463738e-02 4.46675960e-02

1.27681498e-02 3.74362239e-02 -8.11700276e-04 4.79081949e-03

1.84731397e-02 2.68908418e-02 5.75906178e-04 2.48096415e-02

7.40316579e-03 9.91622149e-03 3.41599123e-02 -9.11961877e-03

2.42127561e-02 1.87870751e-02 1.21841870e-02 -1.85534575e-02

-1.77162867e-03 1.67319894e-02 1.97615668e-02 9.83245087e-03

6.22710723e-03 -1.37732255e-03]

预测值=11.871275, 期望值=12.900000

预测值=13.053794, 期望值=14.600000

预测值=13.532591, 期望值=14.000000

预测值=13.243126, 期望值=13.600000

预测值=13.091438, 期望值=13.500000

预测值=13.146989, 期望值=15.700000

预测值=13.176153, 期望值=13.000000

测试 RMSE：1.225

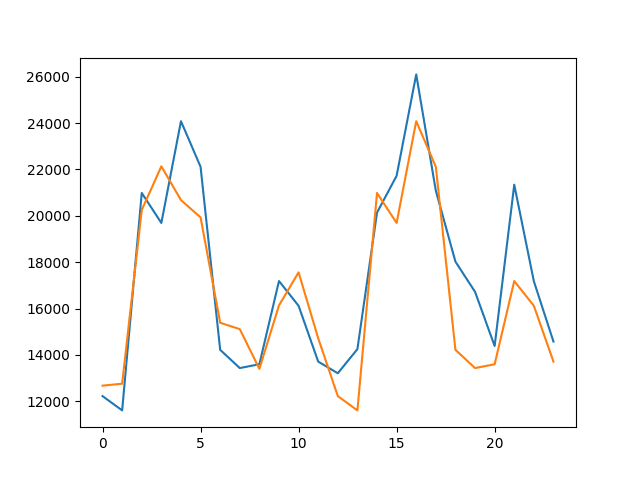
绘制了预期值（蓝色）与预测值（红色）的图。

预测看起来相当不错（每天大约相差 1 摄氏度），但在第 5 天有较大的偏差。

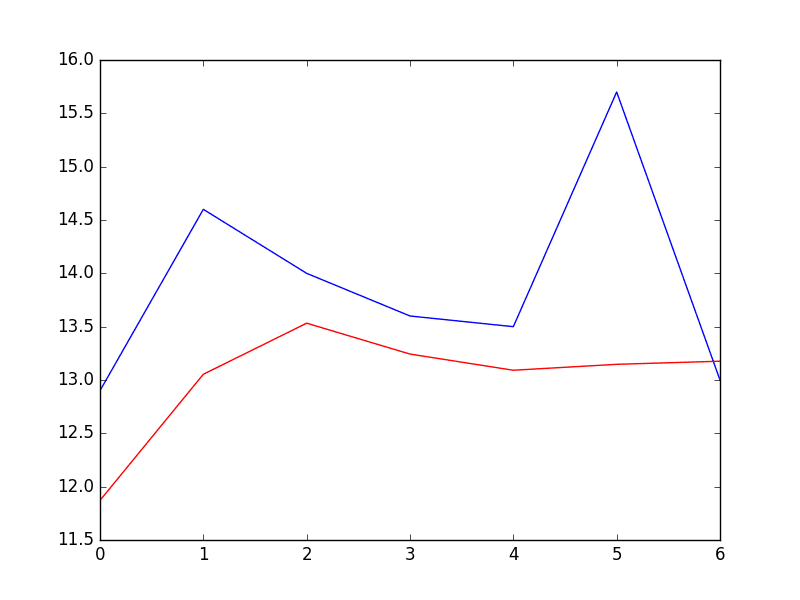
固定 AR 模型的预测

statsmodels API 不支持在新观测值可用时轻松更新模型。

一种方法是每天在新观测值可用时重新训练 AutoReg 模型，这可能是一种有效的方法，尽管计算成本较高。

另一种方法是使用学习到的系数手动进行预测。这需要保留 29 个先前观测值的历史记录，并从模型中检索系数并将其用于回归方程以得出新的预测。

系数以数组形式提供，其中包含截距项，然后是每个滞后变量的系数，从 t-1 到 t-n。我们只需按照正确的顺序在观测值历史记录上使用它们，如下所示：

yhat = b0 + b1*X1 + b2*X2 ... bn*Xn

1	yhat = b0 + b1X1 + b2X2 ... bn*Xn

下面是完整的示例。

# create and evaluate an updated autoregressive model
from pandas import read_csv
from matplotlib import pyplot
from statsmodels.tsa.ar_model import AutoReg
from sklearn.metrics import mean_squared_error
from math import sqrt
# load dataset
series = read_csv('daily-min-temperatures.csv', header=0, index_col=0, parse_dates=True, squeeze=True)
# split dataset
X = series.values
train, test = X[1:len(X)-7], X[len(X)-7:]
# train autoregression
window = 29
model = AutoReg(train, lags=29)
model_fit = model.fit()
coef = model_fit.params
# walk forward over time steps in test
history = train[len(train)-window:]
history = [history[i] for i in range(len(history))]
predictions = list()
for t in range(len(test)):
	length = len(history)
	lag = [history[i] for i in range(length-window,length)]
	yhat = coef[0]
	for d in range(window):
		yhat += coef[d+1] * lag[window-d-1]
	obs = test[t]
	predictions.append(yhat)
	history.append(obs)
	print('predicted=%f, expected=%f' % (yhat, obs))
rmse = sqrt(mean_squared_error(test, predictions))
print('Test RMSE: %.3f' % rmse)
# plot
pyplot.plot(test)
pyplot.plot(predictions, color='red')
pyplot.show()

# 创建并评估更新的自回归模型

from pandas import read_csv

from matplotlib import pyplot

from statsmodels.tsa.ar_model import AutoReg

from sklearn.metrics import mean_squared_error

from math import sqrt

# 加载数据集

series = read_csv('daily-min-temperatures.csv', header=0, index_col=0, parse_dates=True, squeeze=True)

# 分割数据集

X = series.values

train, test = X[1:len(X)-7], X[len(X)-7:]

# 训练自回归模型

window = 29

model = AutoReg(train, lags=29)

model_fit = model.fit()

coef = model_fit.params

# 遍历测试集中的时间步

history = train[len(train)-window:]

history = [history[i] for i in range(len(history))]

predictions = list()

for t in range(len(test)):

length = len(history)

lag = [history[i] for i in range(length-window,length)]

yhat = coef[0]

for d in range(window):

yhat += coef[d+1] * lag[window-d-1]

obs = test[t]

predictions.append(yhat)

history.append(obs)

print('predicted=%f, expected=%f' % (yhat, obs))

rmse = sqrt(mean_squared_error(test, predictions))

print('Test RMSE: %.3f' % rmse)

# 绘图

pyplot.plot(test)

pyplot.plot(predictions, color='red')

pyplot.show()

同样，运行示例会打印预测值和均方误差。

predicted=11.871275, expected=12.900000
predicted=13.659297, expected=14.600000
predicted=14.349246, expected=14.000000
predicted=13.427454, expected=13.600000
predicted=13.374877, expected=13.500000
predicted=13.479991, expected=15.700000
predicted=14.765146, expected=13.000000
Test RMSE: 1.204

预测值=11.871275, 期望值=12.900000

预测值=13.659297, 期望值=14.600000

预测值=14.349246, 期望值=14.000000

预测值=13.427454, 期望值=13.600000

预测值=13.374877, 期望值=13.500000

预测值=13.479991, 期望值=15.700000

预测值=14.765146, 期望值=13.000000

测试 RMSE: 1.204

我们可以看到在比较误差分数时，预测结果略有改进。

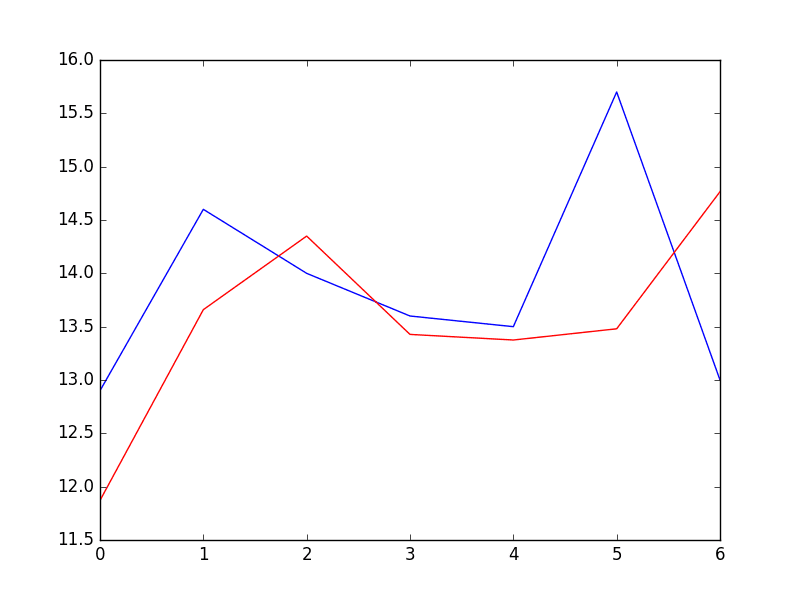
滚动 AR 模型的预测

进一步阅读

本节提供了一些资源，如果您想更深入地了解自相关和自回归。

自相关维基百科
自回归模型维基百科
第 7 章 – 基于回归的模型：自相关和外部信息，《R 语言实用时间序列预测：一本实践指南》。
第 4.5 节 – 自回归模型，《R 语言时间序列入门》。

总结

在本教程中，您学习了如何使用 Python 对时间序列数据进行自回归预测。

具体来说，你学到了：

关于自相关和自回归以及它们如何用于更好地理解时间序列数据。
如何使用图表和统计检验探索时间序列中的自相关性。
如何使用 Python 训练自回归模型并将其用于短期和滚动预测。

您对自回归或本教程有什么疑问吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何使用 Python 检查时间序列数据是否平稳

使用 Python 进行时间序列数据可视化

221 条评论：使用 Python 进行时间序列预测的自回归模型

Gary Bake 2017 年 1 月 5 日下午 11:35 #

感谢杰森的精彩文章

万一有人遇到我遇到的同样问题 –
我从上面的链接下载了 csv 文件中的数据。
由于温度列中有三行包含“？”，导致导入失败。
一旦这些被删除，数据就可以正常导入。

回复
- Jason Brownlee 2017 年 1 月 6 日上午 9:10 #
  
  谢谢提醒，加里。
  
  回复
  - yaser alsultan 2019年12月16日下午3:57 #
    
    你好，伙计，你认为处理小时数据的最佳模型是什么？
    
    回复
    - Jason Brownlee 2019年12月17日上午6:29 #
      
      没有最好的算法。我建议测试一套方法，以发现哪种方法最适合您的特定数据集。
      
      回复
Tim Melino 2017年1月14日上午10:28 #

嘿，Jason，谢谢你的文章。当预期值未知时，您将如何从文件末尾进行预测？

回复
- Jason Brownlee 2017年1月15日上午5:27 #
  
  Tim，您可以使用model.predict()，如示例中所示，并指定要预测的时间步长的索引。
  
  回复
  - Siddhant Bhambri 2018年10月16日上午12:47 #
    
    嘿，Jason，我对model.predict()的使用不太清楚。如果模型已经学习了今天之前的值，您能帮我预测未来10天的值吗？
    
    回复
    - Jason Brownlee 2018年10月16日上午6:39 #
      
      当然，请看这篇帖子
      https://machinelearning.org.cn/make-sample-forecasts-arima-python/
      
      回复
Farrukh Jalali 2017年1月25日下午4:16 #

嗨，Jason，

感谢您所有精彩的博客。它们确实帮助了很多。关于这篇文章的一个问题是，我认为AR建模也假定时间序列是平稳的，因为观测值应该是独立同分布的。statsmodels库中的AR函数是否检查平稳性，并根据需要自行使用去趋势去季节化时间序列？另外，如果我们使用sckit learn库进行AR模型，如您所述，我们是否需要自行检查并进行调整？

回复
- Jason Brownlee 2017年1月26日上午4:45 #
  
  你好，Farrukh，好问题。
  
  statsmodels中的AR确实假定数据是平稳的。
  
  如果您的数据不平稳，您必须使其平稳（例如，差分和其他变换）。
  
  回复
  - Farrukh Jalali 2017年1月31日下午12:19 #
    
    谢谢你的回答。虽然我们在上面的例子中没有对趋势/季节平稳性进行适当的测试，但从图中看，似乎存在季节效应。那么在这种情况下，应用AR模型是否可行？
    
    回复
    - Jason Brownlee 2017年2月1日上午10:39 #
      
      好问题，Farrukh。
      
      AR旨在用于平稳数据，即没有季节性或趋势信息的数据。
      
      回复
Farrukh Jalali 2017年1月31日下午11:07 #

或者更具体地说，是否可以直接将AR模型应用于给定数据，而不检查季节性并在存在季节性时将其移除（这在第一个图中显示出一些迹象）？

回复
- Muneeb 2020年11月11日上午4:19 #
  
  你好。我正在做类似的事情，我也有同样的问题？在上面的AR模型中，使用了正常的未转换时间序列，并且没有使其平稳？这是正确和适用的吗？
  
  回复
  - Jason Brownlee 2020年11月11日上午6:53 #
    
    在使用AR模型之前，最好使序列平稳。
    
    回复

Anthony of Sydney 2017年3月8日上午5:09 #

尊敬的Jason博士，
我尝试了“持久性模型”部分。
我使用的数据集是sp500.csv数据集。
根据您的代码

# persistence model
def model_persistence(x):
	return x
 
# walk-forward validation
predictions = list()
for x in test_X:
	yhat = model_persistence(x)
	predictions.append(yhat)
test_score = mean_squared_error(test_y, predictions)

# 持久性模型

def model_persistence(x):

返回 x

# 步进验证

predictions = list()

for x in test_X:

yhat = model_persistence(x)

predictions.append(yhat)

test_score = mean_squared_error(test_y, predictions)

我一尝试计算“test_score”，就收到以下错误，

Traceback (most recent call last):
  File "", line 1, in 
    test_score = mean_squared_error(test_y,predictions)
  File "C:\Python34\lib\site-packages\sklearn\metrics\regression.py", line 232, in mean_squared_error
    output_errors = np.average((y_true - y_pred) ** 2, axis=0,
TypeError: ufunc 'subtract' did not contain a loop with signature matching types dtype('<U32') dtype('<U32') dtype('<U32')

Traceback (most recent call last):

File "", line 1, in

test_score = mean_squared_error(test_y,predictions)

File "C:\Python34\lib\site-packages\sklearn\metrics\regression.py", line 232, in mean_squared_error

output_errors = np.average((y_true - y_pred) ** 2, axis=0,

TypeError: ufunc 'subtract' did not contain a loop with signature matching types dtype('<U32') dtype('<U32') dtype('<U32')

有什么办法吗？
Anthony of Sydney NSW

Jason Brownlee 2017年3月8日上午9:46 #

看来您需要将数据转换为浮点值。

例如，在numpy中可能是这样

X = X.astype('float32')

1

X = X.astype('float32')

回复

Anthony of Sydney who noticed that it was a string not a float 2017年3月8日上午5:30 #

尊敬的Jason博士，
解决了问题。您不能假设所有*.csv数字都是浮点数或整数。出于某种原因，这些数字似乎被引号括起来了。请注意，数据是sp500.csv，而不是上述练习的数据。
请注意，输出中的数字被引号括起来

test_y
array(['1.331', '1.412', '1.474', '1.559', '1.585', '1.788', '1.817'], dtype=object)
>>> predictions
['1.24', '1.331', '1.412', '1.474', '1.559', '1.585', '1.788']
>>> test_y = [float(i) for i in test_y] # convert string to float
>>> predictions = [float(i) for i in predictions]  # convert string to float
>>> test_score = mean_squared_error(test_y,predictions)
>>> test_score
0.009805285714285716

test_y

array(['1.331', '1.412', '1.474', '1.559', '1.585', '1.788', '1.817'], dtype=object)

>>> predictions

['1.24', '1.331', '1.412', '1.474', '1.559', '1.585', '1.788']

>>> test_y = [float(i) for i in test_y] # convert string to float

>>> predictions = [float(i) for i in predictions] # convert string to float

>>> test_score = mean_squared_error(test_y,predictions)

>>> test_score

0.009805285714285716

现在可以了，
此致
来自悉尼的安东尼

Jason Brownlee 2017年3月8日上午9:46 #

很高兴听到你解决了问题，Anthony。

回复

Anthony from Sydney 2017年3月8日上午6:07 #

尊敬的Jason博士，
问题已经解决。数组中的值是字符串，所以我必须将它们转换为字符串。

test_y
array(['1.331', '1.412', '1.474', '1.559', '1.585', '1.788', '1.817'], dtype=object)
>>> predictions
['1.24', '1.331', '1.412', '1.474', '1.559', '1.585', '1.788']

test_y

array(['1.331', '1.412', '1.474', '1.559', '1.585', '1.788', '1.817'], dtype=object)

>>> predictions

['1.24', '1.331', '1.412', '1.474', '1.559', '1.585', '1.788']

所以我将每个数组中的字符串转换为浮点数。

>>> test_y = [float(i) for i in test_y]
>>> predictions = [float(i) for i in predictions]
>>> test_score = mean_squared_error(test_y,predictions)
>>> test_score
0.009805285714285716

>>> test_y = [float(i) for i in test_y]

>>> predictions = [float(i) for i in predictions]

>>> test_score = mean_squared_error(test_y,predictions)

>>> test_score

0.009805285714285716

希望这能帮助其他尝试将值转换为适当数据类型以进行数值计算的人。
Anthony from Sydney NSW

Johnson S 2017年4月17日上午6:39 #

我如何将我的预测显示为日期，而不是日志，例如我每周都有事件编号数据集，我想预测下一周
第一周 669
第二周 443
第三周 555

所以在4月第一周，我想显示4月第一周和第二周的时间序列预测

回复
- Jason Brownlee 2017年4月18日上午8:28 #
  
  抱歉，我不太明白。也许您可以提供一个更完整的输入和输出示例？
  
  回复
Chika 2017年4月30日上午2:46 #

感谢这篇精彩的教程。我去年在Facebook上发现了您的文章。从那时起，我一直在关注您的所有教程，我必须承认，虽然我学习机器学习不到一年，但由于您在网站上发布的这些免费服务，我的知识基础得到了极大的增长。
再次感谢Jason博士的慷慨。

我的问题是，我已经仔细遵循了本文中关于我的数据集的所有步骤，该数据集在2个月内每10分钟记录一次。请问，对于预测未来7天或更长时间的值，哪个时间滞后是合适的。

根据我对时间序列应用的检验统计量和直方图，我的时间序列是平稳的。但我仍然不知道用一个每天每10分钟记录2个月的数据集能否得出合理的结论。

回复
- Jason Brownlee 2017年4月30日上午5:33 #
  
  为你的进步喝彩！
  
  这篇帖子为您提供了一些关于如何选择合适的q和p值（滞后变量）的想法。
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  希望这些能作为一个开始有所帮助。
  
  回复
Soy 2017年5月14日上午4:35 #

杰森博士，
非常感谢这篇帖子。我终于学会了如何将理论付诸实践。

回复
- Jason Brownlee 2017年5月14日上午7:33 #
  
  听到这个消息我很高兴，Soy，谢谢！
  
  回复
Akshit Mantri 2017年6月8日下午10:35 #

Jason博士，我如何预测AR模型的预测的低置信区间和高置信区间？

回复
- Jason Brownlee 2017年6月9日上午6:25 #
  
  这篇文章会有帮助：
  https://machinelearning.org.cn/time-series-forecast-uncertainty-using-confidence-intervals-python/
  
  回复
  - Akshit Mantri 2017年6月9日下午5:40 #
    
    谢谢你的回复。这是一篇非常好的帖子。但是，它是针对ARIMA模型的。我的ARIMA模型有一些问题，我无法使用它。AR模型是否有这样的置信区间预测？
    
    回复
    - Jason Brownlee 2017年6月10日上午8:18 #
      
      是的，我相信同样的方法适用。使用 forecast() 函数。
      
      回复
Daoud 2017年6月11日下午9:10 #

ValueError: On entry to DLASCL parameter number 4 had an illegal value
当我使用时，我发现上述错误
model = AR(train) ## 没有错误
model_fit = model.fit() ## 显示上述错误

回复
Samuel N 2017年6月15日上午6:10 #

感谢Jason的精彩文章。不过有一个问题，我感兴趣的是每n天对我的时间序列数据进行自回归。例如。选择前20天并预测第20天的值。然后选择接下来的20天（向后移1位）并预测第21天的值，依此类推，直到数据集结束。这在代码中如何实现？谢谢。

回复
- Jason Brownlee 2017年6月15日上午8:54 #
  
  考虑使用前向验证的一种变体
  https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
  
  回复
Dhineshkumar 2017年6月15日下午5:49 #

嗨，Jason，

感谢您的文章。我有一些疑问。

1) 我们是否只在时间序列平稳后才对自相关图和自相关函数进行分析？

2) 对于上面的时间序列，滞后=1时相关值最大。那么在进行自回归时，t-1处的值是否被赋予更大的权重？

3) 当AR模型说，对于滞后-29模型，MSE最小。这是否意味着由从t到t-29的值构建的回归模型给出了最小的MSE？

请澄清。

谢谢你

回复
- Jason Brownlee 2017年6月16日上午7:52 #
  
  1. 理想情况下，是的，在数据平稳后进行分析。
  
  2. 是的。
  
  3. 是的。
  
  回复
  - Dhineshkumar 2017年6月16日下午6:46 #
    
    谢谢。
    
    回复
    - Jason Brownlee 2017年6月17日上午7:24 #
      
      不客气。
      
      回复
TaeWoo Kim 2017年6月20日上午10:10 #

嘿，Jason。感谢这篇精彩的教程。

在这一行...

print('Lag: %s' % model_fit.k_ar)
print('Coefficients: %s' % model_fit.params)

“滞后”和“系数”的“通俗”解释是什么？

是不是“滞后”是AR模型确定显著性结束的点（即，在此数字之后，自相关不够“强”）并且系数是自相关的“强度”的零假设的p值？

回复
- Jason Brownlee 2017年6月21日上午8:08 #
  
  滞后观测是先前时间步长的观测。
  
  滞后系数是这些滞后观测的权重。
  
  回复
  - TaeWoo Kim 2017年6月22日上午5:03 #
    
    谢谢你，Jason。这个答案让我更困惑了。🙂
    
    你手动计算预测的那个部分……你指定了history.append(obs)。这意味着需要t0之前的测试数据才能预测t1吗？
    
    换句话说，这个模型只能预测1个时间周期之外的值吗？
    
    如果我错了，我该如何修改代码以预测多达n个周期之外的值？
    
    回复
  - TaeWoo Kim 2017年6月22日上午5:49 #
    
    我想我读完这个就回答了自己的问题... https://machinelearning.org.cn/multi-step-time-series-forecasting/
    
    您使用statsmodels.tsa.ar_model.AR给出的示例是用于单步预测的，我说的对吗？
    
    回复
    - Jason Brownlee 2017年6月22日上午6:13 #
      
      正确，但是 ARIMA (也可能是 AR) 的 forecast() 函数可以进行多步预测。它可能不太好。
      
      回复
Yigit Yazicioglu 2017年9月30日上午12:29 #

亲爱的Jason

感谢这个精彩的指南。我的数据集有问题，我正在深入研究时间序列建模。

我尝试建模一个物理模型，使得

y(t+1) = y(t) + f(a(t), b(t), c(t)) 与 AR 模型。

实际问题是使用基本热传递预测金属温度，其中 y 表示金属温度，f 是冷却剂质量流量、冷却剂温度、气体流量和气体温度等传感器数据的一个函数。

您建议使用哪种模型？

回复
- Jason Brownlee 2017年9月30日上午7:43 #
  
  听起来是个很好的问题。我建议测试一套不同的方法，看看哪种方法最适合您的特定数据，考虑到您的特定建模要求。
  
  我通常推荐这个过程
  https://machinelearning.org.cn/start-here/#process
  
  回复
Monika 2017年10月13日上午3:48 #

你好 Jason……
我读了你的几篇文章，觉得很有帮助。我是机器学习的新手，想问一下这些预测点的含义，例如 predicted=14.349246，这个值是什么意思？？？

它如何帮助理解预测？

如果您有发布过任何关于交叉回归的文章，也请发布一下。

回复
- Jason Brownlee 2017年10月13日上午5:50 #
  
  抱歉，我不明白。也许您可以重新措辞您的问题？
  
  回复
Shantanu 2017年10月16日上午6:30 #

感谢这篇精彩的文章。
我有一个问题：我们如何通过AR基于多列进行预测？
例如，有以下几列：
日期，定价，ABC，PQR
ABC，PQR有助于预测价格。所以我想基于这些列也预测定价。
谢谢你

回复
- Jason Brownlee 2017年10月16日下午3:46 #
  
  这可能是可行的，但我没有一个可用的例子，抱歉。
  
  回复
Ryan Berger 2017年10月22日上午4:00 #

如何使用 Keras 将其构建成一个深度自回归网络？

回复
- Jason Brownlee 2017年10月22日上午5:33 #
  
  一个深度MLP就能搞定！
  
  回复
Forouq 2017年11月10日上午3:28 #

感谢您的精彩教程
不过我有一个问题。根据 Pandas 的自相关图，当滞后为 1 时获得最大相关性。但 AR 模型选择滞后为 29 来构建自回归。
我在我的数据集上检查了这段代码，滞后为1的自回归在测试案例上表现得比AR模型选择的滞后为14的自回归好得多。你能解释一下吗？我原以为自相关检查的是线性关系，因此，将线性函数映射到数据的自回归应该在给出最大皮尔逊相关性的滞后变量上表现最好。

回复
- Jason Brownlee 2017年11月10日上午10:37 #
  
  也许该方法被数据中的噪声或小样本量所困扰？
  
  回复
Duplec 2017年11月19日上午12:45 #

如果日期中也包含时间怎么办？
1981-01-01,20.7 就像 1981-01-01 03:00:00,20.7

回复
- Jason Brownlee 2017年11月19日上午11:08 #
  
  当然可以。
  
  回复
sam 2017年11月26日上午11:46 #

嗨，很棒的教程。只是想问一下如何更改代码中的顺序或滞后？另外，如果有什么关于理解如何使用statsmodels库的教程，那就太好了。

回复
- Jason Brownlee 2017年11月27日上午5:46 #
  
  我的书是关于这个主题最好的资料来源
  https://machinelearning.org.cn/introduction-to-time-series-forecasting-with-python/
  
  你可以直接对代码进行差分，或者在ARIMA模型中使用d参数来控制差分阶数。我两者都有教程，也许可以从这里开始
  https://machinelearning.org.cn/start-here/#timeseries
  
  回复
At 2017年12月31日上午4:25 #

非常感谢！我在开发AR模型时遇到了一个问题，有些日期被丢弃了。我不得不提到频率参数，尽管我已经提供了日期时间

回复
- Jason Brownlee 2017年12月31日上午5:21 #
  
  有意思。它解决你的问题了吗？
  
  回复
Carolyn 2018年3月14日上午1:52 #

嗨，Jason，

优秀的文章！有没有可能写一篇关于如何用大数据进行向量自回归的博客文章？有时候LSTM是杀鸡用牛刀，即使是普通的RNN也可能是杀鸡用牛刀，所以如果能用简单的自回归就太好了。

Python中的VAR包可以做到这一点，但对于大型稀疏数据集来说，它很快就会遇到内存问题。

如果您知道其他向量自回归工具，任何见解都将不胜感激！

回复
- Jason Brownlee 2018年3月14日上午6:31 #
  
  谢谢你的建议，Carolyn。
  
  回复
Harshil 2018年4月23日下午7:04 #

亲爱的 Jason,

非常感谢您的精彩文章。我对数据驱动的预测有一个疑问。我需要预测电器能耗，它取决于26个变量。我有3个月的电器能耗数据以及26个变量的数据。借助这26个变量，我如何预测未来的电器能耗？

回复
- Jason Brownlee 2018年4月24日上午6:27 #
  
  好问题。
  
  你可以将数据转换为监督学习问题，并尝试一系列机器学习算法
  https://machinelearning.org.cn/convert-time-series-supervised-learning-problem-python/
  
  我希望将来能提供更多关于这个主题的信息。
  
  回复
Praveen 2018年5月27日下午10:21 #

嘿，杰森！
感谢您的文章。我对此有一个疑问。如何预测数据集中不存在的未来日期？

回复
- Jason Brownlee 2018年5月28日上午5:59 #
  
  调用 model.predict() 并指定日期或索引。
  
  本教程将向您展示如何操作
  https://machinelearning.org.cn/make-sample-forecasts-arima-python/
  
  回复
Ashish 2018年6月21日下午5:43 #

能否提供一个关于VAR模型的详细示例？

回复
- Jason Brownlee 2018年6月22日上午6:03 #
  
  我希望将来能涵盖这种方法，感谢你的建议。
  
  回复
Bhaskar Sharan 2018年7月10日下午6:29 #

from pandas import Series
from matplotlib import pyplot
series = Series.from_csv(‘G:\Study_Material\daily-minimum-temperatures.csv’)
print(series.head())
series.plot()
pyplot.show()

出现错误：“空‘DataFrame’：没有数字数据可绘制”

如何解决这个问题，先生？

回复
- Jason Brownlee 2018年7月11日上午5:53 #
  
  也许重新检查一下你是否正确加载了数据？
  
  回复
Vijay 2018年7月30日上午10:53 #

这是一篇非常精彩的帖子，我偶然发现它，非常感谢您提供了这么多内容和精彩的例子。我是机器学习的新手，我有一个关于在稀疏时间序列中使用ARIMA的问题。我有一些事件可能每天、每周、每几周或每月发生一次。典型的例子可能是商务会议。不同的会议可能以不同的频率发生。使用ARIMA来预测潜在模式是否合适？我现实世界的问题涉及根据虚拟会议的历史预测其规模。假设有一个像Hangout这样的服务。我正在尝试查看ARIMA是否是根据其历史预测虚拟会议资源需求的合适算法。我根据这个教程尝试了ARIMA，但结果并不令人信服。我不确定将这个问题建模为时间序列问题是否合适，以及ARIMA是否是解决此类问题的好选择。

回复
- Jason Brownlee 2018年7月30日下午2:16 #
  
  也许可以把它作为一个起点来尝试。
  
  回复
Tim Boons 2018年8月7日下午6:53 #

我正在尝试建立一个AR模型，使用滞后192来预测一个序列。

该序列每15分钟有一个数据点，但您在测量后的第二天收到数据。
所以您必须用前一天 (D-1) 的数据预测第二天 (D+1)，因此数据点之间存在192个滞后，每个滞后间隔15分钟。

有没有办法将AR()函数限制为t-192之前的所有数据点？

回复
- Jason Brownlee 2018年8月8日上午6:16 #
  
  也许可以直接在您选择的滞后上拟合一个正则化线性回归模型？
  
  回复
  - Tim Boons 2018年8月14日下午10:14 #
    
    感谢您的回复！
    
    在哪里可以找到关于正则化线性回归模型的更多信息？
    
    回复
    - Jason Brownlee 2018年8月15日上午6:02 #
      
      任何一本好的机器学习书籍，例如
      https://amzn.to/2KSoQ0a
      
      回复
Kamal Pokharel 2018年8月27日下午4:54 #

非常感谢这篇可爱的文章

回复
- Jason Brownlee 2018年8月28日上午5:57 #
  
  谢谢，很高兴它有帮助。
  
  回复
Allison 2018年8月28日下午1:00 #

布朗利博士，您好，

非常棒的文章——我一步步跟着做，很有帮助。

在这一步
model.fit()

我收到此错误
TypeError: 找不到共同的数据类型。

这可能来自哪里？

回复
- Jason Brownlee 2018年8月29日上午7:59 #
  
  这很奇怪。你用的是教程中的代码和数据吗？
  
  你替换数据文件中的“?”字符了吗？
  
  回复
Phil 2018年9月29日上午4:49 #

你的第一个方程不应该是

X(t) = b0 + b1*X(t-1) + b2*X(t-2)

而不是

X(t+1) = b0 + b1*X(t-1) + b2*X(t-2)

回复
- Jason Brownlee 2018年9月29日上午6:38 #
  
  那“t”在哪里？
  
  回复
  - asieh 2019年8月28日上午6:30 #
    
    我也有和Phil一样的问题，我不确定你说的回答是什么意思。当你写道：“我们可以根据过去两个时间步（t-1和t-2）的观测值来预测下一个时间步（t+1）的值”时，对于（t+1）来说，过去两个时间步应该是t和t-1，而不是t-1和t-2。
    你为什么跳过t？
    
    回复
    - asieh 2019年8月28日上午6:35 #
      
      另外，在下面的句子中你以正确的方式说了它
      
      “我们可以将前一个时间步（t-1）的观测值与下一个时间步（t+1）的观测值绘制成散点图。”
      
      所以你谈论的是当前时间 (t) 与前一步 (t-1) 与下一步 (t+1)。
      
      这就是为什么我认为公式不应该像Phil提到的那样。
      
      回复
      - Jason Brownlee 2019年8月28日上午6:45 #
        
        是的，谢谢。
ML Uros 2018年10月12日上午2:12 #

嗨，Jason。你的博客和这篇文章做得太棒了！
我想知道你是否能帮我解决以下问题：在你的例子中，你选择7个点作为测试集，AR模型在这些点上的MSE低于持久性模型。但是，如果我把测试集放大，比如几百个点，并进行AR预测，我得到的AR模型的MSE会更高。我知道几百个点意味着大约一年的数据点，AR模型可以在其间更新以获得更好的结果，但我只是想知道你对此的看法。这是否意味着AR模型不适合预测太远的未来？
另外，如果我使用AR模型预测大约180个点，AR的MSE值会显著上升，大约到9。有趣的是，如果测试集甚至扩大到大约350个点，MSE值会下降到大约7。持久性模型的MSE变异性较低。这种变化的MSE说明了数据和应用AR的什么问题？

回复
- Jason Brownlee 2018年10月12日上午6:42 #
  
  你预测的未来越远，性能越差。
  
  回复
Dieu Do 2018年10月13日下午1:54 #

你好，Jason Brownlee 博士，

非常感谢您的优秀文章。
我有一个关于预测结果的问题。
为什么第 i 个点的预测解与第 (i-1) 个点的预期解非常接近？
在您的大部分文章中，我都看到了这一点。
我不明白为什么？你能帮我回答这个问题吗？

非常感谢 Jason Brownlee 博士。

祝好，
Dieu Do

回复
- Jason Brownlee 2018年10月14日上午6:02 #
  
  这是我在这里回答的一个常见问题
  https://machinelearning.org.cn/faq/single-faq/why-is-my-forecasted-time-series-right-behind-the-actual-time-series
  
  回复
Yingfei 2018年10月22日上午1:21 #

嗨，Jason，感谢你的分享。

我正在尝试使用AR模型来预测一个复数值时间序列。我使用了如下序列，并替换了你示例代码中的温度数据

series = Series([1, 1+1j, 2, 3, 4, 5, 8, 1+2j, 3, 5])

然而，它报告了如下错误信息

/anaconda/lib/python3.6/site-packages/statsmodels/tsa/tsatools.py in lagmat(x, maxlag, trim, original, use_pandas)
377 dropidx = nvar
378 if maxlag >= nobs
–> 379 raise ValueError(“maxlag should be < nobs")
380 lm = np.zeros((nobs + maxlag, nvar * (maxlag + 1)))
381 for k in range(0, int(maxlag + 1))

ValueError: maxlag should be < nobs

请指教如何纠正它。

谢谢。

回复
- Jason Brownlee 2018年10月22日上午6:20 #
  
  该错误表明您可能需要更改模型的配置以适应您的数据。
  
  回复
NikosLamp 2018年11月22日上午9:38 #

你好，

在“快速检查自相关”部分，您将数据向后移动了一个位置，并将列命名为“t-1”和“t+1”。在文章“https://machinelearning.org.cn/convert-time-series-supervised-learning-problem-python/”的“Pandas shift() 函数”部分，您有一行代码：“df['t-1'] = df['t'].shift(1)”，表示移动一个位置意味着1个时间差（t-1，t）。您能解释一下哪个是正确的吗？我错过了什么？

谢谢

回复
- Jason Brownlee 2018年11月22日下午2:10 #
  
  实际上它应该是't'和't-1'。
  
  回复
Yannick 2018年12月13日下午9:24 #

布朗利博士，您好，

我使用了你的教程来对一个数据集进行预测，该数据集记录了2017年每分钟使用的停车位数量。对于持久性模型，我得到一个12.7的测试MSE分数，对于自回归模型，我得到一个74的测试MSE分数。你能告诉我这是好还是坏吗？同时，你能给我更多关于你的代码中MSE结果如何工作的细节吗？它是否在整个数据集上运行？

此致。

回复
- Jason Brownlee 2018年12月14日上午5:30 #
  
  好坏只能通过与持久性模型进行比较才能得知。
  
  你可以自己回答这个问题。
  
  74 > 12 == 坏。
  
  回复
Awibawa 2018年12月20日下午1:16 #

布朗利博士，您好，
有没有NARX（带外生输入的非线性自回归）的参考文献和示例代码？如果这偏离主题，我很抱歉，也许你在这方面有经验

此致，

回复
- Jason Brownlee 2018年12月20日下午2:02 #
  
  不确定，抱歉。
  
  回复
Markus 2018年12月23日下午10:07 #

当我们说一个给定模型使用滞后值3时，以下哪个是给定模型的方程

X(t) = b0 + b1*X(t-1) + b2*X(t-2)+ b3*X(t-3)
X(t) = b0 + b3*X(t-3)

我猜是第一个，但我不确定。

回复
- Jason Brownlee 2018年12月24日上午5:29 #
  
  它将是预测步骤前三个时间步的线性函数。
  
  线性函数的具体形式会因算法而异。
  
  回复
Victor 2019年2月25日上午1:45 #

嗨，Jason，

如何使用此代码更改AR模型的顺序。

例如AR(1)，AR(2)等？

回复
- Jason Brownlee 2019年2月25日上午6:46 #
  
  创建AR模型并为阶数提供一个整数。
  
  回复
  - Victor 2019年2月25日上午9:12 #
    
    我不太明白你的意思？
    
    我只是想知道如何根据你给出的例子来做。难道不就是一行代码，我将额外的参数添加为“order number”吗？
    
    回复
    - Victor 2019年2月25日下午1:28 #
      
      model = AR(train, order = 1)
      
      是这样吗，基于上面的代码
      
      回复
      - Jason Brownlee 2019年2月25日下午2:19 #
        
        是的，在fit()函数上使用maxlag，或者使用不带d或q元素的ARIMA。
    - Jason Brownlee 2019年2月25日下午2:15 #
      
      我明白了，是的，你可以在调用 fit() 时设置“maxlag”参数。更多信息在这里
      https://statsmodels.cn/devel/generated/statsmodels.tsa.ar_model.AR.fit.html#statsmodels.tsa.ar_model.AR.fit
      
      或者，你可以使用 ARIMA 并将阶数设置为 (n, 0, 0)。
      
      回复
WiseNetAI 2019年3月6日上午6:02 #

您能否解释一下为什么将时间步的观测值追加到历史列表中不算“作弊”？这难道不相当于将模型试图预测的部分数据喂给模型吗？这在现实生活中可能吗，即我们可能不知道我们试图预测的事物的实际值？我指的是生成“滚动AR模型预测”的代码中的第26行。如果您能为此启发我，我将不胜感激。谢谢。

回复
- Jason Brownlee 2019年3月6日上午8:00 #
  
  不行。
  
  这被称为滚动向前验证，在该模型下，我们假设真实观测值在预测之后可用，并反过来可供模型使用。
  
  如果这个假设不适用于你的数据，你可以设计一个滚动向前验证策略来捕捉你特定预测问题的假设。
  
  更多关于滚动向前验证的信息在这里
  https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
  
  回复
  - WiseNetAI 2019年3月7日上午11:32 #
    
    谢谢你。这帮助我解决了我的不确定性。
    
    回复
Nihar Dharia 2019年3月16日上午1:17 #

你好，

model.predict(start, end) 总是给我相同的值，结果得到一条直线预测。所以我使用了上面显示的历史方法，并不断将yhat添加到测试中，以获取我想要的样本外预测数量（代码如下）。这正确吗？

for t in range(len(test)+number_of_values_to_predict)
length = len(history)
lag = [history[i] for i in range(length-window,length)]
yhat = coef[0]
for d in range(window)
yhat += coef[d+1] * lag[window-d-1]
obs = test[t]
predictions.append(yhat)
history.append(obs)
test = np.append(test,yhat)

回复
- Jason Brownlee 2019年3月16日上午7:55 #
  
  我不太清楚你想要实现什么？
  
  回复
  - Nihar Dharia 2019年3月16日上午11:01 #
    
    我正在尝试实现样本外预测，例如预测未来7天的值。使用predict()给我相同的预测值，并给出一条直线预测。因此我尝试使用上面的代码。你认为这样做正确吗？
    
    回复
    - Jason Brownlee 2019年3月17日上午6:15 #
      
      也许尝试不同的模型或使用不同的数据？
      
      回复
Maysaa 2019年4月4日下午6:38 #

嗨，Jason，
你只在只有单个标签或单个输入（即相同输出的以前记录）的情况下提供自回归模型。如果例如我们关注房屋能耗的预测，并且我们有不同的输入标签，如室内温度、室外温度，并考虑房屋结构和以前的记录，那该怎么办？
我们如何开发这样的模型？
你有没有这方面的例子？
谢谢你

回复
- Jason Brownlee 2019年4月5日上午6:13 #
  
  好问题，我将此称为多元时间序列问题，你可以在这里找到示例
  https://machinelearning.org.cn/start-here/#deep_learning_time_series
  
  回复
Haiyang Duan 2019年4月17日上午10:54 #

嘿 Jason，我正在用我的数据集遵循你的教程。但我对结果有一些疑问。(1)滞后（即 model_fit.k_ar 的值）对你的数据集意味着什么？(2)“Pandas 自相关图”的周期是什么意思？你能花点时间告诉我一些关于它们的信息吗？非常感谢。

回复
- Jason Brownlee 2019年4月17日下午2:45 #
  
  滞后是一个先前的观测值，也许这会有所帮助
  https://machinelearning.org.cn/time-series-forecasting-supervised-learning/
  
  更多关于自相关的信息在这里
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  回复
  - Haiyang Duan 2019年4月20日上午11:50 #
    
    您能解释一下滞后（model_fit.k_ar）与数据集周期之间的关系吗？
    
    回复
    - Jason Brownlee 2019年4月21日上午8:18 #
      
      怎么会呢？
      
      回复
  - Haiyang Duan 2019年4月20日下午12:31 #
    
    或者除了快速傅里叶变换，我如何获得时间序列数据集的周期？
    
    回复
    - Jason Brownlee 2019年4月21日上午8:19 #
      
      明白了，你可以查看一下序列图。
      
      你可以使用领域知识。
      
      你可以对一个简单的多项式函数使用网格搜索。
      
      回复
Dav 2019年4月24日下午8:39 #

嗨

感谢这篇有用的文章。我在哪里可以获得数据文件“daily-minimum-temperatures.csv”？当我点击“在此处了解有关数据集的更多信息”时，我无法访问目标网站。

谢谢

回复
- Jason Brownlee 2019年4月25日上午8:11 #
  
  你可以直接从这里下载
  https://raw.githubusercontent.com/jbrownlee/Datasets/master/daily-min-temperatures.csv
  
  回复
  - Dav 2019年5月1日上午3:15 #
    
    收到，谢谢你的帮助
    
    回复
Thibault de Wit 2019年6月6日上午5:10 #

嗨，Jason，

这里有个小问题。为什么我们的训练数据集从1开始而不是0？

在你的代码中，我们有：`train, test = X[1:len(X)-7], X[len(X)-7:]`
但是使用 `train, test = X[:len(X)-7], X[len(X)-7:]` 这样会允许模型多训练一个值（从索引0开始而不是从索引1开始）。

回复
- Jason Brownlee 2019年6月6日上午6:39 #
  
  谢谢。不确定我当时在想什么……
  
  回复
Martin Muñoz Mandujano 2019年7月2日下午12:41 #

嗨，Jason，
代码中AR模型的阶数是多少？
或者阶数是如何定义的？

回复
- Jason Brownlee 2019年7月2日下午2:10 #
  
  阶数是模型考虑的滞后观测值的数量。
  
  你可以对不同的值进行网格搜索，或者使用ACF/PACF图来选择值。
  
  回复
Ank 2019年7月28日下午7:07 #

嗨，Jason，
我是Python新手，这是pandas的更新问题吗？

我无法运行“快速检查自相关：”的代码

除非添加以下两行代码

Data[‘Date’] = pd.to_datetime(Data[‘Date’])
series=pd.Series(Data[‘Temp’])

lag_plot(series)
pyplot.show()

谢谢你

回复
- Jason Brownlee 2019年7月29日上午6:12 #
  
  很抱歉听到这个消息，你具体遇到了什么问题？
  
  我有一些建议可能会有所帮助
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
Leo Barbosa 2019年7月29日上午10:11 #

嗨，Jason，

感谢您的教程，非常有帮助。但我有一个问题

您的最后一个例子（滚动预测）与statsmodels.tsa.ar_model.AR.predict()在dynamic=False时所做的有什么不同？
据我理解，它会做您在最后一个例子中所做的事情，但您得到了不同的结果，所以我不知道我错过了什么。

来自statsmodels网站
“dynamic 关键字会影响样本内预测。如果 dynamic 为 False，则使用样本内滞后值进行预测。如果 dynamic 为 True，则使用样本内预测代替滞后因变量。第一个预测值是开始。”

回复
- Jason Brownlee 2019年7月29日下午2:21 #
  
  谢谢。
  
  我相信动态只影响“样本内”数据，例如训练数据范围内的数据。
  
  回复
Manpreet Singh 2019年9月9日上午8:49 #

嗨，Jason，

感谢您的教程，非常有帮助。但我有一个问题

您写道：“statsmodels 库提供了一个自回归模型，该模型使用统计测试自动选择合适的滞后值并训练线性回归模型。”

它是否使用AIC、BIC等模型选择标准来选择合适的滞后值，还是近似所有模型并选择MSE最小的模型？

回复
- Manpreet Singh 2019年9月9日上午9:17 #
  
  fit([maxlag, method, ic, trend, …])
  
  您能否解释一下在您的示例中我们向此函数传入的所有输入。当我们调用 model.fit( ) 时，maxlag、method 和 ic 是什么？
  
  回复
  - Jason Brownlee 2019年9月9日下午1:54 #
    
    maxlag 是拟合模型时要考虑的最大输入滞后。
    
    其他参数在这里描述
    https://statsmodels.cn/stable/generated/statsmodels.tsa.ar_model.AR.fit.html#statsmodels.tsa.ar_model.AR.fit
    
    回复
- Jason Brownlee 2019年9月9日下午1:53 #
  
  谢谢，很高兴对您有帮助。
  
  好问题，你可以在这里了解更多关于它如何工作的信息
  https://statsmodels.cn/stable/generated/statsmodels.tsa.ar_model.AR.fit.html#statsmodels.tsa.ar_model.AR.fit
  
  回复
George 2019年9月11日上午4:43 #

嗨，Jason，
你知道验证AR模型的方法是什么吗？
可以进行哪些具体测试来证明开发的模型是有效的？

回复
- Jason Brownlee 2019年9月11日上午5:43 #
  
  是的，滚动预测验证（walk-forward validation）
  https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
  
  回复
Leo 2019年9月24日下午2:56 #

嗨，Jason，

感谢您的教程，非常有帮助。我有一个问题，在这种情况下您的ACF滞后很大，我的也是。如果ACF或PACF的滞后非常大，我们如何决定选择ARIMA参数？在我的情况下，我的ACF在滞后1000处趋近于零，PACF在滞后30处趋近于零。

回复
- Jason Brownlee 2019年9月25日上午5:50 #
  
  很好的问题，我在这里给出了一些关于如何从 ACF/PACF 图选择 ARIMA 参数的一般建议
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  回复
Laguna 2019年10月16日上午4:31 #

感谢您的文章。
偏自相关（PACF）图不是应该用于确定AR模型的统计显著滞后系数吗？ACF不是用于移动平均部分，而不是ARMA模型的AR部分吗？我对使用ACF图作为模型AR部分的选择感到困惑

回复
- Jason Brownlee 2019年10月16日上午8:12 #
  
  请看这个教程
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  回复
karan 2020年2月10日下午6:11 #

你好杰森。解释得非常清楚。

回复
- Jason Brownlee 2020年2月11日上午5:08 #
  
  谢谢！
  
  回复
Evan Berry 2020年3月2日上午8:59 #

你好 Jason，我想知道这种滞后变量技术是否可以用于其他特征。所以看起来你上面正在预测天气，所以你使用了天气数据的滞后变量。如果我们想使用另一个变量（例如每天的总日照量）的滞后变量呢？即使这是一个不同的变量，你是否可以使用相同的滞后数据技术来预测天气？

回复
- Jason Brownlee 2020年3月2日上午10:07 #
  
  是的，它对任何时间序列数据都很有用。
  
  回复
Mark 2020年3月28日上午1:18 #

嗨 Jason

我正在尝试使用OLS进行动态预测。该模型有一个AR(1)变量和n个外生变量。

我使用for循环对不同的外生变量组合运行多次回归并将结果存储起来。我将数据分成测试/训练集，并在测试集上运行预测并存储MAE和RMSE。

我遇到的问题是样本外测试使用的是实际的滞后AR(1)变量，而不是动态生成的。我希望使用外生变量的实际值，但使用动态估计的AR(1)变量。

您对此有任何关于最佳做法的建议吗？我已将SARIMAX作为替代方案进行了研究，但理想情况下想使用OLS。

另外，您会推荐哪本关于statsmodels/OLS/时间序列预测的书？

您有没有关于Python中蒙特卡罗模拟的资料？

谢谢

Mark

回复
- Jason Brownlee 2020年3月28日上午6:24 #
  
  抱歉，我不明白你具体遇到的问题。“生成”是指递归模型中的预测吗？
  
  我在这本书中介绍了ARIMA时间序列预测的基础知识（不包括外生变量或SARIMA）
  https://machinelearning.org.cn/introduction-to-time-series-forecasting-with-python/
  
  Python中关于MC的不多
  https://machinelearning.org.cn/monte-carlo-sampling-for-probability/
  
  以及
  https://machinelearning.org.cn/markov-chain-monte-carlo-for-probability/
  
  回复
  - Mark 2020年3月28日上午9:16 #
    
    感谢您的链接，Jason。
    
    我的意思是，statsmodels.predict() 的标准工作方式是，如果方程中存在 AR 项，则使用测试数据中实际的滞后因变量进行固定预测。对于真正的样本外预测，在给定的假设外生数据集或场景下，我希望预测对于方程中的 AR 项是动态的。否则，样本外预测结果看起来比实际情况要好。
    
    回复
    - Jason Brownlee 2020年3月29日上午5:48 #
      
      抱歉，我不太明白。也许你可以重新措辞你的问题/困惑？
      
      回复
Vasiliki Voukelatou 2020年4月1日上午12:32 #

嗨 Mark，非常棒的教程，非常感谢，

当使用 plot_acf(series, lags=30) 时，我不明白为什么自相关图会显示两次。
是不是有bug？

提前感谢您的回复。

回复
- Jason Brownlee 2020年4月1日上午5:51 #
  
  马克？
  
  很抱歉听到你遇到麻烦，也许这会有所帮助
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
  - Vasiliki Voukelatou 2020年4月1日下午9:35 #
    
    嗨 Jason :)，谁说了 Mark :P，
    
    非常感谢，解决了 :)
    
    回复
    - Jason Brownlee 2020年4月2日上午5:50 #
      
      你在评论中提到了
      
      “嗨 Mark，非常棒的教程，非常感谢，”
      
      很高兴听到你解决了问题。
      
      回复
Arabzai 2020年4月17日下午7:29 #

你好，
我们可以用支持向量回归代替线性回归吗？
如果可能的话，具体步骤是什么？我们如何从SVR-AR(1)模型中获取残差？
期待您的回复。
祝好，
阿拉伯扎伊

回复
- Jason Brownlee 2020年4月18日上午5:45 #
  
  是的，使用这个来准备你的数据
  https://machinelearning.org.cn/convert-time-series-supervised-learning-problem-python/
  
  回复
Olly Price 2020年4月19日上午7:49 #

你好，你知道 statsmodels.tsa.ar_model.AR() 在底层使用什么统计方法来确定 AR 的最优阶数吗？（似乎在文档中找不到任何内容。）

如果没有，您推荐我阅读哪些模型？我很欣赏您可以观察 ACF 并定性地确定一个大概的数字。

回复
- Jason Brownlee 2020年4月19日上午8:09 #
  
  AR模型不会优化阶数，你必须在调用fit()函数时指定阶数。
  
  你可以使用网格搜索来调整模型在你的数据上的表现，这里有一个例子
  https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
  
  回复
  - Olly Price 2020年4月19日上午8:58 #
    
    如果AR模型不优化阶数，那么model.fit.k_ar是从哪里来的？
    
    在教程中
    
    model = AR(train)
    model_fit = model.fit( )
    print(“滞后: %s” % model_fit.k_ar)
    >>> 滞后: 29
    
    滞后29是从哪里来的？
    
    回复
    - Jason Brownlee 2020年4月19日上午9:05 #
      
      看起来它使用配置的准则测试了不同的滞后值，在这里了解更多信息
      https://statsmodels.cn/stable/generated/statsmodels.tsa.ar_model.AR.fit.html#statsmodels.tsa.ar_model.AR.fit
      
      回复
Robert Gadzai 2020年5月17日上午2:25 #

非常感谢 Jason，你帮了我大忙

回复
- Jason Brownlee 2020年5月17日上午6:37 #
  
  不客气！
  
  回复
Lucas 2020年6月7日下午7:26 #

你好，

我正在尝试按照步骤操作，但在statsmodels方面遇到了问题。我的所有依赖项都已更新，但我无法导入statsmodels，并出现错误
ImportError: cannot import name ‘assert_equal’ from ‘statsmodels.compat.pandas’

你知道我该怎么做吗？

谢谢

回复
- Jason Brownlee 2020年6月8日上午6:09 #
  
  或许再次确认pandas和statsmodels是否已更新？
  
  我的版本是
  
  pandas: 1.0.3 statsmodels: 0.11.1
  
  1
  2
  
  pandas: 1.0.3
  statsmodels: 0.11.1
  
  回复
Ashwin 2020年6月25日下午11:28 #

我想问一下 AR(lags=10) 模型是否等于 ARMA(10,0)

回复
- Jason Brownlee 2020年6月26日上午5:36 #
  
  是的，我期望如此。
  
  回复
Emy 2020年6月30日上午12:46 #

你好，我如何知道正确的滞后数量？

回复
- Jason Brownlee 2020年6月30日上午6:28 #
  
  如果你不确定，可以测试一系列值，并使用能够使模型表现最佳的滞后观测值数量。
  
  回复
  - Cyril 2020年9月2日上午3:57 #
    
    你好，您会推荐使用“statsmodels.tsa.ar_model.ar_select_order”来选择最佳滞后期吗，因为“statsmodels.tsa.ar_model.AR”现在已被弃用？
    
    回复
    - Jason Brownlee 2020年9月2日上午6:34 #
      
      我不熟悉 statsmodels.tsa.ar_model.ar_select_order
      
      AutoReg 是一个合适的替代品
      https://statsmodels.cn/stable/generated/statsmodels.tsa.ar_model.AutoReg.html
      
      回复
krishnadas 2020年7月5日上午3:16 #

很好的例子。这帮助我开始了我的VAR模型项目。在这里，我使用多变量时间序列和statsmodel的VAR模型。正如您所提到的，API不会为新的观测值更新系数。由于它是多变量时间序列，我如何才能获得长期（例如6个月）的预测？

回复
- Jason Brownlee 2020年7月5日上午7:07 #
  
  我相信你可以随心所欲地调用 forecast() 和 predict。
  
  然后，当你得到新数据时，重新拟合模型。
  
  回复
Dilip Thosar 2020年7月27日下午10:35 #

在大多数实际案例中，除了时间序列之外，我们还有一些“可回归”变量。
这些变量不具有统一的周期性（季节性），通常在我们控制之下。例如，在零售店销售预测应用程序中，“礼品促销方案（Y/N）”或“方案折扣百分比（%或$）”可能会显著影响输出变量——销售额。只运行时间序列模型将忽略方案的影响。如何处理这些情况？

回复
- Jason Brownlee 2020年7月28日上午6:42 #
  
  它们可以作为线性模型的外生变量包含在内。
  
  回复
Sada Narayanappa 2020年8月21日上午8:22 #

当我运行

from pandas import read_csv
from matplotlib import pyplot
from statsmodels.tsa.ar_model import AutoReg
from sklearn.metrics import mean_squared_error
from math import sqrt
# 加载数据集
series = read_csv(‘daily-minimum-temperatures.csv’, header=0, index_col=0, parse_dates=True, squeeze=True)
# 分割数据集
X = series.values
train, test = X[1:len(X)-7], X[len(X)-7:]
# 训练自回归模型
model = AutoReg(train, lags=29)

我收到以下错误：

—————————————————————————
TypeError Traceback (most recent call last)
in
11 train, test = X[1:len(X)-7], X[len(X)-7:]
12 # train autoregression
—> 13 model = AutoReg(train, lags=29)
14 model_fit = model.fit()
15 print(‘Coefficients: %s’ % model_fit.params)

~/anaconda3/lib/python3.7/site-packages/statsmodels/tsa/ar_model.py in __init__(self, endog, lags, trend, seasonal, exog, hold_back, period, missing)
163 hold_back=None, period=None, missing=’none’)
164 super(AutoReg, self).__init__(endog, exog, None, None,
–> 165 missing=missing)
166 self._trend = string_like(trend, ‘trend’,
167 options=(‘n’, ‘c’, ‘t’, ‘ct’))

~/anaconda3/lib/python3.7/site-packages/statsmodels/tsa/base/tsa_model.py in __init__(self, endog, exog, dates, freq, missing, **kwargs)
44 def __init__(self, endog, exog=None, dates=None, freq=None,
45 missing=’none’, **kwargs)
—> 46 super(TimeSeriesModel, self).__init__(endog, exog, missing=missing,
47 **kwargs)
48

TypeError: super(type, obj): obj must be an instance or subtype of type

回复
- Jason Brownlee 2020年8月21日上午8:23 #
  
  听到这个消息我很难过。
  
  这可能有帮助
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
Giuseppe 2020年10月14日上午1:24 #

你好 Jason，感谢你的文章。

我有一个问题，在 AutoReg(train, lags=29) 指令中，lags 参数等于 29 是因为在 ACF 图中我们注意到高达 29 个时间步有很强的相关性吗？
考虑 PACF 图不是更好吗？

谢谢您的回答。

回复
- Jason Brownlee 2020年10月14日上午6:21 #
  
  正确。
  
  请参阅关于ACF/PACF图的这篇内容
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  回复
Muhammad Zubair 2020年12月6日上午3:53 #

你好，

解释得很清楚，但我想要澄清一下，时间滞后t-1是指一个时间滞后，你指的是当前时间t+1。那么你为什么不把它看作t和t+1或者t-1和t呢？

我知道这是一个非常基本的问题，但感谢您的回答。

回复
- Jason Brownlee 2020年12月6日上午7:10 #
  
  这是一个好主意，我应该那样做。
  
  回复
Girish 2021年3月21日上午1:16 #

嗨，Jason，

感谢这篇非常好的文章。我正在尝试执行以下操作，您能否提出建议/指导我。

我的原始数据如下

月份价格
2011-01-01 1405.07
2011-02-01 408.58
2011-03-01 277.75
2011-04-01 294.81
2011-05-01 511.77
2011-06-01 515.90

我需要预测价格（通过回归），考虑滞后5，并使用重建的数据集，如下所示，我需要预测第5个元素（X）的值

数据集 = [1405,408,277,294,X]
[408,277,294,511,X]
[277,294,511,515,X]

我该如何实现呢？

提前感谢
-Girish

回复
- Jason Brownlee 2021年3月21日上午6:10 #
  
  也许可以从这里开始学习时间序列预测的基础知识
  https://machinelearning.org.cn/start-here/#timeseries
  
  回复
Adarsh Krishna S 2021年5月6日下午11:09 #

你好，

我想要一个使用自回归模型进行EEG信号预测的代码，那么这个温度预测需要进行哪些更改呢？我正在使用Jupyter Notebook以及MNE和Pandas进行操作。
请帮帮我。

回复
- Jason Brownlee 2021年5月7日上午6:27 #
  
  也许可以尝试为您的数据集开发一个ARIMA或SARIMA模型，并将结果与其他方法进行比较。
  
  这可能是一个很好的起点
  https://machinelearning.org.cn/start-here/#timeseries
  
  回复
  - Adarsh 2021年5月7日下午3:56 #
    
    先生，这是我的项目。我需要EAR模型的代码来完成我的项目。所以我一直在搜索与脑电图相关的AR模型，并想将AR修改为EAR，但我找不到与脑电图相关的代码。您能帮我一下吗？
    
    回复
    - Jason Brownlee 2021年5月8日上午6:32 #
      
      抱歉，我不能为您编写代码。
      
      也许您可以根据您的特定数据集调整博客上的一个示例。
      
      回复
Adarsh Krishna S 2021年5月10日下午4:47 #

先生，
我用脑电图数据集尝试了您的自回归代码，输出与预期值和预测值完全不同。有什么解决方案吗？

回复
- Jason Brownlee 2021年5月11日上午6:39 #
  
  也许尝试一些数据准备？
  也许尝试另一种配置？
  也许尝试替代模型？
  
  回复
Will Zhao 2021年5月23日上午7:52 #

你好 Jason，

您知道如何修改模型设置，以便我们可以对系数矩阵A施加约束吗？例如，在VAR(1)中，Yt = (A1) (Yt-1) + E，A1= [a11, a12; a21, a22]，如何在运行模型之前强制a21 = 0，因为我已经知道一个格兰杰因果关系，而不是反过来？我还希望格兰杰因果关系检验也能反映这一点。您知道解决方案吗？

谢谢

回复
- Jason Brownlee 2021年5月24日上午5:39 #
  
  抱歉，我暂时不清楚。这可能需要自定义代码。
  
  回复
Shushman 2021年6月26日上午4:53 #

非常感谢您提供的有用入门资料！我发现最后代码块的第18-30行有点过于冗长，部分原因是历史记录最终是一个1长度数组的数组，而不是一个扁平数组。
我将该块重写如下以获得相同的输出：

history = train[len(train)-window:].flatten() predictions = list() for (t, obs) in enumerate(test.flatten()): hist_len = len(history) lag = np.concatenate(([1.0], np.flip(history[hist_len-window:]))) prediction = np.dot(coef, lag) predictions.append(prediction) history = np.append(history, obs) print('predicted=%f, expected=%f' % (prediction, obs))

回复
- Jason Brownlee 2021年6月26日上午5:00 #
  
  不客气。
  
  感谢分享！
  
  回复
Naser 2021年8月9日上午6:56 #

嗨，Jason，

我们能用这种方法生成场景吗？我的意思是几种随机场景。

谢谢

回复
- Jason Brownlee 2021年8月10日上午5:25 #
  
  是的，博客上有很多例子，您可以使用搜索框。
  
  回复
Jason 2021年8月22日上午3:07 #

感谢您提供这些信息。考虑到这篇文章已经有4年了，它对AR模型提供了非常好的解释。不过我有一个问题，我一直在使用statsmodel上的ARIMA函数，滞后和阶数是一样的吗？也就是说，您正在使用过去29个时间序列的自相关来预测下一个值吗？所以这会得到一个AR(29)模型吗？

回复
- Adrian Tam 2021年8月23日上午5:10 #
  
  如果您指的是其中的一个示例，那么您是对的。
  
  回复
Alfred Newerla 2021年9月7日上午6:01 #

感谢这篇精彩的教程。
请纠正代码段中的文件名以读取CSV文件
series = read_csv(‘daily-minimum-temperatures.csv’, header=0, index_col=0)
或重命名CSV文件本身（目前为：daily-min-temperatures.csv），以使文件名保持一致，从而避免Python找不到文件。
下载并放入工作目录后，我花了一点时间才弄明白为什么Python找不到文件。
谢谢。

回复
- Adrian Tam 2021年9月7日上午6:28 #
  
  好发现。谢谢！
  
  回复
sam 2021年11月10日上午1:03 #

你好，
我想获取这个模型的权重。但是model.weights不适用于这个特定模型。您能告诉我获取这个模型权重的方法吗？

回复
- Adrian Tam 2021年11月14日下午1:22 #
  
  模型中没有权重，但有系数。请看这一行：“print(‘Coefficients: %s’ % model_fit.params)”
  
  回复
Enes ince 2021年12月23日上午8:53 #

嘿！首先，感谢您的文章和指南，它们真的帮了我很多。

我的问题是，我们在这里构建了一个模型，我们的预测看起来非常好。但您能解释一下这种步进式（walk forward）方法是如何工作的吗？我将写下我的理解，请告诉我是否正确。

我们首先拟合模型并获得系数。我们有一个大小为窗口的训练数据集合，它位于训练数据的末尾，称为历史数据。之后，我们开始一个针对测试集大小的循环，在该循环中，我们获取滞后集，它最初是历史集，然后我们手动预测，我不明白为什么我们不直接使用forecast()函数，但无论如何我们这样做了，并且我们将预测值的原始值添加到训练集并继续，所以我们只用最后29个数据进行预测，并没有改变我们的模型。我希望它是这样工作的。

我不明白的是这有什么意义？我们不改变模型，我们不再重新拟合，这有什么意义？我们一直使用相同的系数。这只是表明我们的模型训练得有多好，并且它每次只预测1个值。为什么我们不直接去预测接下来的7个数据而不是这样做呢？

回复
- James Carmichael 2022年1月20日上午8:50 #
  
  嗨，Enes…关于您关于步进式验证的问题，请参阅以下内容：
  
  https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
  
  回复
Pablo 2022年3月13日上午6:09 #

嗨，谨以此表达我对这篇文章的感谢。祝好。

Pablo

回复
- James Carmichael 2022年3月13日下午1:09 #
  
  很棒的反馈，Pablo！
  
  回复
Pablo 2022年3月13日上午11:04 #

一个问题。

在持久性模型中，为什么您要定义函数model_persistence(x)？它除了返回相同的值之外什么也不做？您可以绘制test_X和test_y，它们会是相同的图吗？它只是为了表示/解释吗？

回复
- James Carmichael 2022年3月13日下午1:20 #
  
  嗨，Pablo…您说得对。它仅用于说明目的。
  
  回复
Stellah 2022年4月20日上午11:40 #

您好，Jason，再次感谢您的精彩指导。在另一种使用学习到的系数手动进行预测的情况下，如何修改代码来测试样本外数据？

回复
Sophia 2022年6月26日上午12:55 #

嗨，Jason，

感谢您的文章。

您代码中的片段
model = AutoReg(train, lags=29)
model_fit = model.fit()

您是如何确定滞后值为29的？
有什么方法可以让Statsmodels确定最佳滞后数吗？
您可以添加model_fit.aic来评估模型。

回复
- James Carmichael 2022年6月26日下午12:14 #
  
  嗨，Sophia…您可能需要研究超参数优化技术。
  
  https://machinelearning.org.cn/combined-algorithm-selection-and-hyperparameter-optimization/
  
  回复
GABZACHEW 2022年9月7日上午12:27 #

嗨，JASON
我有六个变量来预测用水量。
ID，月消费量，年份，客户类型，人口。
我的问题是如何使用回归模型编写自变量和因变量？

回复
Isadora 2022年11月9日上午11:44 #

嗨 James，

非常感谢，非常有帮助。

所以，如果我理解正确，您所说的“滚动AR模型”仅在测试集上进行滚动验证，但您的训练集只有一个，对吗？

您认为在滚动训练窗口中进行拟合怎么样？您有没有相关的代码示例？

再次感谢！

回复
- James Carmichael 2022年11月10日上午7:34 #
  
  嗨，Isadora…非常欢迎！您对“滚动AR模型”的理解是正确的！
  
  以下资源提供了许多代码示例，将有助于您更清楚地理解。
  
  https://machinelearning.org.cn/introduction-to-time-series-forecasting-with-python/
  
  回复
Izzy 2023年1月30日上午5:48 #

你好，

有没有办法获取静态和动态AR预测的标准误差？就像R中AR模型的predict函数有一个“prediction”元素和一个“standard error”元素，这样你就可以将置信区间与预测一起绘制出来。

到目前为止，这非常有帮助，谢谢。

回复
- James Carmichael 2023年1月30日上午9:38 #
  
  嗨，Izzy…以下资源中的一些想法可能会让您感兴趣：
  
  https://www.geeksforgeeks.org/how-to-plot-a-confidence-interval-in-python/
  
  回复
Amir 2023年4月24日上午3:43 #

嗨，Jason，

你是如何得出lag=29的？

回复
- James Carmichael 2023年4月24日上午8:57 #
  
  嗨，Amir…以下资源提供了另一种选择“滞后”的示例：
  
  https://towardsdatascience.com/how-to-use-an-autoregressive-ar-model-for-time-series-analysis-bb12b7831024
  
  回复
Jeremy 2023年12月18日上午7:26 #

Jason，这一切都非常有帮助！我很好奇为什么使用学习到的系数进行预测会提供比初始自回归预测（RMSE 1.225）稍接近的结果（RMSE 1.204）。在进行这类分析时，这是正常的预期行为吗？

回复
- James Carmichael 2023年12月18日上午8:07 #
  
  嗨，Jeremy…感谢您的反馈！由于这类模型是随机的，预计会出现差异。
  
  https://machinelearning.org.cn/stochastic-optimization-for-machine-learning/
  
  回复
Reza 2024年3月27日下午11:28 #

嗨，Jason，非常感谢您的有用课程。在实现AutoReg模型时，我发现相同的输入数据会得到不同的估计值。您知道原因吗？非常感谢。

回复
- James Carmichael 2024年3月28日上午2:34 #
  
  嗨，Reza…此资源可能会为您提供清晰的解释。
  
  https://machinelearning.org.cn/stochastic-in-machine-learning/
  
  回复
Reza 2024年3月28日下午1:14 #

嗨，Jason，非常感谢您提供的链接。根据维基百科，估计AR模型参数有两种一般方法：1）Yule-Walker方程和2）MLE。我熟悉MLE方法，其中参数是根据输入数据（随机）估计的。我的意思是，参数估计过程中没有随机数生成（随机性），您在提供的链接中清楚地解释了这一点。根据MLE方法，我期望如果我将相同的数据输入到AR模型中（训练数据、测试数据和AR的阶数），那么我将得到相同的估计值。我多次运行具有相同数据的AR，并获得了不同的估计值。我不确定估计过程是否使用了随机性（例如从正态分布生成随机数）。抱歉写得太长。

回复
- Reza 2024年3月28日下午1:21 #
  
  抱歉，在MLE方法中，我们根据给定的概率分布和观测数据来估计AR参数。我没有设置任何统计分布作为输入。第二次的观测数据（训练数据、测试数据和AR的阶数）是相同的，但我得到了不同的结果。
  
  回复
Walter Ohagwu 2024年4月9日上午5:09 #

感谢您的教程。不过，我想知道如何使用表达式 yhat = b0 + b1*X1 + b2*X2 … bn*Xn 手动实现预测（yhat）值。

回复
- James Carmichael 2024年4月9日上午7:23 #
  
  嗨，Walter…要在统计软件或编程环境中从自回归（AR）模型中检索回归系数，您可以使用您所用库提供的内置函数和方法。以下是如何使用`statsmodels`库（它是统计建模和计量经济学中常用的库）在Python中执行此操作的分步指南：
  
  ### 使用 Python 和 `statsmodels`
  
  1. **安装并导入必要的库**
  
  首先，请确保您已安装必要的库（`numpy`、`pandas`、`matplotlib`和`statsmodels`）。如果尚未安装，可以使用`pip`进行安装：
  
  bash pip install numpy pandas matplotlib statsmodels
  
  然后，在您的Python脚本或笔记本中导入这些库：
  
  python import numpy as np import pandas as pd import matplotlib.pyplot as plt from statsmodels.tsa.ar_model import AutoReg
  
  2. **准备时间序列数据**
  
  您需要一个时间序列数据集。这里，我将创建一个简单的模拟时间序列数据用于演示：
  
  python # 生成一些时间序列数据（例如，随机游走） np.random.seed(0) data = pd.Series(50 + np.random.normal(0, 1, 100).cumsum())
  
  3. **拟合自回归模型**
  
  根据领域知识选择适当的滞后数量，或使用ACF/PACF图等统计方法确定。在本例中，我假设我们选择一个滞后：
  
  python # 拟合AR模型 model = AutoReg(data, lags=1) fitted_model = model.fit()
  
  4. **检索并显示系数**
  
  拟合的模型对象包含估计的系数，其中包括截距（如果有）和滞后系数：
  
  python # 显示模型的回归系数 print("Coefficients of the model:") print(fitted_model.params)
  
  这将打印系数，包括常数项（截距）和模型中使用的每个滞后的系数。
  
  5. **使用系数进行进一步分析**
  
  这些系数可用于理解过去值对序列当前值的影响，或用于进行预测。以下是如何使用这些系数进行预测：
  
  python # 进行预测 predictions = fitted_model.predict(start=len(data), end=len(data) + 5, dynamic=False)
  # 绘制原始数据和预测值 plt.figure(figsize=(10, 5)) plt.plot(data, label='Original Data') plt.plot(np.arange(len(data), len(data) + 6), predictions, label='Forecast', linestyle='--') plt.legend() plt.show()
  
  ### 额外提示
  
  – **选择滞后数量**：AR模型中滞后的选择至关重要。滞后过少可能无法捕捉动态，而滞后过多可能导致过拟合。考虑使用AIC或BIC等统计标准进行选择。
  – **检查模型假设**：在拟合AR模型之前，务必检查时间序列数据的平稳性。非平稳数据可能导致虚假结果。
  
  通过遵循这些步骤，您可以有效地拟合AR模型，检索其系数，并将其用于预测或分析。这种方法可以根据需要适应更复杂的模型或不同类型的数据。
  
  回复

导航

使用 Python 进行时间序列预测的自回归模型

自回归

停止以慢速学习时间序列预测！

自相关

日最低气温数据集

快速检查自相关性

自相关图

持久性模型

自回归模型

进一步阅读

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入
您自己的项目

关于此主题的更多信息

221 条评论：使用 Python 进行时间序列预测的自回归模型

发表回复点击此处取消回复。

导航

自回归

停止以**慢速**学习时间序列预测！

自相关

日最低气温数据集

快速检查自相关性

自相关图

持久性模型

自回归模型

进一步阅读

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入您自己的项目

关于此主题的更多信息

221 条评论：使用 Python 进行时间序列预测的自回归模型

发表回复 点击此处取消回复。

停止以慢速学习时间序列预测！

最终将时间序列预测带入
您自己的项目

发表回复点击此处取消回复。