自然语言处理任务,如字幕生成和机器翻译,涉及生成单词序列。
针对这些问题开发的模型通常通过在输出单词词汇表上生成概率分布来工作,然后由解码算法对概率分布进行采样以生成最可能的单词序列。
在本教程中,您将了解可用于文本生成问题的贪婪搜索和束搜索解码算法。
完成本教程后,您将了解:
- 解码文本生成问题的方法。
- 贪婪搜索解码算法及其在Python中的实现方法。
- 束搜索解码算法及其在Python中的实现方法。
启动您的项目,阅读我的新书《自然语言处理深度学习》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2020年5月更新:修复了束搜索实现中的错误(感谢所有指出问题的人,以及Constantin Weisser提供的清晰修复)

如何为自然语言处理实现束搜索解码器
照片由See1,Do1,Teach1拍摄,保留部分权利。
文本生成解码器
在字幕生成、文本摘要和机器翻译等自然语言处理任务中,所需的预测是单词序列。
针对这些问题开发的模型通常会为输出序列中的每个单词在词汇表中的每个单词上输出一个概率分布。然后,解码过程将这些概率转换为最终的单词序列。
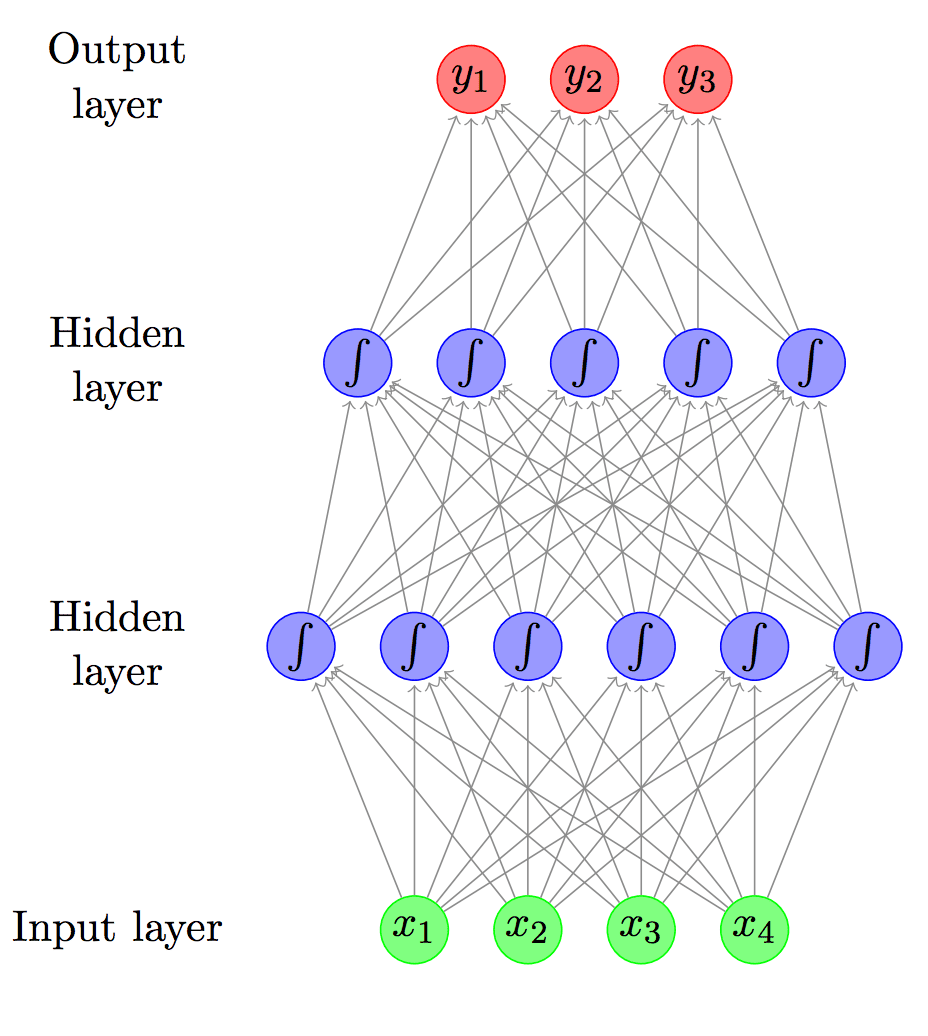
当您在自然语言处理任务中使用循环神经网络进行文本生成时,很可能会遇到这种情况。神经网络模型的最后一层有对应输出词汇表中每个单词的一个神经元,并使用softmax激活函数来输出词汇表中每个单词作为序列中下一个单词的可能性。
解码最可能的输出序列涉及根据其可能性搜索所有可能的输出序列。词汇表的大小通常是数万到数十万个单词,甚至数百万个单词。因此,搜索问题随着输出序列长度呈指数级增长,并且完全搜索是难以处理的(NP完全问题)。
在实践中,通常使用启发式搜索方法来为给定的预测返回一个或多个近似的或“足够好”的解码输出序列。
由于搜索图的大小是源句子长度的指数级,我们必须使用近似值来高效地找到解决方案。
— 第272页,《自然语言处理与机器翻译手册》,2011年。
候选单词序列根据其可能性进行评分。通常使用贪婪搜索或束搜索来定位文本候选序列。本文将介绍这两种解码算法。
每个单独的预测都有一个相关的分数(或概率),我们感兴趣的是分数最大(或概率最大)的输出序列……一种流行的近似技术是使用贪婪预测,在每个阶段选择得分最高的项目。虽然这种方法通常很有效,但它显然不是最优的。事实上,使用束搜索作为近似搜索通常比贪婪方法效果更好。
— 第227页,《自然语言处理中的神经网络方法》,2017年。
需要深度学习处理文本数据的帮助吗?
立即参加我的免费7天电子邮件速成课程(附代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
贪婪搜索解码器
一个简单的近似方法是使用贪婪搜索,在输出序列的每个步骤中选择最可能的单词。
这种方法的优点是速度很快,但最终输出序列的质量可能远非最优。
我们可以用一个小的、人为的Python示例来演示贪婪搜索的解码方法。
我们可以从一个涉及10个单词序列的预测问题开始。每个单词都以5个单词词汇表上的概率分布进行预测。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 定义一个在5个单词词汇表上的10个单词序列 data = [[0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1]] data = array(data) |
我们将假设单词已进行整数编码,因此列索引可用于查找词汇表中对应的单词。因此,解码任务就变成了从概率分布中选择一个整数序列的任务。
argmax()数学函数可用于选择具有最大值的数组的索引。我们可以使用此函数在序列的每个步骤中选择最有可能的单词索引。此函数直接在numpy中提供。
下面的greedy_decoder()函数使用argmax函数实现此解码器策略。
|
1 2 3 4 |
# 贪婪解码器 def greedy_decoder(data): # 每行的最大概率索引 return [argmax(s) for s in data] |
将所有内容放在一起,演示贪婪解码器的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
from numpy import array from numpy import argmax # 贪婪解码器 def greedy_decoder(data): # 每行的最大概率索引 return [argmax(s) for s in data] # 定义一个在5个单词词汇表上的10个单词序列 data = [[0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1]] data = array(data) # 解码序列 result = greedy_decoder(data) print(result) |
运行该示例将输出一个整数序列,然后可以将其映射回词汇表中的单词。
|
1 |
[4, 0, 4, 0, 4, 0, 4, 0, 4, 0] |
束搜索解码器
另一个流行的启发式方法是束搜索,它扩展了贪婪搜索并返回最可能的输出序列列表。
在构建序列时,束搜索不是贪婪地选择最可能的下一步,而是扩展所有可能的下一步,并保留k个最可能的,其中k是用户指定的参数,控制着通过概率序列的束或并行搜索的数量。
局部束搜索算法跟踪k个状态而不是一个。它从k个随机生成的状态开始。在每一步,生成所有k个状态的所有后继。如果其中任何一个是目标,算法就会停止。否则,它从完整列表中选择k个最佳后继并重复。
— 第125-126页,《人工智能:一种现代方法(第3版)》,2009年。
我们不需要从随机状态开始;相反,我们从k个最可能的单词开始作为序列的第一步。
常见的束宽度值为1表示贪婪搜索,而对于机器翻译的常见基准问题,值为5或10。更大的束宽度可以提高模型的性能,因为多个候选序列增加了更好匹配目标序列的可能性。这种性能的提高会导致解码速度下降。
在NMT中,新句子由简单的束搜索解码器翻译,该解码器查找能够近似最大化训练的NMT模型的条件概率的翻译。束搜索策略逐字从左到右生成翻译,同时在每个时间步保留固定数量(束)的活动候选。通过增加束的大小,翻译性能可以提高,但会显著降低解码速度。
— 神经机器翻译的束搜索策略,2017年。
搜索过程可以分别针对每个候选停止,方法是达到最大长度、达到序列结束标记或达到阈值可能性。
让我们用一个例子来具体说明。
我们可以定义一个函数来对给定的概率序列和束宽度参数k执行束搜索。在每一步,每个候选序列都用所有可能的下一步进行扩展。每个候选步骤通过将概率相乘来评分。选择k个概率最高的序列,并修剪所有其他候选。然后重复该过程直到序列结束。
概率是小数字,将小数字相乘会产生非常小的数字。为了避免浮点数下溢,将概率的自然对数加在一起,这使得数字更大且易于管理。此外,通过最小化分数来进行搜索也很常见。这个最后的调整意味着我们可以按分数升序对所有候选序列进行排序,并选择前k个作为最可能的候选序列。
下面的beam_search_decoder()函数实现了束搜索解码器。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 束搜索 def beam_search_decoder(data, k): sequences = [[list(), 0.0]] # 遍历序列中的每个步骤 for row in data: all_candidates = list() # 扩展每个当前候选 for i in range(len(sequences)): seq, score = sequences[i] for j in range(len(row)): candidate = [seq + [j], score - log(row[j])] all_candidates.append(candidate) # 按分数对所有候选进行排序 ordered = sorted(all_candidates, key=lambda tup:tup[1]) # 选择k个最佳 sequences = ordered[:k] return sequences |
我们可以将此与上一节的示例数据结合起来,这次返回3个最可能的序列。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
from math import log from numpy import array from numpy import argmax # 束搜索 def beam_search_decoder(data, k): sequences = [[list(), 0.0]] # 遍历序列中的每个步骤 for row in data: all_candidates = list() # 扩展每个当前候选 for i in range(len(sequences)): seq, score = sequences[i] for j in range(len(row)): candidate = [seq + [j], score - log(row[j])] all_candidates.append(candidate) # 按分数对所有候选进行排序 ordered = sorted(all_candidates, key=lambda tup:tup[1]) # 选择k个最佳 sequences = ordered[:k] return sequences # 定义一个在5个单词词汇表上的10个单词序列 data = [[0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1], [0.1, 0.2, 0.3, 0.4, 0.5], [0.5, 0.4, 0.3, 0.2, 0.1]] data = array(data) # 解码序列 result = beam_search_decoder(data, 3) # 打印结果 for seq in result: print(seq) |
运行该示例将同时打印整数序列及其对数似然。
尝试不同的k值。
|
1 2 3 |
[[4, 0, 4, 0, 4, 0, 4, 0, 4, 0], 6.931471805599453] [[4, 0, 4, 0, 4, 0, 4, 0, 4, 1], 7.154615356913663] [[4, 0, 4, 0, 4, 0, 4, 0, 3, 0], 7.154615356913663] |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
- 维基百科上的Argmax
- Numpy argmax API
- 维基百科上的束搜索
- 神经机器翻译的束搜索策略, 2017.
- 人工智能:一种现代方法(第3版), 2009.
- 自然语言处理中的神经网络方法, 2017.
- 自然语言处理与机器翻译手册, 2011.
- Pharaoh:一种用于短语统计机器翻译模型的束搜索解码器, 2004.
总结
在本教程中,您了解了可用于文本生成问题的贪婪搜索和束搜索解码算法。
具体来说,你学到了:
- 解码文本生成问题的方法。
- 贪婪搜索解码算法及其在Python中的实现方法。
- 束搜索解码算法及其在Python中的实现方法。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






这个Python/numpy示例非常具有误导性。它本质上假设单词的生成是完全独立的,或者换句话说——P(w_{t}|seq_{1:t-1}) = P(w_{t})。
在这种情况下,贪婪搜索的结果将*总是*与束搜索的最佳结果相同。
我建议修改
score = best_score[“i prev”] + -log P(word[i]|next)为——
score = best_score[“i prev”] +-log P(next|prev) + -log P(word[i]|next)并附上一个真实的RNN解码示例
谢谢,Noam。
我也觉得这有点令人困惑。我正在试图理解为什么你不会总是选择束搜索的第一个候选(即,只进行贪婪搜索,因为它更快)。
或者也许有其他方法可以确定那个不是最佳贪婪搜索得分的候选实际上是最佳候选?
我需要仔细考虑一下@Noam的建议。
抱歉,我的意思是
或者也许有其他方法可以确定那个不是最佳束搜索得分的候选实际上是最佳候选?
思路是通过概率序列搜索n个最佳路径。
这在Transformer模型中有多接近?
所以Noam,根据你的评论,-log P(next|prev)表示下一个字符在给定前一个字符的概率的负对数,对吗?例如,假设你预测一个单词的字符,并且预测出一个“r”。这个“r”之后的下一个前3个预测是“r”、“a”和“t”。现在,我们有P(next|'r'),最可能的是P('r'|'r')和P('t'|'r')都会很小,这样束搜索就能正确地选择P('a'|'r')并在我们的“r”之后输出“a”,对吗?
完全同意你的观点。我知道一个简单的例子有助于理解,但像这样的过度简化的例子只会误导读者。
所以不是我一个人这样想😀
我之前也对此感到困惑,因为我发现k>1的束搜索仍然会与贪婪搜索的结果相同。
Noam,能否通过给定的概率分布计算P(next|prev)?我正在尝试在编码器-解码器架构中实现束搜索,但我认为如果没有修改解码器,这是不可能的。
抱歉,我刚看到。我不确定实现方法,但思路是您不仅保存最后发出的单词,还保存状态(k个状态序列副本)。状态本身嵌入了P(next|prev),因此,例如,从w_{k-1}状态预测w_k,与从w_{k-1}状态的一个次优候选状态预测w_k是不同的。
请参阅https://www.youtube.com/watch?v=RLWuzLLSIgw
获取更多信息
先生,
您能给我一些机器学习研究工作的建议吗?
我需要机器学习中的问题或特定的研究趋势,
此致
Catherine。
抱歉,我无法帮助您进行研究课题。
如何将Beam Search与ARPA语言模型结合使用?
ARPA是什么?
ARPA是一种用于表示文本语料库中所有可能单词序列的格式。ARPA文件列出了每个可能的单词序列及其统计上估计的语言概率。
以下链接详细描述了ARPA格式
https://cmusphinx.github.io/wiki/arpaformat/
我想知道ARPA文件是否可用于从束搜索的输出中选择最佳序列?
谢谢。
可能有用。我不太了解。
先生,是否有其他启发式或元启发式搜索算法可以替代束搜索解码器??
当然,您可以使用其他搜索策略。
我不确定为什么示例会乘以对数概率。对数概率不是通常相加来得到乘以实值标量概率的等价物吗?
0.5 * 0.5 * 0.25 = 0.0625
log(0.5) + log(0.5) + log(0.25) = -2.772588722239781
exp(-2.772588722239781) == 0.0624
而
log(0.5) * log(0.5) * log(0.25) = -0.6660493039778589
exp(-0.6660493039778589) =~ 0.51374 != 0.625 ??
我认为Philip Glau是正确的。我们应该相加对数概率,而不是相乘。
代码的另一个问题是这行
” for j in range(len(row))”
您正在遍历行中的所有数据。在典型的文本生成问题中,词汇表中有很多单词,我们可能不想遍历所有单词?相反,我们应该只关心前k个概率。
+1 支持 Phillip 的评论。
另一个问题是log(1) = 0,所以任何包含概率接近1.0的字符的序列的 prod( log(p_i) ) ~ 0。
最终,这会导致推理过程中出现病态的解决方案退化。在我的结果中,它表现为长串的换行符。
Phillps 的数学计算是正确的。但是,如果你手动计算一个示例文子 logits,例如 [[1,2,3],[2,1,3],[3,1,2]],你会得到正确答案,它是 score*log(prob.) 而不是 score+log(prob.)。当我说是正确答案时,意味着 beam search 的最佳得分路径与 greedy 相同。上述 logits 的手动计算得出解码序列为 [2,2,0] (得分=27)、[2,0,0] (得分=18)、[1,2,0] (得分=18)。你可以通过 score*log 公式得到这些结果。另外请注意,无论你使用概率分布还是 logits 进行计算,答案都不应该改变。
对我上面的评论进行更正:为了最大化 log prob,你将 score 设置为 0,然后计算 score+log(prob)。在排序时,在 sorted() 中设置 reverse=True。这样,它就会给出我的第一个评论中的答案。
改进后的 beam search 实现
Phillips 的评论 +1 确实是错误的。概率相乘等同于对数概率相加。
谢谢 Ian。
可能需要修复文本,对于那些不阅读所有评论的人:“因此,概率的负对数相乘”
如果数据数组中的一个概率为零,应该怎么办?由于 log(0) 会出现数学错误。
好问题,在计算对数之前,可以给该值添加一个小的浮点数,例如 1e-9。
布朗利博士您好,
我正在尝试用不同的数据来做这个。
出于某种原因,我得到几乎相同的字幕,概率为 -0.0?
有什么建议吗?我将它与你的字幕生成器中的推理部分结合起来 https://machinelearning.org.cn/develop-a-deep-learning-caption-generation-model-in-python/
布朗利博士您好,
更高的对数似然性不是更好吗?如果是这样,那是否意味着在这个例子中第三个排序的序列是最好的?因为它具有最高的对数似然性?
[[4, 0, 4, 0, 4, 0, 4, 0, 4, 0], 0.025600863289563108]
[[4, 0, 4, 0, 4, 0, 4, 0, 4, 1], 0.03384250043584397]
[[4, 0, 4, 0, 4, 0, 4, 0, 3, 0], 0.03384250043584397]
为什么顺序是反的?
问题:为什么你要将对数相乘而不是相加,因为对数的相关性质是两个数的乘积可以等同于将它们的对数相加?
刚看到这个问题已经回答过了;我可能是累了。
谢谢。你能推荐一个 Keras seq2seq beam search 编码示例吗?会非常有帮助。
没有,抱歉,我没有示例。
亲爱的 Jason,
非常感谢您的教程。
我正在做一个 PyTorch 的聊天机器人系统,我想实现 beam_search 策略。
在验证和测试期间,我使用批次大小为 1,所以我的系统一次只看到一个序列。
我有一个编码器,它接收源序列,将其编码为上下文向量并返回其内部状态。这些状态用于初始化解码器的内部状态。解码器的第一个词是我的开始序列标记。
在循环给定最大长度后,解码器返回一些结果,这些结果通过一个 Dense 层,然后通过 log_softmax 操作,得到我的预测。
现在,假设我有一个最大长度为 10 个单词,一个小词汇量为 50 个单词,结果我得到:[10, batch size, 50]。
我可以将 [10, 50] 传给你的函数,然后检索最佳候选吗?也就是说,系统只对源序列运行一次,然后我们只搜索它的结果?
通常是的。具体来说,也许试试看?
我认为应该写“概率的自然对数加在一起”。对数概率相加等同于概率相乘。
Brownlee 博士您好。我发现在没有存储 t-1 步的隐藏状态用于 t 步的情况下,RNN 解码器将不会生成正确的序列。这是我的 CNN-LSTM 模型用于图像字幕任务的 beam search 解码器实现。 https://colab.research.google.com/drive/1-XV3yQhhslY144A5RHJrfWqILOv2iipv?authuser=2#scrollTo=eKtn21uj_K1z&line=7&uniqifier=1
干得好。
嗨 Jason,这篇文章非常有启发性。我想问除了 greedy 和 beam search 之外,还可以使用哪些其他启发式算法?
谢谢
谢谢。
好问题,也许可以查阅一下文献。
你能用这样的例子解释一下轨迹 beam search 吗?
感谢您的建议。
嗨,Jason,
我认为 beam_search_decoder 有更好的实现方式。
考虑我们讨论的是从机器翻译模型输出解码,其中输入数据是 n * m,n 是 MT 模型生成的词数,m 是目标语言词汇表的词数。
你的算法需要 O(n m k + n m log(m)),由于 m 会非常大(例如 20,000 个词),我们可以说你的算法需要 O(n m log(m))。
下面是我的实现,它只需要 O(n m + n k^2 + n k log(k)),也就是 O(n m)。
此实现的输出与你的实现输出相同。
并且通过对 (100, 20000) 大小的随机生成输入和 k=3 的多次试验,此实现快了 15 倍以上。
想法是,你不需要每次都遍历每个目标类的分数/概率,而是只需要取 k 个最大的分数。
感谢分享。
嗨 Jason,
我读过的最简单易懂的 Beam search 教程。
第 15 行 candidate = [seq + [j], score – log(row[j])]。
由于 log A + Log B = Log (AB)
为什么我们是“score – log(row[j])]”而不是“score + log(row[j])”?
谢谢。
你好 Jason,
一如既往,非常有用。
我有一个关于 beam search 的问题。可以手动 beam search 吗?例如,知道输出应该是“thank you”,我们可以说出它的 beam score 吗?
谢谢
当然。就像以总和的对数似然性作为得分一样。