线性回归是一个预测数值量的经典模型。线性回归模型的参数可以使用最小二乘法过程或最大似然估计过程进行估计。最大似然估计是一个概率框架，用于自动查找最能描述观测数据的概率分布和参数。监督式 [...]

密度估计是估计来自问题域的观测样本的概率分布的问题。有许多解决密度估计的技术，尽管机器学习领域广泛使用的一种通用框架是最大似然估计。最大似然估计涉及定义一个似然函数来计算条件概率 [...]

交叉熵在机器学习中常被用作损失函数。交叉熵是信息论领域的一个度量，它建立在熵的基础上，并通常计算两个概率分布之间的差异。它与 KL 散度密切相关但有所不同，KL 散度计算两个概率分布之间的相对熵，而交叉熵 [...]

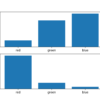
通常希望量化给定随机变量的概率分布之间的差异。这在机器学习中经常发生，因为我们可能对计算实际概率分布与观测概率分布之间的差异感兴趣。这可以通过信息论的技术来实现，例如 Kullback-Leibler 散度（KL 散度），或 [...]

信息增益计算通过某种方式转换数据集后，熵或惊喜的减少量。它通常用于通过评估每个变量的信息增益来构建决策树，并选择最大化信息增益的变量，这反过来又最小化熵并达到最佳 [...]

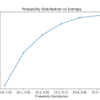
信息论是数学的一个子领域，关注通过有噪声信道传输数据。信息论的一个基石是量化消息中有多少信息。更普遍地说，这可用于量化事件和随机变量中的信息，称为熵，并且它计算 [...]

概率模型可以定义变量之间的关系并用于计算概率。例如，全条件模型可能需要大量的用于覆盖所有可能情况的数据，并且在实践中计算概率可能难以处理。诸如所有随机变量的条件独立性之类的简化假设可能有效，例如 [...]

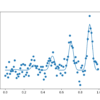
在本教程中，您将学习如何为复杂的优化问题实现贝叶斯优化算法。全局优化是一个具有挑战性的问题，即找到能使给定目标函数成本最小化或最大化的输入。通常，目标函数的形式很复杂且难以分析， [...]