神经网络是由相互连接的神经元节点组成。神经元不仅与相邻的神经元连接，还与较远的神经元连接。
神经网络的主要思想是，层中的每个神经元都有一个或多个输入值，它们通过对输入应用一些数学函数来产生输出值。一层中神经元的输出成为下一层神经元的输入。
单层神经网络是一种人工神经网络，其中输入层和输出层之间只有一个隐藏层。这是深度学习流行之前的经典架构。在本教程中，您将有机会构建一个只有单个隐藏层的神经网络。具体来说，您将学习
- 如何在 PyTorch 中构建单层神经网络。
- 如何使用 PyTorch 训练单层神经网络。
- 如何使用单层神经网络对一维数据进行分类。
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧。
在 PyTorch 中构建单层神经网络。
图片由 Tim Cheung 拍摄。部分权利保留。
概述
本教程分为三个部分；它们是
-
- 准备数据集
- 构建模型
- 训练模型
准备数据
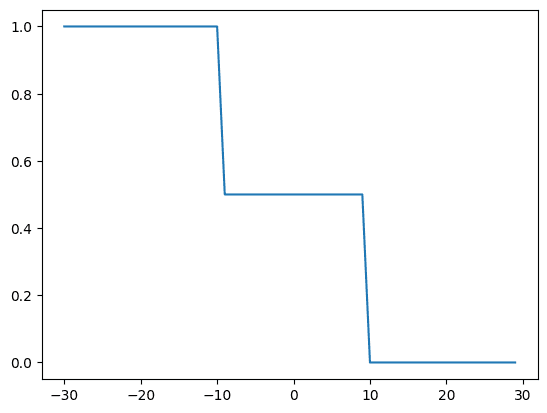
神经网络本质上是一个用某些参数来逼近其他函数的函数。让我们构建一些数据，看看我们的单层神经网络如何逼近函数，使其数据线性可分。稍后在本教程中，您将可视化训练过程中的函数，以查看逼近的函数如何与给定的一组数据点重叠。
|
1 2 3 4 5 6 7 8 9 |
import torch import matplotlib.pyplot as plt # 生成合成数据 X = torch.arange(-30, 30, 1).view(-1, 1).type(torch.FloatTensor) Y = torch.zeros(X.shape[0]) Y[(X[:, 0] <= -10)] = 1.0 Y[(X[:, 0] > -10) & (X[:, 0] < 10)] = 0.5 Y[(X[:, 0] > 10)] = 0 |
使用 matplotlib 绘制的数据如下所示。
|
1 2 3 |
... plt.plot(X, Y) plt.show() |
想开始使用PyTorch进行深度学习吗？
立即参加我的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
使用 nn.Module 构建模型
接下来，让我们使用 `nn.Module` 构建我们自定义的单层神经网络模块。如果您需要有关 `nn.Module` 的更多信息，请查看本系列的先前教程。
该神经网络具有一个输入层，一个具有两个神经元的隐藏层和一个输出层。在每个层之后，都会应用 sigmoid 激活函数。PyTorch 中有其他类型的激活函数，但此网络的经典设计是使用 sigmoid 函数。
这是您的单层神经网络在代码中的样子。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
... # 定义单层神经网络的类 class one_layer_net(torch.nn.Module): # 构造函数 def __init__(self, input_size, hidden_neurons, output_size): super(one_layer_net, self).__init__() # 隐藏层 self.linear_one = torch.nn.Linear(input_size, hidden_neurons) self.linear_two = torch.nn.Linear(hidden_neurons, output_size) # 定义层作为属性 self.layer_in = None self.act = None self.layer_out = None # 预测函数 def forward(self, x): self.layer_in = self.linear_one(x) self.act = torch.sigmoid(self.layer_in) self.layer_out = self.linear_two(self.act) y_pred = torch.sigmoid(self.linear_two(self.act)) return y_pred |
我们还可以实例化一个模型对象。
|
1 2 |
# 创建模型 model = one_layer_net(1, 2, 1) # 2 代表隐藏层中的两个神经元 |
训练模型
在开始训练循环之前，让我们为模型定义损失函数和优化器。您将为交叉熵损失编写一个损失函数，并使用随机梯度下降来优化参数。
|
1 2 3 4 |
def criterion(y_pred, y): out = -1 * torch.mean(y * torch.log(y_pred) + (1 - y) * torch.log(1 - y_pred)) return out optimizer = torch.optim.SGD(model.parameters(), lr=0.01) |
现在您拥有了训练模型的所有组件。让我们训练模型 5000 个 epoch。您将看到每 1000 个 epoch 后神经网络逼近函数的图。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 定义训练循环 epochs=5000 cost = [] total=0 for epoch in range(epochs): total=0 epoch = epoch + 1 for x, y in zip(X, Y): yhat = model(x) loss = criterion(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() # 获取总损失 total+=loss.item() cost.append(total) if epoch % 1000 == 0: print(str(epoch)+ " " + "个 epoch 完成!") # 每 1000 个 epoch 可视化结果 # 绘制函数逼近器的结果 plt.plot(X.numpy(), model(X).detach().numpy()) plt.plot(X.numpy(), Y.numpy(), 'm') plt.xlabel('x') plt.show() |
1000 个 epoch 后，模型逼近函数如下所示：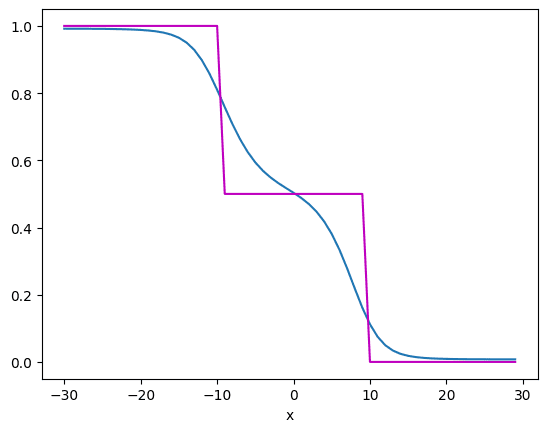
但在 5000 个 epoch 后，它改进为如下所示：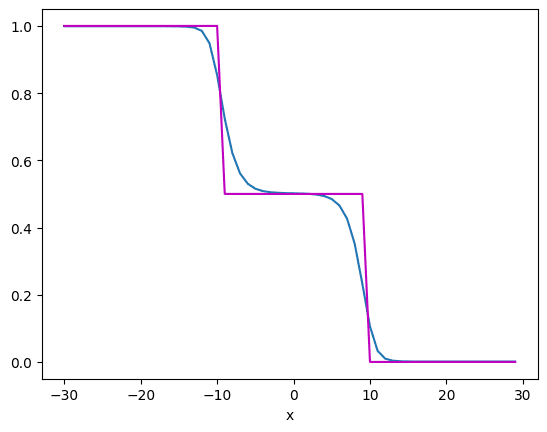
从中可以看到，蓝色曲线的逼近比紫色数据点更接近。正如您所见，神经网络对函数的逼近相当不错。如果函数更复杂，您可能需要更多的隐藏层或隐藏层中更多的神经元，即更复杂的模型。
我们还绘制图表以查看训练过程中损失的下降情况。
|
1 2 3 4 5 |
# 绘制成本 plt.plot(cost) plt.xlabel('epoch') plt.title('交叉熵损失') plt.show() |
您应该看到：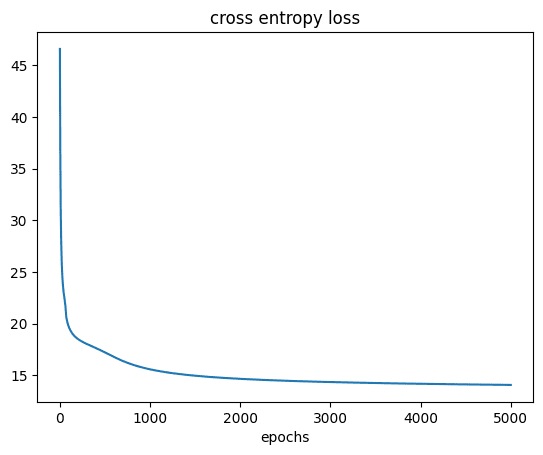
把所有东西放在一起，下面是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import torch import matplotlib.pyplot as plt # 生成合成数据 X = torch.arange(-30, 30, 1).view(-1, 1).type(torch.FloatTensor) Y = torch.zeros(X.shape[0]) Y[(X[:, 0] <= -10)] = 1.0 Y[(X[:, 0] > -10) & (X[:, 0] < 10)] = 0.5 Y[(X[:, 0] > 10)] = 0 plt.plot(X, Y) plt.show() # 定义单层神经网络的类 class one_layer_net(torch.nn.Module): # 构造函数 def __init__(self, input_size, hidden_neurons, output_size): super(one_layer_net, self).__init__() # 隐藏层 self.linear_one = torch.nn.Linear(input_size, hidden_neurons) self.linear_two = torch.nn.Linear(hidden_neurons, output_size) # 定义层作为属性 self.layer_in = None self.act = None self.layer_out = None # 预测函数 def forward(self, x): self.layer_in = self.linear_one(x) self.act = torch.sigmoid(self.layer_in) self.layer_out = self.linear_two(self.act) y_pred = torch.sigmoid(self.linear_two(self.act)) return y_pred # 创建模型 model = one_layer_net(1, 2, 1) # 2 代表隐藏层中的两个神经元 def criterion(y_pred, y): out = -1 * torch.mean(y * torch.log(y_pred) + (1 - y) * torch.log(1 - y_pred)) return out optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 定义训练循环 epochs=5000 cost = [] total=0 for epoch in range(epochs): total=0 epoch = epoch + 1 for x, y in zip(X, Y): yhat = model(x) loss = criterion(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() # 获取总损失 total+=loss.item() cost.append(total) if epoch % 1000 == 0: print(str(epoch)+ " " + "个 epoch 完成!") # 每 1000 个 epoch 可视化结果 # 绘制函数逼近器的结果 plt.plot(X.numpy(), model(X).detach().numpy()) plt.plot(X.numpy(), Y.numpy(), 'm') plt.xlabel('x') plt.show() # 绘制成本 plt.plot(cost) plt.xlabel('epoch') plt.title('交叉熵损失') plt.show() |
总结
在本教程中，您学习了如何构建和训练神经网络以及估计函数。特别是，您学会了
- 如何在 PyTorch 中构建单层神经网络。
- 如何使用 PyTorch 训练单层神经网络。
- 如何使用单层神经网络对一维数据进行分类。
开始使用PyTorch进行深度学习！
学习如何构建深度学习模型
...使用新发布的PyTorch 2.0库
在我的新电子书中探索如何实现
使用 PyTorch进行深度学习
它提供了包含数百个可用代码的自学教程，让你从新手变成专家。它将使你掌握：
张量操作、训练、评估、超参数优化等等...
我一直关注 Khan 先生的教程。
首先，它们写得很清楚，其次，他的教程的副产品是实例化类、从父类继承以及实现继承类的应用。
谢谢你，
悉尼的Anthony
你好，我跟着代码，使用了 jupyter notebook，运行良好。
epoch 计算需要时间。我如何将代码转换为使用 CUDA 运行，以加速速度？
你好 Alex.A…… 以下资源是一个很好的起点
https://www.vincent-lunot.com/post/an-introduction-to-cuda-in-python-part-1/