展示机器学习模型的预期技能以及该模型技能的置信区间都很重要。
置信区间提供了模型技能的范围,以及在对新数据进行预测时,模型技能落在该范围内的可能性。例如,分类准确率在70%到75%之间的可能性为95%。
计算机器学习算法置信区间的稳健方法是使用bootstrap。这是一种估计统计量的通用技术,可用于计算经验置信区间,而与技能分数(例如非高斯分布)的分布无关。
在本帖中,您将了解如何使用bootstrap来计算机器学习算法性能的置信区间。
阅读本文后,你将了解:
- 如何使用bootstrap估计统计量的置信区间。
- 如何应用此方法来评估机器学习算法。
- 如何在Python中实现bootstrap方法来估计置信区间。
通过我的新书《机器学习统计学》启动您的项目,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2017年6月更新:修复了向numpy.percentile()提供错误值的问题。感谢Elie Kawerk。
- 2018年3月更新:更新了数据集文件的链接。

如何在 Python 中为机器学习结果计算 Bootstrap 置信区间
照片由Hendrik Wieduwilt拍摄,保留部分权利。
Bootstrap置信区间
使用bootstrap计算置信区间包括两个步骤:
- 计算统计量总体
- 计算置信区间
需要机器学习统计学方面的帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
1. 计算统计量总体
第一步是使用bootstrap程序对原始数据进行多次重采样,并计算感兴趣的统计量。
数据集是带放回抽样的。这意味着每次从原始数据集中选择一个项目时,它都不会被移除,从而允许该项目可能被再次选中作为样本。
在样本上计算统计量并将其存储起来,以便我们建立感兴趣的统计量总体。
Bootstrap重复次数决定了估计量的方差,越多越好,通常是几百或几千次。
我们可以用以下伪代码演示此步骤。
|
1 2 3 4 5 |
statistics = [] for i in bootstraps sample = select_sample_with_replacement(data) stat = calculate_statistic(sample) statistics.append(stat) |
2. 计算置信区间
现在我们有了感兴趣的统计量总体,我们可以计算置信区间。
这首先是通过对统计量进行排序,然后选择置信区间所需百分位数的值来完成的。这里选择的百分位数称为alpha。
例如,如果我们对95%的置信区间感兴趣,那么alpha将是0.95,我们将选择2.5%百分位数的值作为下界,97.5%百分位数的值作为上界。
例如,如果我们从1000个bootstrap样本中计算出1000个统计量,那么假设统计量列表已排序,下界将是第25个值,上界将是第975个值。
在这里,我们计算的是非参数置信区间,它不对统计量分布的函数形式做任何假设。这个置信区间通常被称为经验置信区间。
我们可以用下面的伪代码来演示。
|
1 2 3 |
ordered = sort(statistics) lower = percentile(ordered, (1-alpha)/2) upper = percentile(ordered, alpha+((1-alpha)/2)) |
Bootstrap模型性能
Bootstrap可用于评估机器学习算法的性能。
每次迭代抽样的样本大小可能限制为可用数据的60%或80%。这意味着有些样本将不包含在样本中。这些被称为袋外(OOB)样本。
然后,可以在每次bootstrap迭代的数据样本上训练模型,并在袋外样本上进行评估,以获得性能统计量,这些统计量可以收集起来并从中计算置信区间。
我们可以用以下伪代码演示此过程。
|
1 2 3 4 5 6 |
statistics = [] for i in bootstraps train, test = select_sample_with_replacement(data, size) model = train_model(train) stat = evaluate_model(test) statistics.append(stat) |
计算分类准确率置信区间
本节将演示如何使用bootstrap,通过scikit-learn这个Python机器学习库,在真实数据集上为机器学习算法计算经验置信区间。
本节假设您已安装Pandas、NumPy和Matplotlib。如果您在设置环境方面需要帮助,请参阅教程。
首先,下载Pima Indians数据集,并将其放置在当前工作目录中,文件名为“pima–indians-diabetes.data.csv”(更新:可在此处下载)。
我们将使用Pandas加载数据集。
|
1 2 3 |
# 加载数据集 data = read_csv('pima-indians-diabetes.data.csv', header=None) values = data.values |
接下来,我们将配置bootstrap。我们将使用1000次bootstrap迭代,并选择数据集大小为50%的样本。
|
1 2 3 |
# 配置bootstrap n_iterations = 1000 n_size = int(len(data) * 0.50) |
接下来,我们将迭代bootstrap。
样本将使用sklearn的resample()函数进行带放回抽样。任何未包含在样本中的行将被检索并用作测试数据集。接下来,在样本上拟合决策树分类器,并在测试集上进行评估,计算分类分数,并将其添加到所有bootstrap中收集的分数列表中。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 运行bootstrap stats = list() for i in range(n_iterations): # 准备训练集和测试集 train = resample(values, n_samples=n_size) test = numpy.array([x for x in values if x.tolist() not in train.tolist()]) # 拟合模型 model = DecisionTreeClassifier() model.fit(train[:,:-1], train[:,-1]) # 评估模型 predictions = model.predict(test[:,:-1]) score = accuracy_score(test[:,-1], predictions) |
收集完分数后,将创建直方图以展示分数的分布情况。我们通常期望此分布呈高斯分布,可能带有均值周围对称方差的偏斜。
最后,我们可以使用NumPy的percentile()函数来计算经验置信区间。使用95%置信区间,因此选择2.5%和97.5%百分位数的值。
综上所述,完整的示例代码如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import numpy from pandas import read_csv from sklearn.utils import resample from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import accuracy_score from matplotlib import pyplot # 加载数据集 data = read_csv('pima-indians-diabetes.data.csv', header=None) values = data.values # 配置bootstrap n_iterations = 1000 n_size = int(len(data) * 0.50) # 运行bootstrap stats = list() for i in range(n_iterations): # 准备训练集和测试集 train = resample(values, n_samples=n_size) test = numpy.array([x for x in values if x.tolist() not in train.tolist()]) # 拟合模型 model = DecisionTreeClassifier() model.fit(train[:,:-1], train[:,-1]) # 评估模型 predictions = model.predict(test[:,:-1]) score = accuracy_score(test[:,-1], predictions) print(score) stats.append(score) # 绘制分数 pyplot.hist(stats) pyplot.show() # 置信区间 alpha = 0.95 p = ((1.0-alpha)/2.0) * 100 lower = max(0.0, numpy.percentile(stats, p)) p = (alpha+((1.0-alpha)/2.0)) * 100 upper = min(1.0, numpy.percentile(stats, p)) print('%.1f confidence interval %.1f%% and %.1f%%' % (alpha*100, lower*100, upper*100)) |
运行示例代码会为每次bootstrap迭代打印分类准确率。
创建了1000个准确率分数的直方图,显示了类似高斯分布的分布。
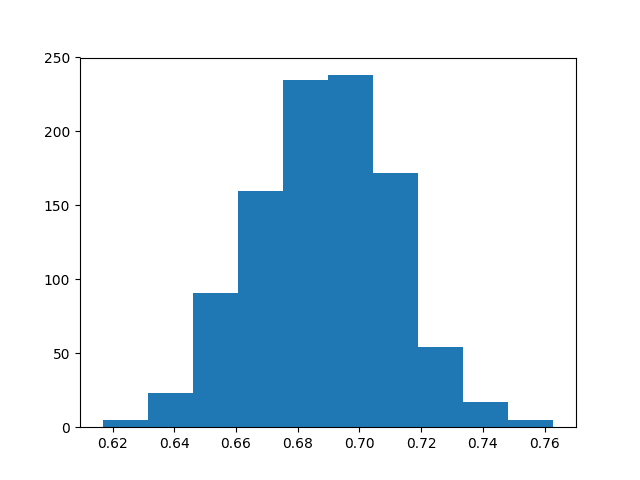
使用Bootstrap的分类准确率分布
最后,报告了置信区间,表明置信区间64.4%到73.0%覆盖模型真实技能的可能性为95%。
|
1 2 3 4 5 6 7 |
... 0.646288209607 0.682203389831 0.668085106383 0.673728813559 0.686021505376 95.0 置信区间 64.4% 和 73.0% |
同样的方法也可用于计算其他错误分数(如回归算法的均方根误差)的置信区间。
进一步阅读
本节提供有关bootstrap和bootstrap置信区间的附加资源。
- Bootstrap 导论, 1996
- Bootstrap置信区间,Statistical Science,1996
- 第5.2.3节,Bootstrap置信区间,人工智能经验方法
- Wikipedia上的Bootstrap
- 第4.4节重采样技术,应用预测建模
总结
在本帖中,您学习了如何使用bootstrap来计算机器学习算法的置信区间。
具体来说,你学到了:
- 如何计算来自数据集的统计量的置信区间的bootstrap估计。
- 如何应用bootstrap来评估机器学习算法。
- 如何在Python中为机器学习算法计算bootstrap置信区间。
您对置信区间有什么疑问吗?
请在下面的评论中提出您的问题。






谢谢你,Jason。
我很高兴您发现这篇文章有用。
在哪里可以买到您的书“Mastering machine learning with python”?
这里:
https://machinelearning.org.cn/machine-learning-with-python/
先生,我们如何将bootstrap重采样应用于软件工作量区间预测,以及需要遵循的程序和初始步骤是什么?
收集您的数据,在Python中加载它,并应用该程序来估计所需的量。
您在哪个部分遇到了困难?
谢谢你,Jason。
您是否考虑将关于置信区间的帖子包含在之前的(或新的)书中?
此致
Elie
嗨Elie,
不特别。我有一个关于“机器学习统计方法”的粗略想法,可能会涵盖抽样理论和置信区间等主题。像这样的帖子是测试人们是否有兴趣。
你为什么这么问?这是您正在寻求更多帮助的主题吗?
是的,
我发现像这样的帖子对报告统计上有意义的机器学习结果非常有用。这是一个关于该主题的很好的免费书籍链接:https://www.otexts.org/book/sfml
此致
Jason,
我还有个问题。如何在hold-out集上进行的评估中报告置信区间?您无法在此处应用训练的bootstrap,因为这会污染我们的结果。
此致
通常,您可以多次重复holdout过程,使用不同的随机样本,并将结果作为结果的总体。
我同意,这本不错的书!
通过从一个holdout集中以一定次数的迭代进行抽样而不进行任何训练,是否适合应用bootstrap?
就像只对用于评估模型技能的数据集进行重采样?
不,我认为这不合适。
Jason,
您获得的置信区间似乎有些不对。您计算的是[61.5, 63.9]。然而,我得到的平均值约为69%(与您从图中获得的相似),并且目测估计95% CI为[64, 74]。我认为有些地方不对。
如果我错了,请纠正我。
此致
Elie
Elie,你说得对,非常感谢。
提供给numpy.percentile()的值必须在[0,100]范围内,而我提供了[0,1]范围的值。
我已经修复了示例,并更清楚地说明了百分位数值的计算方式(以便我们应该有的怀疑论者开发者可以进行调试)。
我非常感谢您找到这个问题并发表评论。这使得示例对每个人都更好!
np.quantile(q) = np.percentile(p) for q=p/100
我喜欢这些关于机器学习的“小菜一碟”的笔记。
谢谢 Dawit。
嗨 Jason,感谢您的这篇文章。使用训练集拟合分类器,然后在看不见的数据(holdout集)上计算其准确率的概念是否已经过时?在我看来,CV测试的是您的算法(带优化参数)在构建模型方面的能力,因为模型在每个折叠中都会在测试其在hold-out折叠上的性能之前重新拟合。它似乎没有预测已训练模型在投入生产并开始对完全新的实例进行分类时会如何工作。为此,除了在完整训练集上训练并针对holdout集进行测试之外,我看不到其他选择——我是否遗漏了什么?
交叉验证(CV)在做同样的事情,只是重复了10次,对于10折CV。
CV和训练/测试拆分都是重采样方法,旨在估计模型在看不见的数据上的技能。也许这篇帖子会为您澄清一些问题。
https://machinelearning.org.cn/train-final-machine-learning-model/
在许多拥有数百万示例的问题(例如深度学习)中,我们通常没有资源进行CV。
感谢您提供的链接——这澄清了很多问题!总而言之,如果拥有执行它的处理能力和时间,k折验证是否总是更优的选择,因为它提供了均值、标准差和置信区间?
通常,CV会提供对模型技能的较低偏差估计。这是该方法的主要目标。
我经常使用bootstrap来展示选定配置的最终置信区间。
嗨,感谢您的文章。我正在尝试计算灵敏度和特异度的置信区间。我使用了您的代码,但更改了准备步骤,使用了“train_test_split”(带随机种子),来创建数据样本。然后在每次迭代中,我拟合了一个模型并进行了预测,然后创建了一个混淆矩阵,然后计算了灵敏度和特异度。您认为这合理吗?结果看起来是合理的。
谢谢。
我认为bootstrap方法也适用于其他准确率相关的度量。
好文章(
如果人们觉得懒惰,提及bootsrapped包可能有用;)
https://pypi.python.org/pypi/bootstrapped/0.0.1
感谢您提供的链接,Ian。
很棒的文章,Jason。我想知道您是否认为使用bootstrap方法对神经网络进行估计置信度是可行的?
当然!
我如何估计某个看不见的数据点的95%分类准确率?
假设我有了三个新的数据点 x1、x2、x3。我如何估计我的方法在预测 x2 时有 95% 的可能性分类准确率在 80% 到 85% 之间,但预测 x1 时在 60% 到 65% 之间,预测 x3 时在 90% 到 95% 之间?
听起来您可能是在询问预测区间,而不是置信区间。
我在我的统计学书中涵盖了这一点,并且很快就会有一篇关于该主题的文章。
在那之前,请看这篇文章
https://en.wikipedia.org/wiki/Prediction_interval
感谢链接!
尊敬的Jason博士,
虽然我理解上面提出的总体概念,但在一个细节上我有些困惑:
第 21 和 23 行。这是关于选择数组 [:,:-1] 和 [:,-1] 的。
这是关于
和
换句话说,当有一个数组时,选择方法之间有什么区别?
和
谢谢你,
悉尼的Anthony
是的,我们正在选择列。
您可以在此处了解有关数组切片的更多信息
https://machinelearning.org.cn/index-slice-reshape-numpy-arrays-machine-learning-python/
尊敬的Jason博士,
感谢您提供的参考。我承认我当时遇到了困难。今天我明白了。
此致
悉尼的Anthony
很高兴听到这个消息。
你好,
您能否为完整示例的第 32 行和第 34 行的表达式提供参考?框架?
p = ((1.0-alpha)/2.0) * 100
p = (alpha+((1.0-alpha)/2.0)) * 100
谢谢
也许看看文章末尾的参考文献。
请忽略我之前的评论。我刚刚注意到 alpha 设置为 .95。
现在它们说得通了。
不客气。
你好!非常感谢你的帖子!
但是我不理解你的置信区间。如果你想要 95% 的置信区间,难道不应该将 alpha 设置为 0.05 吗?
祝好,
Santiago
也许重新阅读一下这篇文章。请记住,我们想要两侧,例如均值两侧都有 2.5% 的间隔。
也许这会有帮助。
https://machinelearning.org.cn/confidence-intervals-for-machine-learning/
这非常直观。感谢您的写作
谢谢。
Jason,
感谢您写这篇文章!!
在我攻读物理学博士学位期间,我们必须将难以处理的(高度)非线性函数拟合到真实数据中,并且对我们(作为“新兴”科学家)来说,至少尝试报告我们结果的标准误差和系统误差是至关重要的。
在学习和使用整个学校的误差传播方法时,我惊讶地在学习后期才知道,bootstrap 方法是(合法的)首选方法,用于(模拟的)复杂函数参数的标准误差估计。
当各种尺度的自然构成部分似乎经常表现出非线性相互作用动力学时,人们会认为我们的工程师和科学教学先驱(例如,对于工程师、物理学家、化学家、生物学家等)应该强调该方法的价值和进一步研究,特别是在一个时代,现在人们的关注点更多地放在现象学研究上,而较少关注纯粹的分析理论。
最后,我仍然感谢 DS 和 ML 的进步,它们使这些现象学研究和基础预测分析能够被大众,尤其是像我这样的普通人所接触到。
再次感谢您又一篇精彩的文章!!
谢谢分享,我非常同意您的观点。
事实上,应该普遍教授更多的模拟/蒙特卡洛方法。
嗨,Jason,
关于这个主题的精彩文章。它极大地帮助了我。我一直在尝试将此应用于 AUC 的 CI,在可视化抽样分布后,它看起来像一个截断的正态分布。您在计算 CI 时是否处理过这类分布?任何建议都将不胜感激。
抱歉,我没有。
也许尝试将实验重复 100 多次,然后查看分布,例如直方图和可能的统计检验。
我觉得这篇文章非常有帮助。我一直在处理一个数据集,其中我使用 RandomForestRegressor 来预测 2 个输出(多输出),并且有 17 个预测变量。我制作了模型和预测,但我想要它们的预测区间,我阅读了关于 jackknife 和 infinitesimal jackknife 以及 quantile regression 的论文,并了解了 foresci 包,该包基于 jackknife 论文制作区间,但没有一篇解释了多输出案例,例如如何找到多变量情况的区间。如果您能给我一些建议,将会有所帮助。
谢谢您的建议,我将来可能会涵盖该主题。
嗨 Jason,非常感谢,我喜欢这篇文章,它超级有用和清晰。
我有一个问题:我现在只对置信区间感兴趣,我注意到改变样本量会给我不同的区间。我遇到了 Seaborn 包,它有一个 bootstrap 函数,它接受等于数据集大小 100% 的样本 [1]。
使用等于数据集 100% 的样本量进行抽样是否可以?为什么区间会变化?
感谢您能提供的任何指导。
[1] https://github.com/mwaskom/seaborn/blob/b9551aff1e2b020542a5fb610fec468b69b87c6e/seaborn/algorithms.py#L86
是的,我认为使用 100% 的 bootstrap 样本是一种标准做法。
你好!
这篇博文非常有帮助,非常感谢!
我想问一下:如果我们进行了不是 bootstrap,而是 shuffle split CV。并从中得到一系列指标值。我们可以测试这些值的正态性(例如使用 Shapiro 检验),如果未拒绝原假设,则构建一个未知标准差的均值置信区间(x.mean ± t\*s/sqrt(n))?我曾尝试这样做,但我对这些计算的正确性不太确定。
感谢您能提供的任何建议!
可能有点混乱,例如 m 次重复和不同分割的 k 个均值。
我不确定其含义,抱歉。也许咨询一下统计学家?
非常好的文章!你能建议一下如何将 Bootstrapping 与逻辑回归一起使用吗?我想在每次迭代中更改 C 值。这该如何实现?
谢谢!
听起来很简单,你具体遇到的问题是什么?
我不确定如何为逻辑回归发送一系列 C 值,以及哪个值会给我最好的解决方案。你能提供一下语法吗?目前我正在使用 LogReg.fit 来进行逻辑回归,但不确定如何分配不同的 C。另外,C 是否可以优化?
谢谢!
也许尝试在对数尺度上的一系列 C 值?
嗨,有没有什么理由你不使用替换?以及我们应该保留原始数据集的多少百分比用于每次 bootstrap?这只是随机的吗?
谢谢
bootstrap 使用替换。
bootstrap 大小应与原始数据集大小匹配,这是一个很好的经验法则。
谢谢
在重采样时,我们应该关心分层吗?
是的,可能。
谢谢 Jason!一如既往,精彩的文章。
mlxtend Python 包实现了很好的 bootstrap,以及 .632 和 .632+ 方法 (bootstrap_point632.py)。我唯一的抱怨是它目前一次只能接受一个评分函数,但我正在做一个 PR 来使其对多个分数更有效。🙂
感谢分享。
您好 Jason 博士,
这很棒。我想计算 H2o 的 XGBoost 的置信区间。我不太理解几个步骤。我将数据应用到 XGBoost,将其分为训练、验证和测试,假设是时间序列案例。我们如何将其放入迭代中?我很感谢您的指导。
import numpy
from pandas import read_csv
from sklearn.utils import resample
from sklearn.metrics import accuracy_score
from matplotlib import pyplot
from xgboost import XGBRegressor
# 加载数据集
#data = read_csv(‘pima-indians-diabetes.data.csv’, header=None)
#values = data.values
# 配置bootstrap
n_iterations = 100
n_size = int(len(hf_train) * 0.50)
# 运行bootstrap
stats = list()
for i in range(n_iterations)
# prepare train and test sets
#train = resample(values, n_samples=n_size)
#test = numpy.array([x for x in values if x.tolist() not in train.tolist()])
# 拟合模型
import h2o
from h2o.estimators.xgboost import H2OXGBoostEstimator
h2o.init()
param = {
“ntrees” : 10000
, “nfolds” : 0
,”stopping_rounds” : 40
, “max_depth” : 25
,”stopping_tolerance” : 0.005
, “learn_rate” : 0.05
, “eta” : 0.3
, “sample_rate” : 0.8
, “subsample” : 1
, “col_sample_rate” : 1
, “col_sample_rate_per_tree” : 1
, “colsample_bylevel” : 1
, “min_rows” : 0.06
,”min_child_weight”: 1
, “sample_type” : “uniform”
, “normalize_type” : “tree”
,”nthread” : -1
, “max_bins” : 256
, “max_leaves” : 0
, “seed”: 1601
, “score_tree_interval”: 0
,”reg_lambda” : 0.1
,”reg_alpha” : 1/1
,”grow_policy” : “depthwise”
, “booster” : “gbtree”
}
from h2o.estimators import H2OXGBoostEstimator
model = H2OXGBoostEstimator(**param)
model.train(x = X, y = y, training_frame = hf_train, validation_frame = hf_valid)
# 评估模型
predictions = model.predict(hf_test)
score = model.model_performance(test_data= hf_test)
print(score)
stats.append(score)
# 绘制分数
pyplot.hist(stats)
pyplot.show()
# 置信区间
alpha = 0.95
p = ((1.0-alpha)/2.0) * 100
lower = max(0.0, numpy.percentile(stats, p))
p = (alpha+((1.0-alpha)/2.0)) * 100
upper = min(1.0, numpy.percentile(stats, p))
print(‘%.1f confidence interval %.1f%% and %.1f%%’ % (alpha*100, lower*100, upper*100))
这是我在这里回答的一个常见问题
https://machinelearning.org.cn/faq/single-faq/can-you-read-review-or-debug-my-code
谢谢:有道理。
不客气。
Jason博士您好,
我遵循了上面链接中“将问题分解为小级别”的步骤。我现在已经成功地将其应用于 XGBoost H2o。我仍然需要您在几个方面的指导。
第一:我想将数据分为训练、验证和测试。模型使用训练数据进行训练,使用验证数据进行评分,并使用测试数据获得模型的最终分数。我们如何改变它?
train = resample(values, n_samples=n_size)
test = numpy.array([x for x in values if x.tolist() not in train.tolist()])
第二:我不明白为什么置信区间的下限和上限相同(即 4.4% 和 4.4%)。我正在为回归做。对于分数,我使用
score = model.rmse()
您可以使用此函数将数据分割成子集
https://scikit-learn.cn/stable/modules/generated/sklearn.model_selection.train_test_split.html
非常感谢:我已将第二个问题发布到 Stackoverflow,其中包含可重现的代码。
https://stackoverflow.com/questions/60956655/bootstrap-confidence-intervals-for-xgboost-h2o-regression-python
干得好。
Jason 博士:我仍在寻找我第二个问题(3月31日评论)的答案。
在您的示例中。当我们打印(score)时,我们会得到与 n_iterations 数量相同的分数。这就是我们可以绘制直方图的方式。
score = accuracy_score(test[:,-1], predictions)
print(score)
在我的情况下:XGBoost h2o。(所有代码都可以在 Stackoverflow 中看到)。当我执行 n_iterations 时,我得到一个单一的分数。这就是问题所在。我们该如何解决?
predictions = model.predict(test_hf1)
score = model.rmse()
print(score)
抱歉,我对 h20 API 不了解,不确定能否给您建议。也许联系他们的支持?
非常感谢您一直以来的及时回复。我已经联系了 H2O。我也在处理这个问题。
很高兴听到这个消息,祝你好运!
我用 LightGBM 库检查了一下,发现它在回归方面与 XGBoost H2o 存在同样的问题。在我看来,这些代码对回归不起作用。它在分类方面效果很好。这也意味着问题不在于特定的 API(如 H2o),而在于应用于回归或分类。它在分类方面工作正常。
如果您能为我检查一下回归,我将非常感谢您。
是的,代码示例计算的是准确率,您必须将其更改为像 MSE 这样的误差分数。
可能我没有解释清楚我的问题。我已经改为 MSE/RMSE,但问题没有解决。它只在分类情况下完美工作。
score = np.sqrt(mean_squared_error(yt, y_pred))
print(score)
stats.append(score)
# 绘制分数
pyplot.hist(stats)
pyplot.show()
# 置信区间
alpha = 0.95
p = ((1.0-alpha)/2.0) * 100
lower = max(0.0, numpy.percentile(stats, p))
p = (alpha+((1.0-alpha)/2.0)) * 100
upper = min(1.0, numpy.percentile(stats, p))
print(‘%.1f confidence interval %.1f%% and %.1f%%’ % (alpha*100, lower*100, upper*100))
听到这个消息我很难过,为什么不行?您具体遇到的问题是什么?
我现在已将问题发布到 https://github.com/dmlc/xgboost/issues/5475
尝试绘制数据以确认是否存在分布。可能不存在。
如果存在,请尝试更改直方图的 bin 数量。
是的,我也尝试过,但没有奏效
import seaborn as sns; sns.set()
sns.distplot(stats, hist=True, kde=False, bins=int(10), color = ‘blue’, hist_kws={‘edgecolor’:’black’})
打印预测值并查看它们,确保有一些分布。也许没有,在这种情况下一切都在正常工作。
非常感谢!我现在已经绘制了预测图,分布看起来很好。您可以在此处找到:https://github.com/dmlc/xgboost/issues/5475
不错。
每次运行都打印平均误差值怎么样?
我认为问题与当我们迭代进行自助法采样并使用 print(score) 时,可以获得与分类迭代次数一样多的分数次数有关,但对于回归,我们得不到,而是在迭代过程中只得到一个分数。但我不知道如何解决。
如果多次运行的平均性能没有变化,那可能不是错误。这意味着问题很简单,模型非常稳定。
当我使用 print(error) 时,我无法获得运行的平均误差。
error = np.mean(predictions-y_test)
使用 sklearn 库来计算它
https://scikit-learn.cn/stable/modules/generated/sklearn.metrics.mean_squared_error.html#sklearn.metrics.mean_squared_error
谢谢!:我已经用包括 sklearn 在内的各种方法做过了
score = mean_squared_error(y_test,y_pred, squared= True)
使用这个函数。
但什么都没用。有没有办法像您代码中的 rmse[i] 那样将 rmse 整合到循环中?虽然我自己也在尝试。
我在 R 中使用 XGBoost H2o 做到过。在少量迭代中效果很好。但我在大量迭代时遇到问题。我在 Stackoverflow 上提了问题 (https://stackoverflow.com/questions/61019185/boostrapped-histogram-of-rmse-for-xgboost-regression-h2o-r-how-to-make-it-more)。
是的。
抱歉,我没有能力为您准备定制代码。
Jason 博士,我有一个问题。如果我碰巧使用随机森林回归器,例如,它已经将自助法作为默认参数,那么是不是就不需要手动应用自助法采样了,对吗?谢谢!
不,我不这么认为。它们是不同的。
模型使用自助法来集成树。
您可以使用自助法来估算模型性能。
你好!我发现这篇帖子非常有帮助,就像其他很多帖子一样:)我只有一个快速问题。
我想知道在您的管道的哪个阶段执行超参数优化(在训练集上使用 10 折交叉验证)。
在您的示例中,您在每次自助法迭代中都在整个训练数据上拟合一个简单的决策树分类器(假设使用默认超参数)。
但如果我想报告最佳优化模型的性能(例如 SVM)以及置信区间,就像您在此处使用此自助法程序所描述的那样,该怎么办?
我是否需要重复超参数调优以在每次自助法迭代中找到训练集上的最佳 C 和 gamma 参数(使用 10 折交叉验证)?
或者,我是否只将其作为自助法重采样之前的最佳模型搜索的初步步骤进行一次?然后使用找到的最佳超参数,在所有迭代的自助法中迭代地拟合我的模型?
谢谢!
不客气。
在重采样过程内部,例如所谓的嵌套交叉验证或嵌套自助法。
或者先选择模型+配置,然后对最终模型使用自助法来估算性能。
只是为了确认,如果您先选择模型+配置,您不能将其选择为初步交叉验证的结果,对吗?如果您先对整个数据集执行交叉验证以选择模型+配置,然后执行自助法来估算性能,那么就会有测试数据泄露。
另外,如果您在重采样过程中进行超参数调优,您实际上会报告哪个模型?相反,每个拟合的模型可能都不会有相同的选定超参数,所以我想您只能说“分类器 X 表现良好”,但不能评论其超参数?
你好 Natalia… 以下资源可能对您感兴趣
https://machinelearning.org.cn/training-validation-test-split-and-cross-validation-done-right/
嗨,Jason,
感谢您的帖子……它非常有帮助和说明性。在尝试执行代码时,我遇到了以下错误。您能否指导我如何解决这个问题?
AttributeError: ‘DataFrame’ object has no attribute ‘tolist’
不客气。
很抱歉听到这个消息,也许这会有帮助
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
另外,pandas 版本是 0.25.1。无需升级。tolist() 的替代方法是什么?
升级到 pandas 1.0.3 或更高版本。
嗨,Jason,
很棒!🙂
我有一个关于这种带放回的自助法方法的测试集大小的疑问。该方法几乎意味着每次迭代的训练集大小相同,但测试集大小不同。例如,我发现我的情况是,测试集大小在 444 到 486 之间变化。
比较/使用由不同测试集大小得出的准确率分数(或其他指标)在一般情况下是可以接受的吗?
还是只能在带放回的自助法方法中接受这种情况,因为没有更好的选择?
谢谢
通常,自助法样本大小配置为与原始数据集大小相同。
你好 Jason,我有一个问题
当我的指标分布不是高斯分布时,我需要改变什么?例如,我为每个自助法创建的指标列表,假设有 3000 个指标,但该列表不遵循高斯分布( Shapiro 测试失败),我该如何创建置信区间?
来自巴西的诚挚问候,
您可以使用自助法直接进行,它不假设分布。
谢谢 Jason,但我不明白为什么不需要假设正态分布,您能解释一下或提供一些链接让我阅读更多内容吗?我一直在阅读关于非参数 CI 的内容,它们具有稳健的数学背景,关于分布,为什么在这种特定情况下不是必需的。
是的,使用自助法的整个想法是因为它是一种非参数方法,不假设分布。
如果您需要更多信息,请参阅“进一步阅读”部分。
Jason,最后一个问题:我可以在测试集上评估 BCI(对该集合进行重采样)来为我的预测创建 95% CI 吗?
我之所以问这个问题,是因为我在 BCI 之前开发了 HP 优化。
它是在一个数据集上计算的,每次运行都有输入和输出样本。严格来说没有训练集和测试集。
这就是我的问题,Jason。我将简要说明我的管道
– 划分训练/测试集
– 在训练集上进行超参数优化 CV 5 折
– 基于我对测试集的预测生成 BCI 区间。也就是说,我从测试集中生成 N 个自助法数据集,计算一个指标,然后在计算 BCI。
我阅读了更多内容,这可能是一个预测区间问题,但我仍然不知道一个好的方法来获得它。我读了您其他的帖子
https://machinelearning.org.cn/report-classifier-performance-confidence-intervals/
我不知道它是否适合我的问题。我不想重新训练我所有的模型……所以某种程度上是否有可能基于测试集预测生成 CI?
感谢分享。
如果对您有用,那太好了,这并非我所说的“方法”。
你好,
在多分类问题中,我很有兴趣知道我的模型的性能(微 F1 分数)是否在基线之上具有统计学意义。因此,我正在寻找 F1 分数的置信区间。
我想使用自助法,但由于我的模型足够大,我无法负担每次都重新训练并计算 F1 分数。
我有一个预测文件,其中包含我的模型对每个测试样本的所有预测。
直接通过对这些预测进行抽样并计算 F1 分数来应用自助法有意义吗?基本上,我会遗漏一些测试样本,在子集上计算 F1 分数并重复,直到我有足够的统计数据来计算置信区间。
如果不行,您有什么建议可以帮助我处理这项任务吗?
提前感谢您!
仓促之间,不行。您将对预测进行抽样,而不是对模型的容量进行抽样。
省略置信区间,使用不同的统计检验,例如
https://machinelearning.org.cn/mcnemars-test-for-machine-learning/
感谢您的快速回复!
我尝试了 McNemar 检验,虽然我仍然有点困惑。此检验是否仅适用于二元分类场景?根据我的理解,2x2 列联表是使用两个模型的预测(无论有多少类别)和基本事实来构建的。
我在互联网上发现 Stuart-Maxwell(或广义 McNemar)检验可用于多分类设置,尽管我在任何 Python 库中都没有找到它的实现(因此我担心其有效性)。
现在,我知道模型 A 的 f1 分数高于模型 B,并且 McNemar 检验得出的 p 值小于临界值,例如 p < 0.05。
我能否得出结论,两个模型性能之间的差异具有统计学意义,即模型 A 优于模型 B?
是的,如果结果更好且有统计学意义,您就可以开始发表声明了。
您可能还想看看 2x5 cv
https://machinelearning.org.cn/hypothesis-test-for-comparing-machine-learning-algorithms/
你好 Jason 和 gonconist,
感谢 Jason 撰写这篇文章。阅读后,我查阅了其他文献,发现“自助法”有两种描述方式
1. 正如您在本文中所解释的,执行重采样并每次训练模型。(“应用预测建模”一书和 Reich, Y. 的论文“评估工程问题的机器学习模型”)
2. 可以将自助法应用于统计估计量以估算其均值和方差。支持此观点的文献
– 书:R 中的统计学习入门(第 5.3.4 节)
– 论文:使用自助法估算神经网络性能:教程(Michelucci, U.)(第 4 节)
因此,为了回答 gonconist 的问题,您建议的方法可以使用。
感谢 balvisio 提供的出色反馈和建议!我们非常感谢!
嗨,Jason!
感谢这篇优秀的帖子。我们正在尝试为 AUC 创建置信区间。我们有一个包含 120k 多条观测值的数据集。我们可以只用 80% 的数据进行重采样并进行训练/测试拆分,而不是进行带放回的自助法吗?或者我们可以多次(数千次)对所有数据进行训练/测试拆分吗?我不太清楚从统计理论的角度来看,为什么要对训练集进行带放回的自助法。毕竟,这会导致训练集出现重复项,而下面的方法则不会。
auc_list = list()
# 开始自助法采样
for i in range(num_iter)
df_resampled = df.sample(frac=0.8, replace=False)
y, X = df_resampled.pop(‘DEATH_90’), df_resampled
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
clf.fit(X_train, y_train)
y_prob = clf.predict_proba(X_test)[:,1]
auc_score = roc_auc_score(y_test, y_prob)
auc_list.append(auc_score)
# 计算下限和上限置信区间
lower_ci = np.percentile(auc_list, ((1.0-alpha)/2.0) * 100)
upper_ci = np.percentile(auc_list, (alpha+((1.0-alpha)/2.0)) * 100)
谢谢你的帮助!
是的,也许可以尝试自助法作为第一步。
抱歉,我没有能力调试您的代码,这些提示可能会有帮助
https://machinelearning.org.cn/faq/single-faq/can-you-read-review-or-debug-my-code
谢谢 Jason。也许我可以不使用任何代码来重述问题。我有一个包含 120k 行的数据集。我可以不使用随机种子并进行数据洗牌来执行 10,000 次训练/测试拆分,这样每次拆分都不同,而不是使用带放回的自助法采样方法?使用我的方法,训练集中不会有重复项,并且训练集和测试集的大小相同。
Nadaa
当然可以。
自助法是在数据量不足时模拟多个样本。
为什么在计算边界时使用最小值和最大值?
最小值和最大值是“边界”的定义。
你好。感谢好帖子。
我有一个问题。
我如何在 keras 的深度学习二元分类中应用此方法?
请帮帮我。
谢谢你
是的,当然。
嗨,Jason,
这篇文章一如既往地对我很有帮助。我有一个问题。当我使用 resample 方法时,它会产生一些 NaN。如何处理这个问题?我的数据集中没有 NaN。
谢谢。
抱歉,我不知道为什么您会得到 NaN。
也许尝试将您的代码和错误发布到 stackoverflow.com
嗨,Jason,
非常好的解释。我想知道如何为多变量非线性模型找到预测区间。我想展示一个预测数据图及其相应的预测区间带。我应该为每个 X 使用预测数据中的百分位数函数吗?
谢谢。
这可能是一个不错的起点
https://machinelearning.org.cn/prediction-intervals-for-machine-learning/
还有这个。
https://machinelearning.org.cn/prediction-intervals-for-deep-learning-neural-networks/
你好,感谢这篇文章。我是一个绝对的初学者,有几个问题。如果能得到您的建议和想法,将非常有帮助。
1.您提到了“95.0 置信区间 64.4% 和 73.0%”——这与说 95% CI [64.4, 73.0] 相同吗?
2. “自助法 Python 库”(https://pypi.ac.cn/project/bootstrapped/)允许您从数据构建置信区间。它不考虑或要求包含 ML 模型。但在您的方法中,您包含了 DecisionTreeClassifier。我想知道这两种计算 CI 的方法的区别是什么?您的方法是否在计算不同的东西?
3. 似乎您正在选择百分位数作为置信区间。但是自助法 Python 库的作者使用的是均值或标准差作为置信区间。这些是可用的不同选项吗?[老实说,我才刚刚开始学习 CI]
4. 您说“使用 95% 置信区间,所以选择 2.5 和 97.5 百分位的值。”——您能解释一下这具体意味着什么吗?您从哪里得到 2.5 和 97.5 这些值?更重要的是,我在您的代码中找不到这些值。那么这些值是如何或在哪里使用的?
1. 是的,我想是的。
2. 我没见过那个库。在这里我们是为模型确定 CI,所以模型包含在代码中。
3. 是的。选择您需要的表示。
4. 是的,请参阅“进一步阅读”部分。
以下是错误的,对吗?
“模型 ROC 曲线下面积性能为 0.59,使用自助法重采样计算的 95% 置信区间为 [0.92-0.96]。”
我使用了您的代码处理我的数据,这是我得到的结果。我可能做错了什么?
也许这会有帮助。
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
或者这个
https://machinelearning.org.cn/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
不确定这是否之前被提及过,但一个更干净、更快的做法是使用 sklearn 的 bagging regressor。它可以比带 for 循环更优化地在内部进行重采样。
https://scikit-learn.cn/stable/modules/generated/sklearn.ensemble.BaggingRegressor.html
感谢分享。
你好,很棒的教程!
我注意到您在这里使用百分位法来计算置信区间,而不是(例如)假设分数遵循正态分布并从中计算 CI。
您是否使用此方法而不是其他方法的原因?此外,是否允许直接从使用百分位法确定的 CI 计算标准误差?
你好 Natalia… 以下资源可能有助于阐明如何以及何时使用百分位。
https://www.uvm.edu/~statdhtx/StatPages/Randomization%20Tests/ResamplingWithR/BootstMeans/bootstrapping_means.html
你好,一如既往的精彩文章。
我实验性地发现 n_size 对置信区间有很大影响。您将其设置为行数的一半,有什么特别的原因吗?我想了解 n_size 的最佳值。
你好 Paul… 以下资源对您在理解和应用优化方面非常有帮助
https://machinelearning.org.cn/optimization-for-machine-learning-crash-course/
你好,非常好的文章!您能否举一个时间序列数据的例子?我的意思是我们如何将自助法应用于时间序列数据
你好 Atish… 以下资源可能有趣
https://stats.stackexchange.com/questions/25706/how-do-you-do-bootstrapping-with-time-series-data
Jason 先生您好
再次感谢这篇好文章。
我有一个问题。这种方法,自助法,与仅使用 CV,如 5 折或 10 折,并获得一些 acc 值有什么区别?
你好… 非常欢迎!以下资源可能有趣
https://machinelearning.org.cn/a-gentle-introduction-to-the-bootstrap-method/
https://machinelearning.org.cn/k-fold-cross-validation/
您好。当我们使用自助法(bootstrapping)来计算样本统计量(例如均值)时,我们不会使用袋外样本(out-of-bag samples)。是否有文献表明我们应该使用OOB来计算模型指标,而不是例如从一个独立的x_train数据集中进行自助采样,并对所有自助样本在同一个x_test上进行预测?