导数是微积分中最基本概念之一。它们描述了变量输入的变化如何影响函数输出。本文的目的是为 PyTorch 新手提供 PyTorch 中导数计算的高级介绍。PyTorch 提供了一种方便的方式来计算用户定义函数的导数。
虽然在神经网络中我们总是需要处理反向传播（一种被称为神经网络骨干的算法），它优化参数以最小化误差，从而实现更高的分类精度；本文中学到的概念将用于后续关于图像处理和其他计算机视觉问题的深度学习文章中。
阅读本教程后，您将学习：
- 如何在 PyTorch 中计算导数。
- 如何在 PyTorch 中使用 autograd 对张量执行自动微分。
- 关于涉及不同节点和叶子的计算图，允许您以尽可能简单的方式（使用链式法则）计算梯度。
- 如何在 PyTorch 中计算偏导数。
- 如何实现函数对多个值的导数。
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧。
在 PyTorch 中计算导数
图片由 Jossuha Théophile 提供。保留部分权利。
Autograd 中的微分
autograd——PyTorch 中的自动微分模块——用于计算导数并优化神经网络中的参数。它主要用于梯度计算。
在开始之前，让我们加载本教程中将用到的一些必要库。
|
1 2 |
import matplotlib.pyplot as plt import torch |
现在，让我们使用一个简单的张量并将 requires_grad 参数设置为 true。这允许我们执行自动微分，并让 PyTorch 使用给定值（在本例中为 3.0）评估导数。
|
1 2 |
x = torch.tensor(3.0, requires_grad = True) print("创建张量 x：", x) |
|
1 |
创建张量 x: tensor(3., requires_grad=True) |
我们将使用一个简单的方程 $y=3x^2$ 作为示例，并对变量 x 求导。因此，让我们根据给定方程创建另一个张量。此外，我们将在变量 y 上应用一个巧妙的方法 .backward，它形成一个存储计算历史的非循环图，并使用 .grad 对给定值评估结果。
|
1 2 3 4 |
y = 3 * x ** 2 print("方程的结果是：", y) y.backward() print("方程在 x = 3 处的导数是：", x.grad) |
|
1 2 |
方程的结果是: tensor(27., grad_fn=<MulBackward0>) 方程在 x = 3 处的导数是: tensor(18.) |
如您所见，我们得到了 18，这是正确的。
计算图
PyTorch 在幕后通过构建一个反向图来生成导数，而张量和反向函数是图的节点。在图中，PyTorch 根据张量是否是叶子来计算其导数。
如果张量的叶子属性设置为 True，PyTorch 将不会评估它的导数。我们不会深入探讨反向图是如何创建和使用的，因为这里的目标是让您对 PyTorch 如何利用图来计算导数有一个高层次的了解。
因此，让我们检查张量 x 和 y 创建后内部的样子。对于 x
|
1 2 3 4 5 |
print('张量的数据属性：',x.data) print('张量的梯度属性：',x.grad) print('张量的 grad_fn 属性：',x.grad_fn) print("张量的 is_leaf 属性：",x.is_leaf) print("张量的 requires_grad 属性：",x.requires_grad) |
|
1 2 3 4 5 |
张量的数据属性： tensor(3.) 张量的梯度属性： tensor(18.) 张量的 grad_fn 属性： None 张量的 is_leaf 属性： True 张量的 requires_grad 属性： True |
对于 y
|
1 2 3 4 5 |
print('张量的数据属性：',y.data) print('张量的梯度属性：',y.grad) print('张量的 grad_fn 属性：',y.grad_fn) print("张量的 is_leaf 属性：",y.is_leaf) print("张量的 requires_grad 属性：",y.requires_grad) |
|
1 2 3 4 5 |
print('张量的数据属性：',y.data) print('张量的梯度属性：',y.grad) print('张量的 grad_fn 属性：',y.grad_fn) print("张量的 is_leaf 属性：",y.is_leaf) print("张量的 requires_grad 属性：",y.requires_grad) |
如您所见，每个张量都分配了一组特定的属性。
data 属性存储张量的数据，而 grad_fn 属性表示图中的节点。同样，.grad 属性保存导数的结果。既然您已经了解了 PyTorch 中 autograd 和计算图的一些基础知识，那么让我们再取一个稍微复杂一点的方程 $y=6x^2+2x+4$ 并计算其导数。该方程的导数由下式给出
$$\frac{dy}{dx} = 12x+2$$
在 $x = 3$ 处评估导数，
$$\left.\frac{dy}{dx}\right\vert_{x=3} = 12\times 3+2 = 38$$
现在，让我们看看 PyTorch 如何做到这一点，
|
1 2 3 4 5 |
x = torch.tensor(3.0, requires_grad = True) y = 6 * x ** 2 + 2 * x + 4 print("方程的结果是：", y) y.backward() print("方程在 x = 3 处的导数是：", x.grad) |
|
1 2 |
方程的结果是: tensor(64., grad_fn=<AddBackward0>) 方程在 x = 3 处的导数是: tensor(38.) |
方程的导数是 38，这是正确的。
想开始使用PyTorch进行深度学习吗？
立即参加我的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
实现函数的偏导数
PyTorch 还允许我们计算函数的偏导数。例如，如果我们要对以下函数应用偏导数，
$$f(u,v) = u^3+v^2+4uv$$
它对 $u$ 的导数是，
$$\frac{\partial f}{\partial u} = 3u^2 + 4v$$
同样，它对 $v$ 的导数将是，
$$\frac{\partial f}{\partial v} = 2v + 4u$$
现在，让我们用 PyTorch 的方式来做，其中 $u = 3$ 和 $v = 4$。
我们将创建 u、v 和 f 张量，并在 f 上应用 .backward 属性以计算导数。最后，我们将使用 .grad 对 u 和 v 的值评估导数。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
u = torch.tensor(3., requires_grad=True) v = torch.tensor(4., requires_grad=True) f = u**3 + v**2 + 4*u*v print(u) print(v) print(f) f.backward() print("对 u 的偏导数：", u.grad) print("对 v 的偏导数：", v.grad) |
|
1 2 3 4 5 |
tensor(3., requires_grad=True) tensor(4., requires_grad=True) tensor(91., grad_fn=<AddBackward0>) 对 u 的偏导数： tensor(43.) 对 v 的偏导数： tensor(20.) |
多值函数的导数
如果我们有一个具有多个值的函数，并且需要计算其对多个值的导数怎么办？为此，我们将使用 sum 属性来 (1) 生成一个标量值函数，然后 (2) 求导。这就是我们如何看待“函数与导数”图：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 计算多值函数的导数 x = torch.linspace(-20, 20, 20, requires_grad = True) Y = x ** 2 y = torch.sum(Y) y.backward() # 绘制函数和导数 function_line, = plt.plot(x.detach().numpy(), Y.detach().numpy(), label = '函数') function_line.set_color("red") derivative_line, = plt.plot(x.detach().numpy(), x.grad.detach().numpy(), label = '导数') derivative_line.set_color("green") plt.xlabel('x') plt.legend() plt.show() |
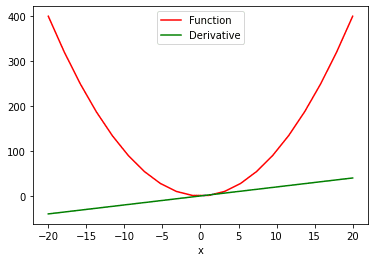
在上面的两个 plot() 函数中，我们从 PyTorch 张量中提取值以便可视化。.detach 方法不允许图进一步跟踪操作。这使我们能够轻松地将张量转换为 numpy 数组。
总结
在本教程中，您学习了如何在 PyTorch 中实现各种函数的导数。
特别是，您学习了
- 如何在 PyTorch 中计算导数。
- 如何在 PyTorch 中使用 autograd 对张量执行自动微分。
- 关于涉及不同节点和叶子的计算图，允许您以尽可能简单的方式（使用链式法则）计算梯度。
- 如何在 PyTorch 中计算偏导数。
- 如何实现函数对多个值的导数。
开始使用PyTorch进行深度学习！
学习如何构建深度学习模型
...使用新发布的PyTorch 2.0库
在我的新电子书中探索如何实现
使用 PyTorch进行深度学习
它提供了包含数百个可用代码的自学教程，让你从新手变成专家。它将使你掌握：
张量操作、训练、评估、超参数优化等等...
哇！这确实太棒了。非常感谢
不客气！
在 Autograd 中的微分部分，你总结道：“方程的导数是 38，这是正确的。”请解释一下
抱歉，是 36 不是 38！
在 Autograd 中的微分部分，您总结道：“如您所见，我们得到了 36，这是正确的。”请解释一下，因为我的结果是 18。
你好 Aliyu……你是怎么得出 18 的？
我是新手，你能解释一下为什么你的最终代码的第 8 行和第 10 行中的逗号是必需的吗？意思是“function_line”和“derivative_line”之后。我发现问题在于，如果没有逗号，“function_line”的类型是“list”，而有逗号时它的类型是“matplotlib.lines.Line2D”。但我找不到为什么会这样的解释。
如果你能解释一下，我将不胜感激。
算了，我已经弄明白了。是为了把它变成一个元组。
我想报告一个错误。在
计算图部分，张量y的属性集没有打印出来。感谢您的反馈，A！
错误百出
## 对于 y：你的代码
print('张量的数据属性：',y.data)
print('张量的梯度属性：',y.grad)
print('张量的 grad_fn 属性：',y.grad_fn)
print("张量的 is_leaf 属性：",y.is_leaf)
print("张量的 requires_grad 属性：",y.requires_grad)
print('张量的数据属性：',y.data)
print('张量的梯度属性：',y.grad)
print('张量的 grad_fn 属性：',y.grad_fn)
print("张量的 is_leaf 属性：",y.is_leaf)
print("张量的 requires_grad 属性：",y.requires_grad)
错误
C:\Users\test\AppData\Local\Temp\ipykernel_17464\1263906903.py:4: UserWarning: 正在访问非叶子张量的 .grad 属性。它的 .grad 属性在 autograd.backward() 期间将不会被填充。如果您确实希望为非叶子张量填充 .grad 字段，请对非叶子张量使用 .retain_grad()。如果您不小心访问了非叶子张量，请确保您访问的是叶子张量。有关更多信息，请参阅 github.com/pytorch/pytorch/pull/30531。（内部触发于 C:\cb\pytorch_1000000000000\work\build\aten\src\ATen/core/TensorBody.h:485。）
print('张量的梯度属性：',y.grad)
C:\Users\test\AppData\Local\Temp\ipykernel_17464\1263906903.py:9: UserWarning: 正在访问非叶子张量的 .grad 属性。它的 .grad 属性在 autograd.backward() 期间将不会被填充。如果您确实希望为非叶子张量填充 .grad 字段，请对非叶子张量使用 .retain_grad()。如果您不小心访问了非叶子张量，请确保您访问的是叶子张量。有关更多信息，请参阅 github.com/pytorch/pytorch/pull/30531。（内部触发于 C:\cb\pytorch_1000000000000\work\build\aten\src\ATen/core/TensorBody.h:485。）
print('张量的梯度属性：',y.grad)
感谢您的反馈！我们非常感谢！
你好，当我们在 pytorch 中计算 MLP 模型输出相对于输入值的导数时，得到的导数是 x*(dy/dx) 还是仅仅是 dy/dx？我想知道我们是否可以使用得到的导数值作为输入的敏感度分数 >
你好 Josh……我们不太明白你的问题。也许你是在问微积分中的链式法则。
尊敬的 Khan 先生，
感谢您的本教程。
PyTorch 版本的微积分与 sympy 包相比如何。
谢谢你
Anthony，悉尼
您好，感谢这篇精彩的教程。PyTorch 可以用来计算函数的高阶导数吗？
你好 Lancelot……应该没有问题。请提供您需要帮助的计算细节，以便我们更好地协助您。