机器学习微积分（7天迷你课程）

作者 Adrian Tam 于 2022年3月16日发布在微积分 28

机器学习速成课程。
在7天内熟悉机器学习中的微积分技术。

微积分是许多机器学习算法背后重要的数学技术。虽然您不一定需要了解它就能使用这些算法，但当您深入研究时，会发现它在关于机器学习模型理论的讨论中无处不在。

作为实践者，我们不太可能遇到非常难的微积分问题。如果我们确实需要解决一个，可以使用计算机代数系统等工具来帮助，或者至少验证我们的解决方案。然而，更重要的是理解微积分背后的思想，并将微积分术语与其在机器学习算法中的应用联系起来。

在本速成课程中，您将探索机器学习中使用的一些常见微积分概念。您将在七天内通过 Python 练习来学习。

这是一篇内容丰富且重要的文章。您可能想把它加入书签。

让我们开始吧。

Calculus for Machine Learning (7-Day Mini-Course)

机器学习的微积分（7天迷你课程）
图片来自 ArnoldReinhold，保留部分权利。

本速成课程适合谁？

在开始之前，让我们确保您来对了地方。

本课程面向可能了解一些应用机器学习的开发人员。也许你知道如何使用流行的工具从头到尾解决预测建模问题，或者至少是大多数主要步骤。

本课程的课程假设您具备以下几点：

您熟悉基本的Python编程。
您可能了解一些基本的线性代数。
您可能了解一些基本的机器学习模型。

您不需要是

成为数学高手！
成为机器学习专家！

本速成课程将带您从一位了解一点机器学习的开发者，成长为一位能够有效地讨论机器学习算法中微积分概念的开发者。

注意：本速成课程假定您有一个可用的 Python 3.7 环境，并安装了一些库，如 SciPy 和 SymPy。如果您在环境设置方面需要帮助，可以遵循此处的循序渐进教程。

如何使用 Anaconda 为机器学习设置你的 Python 环境

速成课程概览

本速成课程分为七节课。

您可以每天完成一节课（推荐），或者在一天内完成所有课程（硬核）。这真的取决于您的可用时间和热情程度。

下面列出了七节课，它们将帮助你开始并高效地使用 Python 进行数据准备

第 01 课：微分
第 02 课：积分
第 03 课：向量函数的梯度
第 04 课：雅可比矩阵
第 05 课：反向传播
第 06 课：优化
第 07 课：支持向量机

每节课可能需要您 5 分钟到 1 小时不等。请按照自己的节奏学习。提问，甚至在下面的评论中发布您的成果。

课程可能需要您自行查找如何操作。我会给您提示，但每节课的一部分意义在于迫使您学习去哪里查找与算法和 Python 中最佳工具相关的信息。（提示：所有答案都在这个博客上；请使用搜索框。）

在评论中发布您的结果；我会为您加油！

坚持下去；不要放弃。

第 01 课：微分

在本课中，您将了解什么是微分或求导。

微分是将一个数学函数转换为另一个称为导数的函数的操作。导数表示原函数的斜率或变化率。

例如，如果我们有一个函数 $f(x)=x^2$，它的导数是一个函数，告诉我们该函数在 $x$ 点的变化率。变化率定义为：$$f'(x) = \frac{f(x+\delta x)-f(x)}{\delta x}$$ 其中 $\delta x$ 是一个很小的量。

通常，我们会将上述定义为极限的形式，即，

$$f'(x) = \lim_{\delta x\to 0} \frac{f(x+\delta x)-f(x)}{\delta x}$$

表示 $\delta x$ 应该尽可能接近零。

有几种求导法则可以帮助我们更容易地找到导数。适合上述例子的一个法则是 $\frac{d}{dx} x^n = nx^{n-1}$。因此，对于 $f(x)=x^2$，我们得到导数 $f'(x)=2x$。

我们可以通过绘制根据变化率计算的函数 $f'(x)$ 与根据求导法则计算的函数进行比较来证实这一点。以下是在 Python 中使用 NumPy 和 matplotlib：

import numpy as np

import matplotlib.pyplot as plt

# 定义函数 f(x)

def f(x):

return x**2

# 计算 f(x) = x^2，x 从 -10 到 10

x = np.linspace(-10,10,500)

y = f(x)

# 在图形的左半部分绘制 f(x)

fig = plt.figure(figsize=(12,5))

ax = fig.add_subplot(121)

ax.plot(x, y)

ax.set_title("y=f(x)")

# 使用变化率计算 f'(x)

delta_x = 0.0001

y1 = (f(x+delta_x) - f(x))/delta_x

# 使用公式计算 f'(x)

y2 = 2 * x

# 在图形的右半部分绘制 f'(x)

ax = fig.add_subplot(122)

ax.plot(x, y1, c="r", alpha=0.5, label="变化率")

ax.plot(x, y2, c="b", alpha=0.5, label="公式")

ax.set_title("y=f'(x)")

ax.legend()

plt.show()

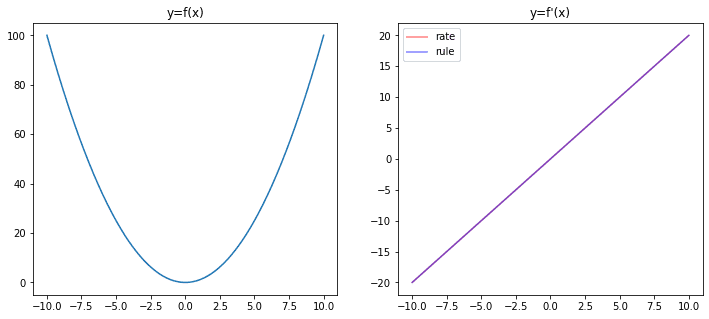
在上图中，我们可以看到通过变化率计算出的导数函数和通过求导法则计算出的导数函数完美地吻合。

您的任务

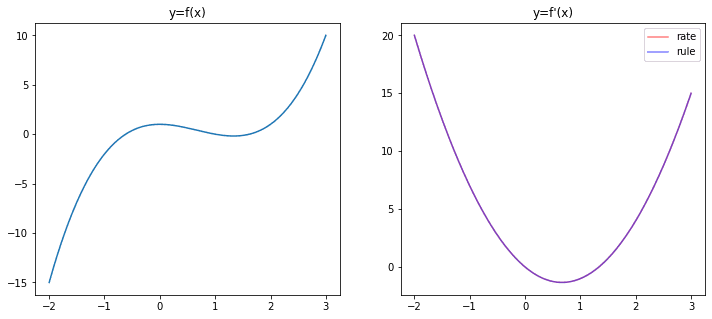
我们可以类似地对其他函数进行微分。例如，$f(x)=x^3 – 2x^2 + 1$。请使用求导法则找到该函数的导数，并将其结果与使用极限变化率得到的结果进行比较。通过上面的图来验证您的结果。如果您操作正确，您应该会看到以下图形。

在下一课中，您将发现积分是微分的逆运算。

第 02 课：积分

在本课中，您将发现积分是微分的逆运算。

如果我们考虑一个函数 $f(x)=2x$，并以 $\delta x$ 的间隔（例如 $\delta x = 0.1$）进行计算，从 $x=-10$ 到 $x=10$ 可以计算为

$$
f(-10), f(-9.9), f(-9.8), \cdots, f(9.8), f(9.9), f(10)
$$

显然，如果 $\delta x$ 越小，上述项就越多。

如果我们把上述每一项乘以步长，然后将它们相加，即：

$$
f(-10)\times 0.1 + f(-9.9)\times 0.1 + \cdots + f(9.8)\times 0.1 + f(9.9)\times 0.1
$$

这个和称为 $f(x)$ 的积分。本质上，这个和是 $f(x)$ 在 $x=-10$ 到 $x=10$ 区间下的**曲线下面积**。微积分中的一个定理表明，如果我们把曲线下面积作为一个函数，它的导数就是 $f(x)$。因此，我们可以将积分视为微分的逆运算。

正如我们在第 01 课中所见，$f(x)=x^2$ 的微分是 $f'(x)=2x$。这意味着对于 $f(x)=2x$，我们可以写成 $\int f(x) dx = x^2$，或者说 $f(x)=x$ 的反导数是 $x^2$。我们可以通过直接计算面积来在 Python 中验证这一点。

import numpy as np

import matplotlib.pyplot as plt

def f(x):

return 2*x

# 设置 x 从 -10 到 10，步长很小

delta_x = 0.1

x = np.arange(-10, 10, delta_x)

# 计算 f(x) * delta_x

fx = f(x) * delta_x

# 计算累加和

y = fx.cumsum()

# 绘制

plt.plot(x, y)

plt.show()

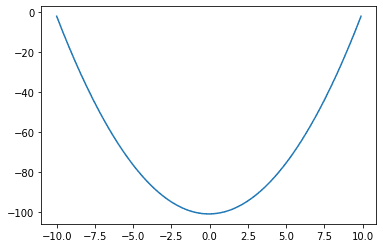
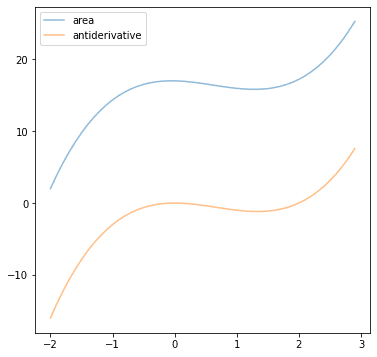
这个图与第 01 课中的 $f(x)$ 形状相同。事实上，所有相差一个常数的函数（例如，$f(x)$ 和 $f(x)+5$）都具有相同的导数。因此，计算出的反导数的图将是原始函数垂直移动后的样子。

您的任务

考虑函数 $f(x)=3x^2-4x$，找到该函数的反导数并绘制它。尝试将上面的 Python 代码替换为这个函数。如果一起绘制两者，您应该看到以下结果。

请在下面的评论中发布您的答案。我很想看看您能想出什么。

第 03 课：向量函数的梯度

在本课中，您将学习多变量函数梯度的概念。

如果我们有一个函数，它不仅有一个变量，而是有两个或更多变量，那么微分自然地扩展为函数对每个变量的微分。例如，如果我们有函数 $f(x,y) = x^2 + y^3$，我们可以写出对每个变量的微分：

$$
\begin{aligned}
\frac{\partial f}{\partial x} &= 2x \\
\frac{\partial f}{\partial y} &= 3y^2
\end{aligned}
$$

这里我们引入了偏导数的符号，意思是当我们计算一个变量的导数时，将其他变量视为常数。因此，在上面，当我们计算 $\frac{\partial f}{\partial x}$ 时，我们忽略了函数 $f(x,y)$ 中的 $y^3$ 部分。

一个有两个变量的函数可以在平面上可视化为一个曲面。上面的函数 $f(x,y)$ 可以使用 matplotlib 进行可视化。

import numpy as np

import matplotlib.pyplot as plt

# 定义 x 和 y 的范围

x = np.linspace(-10,10,1000)

xv, yv = np.meshgrid(x, x, indexing='ij')

# 计算 f(x,y) = x^2 + y^3

zv = xv**2 + yv**3

# 绘制曲面

fig = plt.figure(figsize=(6,6))

ax = fig.add_subplot(projection='3d')

ax.plot_surface(xv, yv, zv, cmap="viridis")

plt.show()

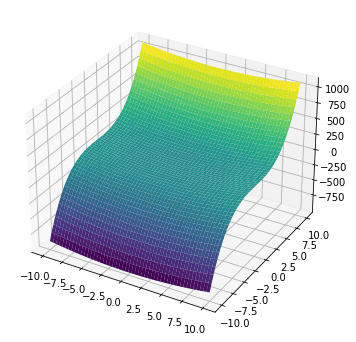
该函数的梯度表示为

$$\nabla f(x,y) = \Big(\frac{\partial f}{\partial x},\; \frac{\partial f}{\partial y}\Big) = (2x,\;3y^2)$$

因此，在每个坐标 $(x,y)$ 处，梯度 $\nabla f(x,y)$ 是一个向量。该向量告诉我们两件事：

向量的方向指向函数 $f(x,y)$ 增长最快的方向。
向量的大小是函数 $f(x,y)$ 在该方向上的变化率。

可视化梯度的一种方法是将其视为一个向量场。

import numpy as np

import matplotlib.pyplot as plt

# 定义 x 和 y 的范围

x = np.linspace(-10,10,20)

xv, yv = np.meshgrid(x, x, indexing='ij')

# 计算 f(x,y) 的梯度

fx = 2*xv

fy = 2*yv

# 将向量 (fx,fy) 转换为大小和方向

size = np.sqrt(fx**2 + fy**2)

dir_x = fx/size

dir_y = fy/size

# 绘制曲面

plt.figure(figsize=(6,6))

plt.quiver(xv, yv, dir_x, dir_y, size, cmap="viridis")

plt.show()

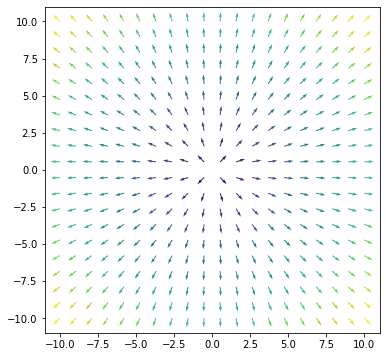
matplotlib 的 viridis 颜色映射将显示较大值（黄色）和较小值（紫色）。因此，我们在上图中看到梯度在边缘比在中心“更陡峭”。

如果我们考虑坐标 (2,3)，我们可以使用以下方法检查 $f(x,y)$ 将沿哪个方向增长最快。

import numpy as np

def f(x, y):

return x**2 + y**3

# 0 到 360 度，步长为 0.1 度

angles = np.arange(0, 360, 0.1)

# 要检查的坐标

x, y = 2, 3

# 微分的步长

step = 0.0001

# 保持最大变化率的大小和方向

maxdf, maxangle = -np.inf, 0

for angle in angles:

# 将角度转换为弧度

rad = angle * np.pi / 180

# 对于固定步长，dx 和 dy

dx, dy = np.sin(rad)*step, np.cos(rad)*step

# 小步长下的变化率

df = (f(x+dx, y+dy) - f(x,y))/step

# 保持最大变化率

if df > maxdf:

maxdf, maxangle = df, angle

# 报告结果

dx, dy = np.sin(maxangle*np.pi/180), np.cos(maxangle*np.pi/180)

gradx, grady = dx*maxdf, dy*maxdf

print(f"在 {maxangle} 度时变化率最大")

print(f"梯度向量在 ({x},{y}) 为 ({dx*maxdf},{dy*maxdf})")

其输出为：

1 2	在 8.4 度时变化率最大梯度向量在 (2,3) 为 (3.987419245872443,27.002750276227097)

根据公式计算出的梯度向量是 (4,27)，上面显示的数值结果非常接近。

您的任务

考虑函数 $f(x,y)=x^2+y^2$，在 (1,1) 处的梯度向量是多少？如果您通过偏微分得到了答案，能否修改上面的 Python 代码，通过检查不同方向上的变化率来验证它？

请在下面的评论中发布您的答案。我很想看看您能想出什么。

在下一课中，您将发现 Jacobian 矩阵在神经网络的反向传播算法中的应用。

第 04 课：雅可比矩阵

在本课中，您将学习雅可比矩阵。

函数 $f(x,y)=(p(x,y), q(x,y))=(2xy, x^2y)$ 是一个具有两个输入和两个输出的函数。有时我们称这种函数为接受向量参数并返回向量值。该函数的微分是一个称为雅可比矩阵的矩阵。上述函数的雅可比矩阵是：

$$
\mathbf{J} =
\begin{bmatrix}
\frac{\partial p}{\partial x} & \frac{\partial p}{\partial y} \\
\frac{\partial q}{\partial x} & \frac{\partial q}{\partial y}
\end{bmatrix}
=
\begin{bmatrix}
2y & 2x \\
2xy & x^2
\end{bmatrix}
$$

在雅可比矩阵中，每一行包含输出向量的每个元素的偏导数，每一列包含相对于输入向量的每个元素的偏导数。

我们稍后会看到雅可比矩阵的用途。由于找到雅可比矩阵涉及大量的偏微分，因此如果能让计算机检查我们的数学计算，那就太好了。在 Python 中，我们可以使用 SymPy 来验证上述结果。

from sympy.abc import x, y

from sympy import Matrix, pprint

f = Matrix([2*x*y, x**2*y])

variables = Matrix([x,y])

pprint(f.jacobian(variables))

其输出为：

⎡ 2⋅y 2⋅x⎤

⎢ ⎥

⎢ 2 ⎥

⎣2⋅x⋅y x ⎦

我们要求 SymPy 定义符号 x 和 y，然后定义向量函数 f。之后，可以通过调用 jacobian() 函数来找到雅可比矩阵。

您的任务

考虑函数
$$
f(x,y) = \begin{bmatrix}
\frac{1}{1+e^{-(px+qy)}} & \frac{1}{1+e^{-(rx+sy)}} & \frac{1}{1+e^{-(tx+uy)}}
\end{bmatrix}
$$

其中 $p,q,r,s,t,u$ 是常数。 $f(x,y)$ 的雅可比矩阵是多少？你能用 SymPy 验证吗？

在下一课中，您将发现 Jacobian 矩阵在神经网络的反向传播算法中的应用。

第 05 课：反向传播

在本课中，您将了解反向传播算法如何使用 Jacobian 矩阵。

如果我们考虑一个只有一个隐藏层的神经网络，我们可以将其表示为一个函数：

$$
y = g\Big(\sum_{k=1}^M u_k f_k\big(\sum_{i=1}^N w_{ik}x_i\big)\Big)
$$

神经网络的输入是一个向量 $\mathbf{x}=(x_1, x_2, \cdots, x_N)$，每个 $x_i$ 将与权重 $w_{ik}$ 相乘后输入到隐藏层。隐藏层中神经元 $k$ 的输出将与权重 $u_k$ 相乘后输入到输出层。隐藏层和输出层的激活函数分别为 $f$ 和 $g$。

如果我们考虑

$$z_k = f_k\big(\sum_{i=1}^N w_{ik}x_i\big)$$

然后

$$
\frac{\partial y}{\partial x_i} = \sum_{k=1}^M \frac{\partial y}{\partial z_k}\frac{\partial z_k}{\partial x_i}
$$

如果我们一次考虑整个层，那么我们有 $\mathbf{z}=(z_1, z_2, \cdots, z_M)$，然后

$$
\frac{\partial y}{\partial \mathbf{x}} = \mathbf{W}^\top\frac{\partial y}{\partial \mathbf{z}}
$$

其中 $\mathbf{W}$ 是 $M\times N$ 的雅可比矩阵，其第 $k$ 行第 $i$ 列的元素是 $\frac{\partial z_k}{\partial x_i}$。

这就是反向传播算法在训练神经网络时的工作方式！对于具有多个隐藏层的网络，我们需要计算每个层的雅可比矩阵。

您的任务

下面的代码实现了一个你可以自己尝试的神经网络模型。它有两个隐藏层和一个用于将二维点分离成两个类的分类网络。尝试查看 `backward()` 函数，并找出雅可比矩阵在哪里。

如果你使用此代码，则 `mlp` 类不应被修改，但你可以更改创建模型时的参数。

from sklearn.datasets import make_circles
from sklearn.metrics import accuracy_score
import numpy as np
np.random.seed(0)

# Find a small float to avoid division by zero
epsilon = np.finfo(float).eps

# Sigmoid function and its differentiation
def sigmoid(z):
    return 1/(1+np.exp(-z.clip(-500, 500)))
def dsigmoid(z):
    s = sigmoid(z)
    return 2 * s * (1-s)

# ReLU function and its differentiation
def relu(z):
    return np.maximum(0, z)
def drelu(z):
    return (z > 0).astype(float)

# Loss function L(y, yhat) and its differentiation
def cross_entropy(y, yhat):
    """Binary cross entropy function
        L = - y log yhat - (1-y) log (1-yhat)

Args:
        y, yhat (np.array): nx1 matrices which n are the number of data instances
    Returns:
        average cross entropy value of shape 1x1, averaging over the n instances
    """
    return ( -(y.T @ np.log(yhat.clip(epsilon)) +
               (1-y.T) @ np.log((1-yhat).clip(epsilon))
              ) / y.shape[1] )

def d_cross_entropy(y, yhat):
    """ dL/dyhat """
    return ( - np.divide(y, yhat.clip(epsilon))
             + np.divide(1-y, (1-yhat).clip(epsilon)) )

class mlp:
    '''Multilayer perceptron using numpy
    '''
    def __init__(self, layersizes, activations, derivatives, lossderiv):
        """remember config, then initialize array to hold NN parameters
        without init"""
        # hold NN config
        self.layersizes = tuple(layersizes)
        self.activations = tuple(activations)
        self.derivatives = tuple(derivatives)
        self.lossderiv = lossderiv
        # parameters, each is a 2D numpy array
        L = len(self.layersizes)
        self.z = [None] * L
        self.W = [None] * L
        self.b = [None] * L
        self.a = [None] * L
        self.dz = [None] * L
        self.dW = [None] * L
        self.db = [None] * L
        self.da = [None] * L

def initialize(self, seed=42):
        """initialize the value of weight matrices and bias vectors with small
        random numbers."""
        np.random.seed(seed)
        sigma = 0.1
        for l, (n_in, n_out) in enumerate(zip(self.layersizes, self.layersizes[1:]), 1):
            self.W[l] = np.random.randn(n_in, n_out) * sigma
            self.b[l] = np.random.randn(1, n_out) * sigma

def forward(self, x):
        """Feed forward using existing `W` and `b`, and overwrite the result
        variables `a` and `z`

Args:
            x (numpy.ndarray): Input data to feed forward
        """
        self.a[0] = x
        for l, func in enumerate(self.activations, 1):
            # z = W a + b, with `a` as output from previous layer
            # `W` is of size rxs and `a` the size sxn with n the number of data
            # instances, `z` the size rxn, `b` is rx1 and broadcast to each
            # column of `z`
            self.z[l] = (self.a[l-1] @ self.W[l]) + self.b[l]
            # a = g(z), with `a` as output of this layer, of size rxn
            self.a[l] = func(self.z[l])
        return self.a[-1]

def backward(self, y, yhat):
        """back propagation using NN output yhat and the reference output y,
        generates dW, dz, db, da
        """
        # first `da`, at the output
        self.da[-1] = self.lossderiv(y, yhat)
        for l, func in reversed(list(enumerate(self.derivatives, 1))):
            # compute the differentials at this layer
            self.dz[l] = self.da[l] * func(self.z[l])
            self.dW[l] = self.a[l-1].T @ self.dz[l]
            self.db[l] = np.mean(self.dz[l], axis=0, keepdims=True)
            self.da[l-1] = self.dz[l] @ self.W[l].T

def update(self, eta):
        """Updates W and b

Args:
            eta (float): Learning rate
        """
        for l in range(1, len(self.W)):
            self.W[l] -= eta * self.dW[l]
            self.b[l] -= eta * self.db[l]

# Make data: Two circles on x-y plane as a classification problem
X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1)
y = y.reshape(-1,1) # our model expects a 2D array of (n_sample, n_dim)

# Build a model
model = mlp(layersizes=[2, 4, 3, 1],
            activations=[relu, relu, sigmoid],
            derivatives=[drelu, drelu, dsigmoid],
            lossderiv=d_cross_entropy)
model.initialize()
yhat = model.forward(X)
loss = cross_entropy(y, yhat)
score = accuracy_score(y, (yhat > 0.5))
print(f"Before training - loss value {loss} accuracy {score}")

# train for each epoch
n_epochs = 150
learning_rate = 0.005
for n in range(n_epochs):
    model.forward(X)
    yhat = model.a[-1]
    model.backward(y, yhat)
    model.update(learning_rate)
    loss = cross_entropy(y, yhat)
    score = accuracy_score(y, (yhat > 0.5))
    print(f"Iteration {n} - loss value {loss} accuracy {score}")

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

from sklearn.datasets import make_circles

from sklearn.metrics import accuracy_score

import numpy as np

np.random.seed(0)

# 查找一个很小的浮点数以避免除以零

epsilon = np.finfo(float).eps

# Sigmoid 函数及其导数

def sigmoid(z):

return 1/(1+np.exp(-z.clip(-500, 500)))

def dsigmoid(z):

s = sigmoid(z)

return 2 * s * (1-s)

# ReLU 函数及其导数

def relu(z):

return np.maximum(0, z)

def drelu(z):

return (z > 0).astype(float)

# 损失函数 L(y, yhat) 及其导数

def cross_entropy(y, yhat):

"""二元交叉熵函数

L = - y log yhat - (1-y) log (1-yhat)

参数

y, yhat (np.array): nx1 矩阵，其中 n 是数据实例的数量

平均交叉熵值，形状为 1x1，对 n 个实例进行平均

"""

return ( -(y.T @ np.log(yhat.clip(epsilon)) +

(1-y.T) @ np.log((1-yhat).clip(epsilon))

) / y.shape[1] )

def d_cross_entropy(y, yhat):

""" dL/dyhat """

return ( - np.divide(y, yhat.clip(epsilon))

+ np.divide(1-y, (1-yhat).clip(epsilon)) )

class mlp:

'''使用numpy实现的多层感知机

'''

def __init__(self, layersizes, activations, derivatives, lossderiv):

"""记住配置，然后初始化用于保存 NN 参数的数组

无初始化"""

# 保存 NN 配置

self.layersizes = tuple(layersizes)

self.activations = tuple(activations)

self.derivatives = tuple(derivatives)

self.lossderiv = lossderiv

# 参数，每个都是一个二维 numpy 数组

L = len(self.layersizes)

self.z = [None] * L

self.W = [None] * L

self.b = [None] * L

self.a = [None] * L

self.dz = [None] * L

self.dW = [None] * L

self.db = [None] * L

self.da = [None] * L

def initialize(self, seed=42):

"""使用小的随机数初始化权重矩阵和偏置向量的值

随机数。"""

np.random.seed(seed)

sigma = 0.1

for l, (n_in, n_out) in enumerate(zip(self.layersizes, self.layersizes[1:]), 1):

self.W[l] = np.random.randn(n_in, n_out) * sigma

self.b[l] = np.random.randn(1, n_out) * sigma

def forward(self, x):

"""使用现有的 `W` 和 `b` 进行前向传播，并覆盖结果

变量 `a` 和 `z`

参数

x (numpy.ndarray): 输入到前向传播的数据

"""

self.a[0] = x

for l, func in enumerate(self.activations, 1):

# z = W a + b，其中 `a` 是前一层的输出

# `W` 的大小为 rxs，`a` 的大小为 sxn，其中 n 是数据数量

# 实例，`z` 的大小为 rxn，`b` 为 rx1 并广播到 `z` 的每个

# 列

self.z[l] = (self.a[l-1] @ self.W[l]) + self.b[l]

# a = g(z)，其中 `a` 是此层的输出，大小为 rxn

self.a[l] = func(self.z[l])

return self.a[-1]

def backward(self, y, yhat):

"""使用 NN 输出 yhat 和参考输出 y 进行反向传播，

生成 dW, dz, db, da

"""

# 首先是 `da`，在输出层

self.da[-1] = self.lossderiv(y, yhat)

for l, func in reversed(list(enumerate(self.derivatives, 1))):

# 计算此层的微分

self.dz[l] = self.da[l] * func(self.z[l])

self.dW[l] = self.a[l-1].T @ self.dz[l]

self.db[l] = np.mean(self.dz[l], axis=0, keepdims=True)

self.da[l-1] = self.dz[l] @ self.W[l].T

def update(self, eta):

"""更新 W 和 b

参数

eta (float): 学习率

"""

for l in range(1, len(self.W)):

self.W[l] -= eta * self.dW[l]

self.b[l] -= eta * self.db[l]

# 制作数据：xy 平面上的两个圆圈作为分类问题

X, y = make_circles(n_samples=1000, factor=0.5, noise=0.1)

y = y.reshape(-1,1) # 我们的模型期望一个 (n_sample, n_dim) 的二维数组

# 构建一个模型

model = mlp(layersizes=[2, 4, 3, 1],

activations=[relu, relu, sigmoid],

derivatives=[drelu, drelu, dsigmoid],

lossderiv=d_cross_entropy)

model.initialize()

yhat = model.forward(X)

loss = cross_entropy(y, yhat)

score = accuracy_score(y, (yhat > 0.5))

print(f"训练前 - loss 值 {loss} 准确率 {score}")

# 训练每个 epoch

n_epochs = 150

learning_rate = 0.005

for n in range(n_epochs):

model.forward(X)

yhat = model.a[\-1]

model.backward(y, yhat)

model.update(learning_rate)

loss = cross_entropy(y, yhat)

score = accuracy_score(y, (yhat > 0.5))

print(f"迭代 {n} - loss 值 {loss} 准确率 {score}")

在下一课中，你将了解如何使用微分来找到函数的最佳值。

第 06 课：优化

在本课中，你将学习微分的一个重要用途。

由于函数的微分是变化率，我们可以利用微分来找到函数的最佳点。

如果一个函数达到了它的最大值，我们预期它会从一个较低的点移动到最大值，如果我们再往前进，它会落到另一个较低的点。因此，在最大值点，函数的改变速率为零。最小值也是如此。

例如，考虑函数 $f(x)=x^3-2x^2+1$。其导数为 $f'(x) = 3x^2-4x$，并且 $f'(x)=0$ 在 $x=0$ 和 $x=4/3$ 处成立。因此，这些 $x$ 的位置是 $f(x)$ 达到最大值或最小值的地方。我们可以通过绘制 $f(x)$ 的图像来直观地证实这一点（参见第 01 课的图）。

你的任务

考虑函数 $f(x)=\log x$ 并找到其导数。当 $f'(x)=0$ 时，$x$ 的值为多少？这对对数函数的最大值或最小值有什么启示？尝试绘制 $\log x$ 的函数图，以直观地确认你的答案。

在下一课中，你将了解此技术在查找支持向量中的应用。

第 07 课：支持向量机

在本课中，你将学习如何将支持向量机转化为一个优化问题。

在二维平面上，任何直线都可以用以下方程表示：

$$ax+by+c=0$$

在 $xy$ 坐标系中。坐标几何学研究的一个结果表明，对于任何点 $(x_0,y_0)$，它到直线 $ax+by+c=0$ 的距离为：

$$
\frac{\vert ax_0+by_0+c \vert}{\sqrt{a^2+b^2}}
$$

考虑 $xy$ 平面上的点 (0,0)、(1,2) 和 (2,1)，其中第一个点和后两个点属于不同的类别。什么直线能够最好地分隔这两个类别？这就是支持向量机分类器的基础。在这个例子中，支持向量是最大间隔的直线。

为了找到这样的直线，我们正在寻找

$$
\begin{aligned}
\text{最小化} && a^2 + b^2 \\
\text{约束条件为} && -1(0a+0b+c) &\ge 1 \\
&& +1(1a+2b+c) &\ge 1 \\
&& +1(2a+1b+c) &\ge 1
\end{aligned}
$$

目标 $a^2+b^2$ 被最小化，以便数据点到直线的距离最大化。条件 $-1(0a+0b+c)\ge 1$ 意味着点 (0,0) 属于类别 $-1$；其他两个点也类似，它们属于类别 $+1$。直线应该将这两个类别放置在平面的不同侧。

这是一个约束优化问题，解决方法是使用拉格朗日乘数法。使用拉格朗日乘数法的第一个步骤是找到以下拉格朗日函数的偏导数：

$$
L = a^2+b^2 + \lambda_1(-c-1) + \lambda_2 (a+2b+c-1) + \lambda_3 (2a+b+c-1)
$$

并将偏导数设为零，然后求解 $a$、$b$ 和 $c$。在这里详细演示会太冗长，但我们可以使用 SciPy 以数值方式找到上述问题的解。

import numpy as np

from scipy.optimize import minimize

def objective(w):

return w[0]**2 + w[1]**2

def constraint1(w):

"点 (0,0) 的不等式"

return -1*w[2] - 1

def constraint2(w):

"点 (1,2) 的不等式"

return w[0] + 2*w[1] + w[2] - 1

def constraint3(w):

"点 (2,1) 的不等式"

return 2*w[0] + w[1] + w[2] - 1

# 初始猜测

w0 = np.array([1, 1, 1])

# 优化

bounds = ((-10,10), (-10,10), (-10,10))

constraints = [

{"type":"ineq", "fun":constraint1},

{"type":"ineq", "fun":constraint2},

{"type":"ineq", "fun":constraint3},

]

solution = minimize(objective, w0, method="SLSQP", bounds=bounds, constraints=constraints)

w = solution.x

print("目标函数值：", objective(w))

print("解：", w)

输出将是：

1 2	目标函数值： 0.8888888888888942 解： [ 0.66666667 0.66666667 -1. ]

以上意味着分隔这三个点的直线是 $0.67x + 0.67y – 1 = 0$。请注意，如果您提供了 $N$ 个数据点，就需要定义 $N$ 个约束条件。

您的任务

考虑点 (-1,-1) 和 (-3,-1) 作为第一类，以及 (0,0) 和点 (3,3) 作为第二类，以及点 (1,2) 和 (2,1)。在这六个点的问题中，你能修改上面的程序来找到分隔这两个类别的直线吗？看到结果与上面相同不要感到惊讶。这其中是有原因的。你能说出来吗？

请在下面的评论中发布您的答案。我很想看看您能想出什么。

这是最后一课。

结束！
(看看您取得了多大的进步)

您做到了。干得好！

花点时间回顾一下您已经走了多远。

您发现了：

什么是微分，它对函数意味着什么
什么是积分
如何将微分扩展到向量自变量的函数
如何对向量值函数进行微分
雅可比矩阵在神经网络反向传播算法中的作用
如何使用微分来查找函数的最佳点
支持向量机是一个约束优化问题，需要微分来解决。

总结

您对这个迷你课程的学习情况如何？
您喜欢这个速成课程吗？

您有任何问题吗？有没有遇到什么难点？
告诉我。在下面留言。

关于此主题的更多信息

探索 Python 生态系统

使用 matplotlib、Seaborn 和 Bokeh 在 Python 中进行数据可视化

对机器学习中的微积分（7 天迷你课程）的 28 条回复

Harlincoln 2022 年 3 月 17 日凌晨 12:43 #

我将获得证书或某种证明我完成了这个“机器学习微积分”课程的东西吗？
如果可以，那我将毫不犹豫地参加这个课程！

回复
- James Carmichael 2022 年 3 月 17 日下午 12:42 #
  
  你好 Harlincoln…没有证书，但是完成课程后，你对微积分的信心会大大增强。
  
  回复
Charlie 2022 年 3 月 17 日凌晨 3:52 #

Jason，

当我输入第一个迷你课程的代码时，我收到了错误消息：

AttributeError: ‘AxesSubplot’ object has no attribute ‘plt’

我在 Stack Overflow 上搜索并谷歌搜索了它……找不到解决方案……我正在使用 Jupyter Notebooks (anaconda) 和 Windows 10 作为操作系统。我的笔记本环境是 py3-TF2.0。

我哪里做错了？

回复
- James Carmichael 2022 年 3 月 17 日下午 12:40 #
  
  你好 Charlie…以下资源可能有所帮助
  
  https://www.statology.org/module-matplotlib-has-no-attribute-plot/
  
  回复
Chinmayee 2022 年 3 月 18 日上午 5:40 #

你好，我很喜欢这个迷你课程。我觉得它非常有信息量和实用。我可以完成所有课程，但对于最后一课，我得到了与上面相同的解决方案，但相同解决方案背后的原因是什么？

对于第 6 课，我发现最大值在 x=infinity 处，对于第 5 课，雅可比矩阵是 dz[ l ] 矩阵。
第 4 课，(1,1) 处的梯度向量是 (2.000070710675876,2.0000707106758764)。我无法在此处共享图。

感谢这门课程。
此致

回复
Srini 2022 年 3 月 18 日下午 4:44 #

你好，
有人能解释一下我如何表示下面的符号，就像数学符号一样吗？用什么数学工具来可视化这个表达式？

$$f'(x) = \lim_{\delta x\to 0} \frac{f(x+\delta x)-f(x)}{\delta x}$$

谢谢
GL

回复
- James Carmichael 2022 年 3 月 20 日上午 7:23 #
  
  你好 Srini…以下工具可能对您有帮助：
  
  https://tutorialspoint.org.cn/latex_equation_editor.htm
  
  回复
Ricardo Montañana 2022 年 3 月 18 日晚上 9:23 #

非常感谢您提供如此好的带有例子的解释！

回复
Jakob 2022 年 3 月 18 日晚上 11:30 #

嗨！

这是我为第 2 课写出的代码：

def f(x)
return (3*x**2) – (4*x)

def ff(x)
return (x**3) – (2*x**2)

delta_x = 0.1
x = np.arange(-10,10,delta_x)
fx = f(x) * delta_x
y = fx.cumsum()

plt.plot(x, y)
plt.plot(x, ff(x))
plt.show

回复
- James Carmichael 2022 年 3 月 20 日上午 7:21 #
  
  感谢 Jakob 的反馈！
  
  回复
Charles 2022 年 3 月 19 日凌晨 2:55 #

当我输入积分时，只得到了上面的曲线；程序没有重现下面的曲线……

回复
- James Carmichael 2022 年 3 月 20 日上午 7:18 #
  
  你好 Charles…你是否复制粘贴了代码还是自己输入的？
  
  回复
Heinz 2022 年 3 月 19 日上午 9:00 #

你好，
我有一个关于第 03 课的问题，第二个代码框，第 10 行：这不应该读作 “fy = 3*yv**2”，因为 $y^3$ 的微分是 $3y^2$ 吗？

回复
- James Carmichael 2022 年 3 月 20 日上午 7:15 #
  
  你好 Heinz…请发布您所指的确切行。
  
  回复
  - Andreas 2023 年 2 月 19 日上午 8:36 #
    
    Heinz 说的就是这些行：
    
    # 计算 f(x,y) 的梯度
    fx = 2*xv
    fy = 2*yv
    
    这实际上应该是：
    # 计算 f(x,y) 的梯度
    fx = 2*xv
    fy = 3*yv**2
    
    这样的话，生成的向量场就对应于上面函数 $f(x,y) = x^2 + y^3$ 的图了。
    
    总之，感谢您的教程，到目前为止它非常有帮助。
    
    回复
    - James Carmichael 2023 年 2 月 19 日上午 9:12 #
      
      谢谢你的反馈！
      
      回复
Stephen Nkonde 2022 年 3 月 20 日上午 5:45 #

结果不会一致，因为函数有一个立方根、一个平方根和一个常数。这是我的想法，Jason 请帮助我。
Jason@machinelearningmastery.com.

回复
- James Carmichael 2022 年 3 月 20 日上午 7:04 #
  
  你好 Stephen…请说明你认为哪个结果有问题，以便我们能更好地帮助你。
  
  回复
Thin Htoo Han 2022 年 3 月 20 日下午 4:49 #

你好，

在第 3 课中，我并不清楚为什么 delta x 是通过将步长乘以角度的正弦而不是余弦来计算的。我认为 x 分量是通过乘以角度的余弦得到的。如果您有时间解释一下，我将不胜感激。谢谢！

回复
- James Carmichael 2022 年 3 月 21 日下午 12:20 #
  
  你好 Thin…正弦的导数是余弦。
  
  回复
Emad A. Ismael 2022 年 3 月 21 日上午 4:16 #

#!/home/emad/anaconda3/bin/python

import numpy as np
import matplotlib.pyplot as plt

def f(x)
return 3 * x**2 – 4 * x

def finteg(x)
return x**3 – 2 * x**2

def compute_area_under_curve()
# 设置 x 从 -10 到 10，步长很小
delta_x = 0.1
x = np.arange(-10, 10, delta_x)
# 计算 f(x) * delta_x
fx = f(x) * delta_x
# 计算累加和
y = fx.cumsum()
return x, y

def compute_antiderivative_points()
delta_x = 0.1
x = np.arange(-10, 10, delta_x)
y = finteg(x)
return x, y

def plot_curve(x, y, x1, y1)
plt.plot(x, y, c=”r”, alpha=0.5, label=”antiderivative”)
plt.plot(x1, y1, c=”b”, alpha=0.5, label=”area”)
plt.legend()
plt.show()

def main()
# 绘制反导数
x1, y1 = compute_antiderivative_points()

# 绘制曲线下面积
x, y = compute_area_under_curve()

plot_curve(x, y, x1, y1)

if __name__ == “__main__”
main()

回复
- James Carmichael 2022 年 3 月 21 日下午 12:15 #
  
  继续努力 Emad！
  
  回复
sahil 2022 年 3 月 31 日凌晨 1:05 #

import numpy as np
def f(x, y)
return x**2+y**2
angles=np.arange(0, 360, 0.1)
x,y=1, 1
step=0.0001
maxdf, maxangle= -np.inf, 0
for angle in angles
rad = angle * np.pi / 180
dx, dy= np.sin(rad)*step, np.cos(rad)*step
df = (f(x+dx, y+dy) – f(x,y))/step
if df > maxdf
maxdf, maxangle= df, angle
dx,dy=np.sin(maxangle*np.pi/180), np.cos(maxangle*np.pi/180)
gradx,grady=dx*maxdf, dy*maxdf
print(f”在 {maxangle} 度时的最大变化率”)
print(f”({x},{y}) 处的梯度向量是 ({dx*maxdf},{dy*maxdf})”)

在 359.90000000000003 度时的最大变化率
在 (1,1) 处的梯度向量是 (-0.0034847336058503437,1.9966032560898956)
我检查了代码，与您的代码没有不正确之处，但仍然得到上述错误的答案，您能告诉我我做错了什么吗？？

回复
- James Carmichael 2022 年 3 月 31 日上午 9:19 #
  
  你好 Sahil…谢谢你的提问。
  
  我很想帮忙，但我实在没有能力为您调试代码。
  
  我很乐意提出一些建议
  
  考虑将代码积极削减到最低要求。这将帮助您隔离问题并专注于它。
  考虑将问题简化为一个或几个简单的例子。
  考虑寻找其他可行的类似代码示例，并慢慢修改它们以满足您的需求。这可能会暴露您的失误。
  考虑在 StackOverflow 上发布您的问题和代码。
  
  回复
Sumit 2022 年 6 月 22 日晚上 9:36 #

你好，

我最近完成了关于导数的章节，并按照课程中的解释实现了微分公式。我的代码给了我很好的输出，并且我能够成功计算所有 T 值的导数。然而，当我尝试指数函数时，我的代码就崩溃了。我检查了 $e^x$ 的值列表，发现列表如预期的指数函数一样迅速增长，值高达 $10^{43}$。

我知道一个称为灾难性抵消的术语，它在数值方法中非常常见，我认为是因为步长太小且输入值非常大，导致分子中的差值爆炸，系统饱和为 0。有什么方法可以验证这是否真的发生？如果确实如此，有什么方法可以解决这个问题？

回复
- James Carmichael 2022 年 6 月 23 日上午 10:58 #
  
  你好 Sumit…请更详细地说明你的代码“崩溃”是什么意思，以便我们能更好地帮助你。
  
  回复
Alradaee 2022 年 12 月 11 日凌晨 2:31 #

非常感谢您提供如此精彩的教程。
如果可能的话，我希望您能帮助我为我的计算机视觉或 NLP 硕士论文找到一个主题。

回复
- James Carmichael 2022 年 12 月 11 日上午 9:33 #
  
  你好 Alradaee…虽然我们无法推荐一个研究课题，但我们建议以下资源作为起点：
  
  https://machinelearning.org.cn/deep-learning-for-nlp/
  
  回复

导航

机器学习微积分（7天迷你课程）

机器学习速成课程。
在7天内熟悉机器学习中的微积分技术。

本速成课程适合谁？

速成课程概览

第 01 课：微分

您的任务

第 02 课：积分

您的任务

第 03 课：向量函数的梯度

您的任务

第 04 课：雅可比矩阵

您的任务

第 05 课：反向传播

您的任务

第 06 课：优化

你的任务

第 07 课：支持向量机

您的任务

结束！
(看看您取得了多大的进步)

总结

掌握机器学习微积分！

通过微积分概念变得更聪明

将恰到好处的微积分知识带到
您的机器学习项目

关于此主题的更多信息

对机器学习中的微积分（7 天迷你课程）的 28 条回复

Leave a Reply Click here to cancel reply.

导航

机器学习速成课程。在7天内熟悉机器学习中的微积分技术。

本速成课程适合谁？

速成课程概览

第 01 课：微分

您的任务

第 02 课：积分

您的任务

第 03 课：向量函数的梯度

您的任务

第 04 课：雅可比矩阵

您的任务

第 05 课：反向传播

您的任务

第 06 课：优化

你的任务

第 07 课：支持向量机

您的任务

结束！(看看您取得了多大的进步)

总结

掌握机器学习微积分！

通过微积分概念变得更聪明

将恰到好处的微积分知识带到您的机器学习项目

关于此主题的更多信息

对 机器学习中的微积分（7 天迷你课程） 的 28 条回复

Leave a Reply Click here to cancel reply.

机器学习速成课程。
在7天内熟悉机器学习中的微积分技术。

结束！
(看看您取得了多大的进步)

将恰到好处的微积分知识带到
您的机器学习项目

对机器学习中的微积分（7 天迷你课程）的 28 条回复