微积分是机器学习中的核心数学概念之一，它使我们能够理解不同机器学习算法的内部工作原理。
微积分在机器学习中的一个重要应用是梯度下降算法，该算法与反向传播相结合，使我们能够训练神经网络模型。
在本教程中，您将了解微积分在机器学习中的重要作用。
完成本教程后，您将了解：
- 微积分在理解机器学习算法（例如用于最小化误差函数的梯度下降算法）的内部工作原理方面起着不可或缺的作用。
- 微积分为我们提供了优化复杂目标函数以及具有多维输入的函数所需的工具，这些函数代表了不同的机器学习应用。
让我们开始吧。
机器学习中的微积分：为何有效
图片来源：Hasmik Ghazaryan Olson，保留部分权利。
教程概述
本教程分为两部分；它们是
- 机器学习中的微积分
- 为什么微积分在机器学习中有效
机器学习中的微积分
神经网络模型，无论是浅层还是深层，都实现了一个将一组输入映射到预期输出的函数。
神经网络实现的函数通过训练过程学习，该过程迭代搜索一组权重，这些权重能够最佳地使神经网络模拟训练数据中的变化。
一种非常简单的函数是将单个输入线性映射到单个输出。
第187页，深度学习，2019。
这种线性函数可以用具有斜率m和y截距c的直线方程表示。
y = mx + c
改变参数m和c中的每一个都会产生不同的线性模型，这些模型定义了不同的输入-输出映射。
通过改变斜率和截距产生的不同线模型的线图
摘自《深度学习》
因此，学习映射函数的过程涉及近似这些模型参数或权重，以使预测输出和目标输出之间的误差最小化。这个误差通过损失函数、成本函数或误差函数（通常可互换使用）计算，最小化损失的过程称为函数优化。
我们可以将微分微积分应用于函数优化过程。
为了更好地理解微分微积分如何应用于函数优化，让我们回到我们线性映射函数的具体示例。
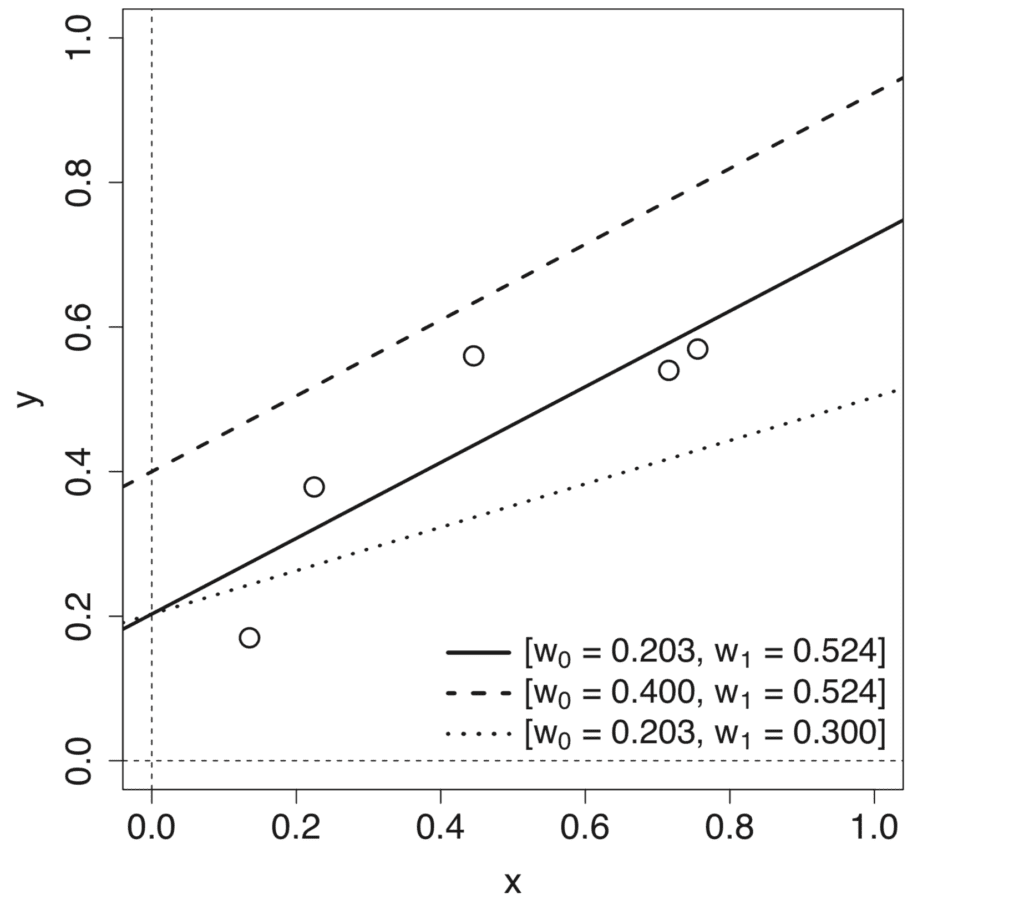
假设我们有一些包含单个输入特征x及其对应目标输出y的数据集。为了测量数据集上的误差，我们将把预测输出和目标输出之间的平方误差和（SSE）作为我们的损失函数。
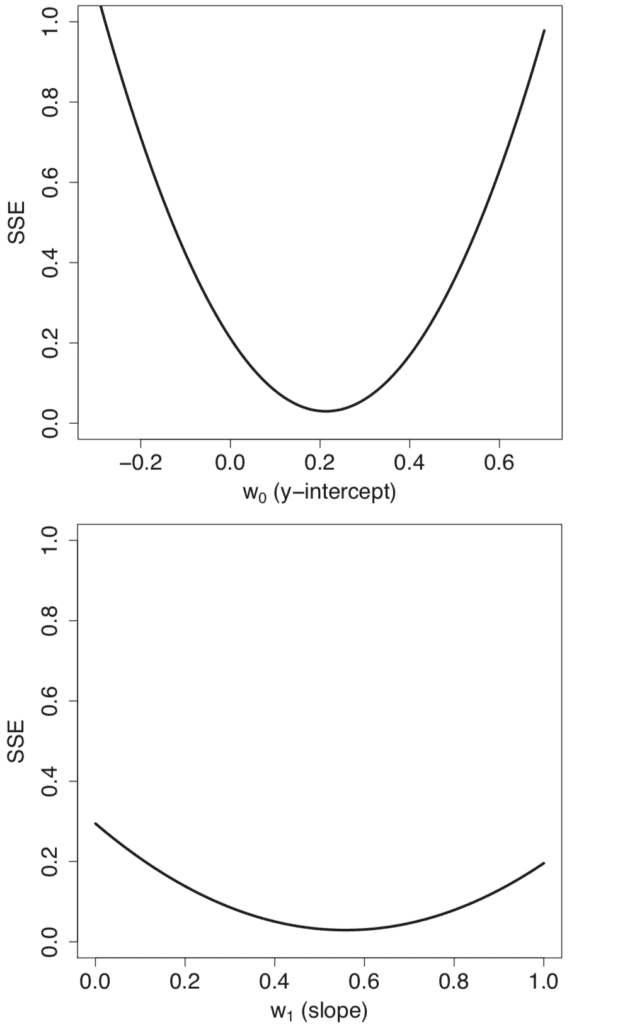
对模型权重w0 = m和w1 = c的不同值进行参数扫描，会生成形状凸起的独立误差曲线。
在斜率和截距的一系列值上进行扫描时生成的误差 (SSE) 曲线的线图
摘自《深度学习》
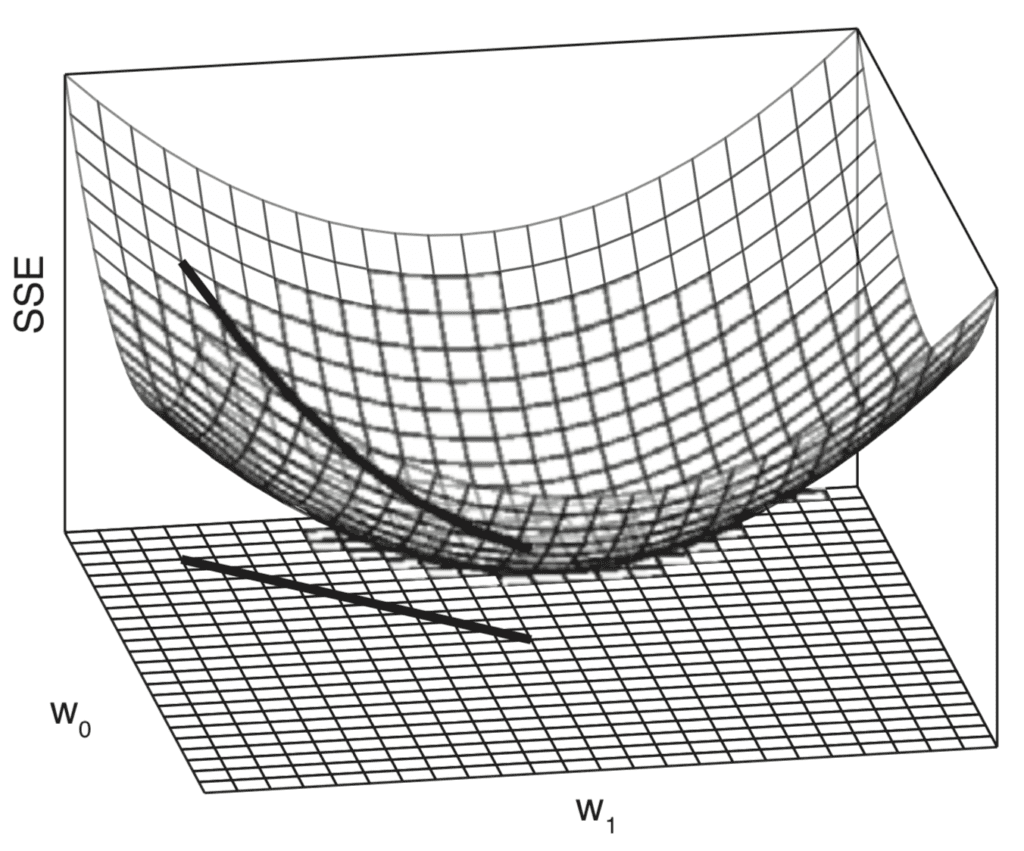
将单个误差剖面结合起来会生成一个三维误差曲面，该曲面也是凸形的。这个误差曲面包含在一个权重空间中，该空间由模型权重w0和w1的扫描值范围定义。
斜率和截距都变化时生成的误差 (SSE) 曲面的三维图
摘自《深度学习》
在这个权重空间中移动等同于在不同的线性模型之间移动。我们的目标是从所有可能的替代方案中识别出最适合数据的模型。最佳模型的特点是数据集上的误差最低，这对应于误差曲面上的最低点。
一个凸形或碗形的误差曲面对于学习线性函数来建模数据集非常有用，因为它意味着学习过程可以被框定为在误差曲面上寻找最低点的过程。用于找到这个最低点的标准算法被称为梯度下降。
第194页，深度学习，2019。
梯度下降算法作为优化算法，将通过沿着误差曲面向下梯度寻找最低点。这种下降是基于对误差曲面梯度或斜率的计算。
这就是微分微积分发挥作用的地方。
微积分，特别是微分，是处理变化率的数学领域。
第198页，深度学习，2019。
更正式地，让我们用以下方式表示我们想要优化的函数：
误差 = f(权重)
通过计算误差相对于权重的变化率或斜率，梯度下降算法可以决定如何改变权重以持续减小误差。
为什么微积分在机器学习中有效
我们考虑优化的误差函数相对简单，因为它是一个凸函数，并且具有一个全局最小值。
然而，在机器学习中，我们通常需要优化更复杂的函数，这使得优化任务变得非常具有挑战性。如果函数的输入也是多维的，优化可能会变得更加困难。
微积分为我们提供了应对这两个挑战所需的工具。
假设我们有一个更通用的函数需要最小化，它接受一个实数输入x，生成一个实数输出y
y = f(x)
计算x不同值的变化率很有用，因为它可以指示我们需要对x应用哪些更改，以便在y中获得相应的更改。
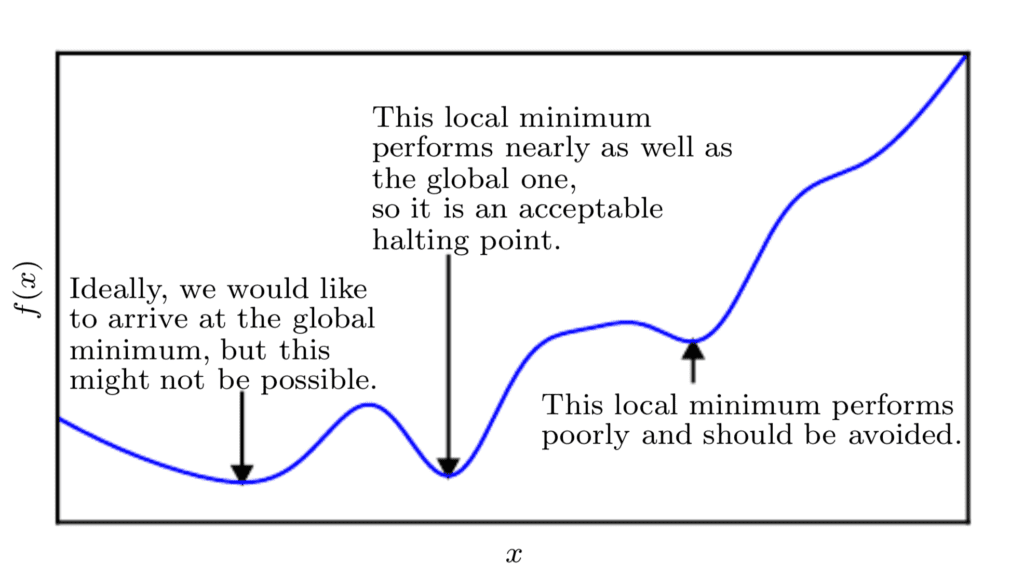
由于我们正在最小化函数，我们的目标是达到一个点，该点获得尽可能低的f(x)值，并且其变化率为零；因此，达到全局最小值。根据函数的复杂性，这可能不一定能够实现，因为可能存在许多局部最小值或鞍点，优化算法可能会陷入其中。
在深度学习的背景下，我们优化的函数可能有很多不是最优的局部最小值，以及许多被非常平坦区域包围的鞍点。
第84页，深度学习，2017。
因此，在深度学习的背景下，我们通常接受一个次优解，该解不一定对应于全局最小值，只要它对应于f(x)的一个非常低的值。
要最小化的成本函数的线图，显示局部最小值和全局最小值
摘自《深度学习》
如果我们处理的函数接受多个输入，微积分也为我们提供了偏导数的概念；或者简单来说，这是一种计算y相对于每个输入xi的变化率的方法，同时保持其余输入不变。
这就是为什么在梯度下降算法中每个权重都是独立更新的：权重更新规则取决于每个权重的 SSE 的偏导数，并且由于每个权重都有不同的偏导数，因此每个权重都有一个单独的权重更新规则。
第200页，深度学习，2019。
因此，如果我们再次考虑误差函数的最小化，计算误差相对于每个特定权重的偏导数，就可以使每个权重独立于其他权重进行更新。
这也意味着梯度下降算法可能不会沿着误差曲面直线下降。相反，每个权重将按误差曲线的局部梯度比例更新。因此，一个权重可能比另一个权重更新的幅度更大，以达到梯度下降算法的函数最小值所需的程度。
进一步阅读
如果您想深入了解，本节提供了更多关于该主题的资源。
书籍
总结
在本教程中，您了解了微积分在机器学习中的重要作用。
具体来说，你学到了：
- 微积分在理解机器学习算法的内部工作原理方面起着不可或缺的作用，例如基于变化率计算来最小化误差函数的梯度下降算法。
- 微积分中变化率的概念也可以用来最小化不一定呈凸形的更复杂的目标函数。
- 偏导数的计算是微积分中另一个重要的概念，它使我们能够处理接受多个输入的函数。
你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。
谢谢您的教程。
在训练具有多个局部最优点的DL/ML模型时，如何保证模型找到的局部最优解是其中最低或最高的？以及如何克服模型停滞在最高的局部最优解的情况？
谢谢/
引用自《模式识别与机器学习》：“对于神经网络的成功应用，不一定需要找到全局最小值（通常也无法得知是否找到了全局最小值），但可能需要比较多个局部最小值以找到一个足够好的解决方案。”
一种方法是监控您的模型在验证数据集上的表现（请参阅这篇文章），当达到所需的验证损失时停止训练。此外，还有各种梯度下降算法的扩展来控制其下坡行为。我建议您在搜索栏中输入梯度下降以查看不同的选项。