在机器学习中分析变量之间的关系时,我们常常发现直线并不能完全解释问题。这时,多项式变换就派上用场了,它能在不增加计算过程复杂性的情况下,为我们的回归模型增加层次。通过将特征转换为它们的多项式形式——平方、立方和其他更高次项——我们赋予了线性模型弯曲和扭转的灵活性,使其能够紧密贴合我们数据的潜在趋势。
这篇博文将探讨我们如何超越简单的线性模型,以捕捉数据中更复杂的关系。您将了解到多项式回归和三次回归技术的强大之处,这些技术能让我们看到表象之外的东西,揭示出直线可能忽略的潜在模式。我们还将深入探讨在增加模型复杂性和保持可预测性之间的平衡,确保模型既强大又实用。
通过我的书《进阶数据科学》启动您的项目。它提供了带有可运行代码的自学教程。
让我们开始吧。

捕捉曲线:多项式回归的高级建模
照片由 Joakim Aglo 拍摄。保留部分权利。
概述
这篇博文分为三部分;它们是:
- 用线性回归建立基准
- 用多项式回归捕捉曲线
- 用三次回归进行实验
用线性回归建立基准
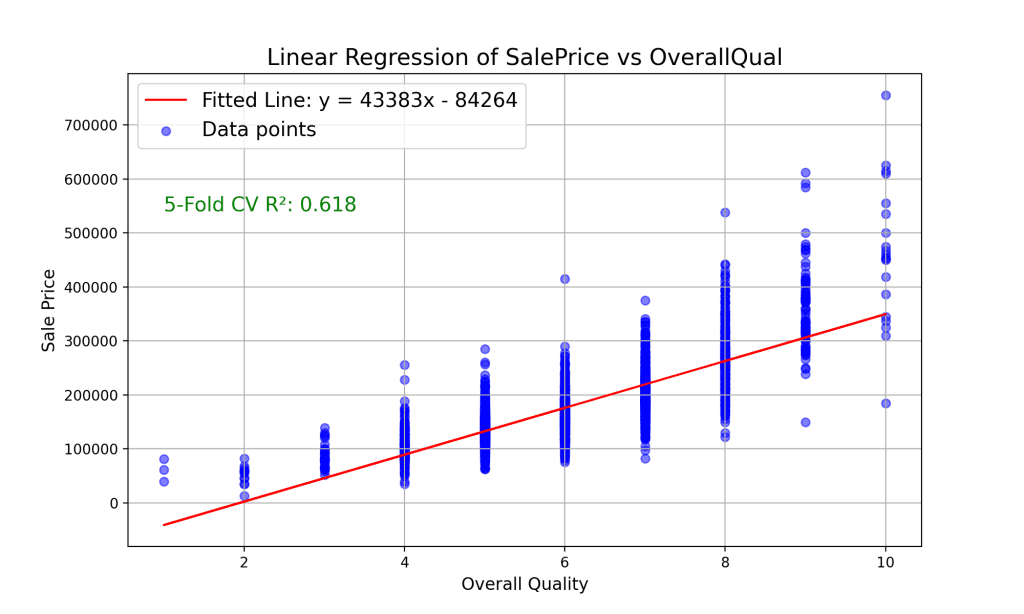
当我们谈论两个变量之间的关系时,线性回归通常是第一步,因为它是最简单的。它通过拟合一条直线来模拟数据之间的关系。这条直线由简单的方程 y = mx + b 描述,其中 y 是因变量,x 是自变量,m 是直线的斜率,b 是 y 轴截距。让我们通过预测 Ames 数据集中基于其“整体质量”(一个从 1 到 10 的整数值)的“销售价格”来演示这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
# 导入必要的库 import pandas as pd 来自 sklearn.linear_model 导入 LinearRegression from sklearn.model_selection import cross_val_score import matplotlib.pyplot as plt # 准备线性回归数据 Ames = pd.read_csv("Ames.csv") X = Ames[["OverallQual"]] # 预测变量 y = Ames["SalePrice"] # 响应变量 # 创建并拟合线性回归模型 linear_model = LinearRegression() linear_model.fit(X, y) # 系数 intercept = int(linear_model.intercept_) slope = int(linear_model.coef_[0]) eqn = f"拟合线: y = {slope}x - {abs(intercept)}" # 执行5折交叉验证以评估模型性能 cv_score = cross_val_score(linear_model, X, y).mean() # 可视化最佳拟合并显示交叉验证结果 plt.figure(figsize=(10, 6)) plt.scatter(X, y, color="blue", alpha=0.5, label="数据点") plt.plot(X, linear_model.predict(X), color="red", label=eqn) plt.title("销售价格 vs 整体质量的线性回归", fontsize=16) plt.xlabel("整体质量", fontsize=12) plt.ylabel("销售价格", fontsize=12) plt.legend(fontsize=14) plt.grid(True) plt.text(1, 540000, f"5折交叉验证 R²: {cv_score:.3f}", fontsize=14, color="green") plt.show() |
通过基本的线性回归,我们的模型得出了以下方程:y = 43383x - 84264。这意味着质量每增加一个点,销售价格大约增加 43,383 美元。为了评估我们模型的性能,我们使用了 5 折交叉验证,得到的 R² 值为 0.618。这个值表明,使用这个简单模型,大约 61.8% 的销售价格变异性可以由房屋的整体质量来解释。
线性回归易于理解和实现。然而,它假设自变量和因变量之间的关系是线性的,这可能并不总是成立,正如上面的散点图所示。虽然线性回归提供了一个很好的起点,但现实世界的数据通常需要更复杂的模型来捕捉曲线关系,我们将在下一节关于多项式回归中看到这一点。
想开始学习进阶数据科学吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
用多项式回归捕捉曲线
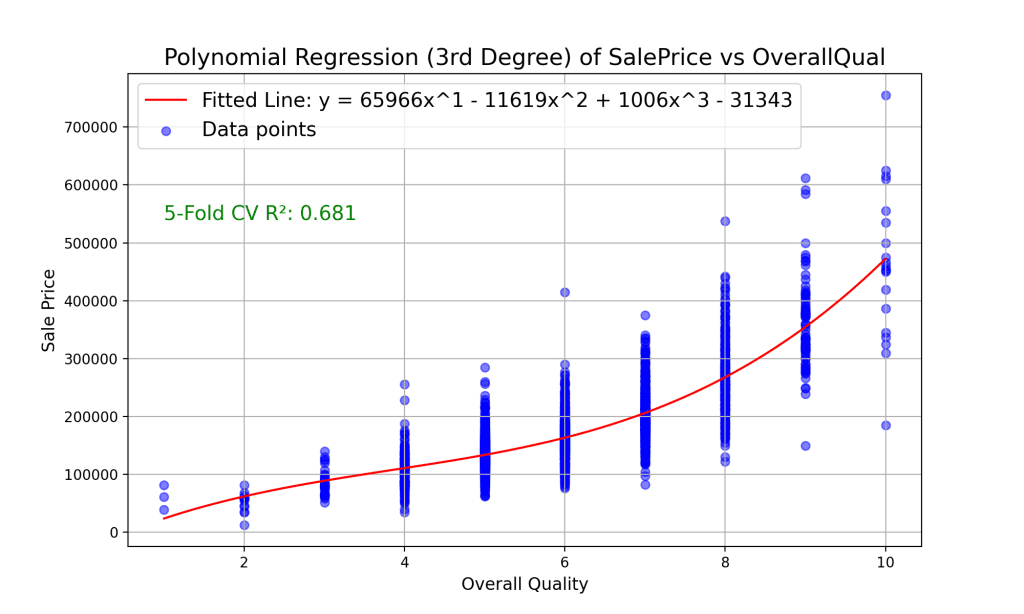
现实世界的关系通常不是直线,而是曲线。多项式回归使我们能够对这些曲线关系进行建模。对于一个三阶多项式,该方法在我们简单的线性方程基础上,为 x 的每个幂次添加项:y = ax + bx^2 + cx^3 + d。我们可以使用 sklearn.preprocessing 库中的 PolynomialFeatures 类来实现这一点,它会生成一个新的特征矩阵,包含所有次数小于或等于指定次数的特征的多项式组合。以下是我们如何将其应用于我们的数据集:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
# 导入必要的库 import pandas as pd import numpy as np 来自 sklearn.linear_model 导入 LinearRegression from sklearn.model_selection import cross_val_score from sklearn.preprocessing import PolynomialFeatures import matplotlib.pyplot as plt # 加载数据 Ames = pd.read_csv("Ames.csv") X = Ames[["OverallQual"]] y = Ames["SalePrice"] # 将预测变量转换为最高3次的多项式特征 poly = PolynomialFeatures(degree=3, include_bias=False) X_poly = poly.fit_transform(X) # 创建并拟合多项式回归模型 poly_model = LinearRegression() poly_model.fit(X_poly, y) # 提取构成多项式方程的模型系数 #intercept = np.rint(poly_model.intercept_).astype(int) intercept = int(poly_model.intercept_) coefs = np.rint(poly_model.coef_).astype(int) eqn = f"拟合线: y = {coefs[0]}x^1 - {abs(coefs[1])}x^2 + {coefs[2]}x^3 - {abs(intercept)}" # 执行 5 折交叉验证 cv_score = cross_val_score(poly_model, X_poly, y).mean() # 生成用于绘制曲线的数据 X_range = np.linspace(X.min(), X.max(), 100).reshape(-1, 1) X_range_poly = poly.transform(X_range) # 绘图 plt.figure(figsize=(10, 6)) plt.scatter(X, y, color="blue", alpha=0.5, label="数据点") plt.plot(X_range, poly_model.predict(X_range_poly), color="red", label=eqn) plt.title("销售价格 vs 整体质量的多项式回归(3次)", fontsize=16) plt.xlabel("整体质量", fontsize=12) plt.ylabel("销售价格", fontsize=12) plt.legend(fontsize=14) plt.grid(True) plt.text(1, 540000, f"5折交叉验证 R²: {cv_score:.3f}", fontsize=14, color="green") plt.show() |
首先,我们将预测变量转换为最高三次的多项式特征。这一增强将我们的特征集从仅仅是 x(整体质量)扩展到了 x, x^2, x^3(即,每个特征变成了三个不同但相关的特征),使得我们的线性模型能够拟合数据中更复杂的曲线关系。然后,我们将这个转换后的数据拟合到一个线性回归模型中,以捕捉整体质量和销售价格之间的非线性关系。
我们的新模型方程为 y = 65966x^1 - 11619x^2 + 1006x^3 - 31343。这条曲线比直线更紧密地拟合数据点,表明这是一个更好的模型。我们的 5 折交叉验证得到的 R² 值为 0.681,比线性模型有所改进。这表明包含平方项和立方项有助于我们的模型捕捉到数据中更多的复杂性。多项式回归引入了拟合曲线的能力,但有时专注于特定的幂次,如立方项,可以揭示更深层次的见解,我们将在三次回归中探讨这一点。
用三次回归进行实验
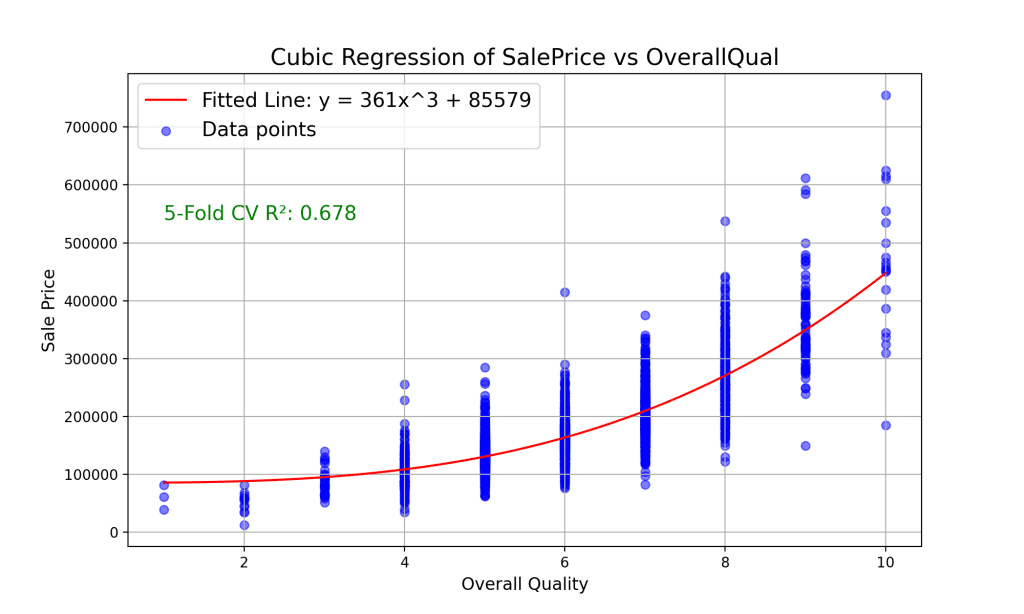
有时,我们可能怀疑 x 的某个特定幂次特别重要。在这种情况下,我们可以专注于该幂次。三次回归是一个特例,我们用自变量的立方来建模关系:y = ax^3 + b。为了有效地专注于这个幂次,我们可以利用 sklearn.preprocessing 库中的 FunctionTransformer 类,它允许我们创建一个自定义转换器来对数据应用特定的函数。这种方法对于分离和突出像 x^3 这样的高次项对响应变量的影响非常有用,清晰地展示了仅立方项如何解释数据中的变异性。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# 导入必要的库 import pandas as pd import numpy as np 来自 sklearn.linear_model 导入 LinearRegression from sklearn.model_selection import cross_val_score from sklearn.preprocessing import FunctionTransformer import matplotlib.pyplot as plt # 加载数据 Ames = pd.read_csv("Ames.csv") X = Ames[["OverallQual"]] y = Ames["SalePrice"] # 应用三次变换的函数 def cubic_transformation(x): return x ** 3 # 应用变换 cubic_transformer = FunctionTransformer(cubic_transformation) X_cubic = cubic_transformer.fit_transform(X) # 拟合模型 cubic_model = LinearRegression() cubic_model.fit(X_cubic, y) # 获取系数和截距 intercept_cubic = int(cubic_model.intercept_) coef_cubic = int(cubic_model.coef_[0]) eqn = f"拟合线: y = {coef_cubic}x^3 + {intercept_cubic}" # 交叉验证 cv_score_cubic = cross_val_score(cubic_model, X_cubic, y).mean() # 生成用于绘制曲线的数据 X_range = np.linspace(X.min(), X.max(), 300) X_range_cubic = cubic_transformer.transform(X_range) # 绘图 plt.figure(figsize=(10, 6)) plt.scatter(X, y, color="blue", alpha=0.5, label="数据点") plt.plot(X_range, cubic_model.predict(X_range_cubic), color="red", label=eqn) plt.title("销售价格 vs 整体质量的三次回归", fontsize=16) plt.xlabel("整体质量", fontsize=12) plt.ylabel("销售价格", fontsize=12) plt.legend(fontsize=14) plt.grid(True) plt.text(1, 540000, f"5折交叉验证 R²: {cv_score_cubic:.3f}", fontsize=14, color="green") plt.show() |
我们对自变量进行了三次变换,并得到了一个三次模型的方程 y = 361x^3 + 85579。这代表了一种比完整多项式回归模型略微简单的方法,仅关注立方项的预测能力。
通过三次回归,我们的 5 折交叉验证得到的 R² 值为 0.678。这个性能略低于完整的多项式模型,但仍然明显优于线性模型。三次回归比更高次的多项式回归更简单,并且可能足以捕捉某些数据集中的关系。它比更高次的多项式模型更不容易过拟合,但比线性模型更灵活。三次回归模型中的系数 361,表示销售价格随着质量立方的增加而增加的速率。这强调了非常高的质量水平对价格的巨大影响,表明质量卓越的房产其销售价格的增长不成比例地更高。这一见解对于专注于高端房产的投资者或开发商尤其有价值,因为在这些房产中,质量是一种溢价。
正如您可能想象的那样,这种技术并不局限于多项式回归。如果您认为在特定场景中有意义,还可以引入更特殊的函数,如对数和指数函数。
进一步阅读
API
教程
- 使用 scikit-learn 在 Python 中进行多项式回归 作者:Tamas Ujhelyi
Ames 住房数据集和数据字典
总结
这篇博文探讨了适用于不同复杂度数据关系建模的各种回归技术。我们从线性回归开始,为基于质量评级预测房价建立了一个基准。本节附带的图表演示了线性模型如何尝试通过数据点拟合一条直线,阐明了回归的基本概念。接着,我们转向多项式回归,处理更复杂、非线性的趋势,这增强了模型的灵活性和准确性。附带的图表显示了多项式曲线如何比简单的线性模型更紧密地拟合数据点。最后,我们专注于三次回归,以检验预测变量特定幂次的影响,分离出高次项对因变量的影响。三次模型被证明特别有效,以足够的精确度和简洁性捕捉了关系的基本特征。
具体来说,你学到了:
- 如何使用可视化技术识别非线性趋势。
- 如何使用多项式回归技术对非线性趋势进行建模。
- 三次回归如何以较低的模型复杂度捕捉到相似的预测能力。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。


暂无评论。