案例研究：预测五年内患糖尿病的几率（第2部分，共3部分）

这是伊戈尔·什瓦尔策（Igor Shvartser）的客座博文，他是一位我一直在指导的聪明的年轻学生。

这篇博文是关于对著名的皮马印第安人糖尿病数据集进行建模的系列文章中的第2部分（更新：可从此处下载）。 在第1部分中，我们定义了问题并研究了数据集，描述了我们在数据中注意到的模式的观察结果。

在本部分中，我们将介绍方法论，进行算法的抽样检查，并回顾初步结果。

通过我的新书 《Weka 机器学习精通》来启动您的项目，书中包含分步教程和所有示例的清晰屏幕截图。

方法论

本研究中的分析和数据处理是使用Weka 机器学习软件完成的。实验使用了十折交叉验证。其工作原理如下：

• 从给定数据中生成 10 个大小相等的子集。
• 将每个子集分为两组：90% 用于训练，10% 用于测试。
• 使用 90% 标记数据中的算法生成一个分类器，并将其应用于第一个子集的 10% 测试数据。
• 对子集 2 到 10 重复此操作。
• 对由 10 个大小相等（训练和测试）的子集生成的 10 个分类器的性能取平均值。

算法

在本研究中，我们将考察 4 种算法的性能。

• 逻辑回归（Cessie & Houwelingen, 1990）
• 朴素贝叶斯（John & Langley, 1995）
• 随机森林（Breiman, 2001）
• C4.5（Quinlan, 1993）

这些算法之所以重要，是因为它们可以对数据集进行分类，能够妥善处理缺失或错误的数据，并且在专注于医学诊断的科学文章中具有一定的意义，请参阅论文《机器学习在医学诊断中的应用：历史、现状与展望》和《人工神经网络在医学诊断中的应用》。

逻辑回归是一种概率统计分类器，用于根据一个或多个预测变量预测分类因变量的结果。该算法衡量因变量与一个或多个自变量之间的关系。

朴素贝叶斯是一种基于贝叶斯定理的简单概率分类器，它做出了强烈的独立性假设。贝叶斯定理如下：

贝叶斯定理

通常，我们可以通过观察某些证据或事件的概率来预测某个事件的结果。我们拥有的支持事件发生的证据越多，我们对其预测的支持就越好。有时，我们拥有的证据可能依赖于其他事件，这会使我们的预测更加复杂。为了创建一个简化的（或“朴素的”）模型，我们假设特定事件的所有证据都与其他事件相互独立。

根据 Breiman 的说法，随机森林创建了投票决定特定结果的树的组合。森林选择获得最多选票的分类。该算法之所以令人兴奋，是因为它是一种装袋算法，并且它有可能通过在不同的训练数据子集上训练算法来提高我们的结果。随机森林学习器的生长方式如下：

• 从训练集中进行有放回抽样，形成输入数据。训练集的三分之一未包含在内，被称为“袋外”（out-of-bag）。
• 为每棵树选择随机数量的属性，这些属性形成节点和叶子。
• 每棵树都生长到尽可能大，而不进行修剪（移除对分类贡献很少的树部分）。
• 然后使用袋外数据来评估每棵树和整个森林的准确性。

C4.5（在 Weka 中也称为“J48”）是一种用于生成分类决策树的算法。C4.5 中的决策树生长方式如下：

1. 在每个节点上，选择最能将样本有效分割成一个类别富集于某个类别而另一个类别贫乏的子集的数据。
2. 设置具有最高信息增益比的属性。
3. 使用此属性创建决策节点并进行预测。

在这种情况下，信息增益比是衡量两个属性的两个概率分布之间差异的度量。该算法对我们有用的原因在于，它解决了 Quinlan 早期算法 ID3 可能遗漏的几个问题。根据 Quinlan 的说法，这些问题包括但不限于：

• 避免对数据过拟合（确定决策树的生长深度）。
• 减误剪枝。
• 规则后剪枝。
• 处理连续属性（例如，温度）。
• 选择合适的属性选择度量。
• 处理具有缺失属性值的训练数据。
• 处理具有不同成本的属性。
• 提高计算效率。

评估 (Evaluation)

在对数据集执行交叉验证后，我将重点通过三个指标来分析这些算法：准确率、ROC 面积和 F1 分数。

根据测试，准确率将确定算法正确分类的实例的百分比。这是我们分析的重要起点，因为它将为我们提供每种算法性能的基准。

ROC 曲线是通过绘制真阳性率与假阳性率绘制而成的。最优分类器的 ROC 面积值接近 1.0，而 0.5 则相当于随机猜测。我相信在这个尺度上看到我们的算法如何进行预测会非常有趣。

最后，F1 分数将是对分类的重要统计分析，因为它将衡量测试准确率。F1 分数使用精确率（真阳性数除以真阳性数和假阳性数之和）和召回率（真阳性数除以真阳性数和假阴性数之和）来输出一个介于 0 和 1 之间的值，值越高表示性能越好。

我强烈认为所有算法的性能会相当相似，因为我们处理的是一个用于分类的小型数据集。然而，这 4 种算法的性能都应该优于类基线预测，后者的准确率约为 65%。

结果

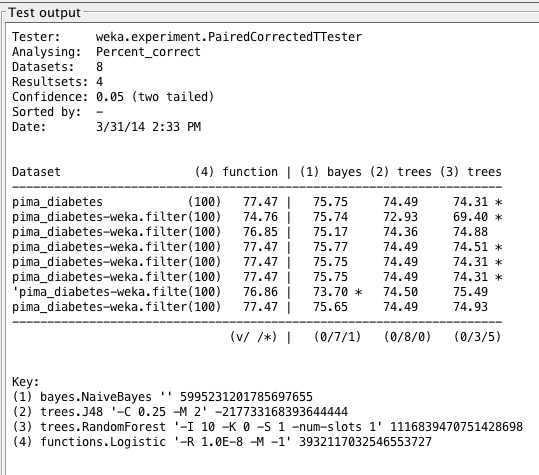
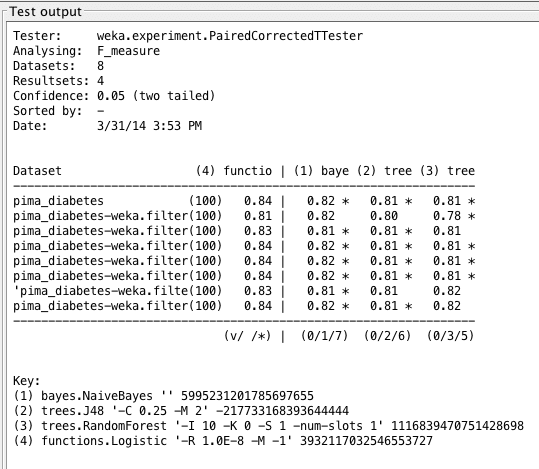
为了对各种算法进行严谨的分析，我使用Weka Experimenter 在所有创建的数据集上评估了性能。结果如下所示。

算法分类准确率在糖尿病数据集上的平均值以及逻辑回归在各种数据集上的性能散点图。

这里的数据表明，逻辑回归在标准、未更改的数据集上表现最好，而随机森林表现最差。然而，任何算法之间都没有明显的赢家。

平均而言，标准化和归一化数据集也似乎能提供更强的准确率，而离散数据集的准确率则最弱。这可能是因为名义值不允许我考虑的算法进行准确预测。

Weka Experimenter 输出比较了逻辑回归与其他算法的性能。

对归一化数据集进行尺度调整可能略微改善了结果。然而，对数据进行转换和重新缩放并未显著改善结果，因此可能并未揭示数据中的任何结构。

我们还可以看到值旁边有星号（*），这些值与第一列（逻辑回归的准确率）中的值在统计学上存在显著差异。Weka 通过配对比较方案来确定统计上的不显著性，这些方案使用标准 T 检验或校正重采样 T 检验，请参阅论文《泛化误差的推断》。

算法 ROC 面积在糖尿病数据集上的平均值以及逻辑回归在各种数据集上的性能散点图。

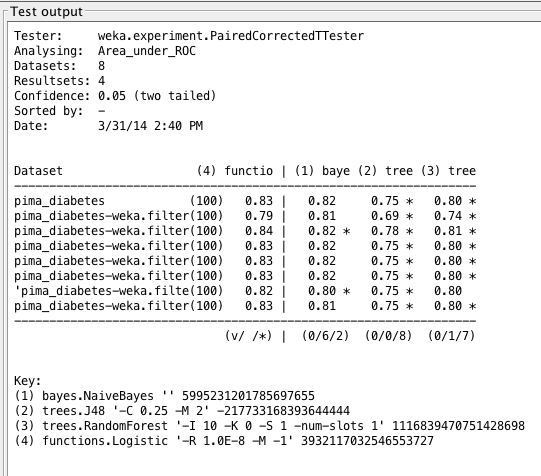
结果再次表明，逻辑回归表现最好，而 C4.5 表现最差。平均而言，纠正了缺失值的数据集表现最好，而离散数据集表现最差。

在这两种情况下，我们发现树形算法在此数据集上的表现不佳。事实上，C4.5 给出的所有结果（以及随机森林中的一个结果）与逻辑回归给出的结果在统计学上存在显著差异。

Weka Experimenter 输出比较了逻辑回归的 ROC 曲线面积与其他算法的 ROC 曲线面积。

这种较差的表现可能是由于树形算法的复杂性。衡量因变量和自变量之间的关系在此可能具有优势。此外，C4.5 可能没有选择正确的属性进行分析，从而导致基于最高信息增益的预测变差。

F1 分数在糖尿病数据集上的值以及逻辑回归 F1 分数在各种数据集上的散点图。

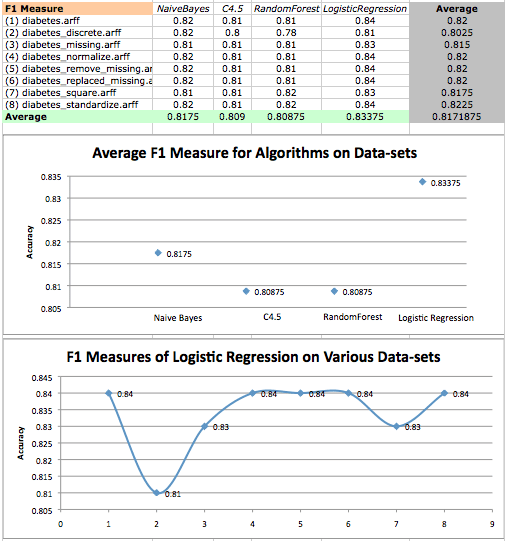
在前两次分析中，我们发现朴素贝叶斯的性能紧随逻辑回归的性能之后。现在我们发现，除了一个结果之外，朴素贝叶斯的所有结果与逻辑回归给出的结果在统计学上都存在显著差异。

Weka Experimenter 输出比较了逻辑回归的 F1 分数与其他算法的 F1 分数。

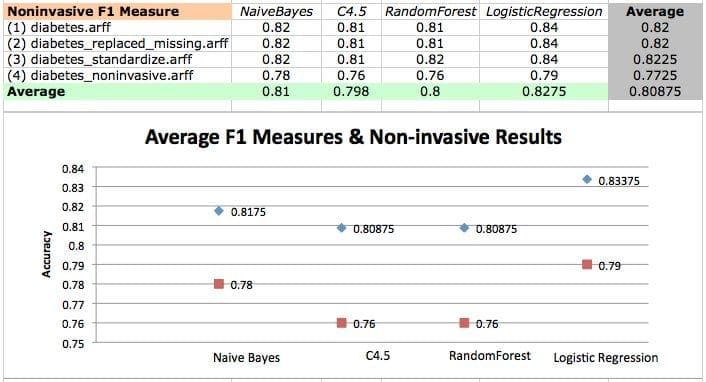
结果表明，逻辑回归表现最好，但差距不大。这意味着逻辑回归在这种情况下具有最准确的测试，并且在此数据集上学习得很好。为了回顾 F1 分数背后的计算，我们知道：

• 召回率： R = TP / (TP + FN)，
• 精确率： P = TP / (TP + FP)，以及
• F1 分数： F1 = 2[ (R * P) / (R + P) ]，

其中 TP = 真阳性，FP = 假阳性，FN = 假阴性。

我们的结果表明，逻辑回归最大化了真阳性率，并最小化了假阴性和假阳性率。至于糟糕的表现，我认为朴素贝叶斯进行的预测过于“朴素”，因此该算法过度使用了独立性假设。

我们可能需要更多数据来为某个事件的发生提供更多证据，这应该能更好地支持其预测。在这种情况下，树形算法可能会因其复杂性而受损，或者仅仅是因为选择了错误的属性进行分析。随着数据集的增大，这可能不再是问题。

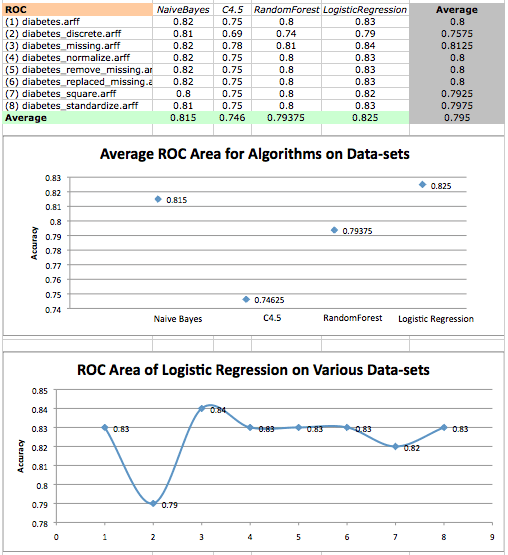
有趣的是，我们还发现表现最好的算法逻辑回归在diabetes_discrete.arff 数据集上表现最差。可以安全地假设，对于逻辑回归而言，除了diabetes_discrete.arff 之外，所有数据转换似乎都能产生更好且非常相似的结果，这一点可以通过每个散点图中相似的趋势清楚地看出！

接下来，在第 3 部分中，我们将研究如何提高分类准确率并最终展示结果。

探索无需代码的机器学习！

在几分钟内开发您自己的模型

...只需几次点击

在我的新电子书中探索如何实现
使用 Weka 精通机器学习

涵盖自学教程和端到端项目，例如
加载数据、可视化、构建模型、调优等等...

最终将机器学习应用到你自己的项目中

跳过学术理论。只看结果。

查看内容