案例研究：预测五年内患糖尿病的风险（第 3 部分，共 3 部分）

这是 Igor Shvartser 的一篇客座文章，他是我指导的一位聪明年轻的学生。

这篇文章是关于著名 Pima 印第安人糖尿病数据集建模的 3 部分系列中的第 3 部分，该系列将探讨分类精度的改进并展示最终结果（更新：可在此处下载）。

在 第 1 部分中，我们定义了问题并研究了数据集，描述了我们从数据中注意到的模式的观察结果。在 第 2 部分中，我们定义了实验方法并展示了初步结果。

通过我的新书 《Weka 机器学习精通》，其中包括分步教程和所有示例的清晰屏幕截图，帮助您启动项目。

改进结果

为了改进结果，我们可以转向提升等集成方法。提升是一种集成方法，它首先使用在训练数据上准备好的基础分类器。然后，在第一个分类器之后创建第二个分类器，以专注于第一个分类器在训练数据中错误分类的实例。

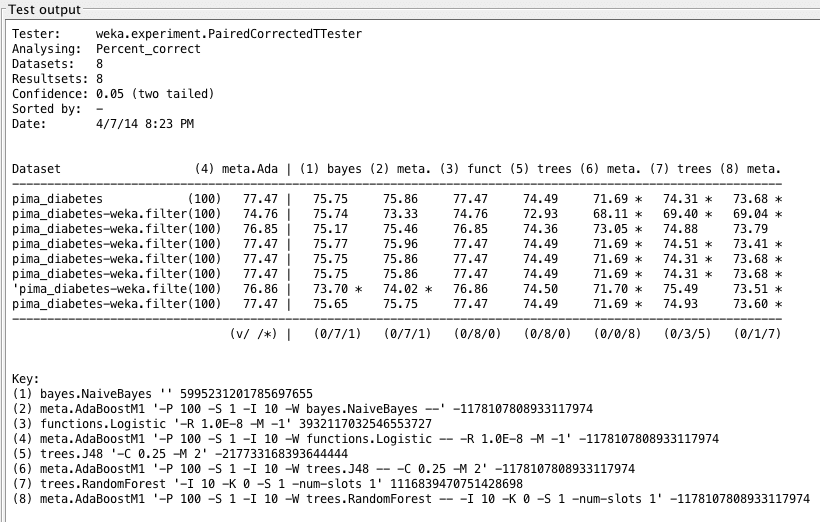
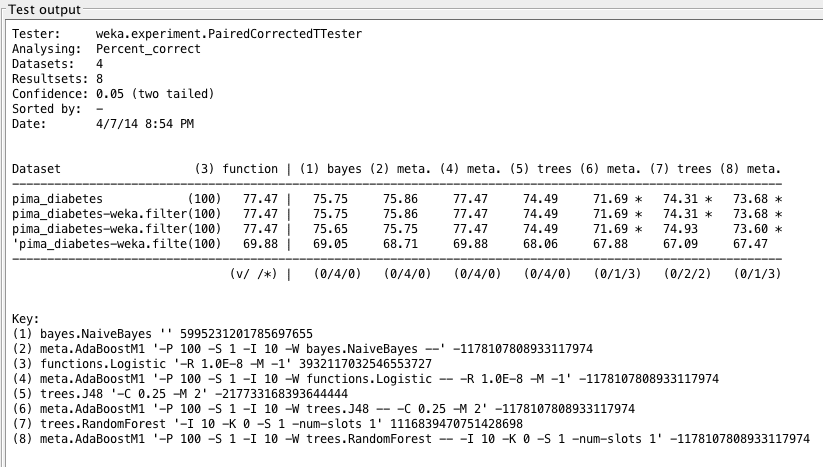
该过程将继续添加分类器，直到达到模型数量或精度的限制。Weka 中的提升是通过 AdaBoostM1（自适应提升）算法提供的。结果如下所示

糖尿病数据集上的提升算法精度平均值，以及逻辑回归在各种数据集上的性能散点图。原始结果为红色，提升结果为蓝色。

很明显，提升对 LogisticRegression 没有影响，但显著降低了树算法的性能。根据 Weka Experimenter 的结果，提升后的 LogisticRegression 的性能与提升后的 C4.5、RandomForest 和提升后的 RandomForest 所给出的结果存在统计学上的显著差异。

由于 RandomForest 已包含集成方法（装袋），因此添加提升可能会导致过拟合，从而解释了性能不佳的原因。

Weka Experimenter 输出比较了提升逻辑回归的性能与其他算法的性能。

无论如何，我们使用性能最佳的算法 LogisticRegression 仍然无法超过 77.47% 的精度。这可能归因于数据限制或交叉验证值较低。我们发现，在某些情况下，例如 C4.5，在执行 AdaBoost 后，精度从 74.28% 急剧下降到 71.4%。

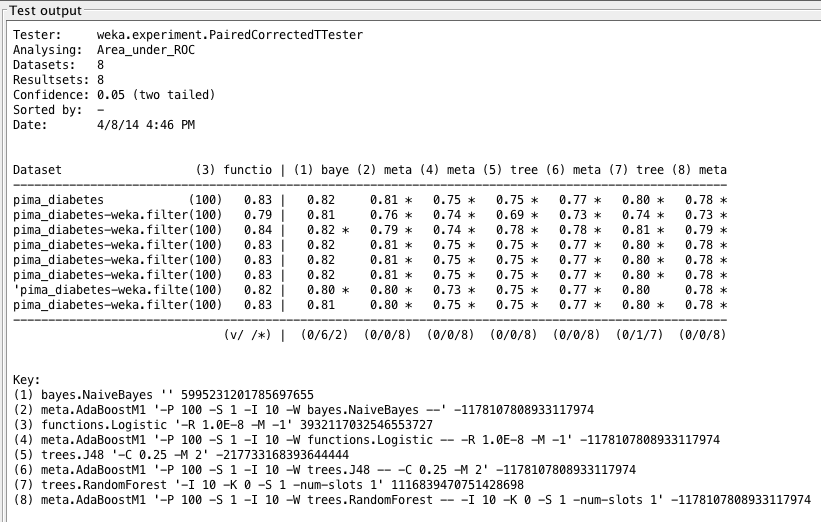
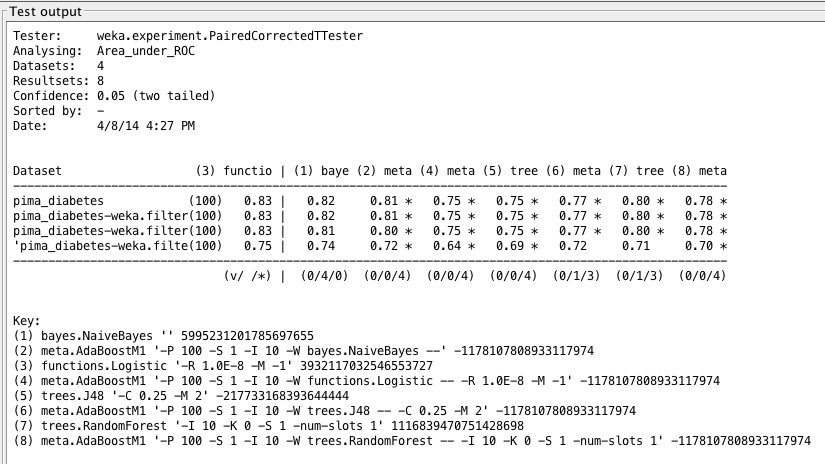
接下来，我们将查看每个提升算法的 ROC 面积。

糖尿病数据集上的提升算法 ROC 面积平均值，以及逻辑回归在各种数据集上的性能散点图。原始结果为红色，提升结果为蓝色。

我们可以看到散点图上的点形成了一个更平滑的趋势。换句话说，数据点之间的方差更小。我们在这里的结果非常有趣：除 C4.5 外，所有提升算法的 ROC 面积值都较小。这意味着与所有其他提升算法相比，提升 C4.5 会产生稍少的假阳性，稍多的真阳性。

Weka Experimenter 输出比较了逻辑回归的 ROC 曲线面积与其他算法的 ROC 曲线面积。

乍一看，这似乎有点奇怪：提升 C4.5 导致精度下降，但 ROC 面积增加。如果考虑到精度实际上是真阳性和假阳性的汇总，而 ROC 面积是命中率和误报率的积分，那么这种差异就很清楚了。无论如何，我们发现提升后的 C4.5 与逻辑回归（默认和提升形式）所给出的结果之间存在统计学上的显著差异。

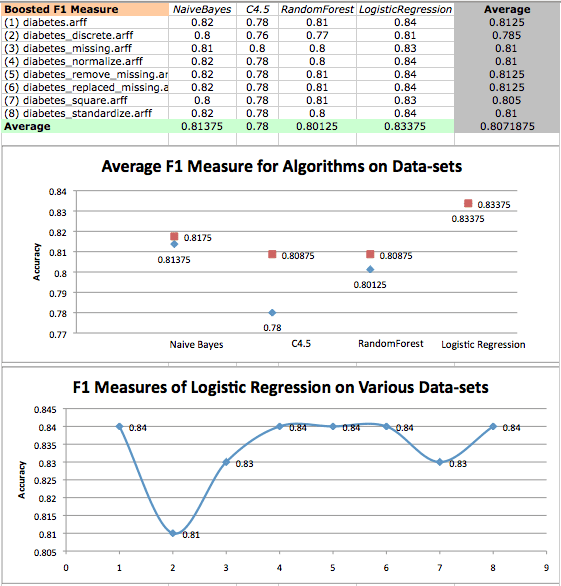
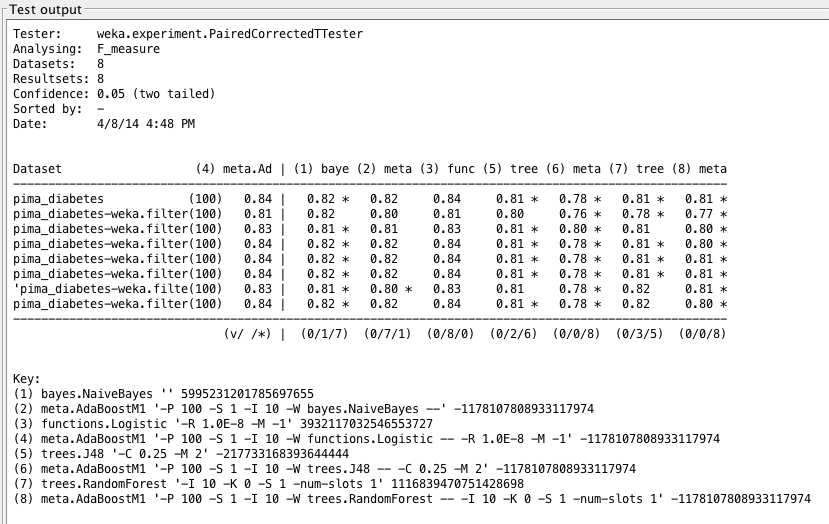
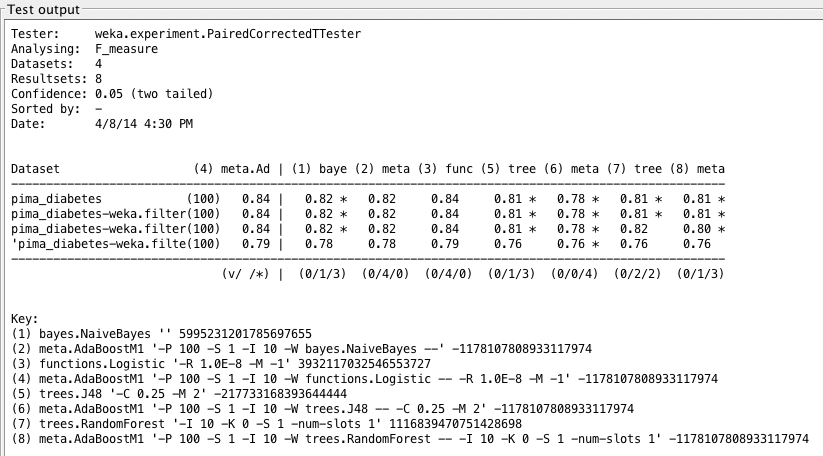
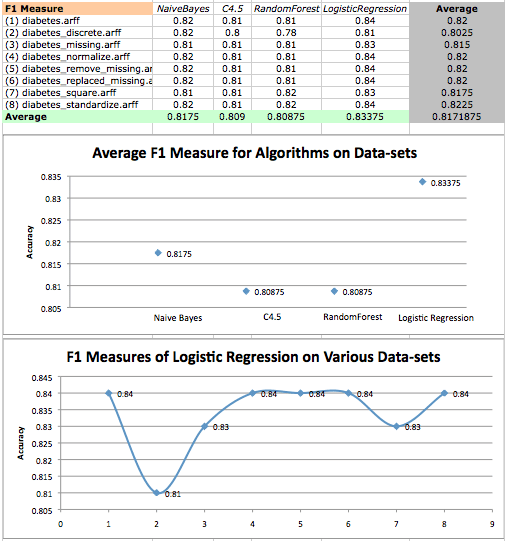
最后，我们将查看提升算法的 F1 指标。

糖尿病数据集上的提升 F1 指标值，以及逻辑回归 F1 指标在各种数据集上的散点图。原始结果为红色，提升结果为蓝色。

同样，我们发现 LogisticRegression 的表现相当不错，但在分析 F1 指标时，提升对 LogisticRegression 没有影响。我们似乎已经触及了 LogisticRegression 的极限，并且再次发现它在统计学上优于树算法。

Weka Experimenter 输出比较了提升逻辑回归的 F1 分数与其他算法的 F1 分数。

移除属性以测试假设

我们可能也有兴趣更改研究以使其无创，因此仅根据四个属性（体重指数、皮肤厚度、年龄和胎龄）来分析算法的性能。这可以帮助医疗专业人员更大规模地进行糖尿病检测，并使检测更快。当然，有了这些优势，我们可能会损失一些精度。

基于我们在数据散点图上看到的情况，我相信我们的算法在该数据集上的表现会相当不错，但不如标准数据集。创建新数据集（并将其命名为 diabetes_noninvasive.arff）是为了测试我们关于糖尿病发病率的假设，即风险随着肥胖和年龄增长而增加。同样，我能够使用 Weka Explorer 移除属性，然后使用 Weka Experimenter 分析算法性能。结果如下所示

侵入性和非侵入性糖尿病数据集上的算法精度平均值。非侵入性结果为红色，原始结果为蓝色。

Weka Experimenter 输出比较了逻辑回归与其他算法的性能。

通过所有指标，正如预测的那样，非侵入性数据集并未提供非常准确的结果。我们发现与早期分析类似的趋势，即 LogisticRegression 仍然是最准确的。

侵入性和非侵入性糖尿病数据集上的算法 ROC 面积平均值。非侵入性结果为红色，原始结果为蓝色。

Weka Experimenter 输出比较了逻辑回归的 ROC 面积与其他算法的 ROC 面积。

我们非侵入性测试的结果实际上与标准数据集的结果相当。我们发现精度的下降可能在长期内代价高昂，但我们可以将此测试用作官方糖尿病检测的前奏。借助当今的技术，可以对在线进行的无创测试来预测糖尿病的发生——只要我们能容忍更多的错误——然后可以建议患者是否需要进一步检测。

侵入性和非侵入性糖尿病数据集上的算法 F1 指标平均值。非侵入性结果为红色，原始结果为蓝色。

Weka Experimenter 输出比较了提升逻辑回归的 F1 指标与其他算法的 F1 指标。

结论

在本研究中，我们比较了各种算法的性能，发现 Logistic Regression 在标准、未经修改的数据集上表现良好。我们试图了解不同修改后的数据集如何影响我们的结果。

此外，我们密切关注了 LogisticRegression，并分析了其在各种指标上的表现。这项工作让我对机器学习在医疗诊断中的应用有了更好的理解。这还是对数据转换和算法分析的一次重要学习。

令人遗憾的是，许多医疗数据集都很小（这可能是由于患者保密性），因为更大的数据集将为我们提供更大的分析灵活性和稳健性。然而，我坚信这项研究是构建帮助诊断患者的方法的一个良好开端，并弥合了医生与大型数据集之间的差距。

探索无需代码的机器学习！

在几分钟内开发您自己的模型

...只需几次点击

在我的新电子书中探索如何实现
使用 Weka 精通机器学习

涵盖自学教程和端到端项目，例如
加载数据、可视化、构建模型、调优等等...

最终将机器学习应用到你自己的项目中

跳过学术理论。只看结果。

查看内容