档案 | 概率

计算学习理论，或称统计学习理论，是指用于量化学习任务和算法的数学框架。这些是机器学习的子领域，机器学习从业者无需深入了解即可在各种问题上取得良好成果。尽管如此，它仍然是一个拥有 […] 的子领域。

贝叶斯定理为计算条件概率提供了一种原则性的方法。它是一个看似简单的计算，为我们直觉常常失灵的场景提供了一种易于使用的方法。培养对贝叶斯定理直觉的最佳方式是思考方程中各项的含义以及 […]

贝叶斯最优分类器是一种概率模型，它为新样本做出最可能的预测。它使用贝叶斯定理进行描述，该定理为计算条件概率提供了原则性的方法。它还与最大后验概率（Maximum a Posteriori, MAP）密切相关，后者是一种寻找 […] 的概率框架。

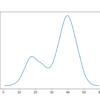
经验分布函数提供了一种为不符合标准概率分布的数据样本建模和采样累积概率的方法。因此，它有时被称为经验累积分布函数，简称ECDF。在本教程中，您将了解经验概率分布函数。完成本教程后，[…]

许多机器学习算法的行为和性能被称为是随机的（stochastic）。随机指的是一个可变过程，其结果包含一些随机性并具有一定的不确定性。它是一个数学术语，与“随机性”（randomness）和“概率性”（probabilistic）密切相关，可以与“确定性”（deterministic）的概念形成对比。这种随机性 […]

密度估计是为来自问题域的观测样本估计概率分布的问题。通常，估计整个分布是难以处理的，因此我们满足于得到分布的期望值，如均值或众数。最大后验概率（Maximum a Posteriori，简称MAP）是一种基于贝叶斯的 […]

概率推断涉及使用概率模型来估计期望值或密度。通常，直接用概率模型推断值是难以处理的，因此必须使用近似方法。马尔可夫链蒙特卡罗采样提供了一类算法，用于从高维概率分布中进行系统性随机抽样。与蒙特卡罗采样方法不同，后者 […]

蒙特卡罗方法是一类用于随机抽样概率分布的技术。在许多问题领域中，描述或估计概率分布相对直接，但计算所需量却是难以处理的。这可能是由于多种原因，例如领域的随机性或指数级的 […]

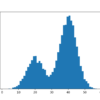
最大似然估计是一种通过搜索概率分布及其参数来对数据集进行密度估计的方法。它是一种通用且有效的方法，是许多机器学习算法的基础，但它要求训练数据集是完整的，例如，所有相关的交互随机变量都存在。如果 […]，最大似然估计将变得难以处理。

模型选择是从一组候选模型中选择一个的问题。通常的做法是选择在保留的测试数据集上表现最好的模型，或者使用重采样技术（如k折交叉验证）来估计模型性能。另一种模型选择方法涉及使用概率统计度量 […]