用于机器学习的分类和回归树

决策树是预测建模机器学习中一种重要的算法。

经典的决策树算法已经存在了几十年，像随机森林这样的现代变种是现有的最强大的技术之一。

在这篇文章中，您将发现这种简单的决策树算法，它以更现代的名称 CART 而闻名，CART 代表分类与回归树。阅读本文后，您将了解

• 用于描述机器学习中 CART 算法的许多名称。
• 学习到的 CART 模型使用的表示，它实际上存储在磁盘上。
• 如何从训练数据中学习 CART 模型。
• 如何使用学习到的 CART 模型对未见过的数据进行预测。
• 可用于进一步了解 CART 和相关算法的其他资源。

如果您上过算法和数据结构课程，您可能很难克制自己不去实现这个简单而强大的算法。从那里，您离自己实现随机森林只差一小步。

通过我的新书《掌握机器学习算法》启动您的项目，包括所有示例的分步教程和Excel 电子表格文件。

让我们开始吧。

• 2017 年 8 月更新：修复了一个排版错误，该错误指出基尼系数是类实例的数量，应该是实例的比例。还更新了内容，以展示用于评估分割的基尼加权以及计算子节点的纯度。

用于机器学习的分类和回归树
照片由 Wonderlane 提供，保留部分权利。

决策树

分类与回归树，简称 CART，是由 Leo Breiman 引入的术语，用于指代可用于分类或回归预测建模问题的 决策树 算法。

传统上，这种算法被称为“决策树”，但在某些平台（如 R）上，它们被称作更现代的术语 CART。

CART 算法为袋装决策树、随机森林和梯度提升决策树等重要算法提供了基础。

获取您的免费算法思维导图

方便的机器学习算法思维导图样本。

我创建了一份方便的思维导图，其中包含60多种按类型组织的算法。

下载、打印并使用它。

CART 模型表示

CART 模型的表示是一个二叉树。

这是您在算法和数据结构中遇到的二叉树，没什么特别的。每个根节点代表一个输入变量 (x) 和该变量上的一个分割点（假设变量是数值型的）。

树的叶节点包含一个用于进行预测的输出变量 (y)。

给定一个包含两个输入（x），身高（厘米）和体重（公斤），输出性别（男或女）的数据集，下面是一个二叉决策树的粗略示例（纯属虚构，仅用于演示目的）。

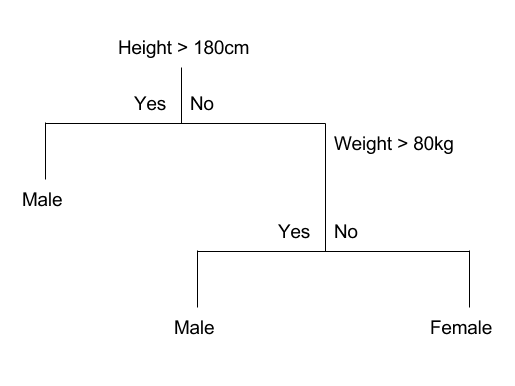
决策树示例

该树可以作为图形或一组规则存储到文件中。例如，下面是上述决策树的一组规则。

通过上述 CART 模型的二叉树表示，进行预测相对简单。

给定一个新的输入，通过评估从树的根节点开始的特定输入来遍历树。

一个学习到的二叉树实际上是对输入空间的划分。您可以将每个输入变量视为 p 维空间中的一个维度。决策树将其划分为矩形（当 p=2 个输入变量时）或具有更多输入的一些超矩形。

新数据通过树进行过滤并落在其中一个矩形中，该矩形的输出值就是模型做出的预测。这让您对 CART 模型能够做出的决策类型有所了解，例如箱形决策边界。

例如，给定输入 [身高 = 160 厘米，体重 = 65 公斤]，我们将按如下方式遍历上述树：

从数据中学习 CART 模型

创建 CART 模型涉及选择输入变量和这些变量上的分割点，直到构建出合适的树。

使用贪婪算法选择要使用的输入变量和特定的分割点，以最小化成本函数。树的构建使用预定义的停止准则结束，例如分配给树的每个叶节点的训练实例的最小数量。

贪婪分割

创建二叉决策树实际上是一个划分输入空间的过程。采用一种称为 递归二叉分割 的贪婪方法来划分空间。

这是一个数值过程，其中所有值都被排列起来，并使用成本函数尝试和测试不同的分割点。选择成本最低的分割点（因为我们最小化成本）。

所有输入变量和所有可能的分割点都以贪婪的方式进行评估和选择（例如，每次都选择最佳分割点）。

对于回归预测建模问题，用于选择分割点并最小化的成本函数是所有落入矩形内的训练样本的平方误差和

和(y - 预测)^2

其中 y 是训练样本的输出，prediction 是矩形的预测输出。

对于分类，使用基尼指数函数，该函数提供了叶节点“纯度”的指示（分配给每个节点的训练数据的混合程度）。

G = sum(pk * (1 – pk))

其中 G 是所有类的基尼指数，pk 是感兴趣矩形中具有类 k 的训练实例的比例。一个所有类都属于同一类型（完美类纯度）的节点将具有 G=0，而对于二元分类问题，具有 50-50 类分割（最差纯度）的节点将具有 G=0.5。

对于二元分类问题，可以将其改写为

G = 2 * p1 * p2
或者
G = 1 – (p1^2 + p2^2)

每个节点的基尼指数计算按父节点中的总实例数加权。因此，二元分类问题中选定分割点的基尼分数计算如下：

G = ((1 – (g1_1^2 + g1_2^2)) * (ng1/n)) + ((1 – (g2_1^2 + g2_2^2)) * (ng2/n))

其中 G 是分割点的基尼指数，g1_1 是组 1 中类别 1 的实例比例，g1_2 是类别 2 的实例比例，g2_1 是组 2 中类别 1 的实例比例，g2_2 是组 2 中类别 2 的实例比例，ng1 和 ng2 是组 1 和组 2 中的实例总数，n 是我们试图从父节点中分组的实例总数。

停止准则

上述递归二叉分割过程需要知道何时停止分割，因为它使用训练数据向下遍历树。

最常见的停止过程是使用分配给每个叶节点的训练实例数量的最小计数。如果计数小于某个最小值，则不接受分割，并将该节点视为最终叶节点。

训练成员的数量根据数据集进行调整，例如 5 或 10。它定义了树对训练数据的特异性。如果过于具体（例如计数为 1），树将过度拟合训练数据，并且在测试集上可能表现不佳。

修剪树

停止准则很重要，因为它强烈影响树的性能。您可以在学习树后使用 修剪 来进一步提升性能。

决策树的复杂性定义为树中分割的数量。更简单的树是首选。它们易于理解（您可以打印出来并展示给领域专家），并且不太可能过度拟合您的数据。

最快和最简单的修剪方法是遍历树中的每个叶节点，并使用保留测试集评估移除它的效果。仅当移除叶节点导致整个测试集上的总成本函数下降时才移除叶节点。当无法进一步改进时，停止移除节点。

可以使用更复杂的修剪方法，例如成本复杂性修剪（也称为最弱链接修剪），其中使用学习参数（alpha）来权衡是否可以根据子树的大小移除节点。

决策树的递归二叉分割
照片由 Paul L Dineen 拍摄，保留部分权利。

CART 的数据准备

CART 不需要任何特殊的数据准备，只需对问题进行良好表示即可。

进一步阅读

本节列出了一些资源，如果您想深入了解 CART，可以参考这些资源。

• 分类与回归树

以下是一些从机器学习角度描述 CART 算法的优秀机器学习书籍。

• 统计学习导论：附带 R 应用程序，第八章
• 应用预测建模，第八章和第十四章
• 数据挖掘：实用机器学习工具和技术，第六章。

总结

在这篇文章中，您发现了机器学习中的分类与回归树 (CART)。您了解了

• 该算法的经典名称“决策树”和更现代的名称“CART”。
• CART 使用的表示是二叉树。
• 通过给定新的输入记录遍历二叉树，CART 可以进行预测。
• 树是使用训练数据上的贪婪算法学习的，以选择树中的分割点。
• 停止准则定义了树学习的程度，并且可以使用修剪来改进学习到的树。

您对 CART 或本文有任何疑问吗？
在评论中提问，我将尽力回答。

了解机器学习算法的工作原理！

几分钟内了解算法如何工作

...只需算术和简单示例

在我的新电子书中探索如何实现
精通机器学习算法

它涵盖了**10种顶级算法**的**解释**和**示例**，例如：
_线性回归_、_k-近邻_、_支持向量机_等等...

最后，揭开
机器学习算法的神秘面纱

跳过学术理论。只看结果。

查看内容