分类是一种预测建模问题,涉及为给定的输入数据样本分配一个标签。
分类预测建模问题可以被构建为计算给定数据样本下类别标签的条件概率。贝叶斯定理为计算这种条件概率提供了一种有原则的方法,尽管在实践中需要大量的样本(非常大的数据集)并且计算成本高昂。
相反,可以通过做一些假设来简化贝叶斯定理的计算,例如假设每个输入变量都独立于所有其他输入变量。虽然这是一个戏剧性且不切实际的假设,但这使得条件概率的计算变得易于处理,并产生了一种称为朴素贝叶斯的有效分类模型。
在本教程中,您将了解用于分类预测建模的朴素贝叶斯算法。
完成本教程后,您将了解:
- 如何将分类预测建模构建为条件概率模型。
- 如何使用贝叶斯定理解决分类的条件概率模型。
- 如何实现简化的贝叶斯定理进行分类,即朴素贝叶斯算法。
通过我的新书《机器学习概率论》启动您的项目,其中包括所有示例的分步教程和 Python 源代码文件。
让我们开始吧。
- 2019年10月更新:修复了数学符号中的微小不一致问题。
- **2020年1月更新**:已针对 scikit-learn v0.22 API 的变更进行更新。

如何在 Python 中从零开始开发朴素贝叶斯分类器
照片由 Ryan Dickey 拍摄,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 分类的条件概率模型
- 简化或朴素贝叶斯
- 如何计算先验概率和条件概率
- 朴素贝叶斯的工作示例
- 使用朴素贝叶斯时的5个技巧
分类的条件概率模型
在机器学习中,我们通常对预测建模问题感兴趣,即我们希望为给定的观测值预测一个类别标签。例如,根据花的测量值对植物物种进行分类。
这类问题被称为分类预测建模问题,与涉及预测数值的回归问题相对。模型的观察值或输入称为 X,模型的类别标签或输出称为 y。
X 和 y 共同代表从领域中收集的观测数据,即用于拟合模型的训练数据表格或矩阵(列和行,或特征和样本)。模型必须学习如何将特定示例映射到类别标签,即 y = f(X),以最小化分类错误的误差。
解决此问题的一种方法是开发一个概率模型。从概率的角度来看,我们感兴趣的是估计给定观测值下类别标签的条件概率。
例如,一个分类问题可能有 k 个类别标签 y1, y2, …, yk 和 n 个输入变量 X1, X2, …, Xn。我们可以为给定实例或每列的一组输入值 x1, x2, …, xn 计算类别标签的条件概率,如下所示:
- P(yi | x1, x2, …, xn)
然后可以为问题中的每个类别标签计算条件概率,并将具有最高概率的标签作为最可能的分类返回。
条件概率可以使用联合概率计算,但这将是难以处理的。贝叶斯定理为计算条件概率提供了一种有原则的方法。
贝叶斯定理计算的简单形式如下:
- P(A|B) = P(B|A) * P(A) / P(B)
其中我们感兴趣计算的概率 P(A|B) 称为后验概率,事件 P(A) 的边缘概率称为先验概率。
我们可以使用贝叶斯定理将分类问题构建为条件分类问题,如下所示:
- P(yi | x1, x2, …, xn) = P(x1, x2, …, xn | yi) * P(yi) / P(x1, x2, …, xn)
先验概率 P(yi) 很容易从数据集中估计,但是基于类别的观测条件概率 P(x1, x2, …, xn | yi) 是不可行的,除非示例数量非常大,例如,大到足以有效地估计所有不同可能值组合的概率分布。
因此,贝叶斯定理的直接应用也变得难以处理,特别是随着变量或特征(n)数量的增加。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
简化或朴素贝叶斯
使用贝叶斯定理进行条件概率分类模型的解决方案是简化计算。
贝叶斯定理假设每个输入变量都依赖于所有其他变量。这是计算复杂性的一个原因。我们可以去掉这个假设,并认为每个输入变量都彼此独立。
这将模型从一个依赖的条件概率模型改变为一个独立的条件概率模型,并极大地简化了计算。
首先,从计算中移除分母 P(x1, x2, …, xn),因为它是在计算给定实例的每个类别的条件概率时使用的一个常数,其作用是归一化结果。
- P(yi | x1, x2, …, xn) = P(x1, x2, …, xn | yi) * P(yi)
接下来,给定类别标签的所有变量的条件概率被改变为给定类别标签的每个变量值的单独条件概率。然后将这些独立的条件变量相乘。例如:
- P(yi | x1, x2, …, xn) = P(x1|yi) * P(x2|yi) * … P(xn|yi) * P(yi)
可以为每个类别标签执行此计算,并选择具有最大概率的标签作为给定实例的分类。这个决策规则被称为最大后验概率(MAP)决策规则。
这种对贝叶斯定理的简化是常见的,并广泛用于分类预测建模问题,通常被称为朴素贝叶斯。
“naive” 这个词是法语,通常在“i”上有一个分音符(umlaut),为了简单起见通常会省略,而“Bayes”大写是因为它以托马斯·贝叶斯牧师的名字命名。
如何计算先验概率和条件概率
现在我们知道了什么是朴素贝叶斯,我们可以更仔细地看看如何计算方程中的元素。
先验概率 P(yi) 的计算很简单。可以通过将训练数据集中具有该类别标签的观测频率除以训练数据集中的总示例数(行数)来估计。例如:
- P(yi) = 具有 yi 的示例数 / 总示例数
给定类别标签的特征值的条件概率也可以从数据中估计。具体来说,是那些属于给定类别的数据示例,并且每个变量对应一个数据分布。这意味着如果有 K 个类别和 n 个变量,那么必须创建和维护 k * n 个不同的概率分布。
根据每个特征的数据类型,需要采用不同的方法。具体来说,数据用于估计三种标准概率分布之一的参数。
对于分类变量,如计数或标签,可以使用多项分布。如果变量是二元的,如是/否或真/假,可以使用二项分布。如果变量是数值型的,如测量值,通常使用高斯分布。
- 二元:二项分布。
- 分类:多项分布。
- 数值:高斯分布。
这三种分布非常常见,以至于朴素贝叶斯的实现通常以分布命名。例如:
- 二项朴素贝叶斯:使用二项分布的朴素贝叶斯。
- 多项朴素贝叶斯:使用多项分布的朴素贝叶斯。
- 高斯朴素贝叶斯:使用高斯分布的朴素贝叶斯。
输入变量数据类型混合的数据集可能需要为每个变量选择不同类型的数据分布。
使用三种常见分布之一不是强制性的;例如,如果已知一个实值变量具有不同的特定分布,如指数分布,那么可以使用该特定分布。如果一个实值变量没有明确定义的分布,如双峰或多峰分布,那么可以使用核密度估计器来估计概率分布。
朴素贝叶斯算法已被证明是有效的,因此在文本分类任务中很受欢迎。文档中的单词可以编码为二元(单词存在)、计数(单词出现次数)或频率(tf/idf)输入向量,并分别使用二元、多项或高斯概率分布。
朴素贝叶斯的工作示例
在本节中,我们将通过一个机器学习数据集上的小例子来具体说明朴素贝叶斯的计算。
我们可以使用 scikit-learn API 中的 make_blobs() 函数生成一个小的、人为构造的二元(2类)分类问题。
下面的示例生成了 100 个具有两个数值输入变量的示例,每个示例被分配到两个类别之一。
|
1 2 3 4 5 6 7 8 |
# 生成小型分类数据集的示例 from sklearn.datasets import make_blobs # 生成二维分类数据集 X, y = make_blobs(n_samples=100, centers=2, n_features=2, random_state=1) # 总结 print(X.shape, y.shape) print(X[:5]) print(y[:5]) |
运行该示例会生成数据集并总结其大小,确认数据集已按预期生成。
“random_state”参数设置为 1,确保每次运行代码时都会生成相同的随机观测样本。
前五个示例的输入和输出元素也被打印出来,显示两个输入变量确实是数值型的,并且每个示例的类别标签是 0 或 1。
|
1 2 3 4 5 6 7 |
(100, 2) (100,) [[-10.6105446 4.11045368] [ 9.05798365 0.99701708] [ 8.705727 1.36332954] [ -8.29324753 2.35371596] [ 6.5954554 2.4247682 ]] [0 1 1 0 1] |
我们将使用高斯概率分布来建模数值输入变量。
这可以通过使用 norm SciPy API 来实现。首先,可以通过指定分布的参数(例如均值和标准差)来构建分布,然后可以使用 norm.pdf() 函数对特定值进行概率密度函数采样。
我们可以使用 mean() 和 std() NumPy 函数从数据集中估计分布的参数。
下面的 fit_distribution() 函数接受一个变量的数据样本并拟合一个数据分布。
|
1 2 3 4 5 6 7 8 9 |
# 对单变量数据样本拟合概率分布 def fit_distribution(data): # 估计参数 mu = mean(data) sigma = std(data) print(mu, sigma) # 拟合分布 dist = norm(mu, sigma) return dist |
回想一下,我们感兴趣的是每个输入变量的条件概率。这意味着我们需要为每个输入变量建立一个分布,并为每个类别标签建立一组分布,总共四个分布。
首先,我们必须将数据按每个类别标签分成不同的样本组。
|
1 2 3 4 5 |
... # 将数据按类别排序 Xy0 = X[y == 0] Xy1 = X[y == 1] print(Xy0.shape, Xy1.shape) |
然后我们可以使用这些组来计算一个数据样本属于每个组的先验概率。
由于我们在两个类别中创建了相同数量的示例,这个概率将恰好是50%;尽管如此,为了完整性,我们还是会计算这些先验概率。
|
1 2 3 4 5 |
... # 计算先验概率 priory0 = len(Xy0) / len(X) priory1 = len(Xy1) / len(X) print(priory0, priory1) |
最后,我们可以调用我们定义的 fit_distribution() 函数,为每个类别标签的每个变量准备一个概率分布。
|
1 2 3 4 5 6 7 |
... # 为 y==0 创建概率密度函数 (PDFs) X1y0 = fit_distribution(Xy0[:, 0]) X2y0 = fit_distribution(Xy0[:, 1]) # 为 y==1 创建概率密度函数 (PDFs) X1y1 = fit_distribution(Xy1[:, 0]) X2y1 = fit_distribution(Xy1[:, 1]) |
将所有这些整合在一起,下面列出了该数据集的完整概率模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 总结数据集的概率分布 from sklearn.datasets import make_blobs from scipy.stats import norm from numpy import mean from numpy import std # 对单变量数据样本拟合概率分布 def fit_distribution(data): # 估计参数 mu = mean(data) sigma = std(data) print(mu, sigma) # 拟合分布 dist = norm(mu, sigma) return dist # 生成二维分类数据集 X, y = make_blobs(n_samples=100, centers=2, n_features=2, random_state=1) # 将数据按类别排序 Xy0 = X[y == 0] Xy1 = X[y == 1] print(Xy0.shape, Xy1.shape) # 计算先验概率 priory0 = len(Xy0) / len(X) priory1 = len(Xy1) / len(X) print(priory0, priory1) # 为 y==0 创建概率密度函数 (PDFs) X1y0 = fit_distribution(Xy0[:, 0]) X2y0 = fit_distribution(Xy0[:, 1]) # 为 y==1 创建概率密度函数 (PDFs) X1y1 = fit_distribution(Xy1[:, 0]) X2y1 = fit_distribution(Xy1[:, 1]) |
运行该示例首先将数据集按两个类别标签分成两组,并确认每组的大小相等,先验概率为50%。
然后为每个类别标签的每个变量准备概率分布,并报告每个分布的均值和标准差参数,确认分布是不同的。
|
1 2 3 4 5 6 |
(50, 2) (50, 2) 0.5 0.5 -1.5632888906409914 0.787444265443213 4.426680361487157 0.958296071258367 -9.681177100524485 0.8943078901048118 -3.9713794295185845 0.9308177595208521 |
接下来,我们可以使用准备好的概率模型进行预测。
每个类别标签的独立条件概率可以通过使用该类别的先验概率(50%)和每个变量值的条件概率来计算。
下面的 probability() 函数为一个输入示例(一个包含两个值的数组)执行此计算,给定每个变量的先验概率和条件概率分布。返回的值是一个分数而不是一个概率,因为这个量没有被归一化,这是实现朴素贝叶斯时经常做的简化。
|
1 2 3 |
# 计算独立条件概率 def probability(X, prior, dist1, dist2): return prior * dist1.pdf(X[0]) * dist2.pdf(X[1]) |
我们可以使用这个函数来计算一个示例属于每个类别的概率。
首先,我们可以选择一个要分类的示例;在这种情况下,是数据集中的第一个示例。
|
1 2 3 |
... # 分类一个示例 Xsample, ysample = X[0], y[0] |
接下来,我们可以计算该示例属于第一类的分数,然后是第二类,然后报告结果。
|
1 2 3 4 5 |
... py0 = probability(Xsample, priory0, distX1y0, distX2y0) py1 = probability(Xsample, priory1, distX1y1, distX2y1) print('P(y=0 | %s) = %.3f' % (Xsample, py0*100)) print('P(y=1 | %s) = %.3f' % (Xsample, py1*100)) |
分数最高的类别将是最终的分类结果。
将这些内容整合在一起,下面列出了拟合朴素贝叶斯模型并用其进行一次预测的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# 使用朴素贝叶斯模型准备和进行预测的示例 from sklearn.datasets import make_blobs from scipy.stats import norm from numpy import mean from numpy import std # 对单变量数据样本拟合概率分布 def fit_distribution(data): # 估计参数 mu = mean(data) sigma = std(data) print(mu, sigma) # 拟合分布 dist = norm(mu, sigma) return dist # 计算独立条件概率 def probability(X, prior, dist1, dist2): return prior * dist1.pdf(X[0]) * dist2.pdf(X[1]) # 生成二维分类数据集 X, y = make_blobs(n_samples=100, centers=2, n_features=2, random_state=1) # 将数据按类别排序 Xy0 = X[y == 0] Xy1 = X[y == 1] # 计算先验概率 priory0 = len(Xy0) / len(X) priory1 = len(Xy1) / len(X) # 为 y==0 创建概率密度函数 (PDFs) distX1y0 = fit_distribution(Xy0[:, 0]) distX2y0 = fit_distribution(Xy0[:, 1]) # 为 y==1 创建概率密度函数 (PDFs) distX1y1 = fit_distribution(Xy1[:, 0]) distX2y1 = fit_distribution(Xy1[:, 1]) # 分类一个示例 Xsample, ysample = X[0], y[0] py0 = probability(Xsample, priory0, distX1y0, distX2y0) py1 = probability(Xsample, priory1, distX1y1, distX2y1) print('P(y=0 | %s) = %.3f' % (Xsample, py0*100)) print('P(y=1 | %s) = %.3f' % (Xsample, py1*100)) print('真实值:y=%d' % ysample) |
运行该示例首先如前所述准备先验概率和条件概率,然后用它们对一个示例进行预测。
该示例属于 y=0 的分数约为 0.3(请记住这是一个未归一化的概率),而该示例属于 y=1 的分数为 0.0。因此,我们会将该示例分类为属于 y=0。
在这种情况下,已知真实或实际的结果是 y=0,这与我们的朴素贝叶斯模型的预测相符。
|
1 2 3 |
P(y=0 | [-0.79415228 2.10495117]) = 0.348 P(y=1 | [-0.79415228 2.10495117]) = 0.000 真实值: y=0 |
在实践中,使用朴素贝叶斯算法的优化实现是一个好主意。scikit-learn 库提供了三种实现,每种实现对应三种主要概率分布之一;例如,BernoulliNB、MultinomialNB 和 GaussianNB 分别用于二项分布、多项分布和高斯分布的输入变量。
要使用 scikit-learn 朴素贝叶斯模型,首先定义模型,然后在训练数据集上进行拟合。拟合后,可以通过 predict_proba() 函数预测概率,也可以通过 predict() 函数直接预测类别标签。
下面列出了在同一测试数据集上拟合高斯朴素贝叶斯模型(GaussianNB)的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 高斯朴素贝叶斯示例 from sklearn.datasets import make_blobs from sklearn.naive_bayes import GaussianNB # 生成二维分类数据集 X, y = make_blobs(n_samples=100, centers=2, n_features=2, random_state=1) # 定义模型 model = GaussianNB() # 拟合模型 model.fit(X, y) # 选择单个样本 Xsample, ysample = [X[0]], y[0] # 进行概率预测 yhat_prob = model.predict_proba(Xsample) print('预测概率: ', yhat_prob) # 进行分类预测 yhat_class = model.predict(Xsample) print('预测类别: ', yhat_class) print('真实值:y=%d' % ysample) |
运行该示例会在训练数据集上拟合模型,然后对我们在前一个示例中使用的同一个第一个示例进行预测。
在这种情况下,该示例属于 y=0 的概率是 1.0,即确定无疑。y=1 的概率是一个非常接近 0.0 的小值。
最后,直接预测了类别标签,再次与该示例的真实情况相匹配。
|
1 2 3 |
预测概率: [[1.00000000e+00 5.52387327e-30]] 预测类别: [0] 真实值: y=0 |
使用朴素贝叶斯时的5个技巧
本节列出了一些在使用朴素贝叶斯模型时的实用技巧。
1. 对复杂分布使用核密度估计(KDE)
如果一个变量的概率分布复杂或未知,使用核密度估计器(KDE)直接从数据样本中近似分布会是一个好主意。
一个很好的例子是高斯核密度估计。
2. 随着变量依赖性增加,性能下降
根据定义,朴素贝叶斯假设输入变量彼此独立。
这在大多数情况下都表现良好,即使某些或大部分变量实际上是相关的。然而,输入变量的依赖性越强,算法的性能就越差。
3. 使用对数避免数值下溢
计算一个示例对一个类别标签的独立条件概率涉及到将多个概率相乘,一个是该类别的概率,每个输入变量各一个。因此,将许多小数相乘可能会导致数值不稳定,特别是当输入变量数量增加时。
为了克服这个问题,通常将概率的乘积计算转换为对数概率的和。例如:
- P(yi | x1, x2, …, xn) = log(P(x1|y1)) + log(P(x2|y1)) + … log(P(xn|y1)) + log(P(yi))
计算概率的自然对数会产生更大(负)的数,将这些数相加意味着更大的概率会更接近于零。结果值仍然可以进行比较和最大化,以得出最可能的类别标签。
在乘以概率时,这通常被称为对数技巧(log-trick)。
4. 更新概率分布
当有新数据可用时,将这些新数据与旧数据结合起来,更新每个变量概率分布的参数估计是相对直接的。
这使得模型能够轻松利用新数据或随时间变化的数据分布。
5. 用作生成模型
概率分布将总结每个类别标签下每个输入变量值的条件概率。
这些概率分布除了在分类模型中使用之外,还具有更广泛的用途。
例如,可以对准备好的概率分布进行随机抽样,以创建新的、合理的(plausible)数据实例。所假设的条件独立性可能意味着,根据数据集中输入变量之间实际相互依赖的程度,生成的示例或多或少是合理的。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
教程
书籍
- 机器学习, 1997.
- 机器学习:概率视角, 2012.
- 模式识别与机器学习, 2006.
- 数据挖掘:实用机器学习工具与技术,第4版,2016年。
API
- sklearn.datasets.make_blobs API.
- scipy.stats.norm API.
- 朴素贝叶斯,scikit-learn 文档.
- sklearn.naive_bayes.GaussianNB API
文章
总结
在本教程中,您了解了用于分类预测建模的朴素贝叶斯算法。
具体来说,你学到了:
- 如何将分类预测建模构建为条件概率模型。
- 如何使用贝叶斯定理解决分类的条件概率模型。
- 如何实现简化的贝叶斯定理进行分类,即朴素贝叶斯算法。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。


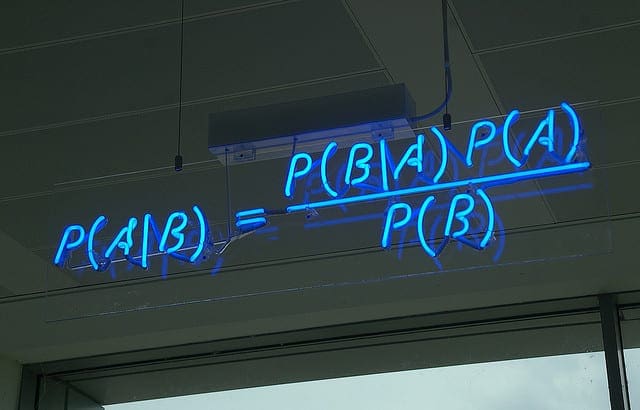




Jason博士,
我们都见过“鸢尾花数据”中三种不同鸢尾花(setosa、versicolor和virginica)的萼片长度与萼片宽度的散点图,一个例子可以在 https://bigqlabsdotcom.files.wordpress.com/2016/06/iris_data-scatter-plot-11.png?w=620 找到,来源是 https://bigqlabs.com/2016/06/27/training-a-naive-bayes-classifier-using-sklearn/。
我们在图中看到,在长度上存在一些重叠,即一些 versicolor 的长度与 virginica 的长度相同。
在存在重叠的情况下,是否有任何算法可以区分 virginica 和 versicolor?
换句话说,是否需要额外的变量来提高这三个物种之间预测的准确性?
这是因为到目前为止,仅依赖萼片长度和萼片宽度是不够的。
谢谢你,
悉尼的Anthony
也许你可以利用现有数据来构建新的输入特征?
尊敬的先生
我非常感谢您发给我的宝贵信息。这些对我的学习非常有帮助,我期待您能有更多这样的合作。
谢谢,我很高兴这些教程对您有帮助!
做得好,先生。请问,我该如何应用朴素贝叶斯规则来预测道路交通拥堵?例如,如果我正在监控大约3条不同路线(a、b和c)的交通。请回复我。
我建议遵循这个流程
https://machinelearning.org.cn/start-here/#process
概率对数的底数是多少?
我们使用对数概率相加来避免乘以许多小数,这可能导致下溢。
更简单的朴素贝叶斯实现如下
https://github.com/Bhavya112298/Machine-Learning-algorithms-scratch-implementation
感谢分享。
嘿,我有个问题,fit_prior 和 class_prior 是什么意思,我不懂,我读了文档还是不明白。先谢谢了
你具体不明白什么?
是的,我不明白这是什么意思,你能简单解释一下或者举个例子说明 fit_prior 和 class_prior 的用途吗?对不起,我的英语不好
类别先验概率是指在没有任何信息的情况下,任何一个观测值属于该类别的概率。
不知道你说的 fit prior 是什么意思,我以前没听说过。
谢谢您的回答,先生!
一篇写得很好的文章。嗯,我正在研究一个PGM查询模型,并且正在四处寻找关于如何最好地表示CPD(条件概率分布)的想法。它应该是一个字典的字典,还是数据框等,或者是两者的结合,其中索引是“入边”的枚举,而可能的节点值是列。可能会四处看看,如果找不到合适的,就构建一个自定义对象。如果我真的不爽,我就用Java来做 ????
也许可以原型化几种方法?
非常感谢您,先生!
不客气!
感谢您的教程。我理解朴素贝叶斯的概念,但在尝试使用朴素贝叶斯分类器将用户对产品的评分数据集分类为两个标签[相似评分;不相似评分]时仍然遇到问题。
注意,我使用的是'AppleStore.csv'数据集。
请帮忙,我刚接触这个领域。
也许这里的方法之一会有帮助
https://scikit-learn.cn/stable/modules/naive_bayes.html
这个可以用于4分类问题吗?
当然可以。
嗨,Jason,在类别分布为非高斯分布的情况下,我们能应用条件概率和贝叶斯分类器吗?我们是否有任何成本函数可以衡量分类模型在非高斯类别分布下的不确定性?
你可以为特征使用其他分布,甚至是核分布或经验分布。
不确定使用条件分布的情况,抱歉。
可以将每个特征/分布看作一个模型,而朴素贝叶斯则是这些较小模型的集成。
嗨,Jason,
我有一个数据集,其中既有分类变量也有数值变量。我决定对分类变量(A, B, C)使用二项分布,对数值变量(D, E, F)使用高斯分布。
我不想从头开始构建朴素贝叶斯模型。在sklearn或Python的任何其他库中,有没有办法告诉朴素贝叶斯模型,它必须将变量A、B、C视为二项分布,将变量D、E、F视为高斯分布?
谢谢回复
很好的问题。
凭直觉说,我认为 sklearn 的实现不支持混合类型。你可以为每种变量类型建立一个模型,然后将它们的预测结果集成起来。
嗨,Jason,
跟着您的思路,我读了一篇关于集成学习的文章。
下面是链接
https://www.datacamp.com/community/tutorials/ensemble-learning-python
这篇文章中写道,“此外,如果你需要在概率设置下工作,集成方法也可能不起作用。”
您可以自己核实一下。所以集成方法对朴素贝叶斯是行不通的。在Python中是否有处理混合类型的替代方案?
感谢您的回复。
我不同意这个说法,而且我没有读过那篇文章。概率方法在集成中一直被使用,并且是有效的。
你好,
好文章
但是我认为我看到了一个问题
当您使用 norm.pdf 函数时,您得到的是在提供的 x 值处的分布值 y——即似然。分布的高度并未归一化为1(其下的面积是1),这意味着您可能会得到各种与概率没有真正关系的数字,因为一个 pdf 值可能低于另一个,即使它更可能是第一个分布的样本。
当同一特征的两个分布(针对两个类别)具有相似的标准差时,这不会是一个大问题。但是,如果例如,一个分布的标准差是第二个的10倍,那么对于具有相同z分数的样本,它返回的pdf值将低10倍。
很乐意听听您的想法。
这就是pdf(概率密度函数)的本质。它是一个密度函数(可以是任何值),不应被解释为概率(介于0和1之间)。如果你想要一个类似概率的值,你可以考虑norm.cdf(累积分布函数),但你必须明白你在做什么。它并不总是可以直接替代的。
嗨,Jason,非常感谢您在文章中分享的宝贵信息。这些概念非常有帮助,仍然期待更多这样的内容。这些教程很有用。我欣赏朴素贝叶斯的概念。我也浏览了 https://www.edvanza.com/,也许这里的一些方法会有帮助。
感谢您的反馈和建议,Ernst!