如何配置梯度提升算法

梯度提升是应用机器学习中最强大的技术之一，因此也迅速成为最受欢迎的技术之一。

但是，如何针对您的问题配置梯度提升呢？

在这篇文章中，您将通过查阅书籍、论文以及竞赛中报告的配置，了解如何针对您的机器学习问题配置梯度提升。

阅读本文后，你将了解：

• 根据原始资料配置梯度提升的方法。
• 根据标准实现中的默认值和建议来配置算法的思路。
• 顶级Kaggle竞赛选手配置梯度提升和XGBoost的经验法则。

通过我的新书《XGBoost With Python》启动您的项目，其中包括所有示例的分步教程和 Python 源代码文件。

让我们开始吧。

如何配置梯度提升算法
图片由 Chris Sorge 拍摄，保留部分权利。

如何配置梯度提升机

在1999年的论文“贪婪函数逼近：梯度提升机”中，Jerome Friedman 评论了树的数量（M）和学习率（v）之间的权衡

v-M 权衡明显；v 值越小，最佳 M 值越大。它们还提供了更高的准确性，v < 0.125 时回报递减。对于 M > 200，误分类错误率非常平坦，因此其最佳 M 值不稳定。……这些结果的定性性质是相当普遍的。

他建议首先为树的数量设置一个较大的值，然后调整收缩参数以获得最佳结果。论文中的研究倾向于收缩值为0.1，树的数量在100到500之间，每棵树的终端节点数在2到8之间。

在1999年的论文“随机梯度提升”中，Friedman 重申了对收缩参数的偏好

“收缩”参数 0 < v < 1 控制过程的学习率。根据经验……，发现小值 (v <= 0.1) 会导致更好的泛化误差。

在论文中，Friedman 引入并实证研究了随机梯度提升（基于行的子采样）。他发现几乎所有子采样百分比都优于所谓的确定性提升，并且在某些问题上选择 30%-50% 是一个不错的值，在其他问题上选择 50%-80% 也是如此。

……最佳采样分数约为40% (f=0.4) ……然而，每次迭代仅采样30%甚至20%的数据比完全不采样有显著改进，并且计算速度分别加快了3倍和5倍。

他还研究了树中终端节点数量的影响，发现3和6这样的值比11、21和41这样的大值更好。

在这两种情况下，对100个目标平均的优化树大小为L = 6。通过使用更大的树来增加基础学习器的容量会因“过拟合”而降低性能。

在H2O题为“梯度提升机器学习”的演讲中，Trevor Hastie 评论说，一般来说，梯度提升优于随机森林，而随机森林又优于单个决策树。

梯度提升 > 随机森林 > 装袋 > 单个树

《统计学习要素：数据挖掘、推理和预测》一书的第10章“提升和加性树”专门讨论了提升。书中提供了配置梯度提升的启发式方法以及一些实证研究。

他们评论说，树中节点数 (J) 的一个好值大约是 6，通常在 4 到 8 之间。

尽管在许多应用中，J=2 将不足够，但不太可能需要 J>10。到目前为止的经验表明，4 <= J <= 8 在提升的背景下运行良好，结果对这个范围内的特定选择相当不敏感。

他们建议监控验证数据集上的性能，以校准树的数量，并在验证数据集上的性能开始下降时使用早期停止程序。

正如 Friedman 的第一篇梯度提升论文一样，他们评论了树的数量（M）和学习率（v）之间的权衡，并建议学习率取小于0.1的小值。

v值越小，在相同训练风险下M值越大，因此两者之间存在权衡。……实际上，最好的策略似乎是将v设置得非常小（v < 0.1），然后通过提前停止来选择M。

此外，正如 Friedman 的随机梯度提升论文所述，他们建议进行无放回抽样（n），采样比例约为 50%。

n 的典型值可以是 1/2，尽管对于大 N，n 可以远小于 1/2。

R中的梯度提升配置

梯度提升算法在 R 中以 gbm 包的形式实现。

回顾 软件包文档，gbm() 函数指定了合理的默认值

• n.trees = 100（树的数量）。
• interaction.depth = 1（叶子的数量）。
• n.minobsinnode = 10（树终端节点中的最小样本数）。
• shrinkage = 0.001（学习率）。

值得注意的是，这里使用了较小的收缩因子，并且默认情况下是使用树桩（stumps）。较小的收缩率由 Ridgeway 接下来解释。

在使用 R 中的 gbm 包的小插图“广义提升模型：gbm 包指南”中，Greg Ridgeway 提供了一些使用启发式方法。他建议首先将学习率（lambda）设置得尽可能小，然后使用交叉验证来调整树的数量（迭代次数或 T）。

在实践中，我将 lambda 设置得尽可能小，然后通过交叉验证选择 T。当 lambda 尽可能小时性能最佳，随着 lambda 越来越小，边际效用递减。

他解释了为什么将默认收缩率设置为0.001而不是0.1的理由。

重要的是要知道，较小的收缩值（几乎）总是能改善预测性能。也就是说，将 shrinkage=0.001 设置几乎肯定会比将 shrinkage=0.01 设置的模型产生更好的样本外预测性能。…… shrinkage=0.001 的模型可能需要是 shrinkage=0.01 模型的十倍迭代次数。

Ridgeway 还使用了相当多的树（此处称为迭代次数），是数千而不是数百。

我通常目标是 3,000 到 10,000 次迭代，收缩率在 0.01 到 0.001 之间。

scikit-learn 中的梯度提升配置

Python 库提供了梯度提升算法的实现，用于分类的类称为 GradientBoostingClassifier，用于回归的类称为 GradientBoostingRegressor。

回顾此库中算法的默认配置是有用的。

参数很多，但下面是一些关键的默认值。

• learning_rate=0.1（收缩率）。
• n_estimators=100（树的数量）。
• max_depth=3。
• min_samples_split=2。
• min_samples_leaf=1。
• subsample=1.0。

有趣的是，默认的收缩率与 Friedman 的研究相符，而且树的深度并未像 R 包那样设置为树桩。深度为 3 的树（如果生成的树是对称的）将有 8 个叶节点，与 Friedman 研究中首选的终端节点数量的上限相符（或者可以设置 max_leaf_nodes）。

在 scikit-learn 用户指南中，题为“梯度树提升”的部分中，作者评论说，设置最大叶节点的效果与将最大深度设置为最大叶节点减一类似，但会导致性能下降。

我们发现 max_leaf_nodes=k 给出了与 max_depth=k-1 可比的结果，但训练速度显著加快，代价是训练误差略高。

在一项演示梯度提升正则化方法的名为“梯度提升正则化”的小型研究中，结果显示了使用收缩和子采样的好处。

XGBoost中的梯度提升配置

XGBoost 库专门用于梯度提升算法。

它也指定了一些值得注意的默认参数，首先是 XGBoost 参数页面

• eta=0.3（收缩率或学习率）。
• max_depth=6。
• subsample=1。

这表明学习率和最大深度都高于我们在大多数研究和其他库中看到的。同样，我们可以总结 Python API 参考中 XGBoost 的默认参数。

• max_depth=3。
• learning_rate=0.1。
• n_estimators=100。
• subsample=1。

这些默认值通常与 scikit-learn 的默认值和论文中的建议更一致。

在 TechEd Europe 的一次题为“xgboost：一种用于快速准确梯度提升的 R 包”的演讲中，当被问及如何配置 XGBoost 时，Tong He 建议需要调整的三个最重要的参数是

• 树的数量。
• 树的深度。
• 步长（学习率）。

他还为新问题提供了一个简洁的配置策略。

1. 运行默认配置（并可能审查学习曲线？）。
2. 如果系统过拟合，则减慢学习速度（使用收缩？）。
3. 如果系统欠拟合，则加快学习速度以更激进（使用收缩？）。

在 Owen Zhang 2015 年在 NYC Data Science Academy 题为“赢得数据科学竞赛”的演讲中，他提供了一些使用 XGBoost 配置梯度提升的通用技巧。Owen 是梯度提升的重度用户。

我的坦白：我（过度）使用 GBM。犹豫不决时，就用 GBM。

他提供了一些配置梯度提升的技巧

• 学习率 + 树的数量：目标是 500 到 1000 棵树，并调整学习率。
• 叶子中的样本数：获得良好平均估计所需的观察数。
• 交互深度：10+。

在同一演讲的更新幻灯片中，他总结了常用的XGBoost参数

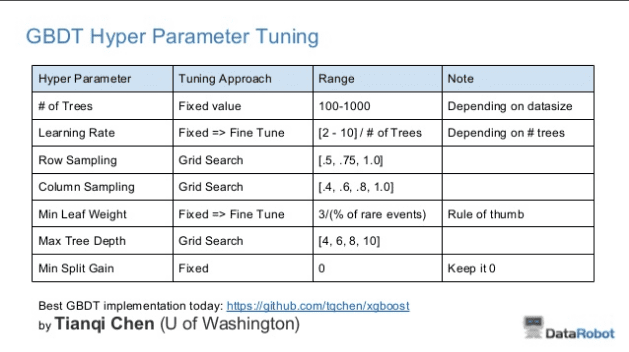
Owen Zhang 关于 XGBoost 超参数调整的建议表

我们可以在此表中看到一些有趣的事情。

• 简化了学习率和树的数量之间的关系，近似比例为：学习率 = [2-10]/树。
• 探讨了随机梯度提升的行和列抽样值。
• 探讨的最大深度范围与 Friedman 报告的范围大致相同（4-10）。
• 将最小叶权重调整为稀有事件数量百分比的约 3 倍。

在 Owen 在 ODSC Boston 2015 的一次类似演讲中，题为“开源工具和数据科学竞赛”，他再次总结了他常用的参数。

Owen Zhang 关于调整 XGBoost 的建议

我们可以看到一些可能相关的细微差异。

• 目标是 100 棵树而不是 1000 棵树，并调整学习率。
• 最小子权重为 1 除以事件率的平方根。
• 不进行行抽样。

最后，Abhishek Thakur 在其题为“解决（几乎）任何机器学习问题”的帖子中，提供了一个类似的表格，列出了关键的 XGBoost 参数和调整建议。

Abhishek Thakur 关于 XGBoost 调优的建议

这些分布确实涵盖了上述普遍的默认值以及更多。

有趣的是，Abhishek 确实提供了一些关于调整 alpha 和 beta 模型惩罚项以及行采样的建议。

总结

在这篇文章中，您深入了解了如何为自己的机器学习问题配置梯度提升。

具体来说，你学到了

• 关于树的数量和收缩之间的权衡以及子采样的良好默认值。
• 关于限制树大小和树深度及终端节点数量的良好默认值的不同想法。
• Kaggle 顶尖竞赛获胜者使用的网格搜索策略。

您对配置梯度提升或本文有任何疑问吗？请在评论中提出您的问题。

发现赢得竞赛的算法！

在几分钟内开发您自己的 XGBoost 模型

...只需几行 Python 代码

在我的新电子书中探索如何实现
使用 Python 实现 XGBoost

它涵盖了自学教程，例如：
算法基础、缩放、超参数等等……

将 XGBoost 的强大功能带入您自己的项目

跳过学术理论。只看结果。

查看内容