连续随机变量的概率可以用连续概率分布来概括。
在机器学习中会遇到连续概率分布,最常见的是模型中数值输入和输出变量的分布,以及模型所产生误差的分布。许多机器学习模型在执行密度和参数估计时,也需要了解正态连续概率分布。
因此,连续概率分布在应用机器学习中扮演着重要角色,从业者必须了解几种常见的分布。
在本教程中,您将了解机器学习中使用的连续概率分布。
完成本教程后,您将了解:
- 连续随机变量结果的概率可以使用连续概率分布进行概括。
- 如何对常见的连续概率分布进行参数化、定义和随机抽样。
- 如何为常见的连续概率分布创建概率密度和累积密度图。
通过我的新书《机器学习概率》来启动您的项目,其中包括分步教程和所有示例的 Python 源代码文件。
让我们开始吧。

机器学习中的连续概率分布
照片由 Bureau of Land Management 拍摄,保留部分权利。
教程概述
本教程分为四个部分;它们是
- 连续概率分布
- 正态分布
- 指数分布
- 帕累托分布
连续概率分布
随机变量是由随机过程产生的量。
连续随机变量是具有实数值的随机变量。
连续随机变量的每个数值结果都可以被赋予一个概率。
连续随机变量的事件与其概率之间的关系被称为连续概率分布,并由概率密度函数(简称 PDF)来概括。
与离散随机变量不同,给定连续随机变量的概率不能直接指定;相反,它是通过对特定结果周围一个微小区间进行积分(曲线下面积)来计算的。
等于或小于给定值的事件的概率由累积分布函数(简称 CDF)定义。CDF 的逆函数称为百分点函数,它将给出小于或等于某个概率的离散结果。
- PDF:概率密度函数,返回给定连续结果的概率。
- CDF:累积分布函数,返回小于或等于给定结果的值的概率。
- PPF:百分点函数,返回一个小于或等于给定概率的离散值。
有许多常见的连续概率分布。最常见的是正态概率分布。实际上,所有我们感兴趣的连续概率分布都属于所谓的指数分布族,这只是一组参数化的概率分布(例如,根据参数值而变化的分布)。
连续概率分布在机器学习中扮演着重要角色,从输入变量到模型的分布、模型产生误差的分布,以及在模型本身估计输入与输出之间映射关系时都有应用。
在接下来的章节中,我们将更仔细地研究一些更常见的连续概率分布。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
正态分布
正态分布也称为高斯分布(以卡尔·弗里德里希·高斯命名)或钟形曲线分布。
该分布涵盖了许多不同问题领域中实值事件的概率,使其成为一种常见且众所周知的分布,因此得名“正态”。具有正态分布的连续随机变量被称为“正态”或“正态分布”。
一些具有正态分布事件的领域示例如下:
- 人的身高。
- 婴儿的体重。
- 考试的分数。
该分布可以使用两个参数来定义:
- 均值 (mu):期望值。
- 方差 (sigma^2):与均值的离散程度。
通常,使用标准差代替方差,标准差计算为方差的平方根,即归一化。
- 标准差 (sigma):与均值的平均离散程度。
均值为零、标准差为 1 的分布称为标准正态分布,为了便于解释和比较,数据通常会缩减或“标准化”到此分布。
我们可以定义一个均值为 50、标准差为 5 的分布,并从此分布中抽样随机数。我们可以使用 NumPy 的 normal() 函数来实现这一点。
下面的示例从此分布中抽样并打印 10 个数字。
|
1 2 3 4 5 6 7 8 9 |
# 抽样一个正态分布 from numpy.random import normal # 定义分布 mu = 50 sigma = 5 n = 10 # 生成样本 sample = normal(mu, sigma, n) print(sample) |
运行该示例会打印出从定义的正态分布中随机抽样的 10 个数字。
|
1 2 |
[48.71009029 49.36970461 45.58247748 51.96846616 46.05793544 40.3903483 48.39189421 50.08693721 46.85896352 44.83757824] |
可以通过绘制数据样本并检查其是否具有熟悉的正态形状,或使用统计检验来判断其是否随机。如果随机变量的观测样本呈正态分布,那么它们可以仅用均值和方差来概括,这些参数可以直接从样本中计算得出。
我们可以使用概率密度函数计算每个观测值的概率。将这些值绘制成图,我们会得到标志性的钟形曲线。
我们可以使用 SciPy 的 norm() 函数定义一个正态分布,然后计算其属性,如矩、PDF、CDF 等。
下面的示例计算了我们分布中 30 到 70 之间整数值的概率并绘制了结果,然后对累积概率也做了同样的操作。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 正态分布的 pdf 和 cdf from scipy.stats import norm from matplotlib import pyplot # 定义分布参数 mu = 50 sigma = 5 # 创建分布 dist = norm(mu, sigma) # 绘制 pdf values = [value for value in range(30, 70)] probabilities = [dist.pdf(value) for value in values] pyplot.plot(values, probabilities) pyplot.show() # 绘制 cdf cprobs = [dist.cdf(value) for value in values] pyplot.plot(values, cprobs) pyplot.show() |
运行该示例首先计算范围 [30, 70] 内整数的概率,并创建一个值与概率的线图。
该图显示了高斯或钟形曲线,概率峰值出现在期望值或均值 50 附近,概率约为 8%。
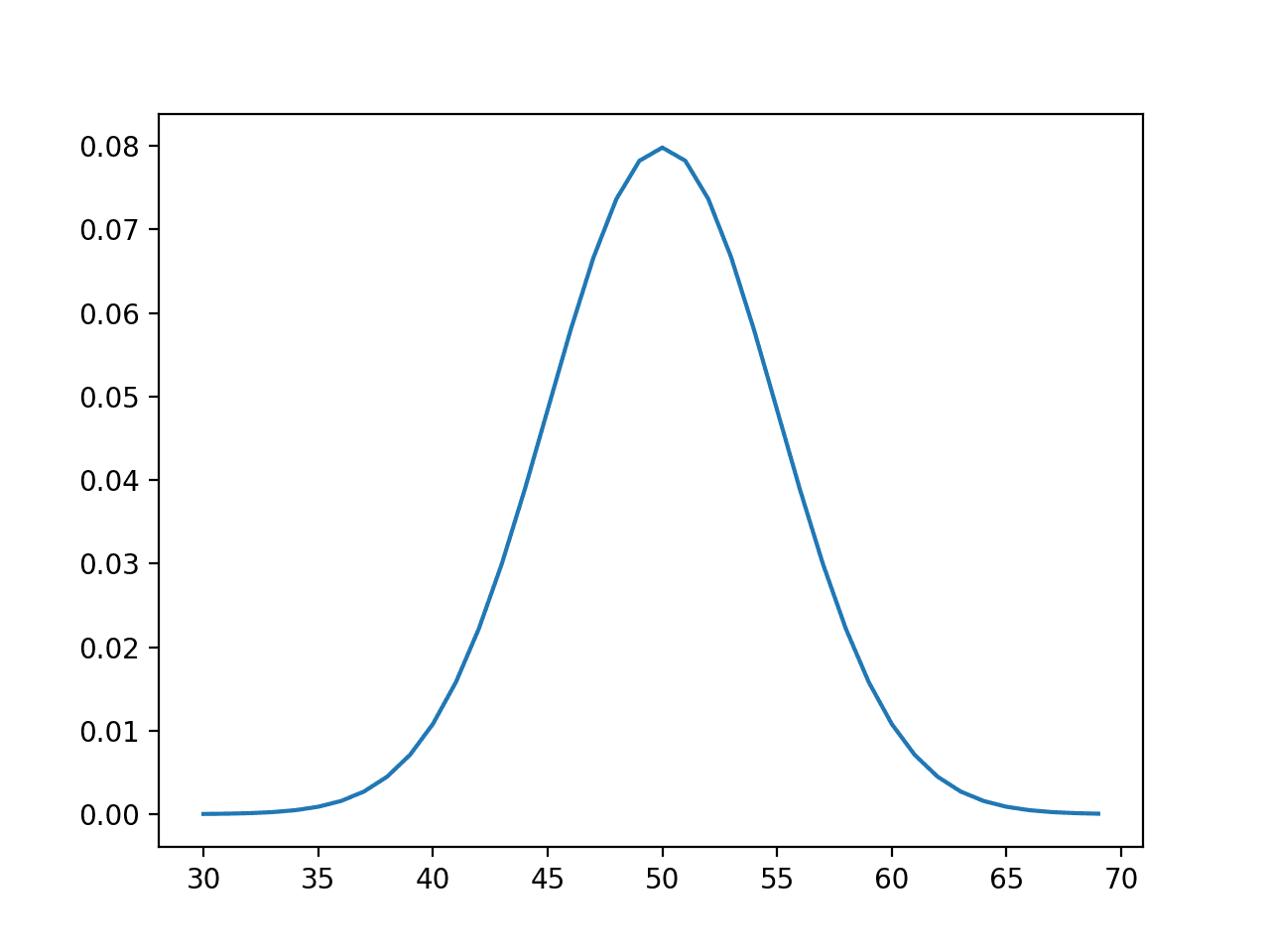
正态分布的事件与概率关系图或概率密度函数图
然后计算相同范围内观测值的累积概率,结果显示在均值处,我们已经覆盖了约 50% 的期望值,而在值约为 65(即距离均值 3 个标准差,50 + (3 * 5))之后,覆盖率接近 100%。
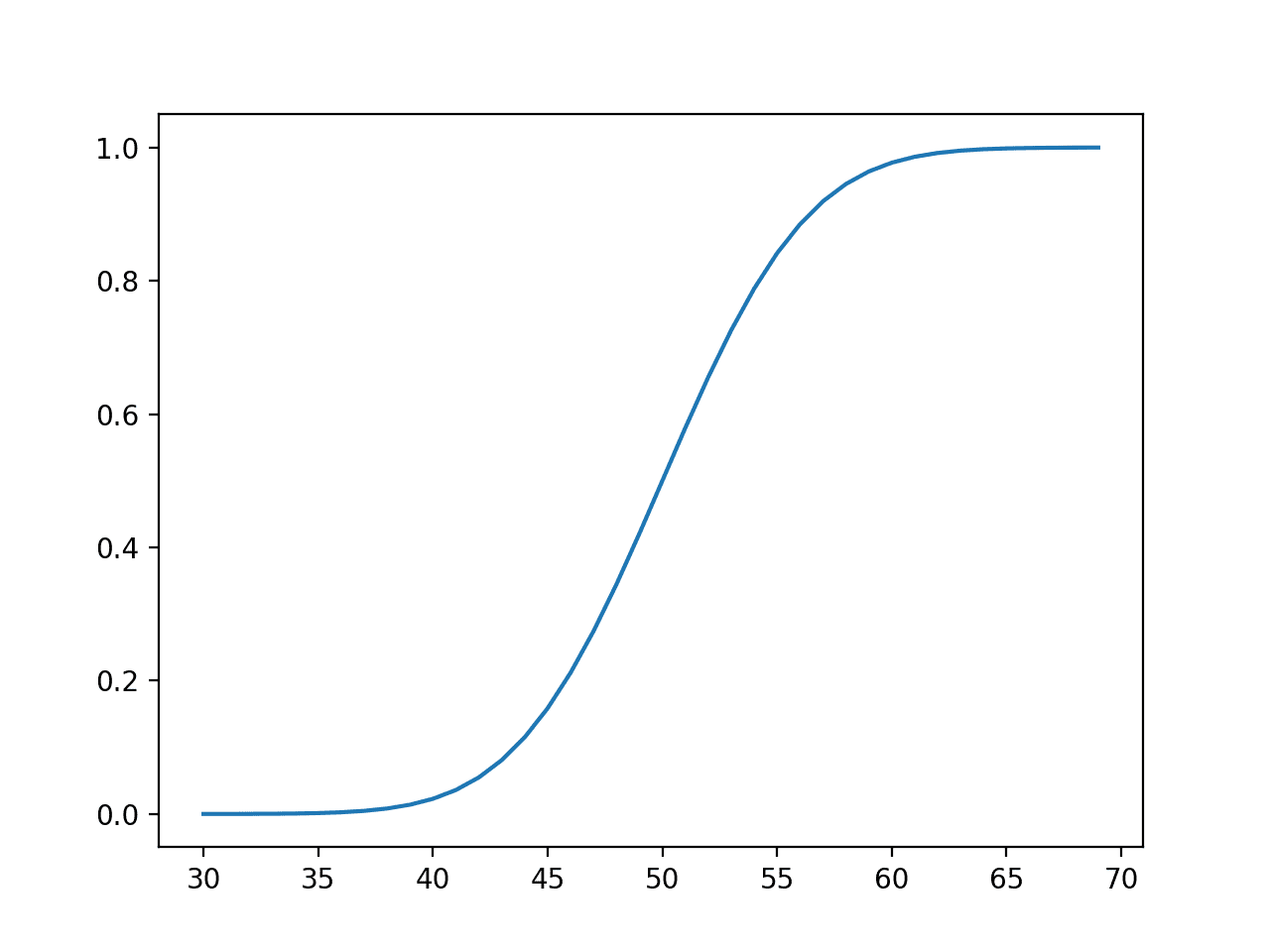
正态分布的事件与累积概率关系图或累积密度函数图
事实上,正态分布有一个启发式规则或经验法则,它通过距离均值的标准差数量来定义给定范围内数据所占的百分比。这被称为68-95-99.7法则,它分别是由距离均值 1、2 和 3 个标准差定义的范围所覆盖数据的近似百分比。
例如,在我们的均值为 50、标准差为 5 的分布中,我们预计 95% 的数据会落在距离均值 2 个标准差的范围内,即 50 – (2 * 5) 和 50 + (2 * 5) 之间,也就是 40 到 60 之间。
我们可以通过使用百分点函数计算确切值来证实这一点。
中间 95% 的范围将由百分点函数在低端 2.5% 和高端 97.5% 处的值来定义,其中 97.5% - 2.5% 得到中间的 95%。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 |
# 计算定义中间 95% 的值 from scipy.stats import norm # 定义分布参数 mu = 50 sigma = 5 # 创建分布 dist = norm(mu, sigma) low_end = dist.ppf(0.025) high_end = dist.ppf(0.975) print('中间 95%% 介于 %.1f 和 %.1f 之间' % (low_end, high_end)) |
运行该示例给出了定义中间 95% 预期结果的确切值,这与我们基于标准差的启发式值 40 和 60 非常接近。
|
1 |
中间 95% 介于 40.2 和 59.8 之间 |
一个重要的相关分布是对数正态概率分布。
指数分布
指数分布是一种连续概率分布,其中少数结果最有可能出现,而所有其他结果的概率则迅速下降。
它是离散随机变量中几何概率分布在连续随机变量中的对应形式。
一些具有指数分布事件的领域示例如下:
- 盖革计数器两次点击之间的时间。
- 一个部件失效前的时间。
- 一笔贷款违约前的时间。
该分布可以用一个参数来定义:
- 尺度 (Beta):分布的均值和标准差。
有时,该分布会用参数 lambda 或速率来更正式地定义。beta 参数定义为 lambda 参数的倒数(beta = 1/lambda)。
- 速率 (lambda) = 分布的变化率。
我们可以定义一个均值为 50 的分布,并从此分布中抽样随机数。我们可以使用 NumPy 的 exponential() 函数来实现这一点。
下面的示例从此分布中抽样并打印 10 个数字。
|
1 2 3 4 5 6 7 8 |
# 抽样一个指数分布 from numpy.random import exponential # 定义分布 beta = 50 n = 10 # 生成样本 sample = exponential(beta, n) print(sample) |
运行该示例会打印出从定义的分布中随机抽样的 10 个数字。
|
1 2 |
[ 3.32742946 39.10165624 41.86856606 85.0030387 28.18425491 68.20434637 106.34826579 19.63637359 17.13805423 15.91135881] |
我们可以使用 SciPy 的 expon() 函数定义一个指数分布,然后计算其属性,如矩、PDF、CDF 等。
下面的示例定义了一个 50 到 70 之间的观测范围,并计算了每个观测值的概率和累积概率,然后绘制了结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 指数分布的 pdf 和 cdf from scipy.stats import expon from matplotlib import pyplot # 定义分布参数 beta = 50 # 创建分布 dist = expon(beta) # 绘制 pdf values = [value for value in range(50, 70)] probabilities = [dist.pdf(value) for value in values] pyplot.plot(values, probabilities) pyplot.show() # 绘制 cdf cprobs = [dist.cdf(value) for value in values] pyplot.plot(values, cprobs) pyplot.show() |
运行该示例首先创建了一个结果与概率的线图,显示出熟悉的指数概率分布形状。
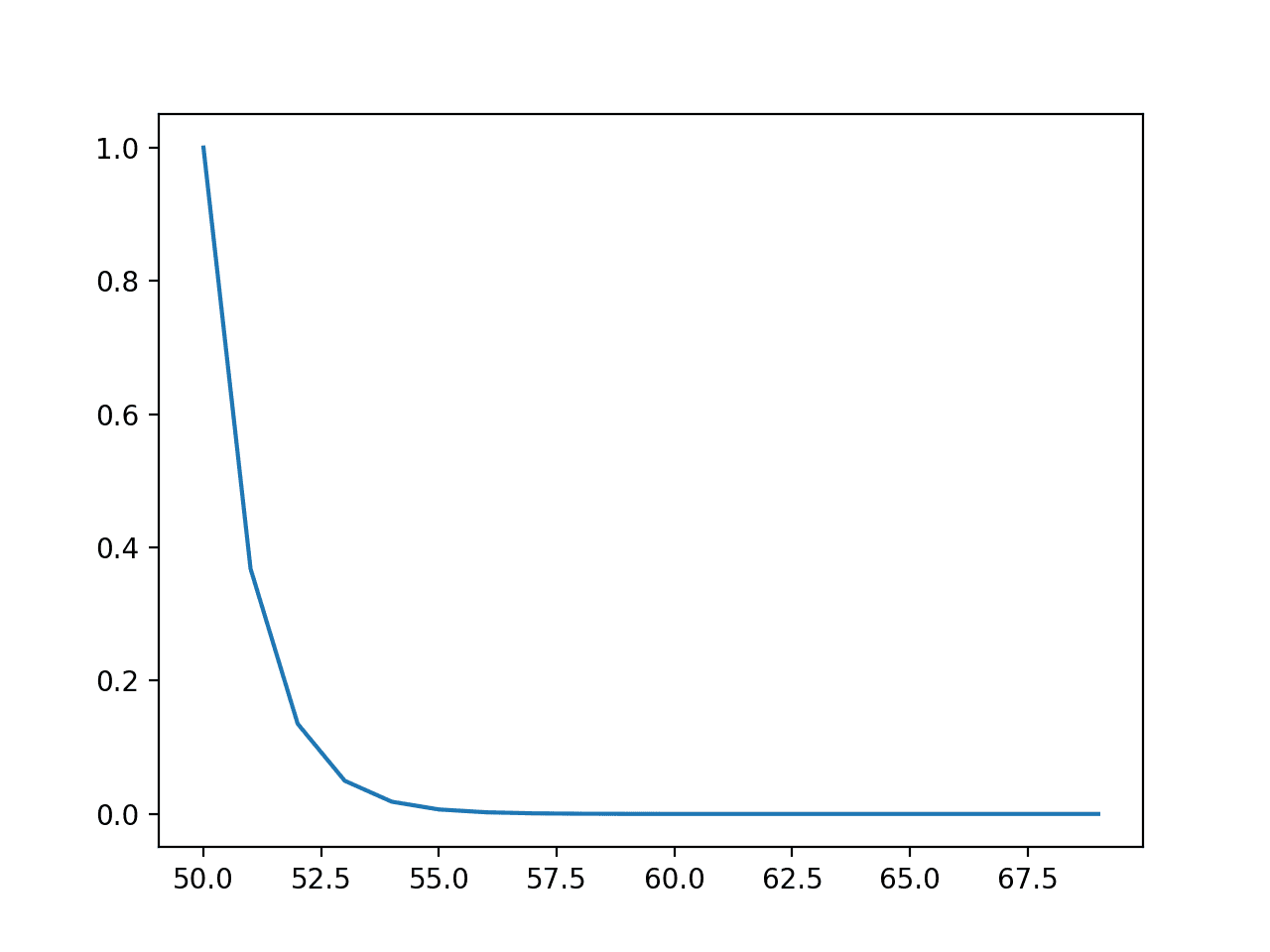
指数分布的事件与概率关系图或概率密度函数图
接下来,计算并绘制了每个结果的累积概率的线图,显示出在值大约为 55 之后,几乎 100% 的期望值都会被观测到。
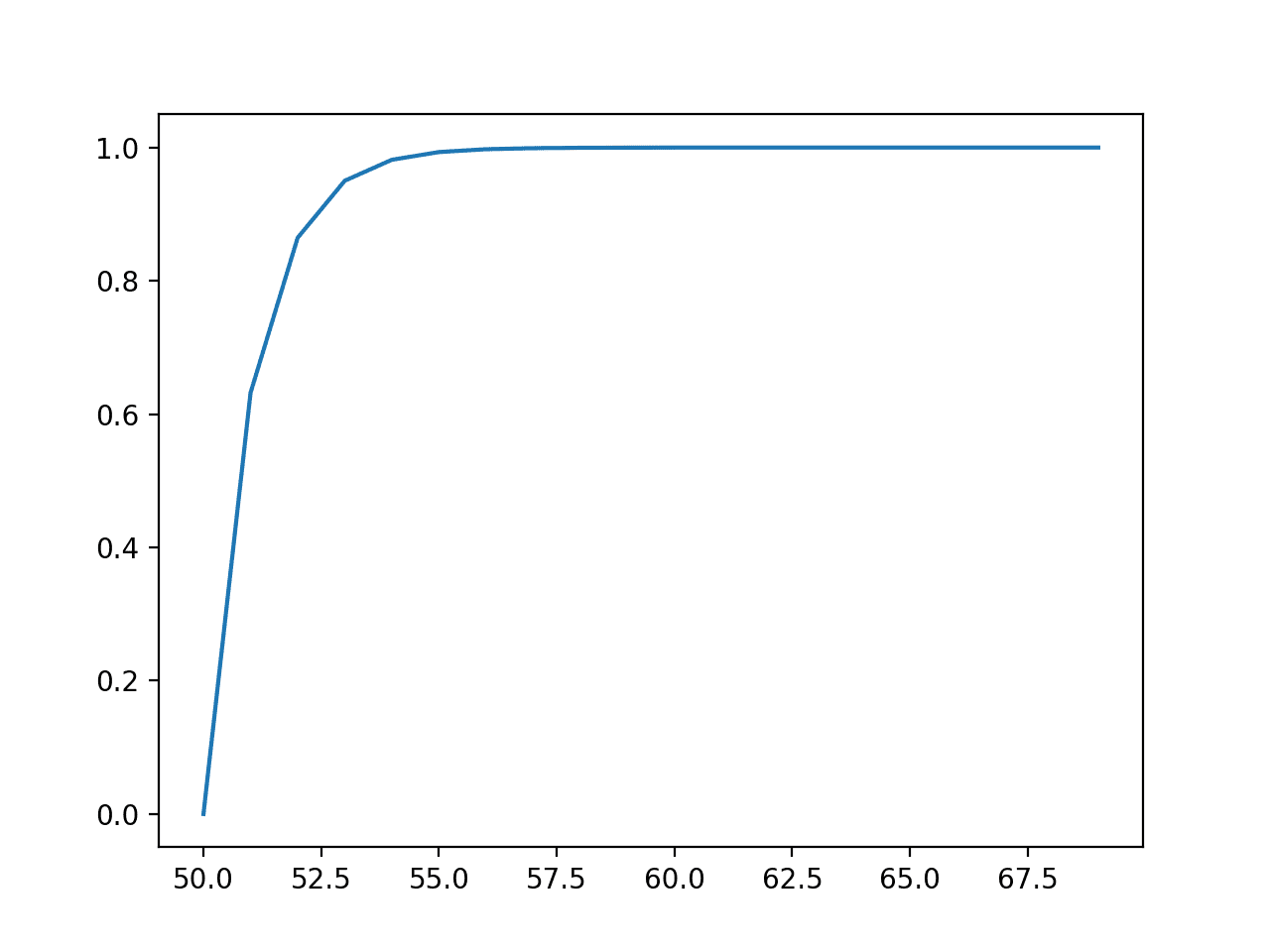
指数分布的事件与累积概率关系图或累积密度函数图
一个重要的相关分布是双指数分布,也称为拉普拉斯分布。
帕累托分布
它也与帕累托原则(或 80/20 法则)有关,该法则是针对遵循帕累托分布的连续随机变量的一种启发式规则,即 80% 的事件由 20% 的结果范围覆盖,例如,大多数事件都来自连续变量范围的仅 20%。
帕累托原则只是特定帕累托分布的一种启发式规则,特别是帕累托 II 型分布,这可能是最有趣的,我们也将重点关注它。
一些具有帕累托分布事件的领域示例如下:
- 一个国家家庭的收入。
- 书籍的总销售额。
- 运动队队员的得分。
该分布可以用一个参数来定义:
- 形状 (alpha):概率下降的陡峭程度。
形状参数的值通常很小,例如在 1 到 3 之间,当 alpha 设置为 1.161 时,即为帕累托原则。
我们可以定义一个形状参数为 1.1 的分布,并从此分布中抽样随机数。我们可以使用 NumPy 的 pareto() 函数来实现这一点。
|
1 2 3 4 5 6 7 8 |
# 抽样一个帕累托分布 from numpy.random import pareto # 定义分布 alpha = 1.1 n = 10 # 生成样本 sample = pareto(alpha, n) print(sample) |
运行该示例会打印出从定义的分布中随机抽样的 10 个数字。
|
1 2 |
[0.5049704 0.0140647 2.13105224 3.10991217 2.87575892 1.06602639 0.22776379 0.37405415 0.96618778 3.94789299] |
我们可以使用 SciPy 的 pareto() 函数定义一个帕累托分布,然后计算其属性,如矩、PDF、CDF 等。
下面的示例定义了一个从 1 到约 10 的观测范围,并计算了每个值的概率和累积概率,然后绘制了结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 帕累托分布的 pdf 和 cdf from scipy.stats import pareto from matplotlib import pyplot # 定义分布参数 alpha = 1.5 # 创建分布 dist = pareto(alpha) # 绘制 pdf values = [value/10.0 for value in range(10, 100)] probabilities = [dist.pdf(value) for value in values] pyplot.plot(values, probabilities) pyplot.show() # 绘制 cdf cprobs = [dist.cdf(value) for value in values] pyplot.plot(values, cprobs) pyplot.show() |
运行该示例首先创建了一个结果与概率的线图,显示出熟悉的帕累托概率分布形状。
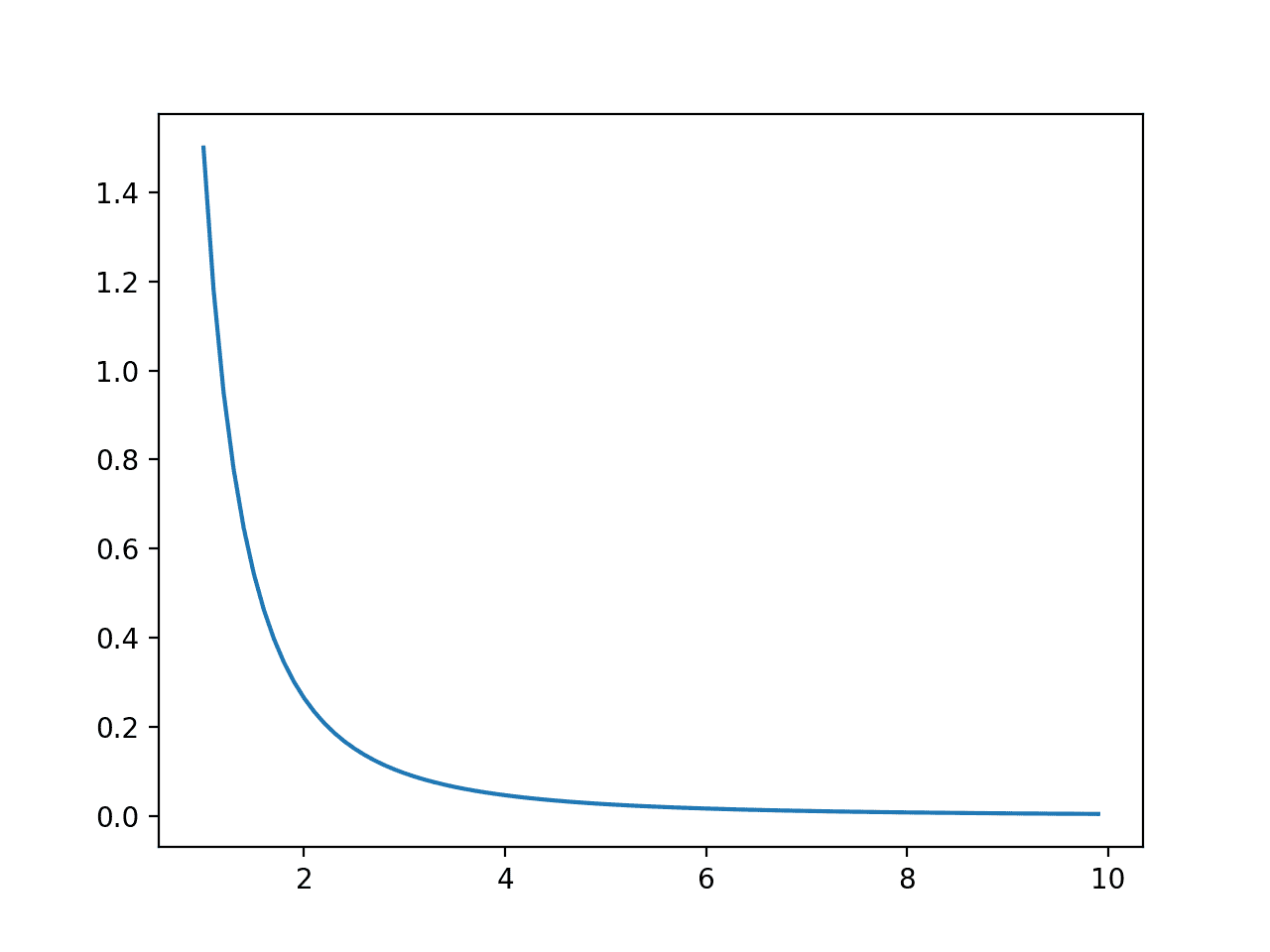
帕累托分布的事件与概率关系图或概率密度函数图
接下来,计算并绘制了每个结果的累积概率的线图,显示其上升趋势比上一节中看到的指数分布要平缓。
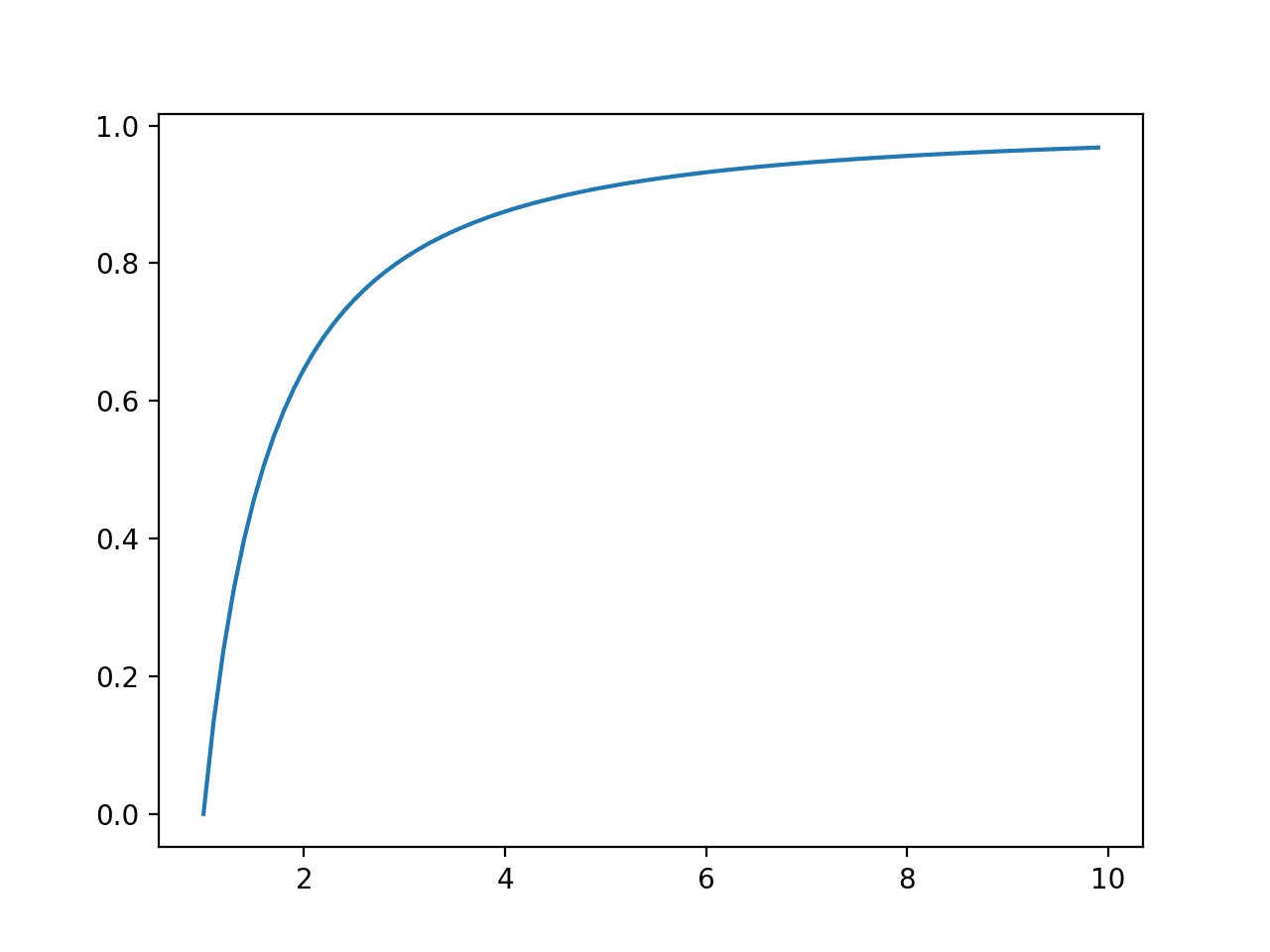
帕累托分布的事件与累积概率关系图或累积密度函数图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
API
文章
总结
在本教程中,您了解了机器学习中使用的连续概率分布。
具体来说,你学到了:
- 连续随机变量结果的概率可以使用连续概率分布进行概括。
- 如何对常见的连续概率分布进行参数化、定义和随机抽样。
- 如何为常见的连续概率分布创建概率密度和累积密度图。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





为什么了解数据的分布很重要?
假设我有 A B C D 四列
A 服从泊松分布
B 服从超几何分布
C 服从贝塔分布
D 服从威布尔分布
然后呢?这在机器学习或数据分析中如何帮助我?我应该做出什么样的决策?
Jason 先生,您能帮帮我吗?
我无法判断您举的例子中数据分布会是什么样的,但如果情况如此,对数据进行转换(例如,将数据映射回其累积分布函数 CDF)可以帮助您的模型。
我能知道如何做这个吗?
谢谢!
你好,我只是对分布的峰度感到好奇。当所有迹象都表明我们正在处理一个正态分布,但仅仅是峰度呈现尖峰或平峰状态时——这是否成为我们不应该对数据进行标准化的理由?我猜这不是什么大问题,但我至今没有找到任何关于这方面的评论。感谢您的帮助!
你好 Waheed……以下内容可能有助于澄清关于峰度的问题
https://www.analyticsvidhya.com/blog/2021/05/shape-of-data-skewness-and-kurtosis/
嗨,Jason 和团队,
关于连续分布的百分点函数(PPF),我有一个疑问。
此页面上说
“百分点函数,返回一个小于或等于给定概率的离散值。”
在这种情况下,它返回的是一个离散值吗?
我只是核对一下,因为这与关于离散分布指南中的表述相同。