R 中的凸优化

作者 Jason Brownlee 于 2019年8月22日发布在 R机器学习 7

优化是机器学习的重要组成部分。它是大多数流行方法的核心，从最小二乘回归到人工神经网络。

在这篇文章中，您将发现 R 中 5 种优化算法的配方。

这些方法可能对您自己实现机器学习算法的核心有用。您可能需要实现自己的算法调优方案，以优化模型参数以实现某个成本函数。

一个很好的例子是当您想优化来自多个子模型集合的预测混合体的超参数时。

使用我的新书《R 语言机器学习精通》，其中包含分步教程和所有示例的R 源代码文件，来启动您的项目。

让我们开始吧。

黄金分割法

黄金分割法是一种用于一维全局优化的线搜索方法。它是一种直接搜索（模式搜索）方法，因为它对函数进行采样以逼近导数，而不是直接计算导数。

黄金分割法与离散有序列表的模式搜索相关，例如二分搜索和斐波那契搜索。它与其他线搜索算法相关，例如 Brent 方法，以及更广泛地与其他直接搜索优化方法相关，例如 Nelder-Mead 方法。

该方法的信息处理目标是定位函数的极值。它通过直接对函数进行采样来实现，使用三个点组成的模式。这些点构成搜索的括号：第一个和最后一个点是当前搜索的边界，第三个点划分了中间空间。选择划分点是为了使较大部分与整个区间的比率与较大部分与较小部分的比率相同，即黄金分割比例（phi）。根据函数评估比较这些部分，并选择表现更好的部分作为新的搜索边界。该过程会递归进行，直到达到所需的精度（对最优值的括号）或搜索停滞。

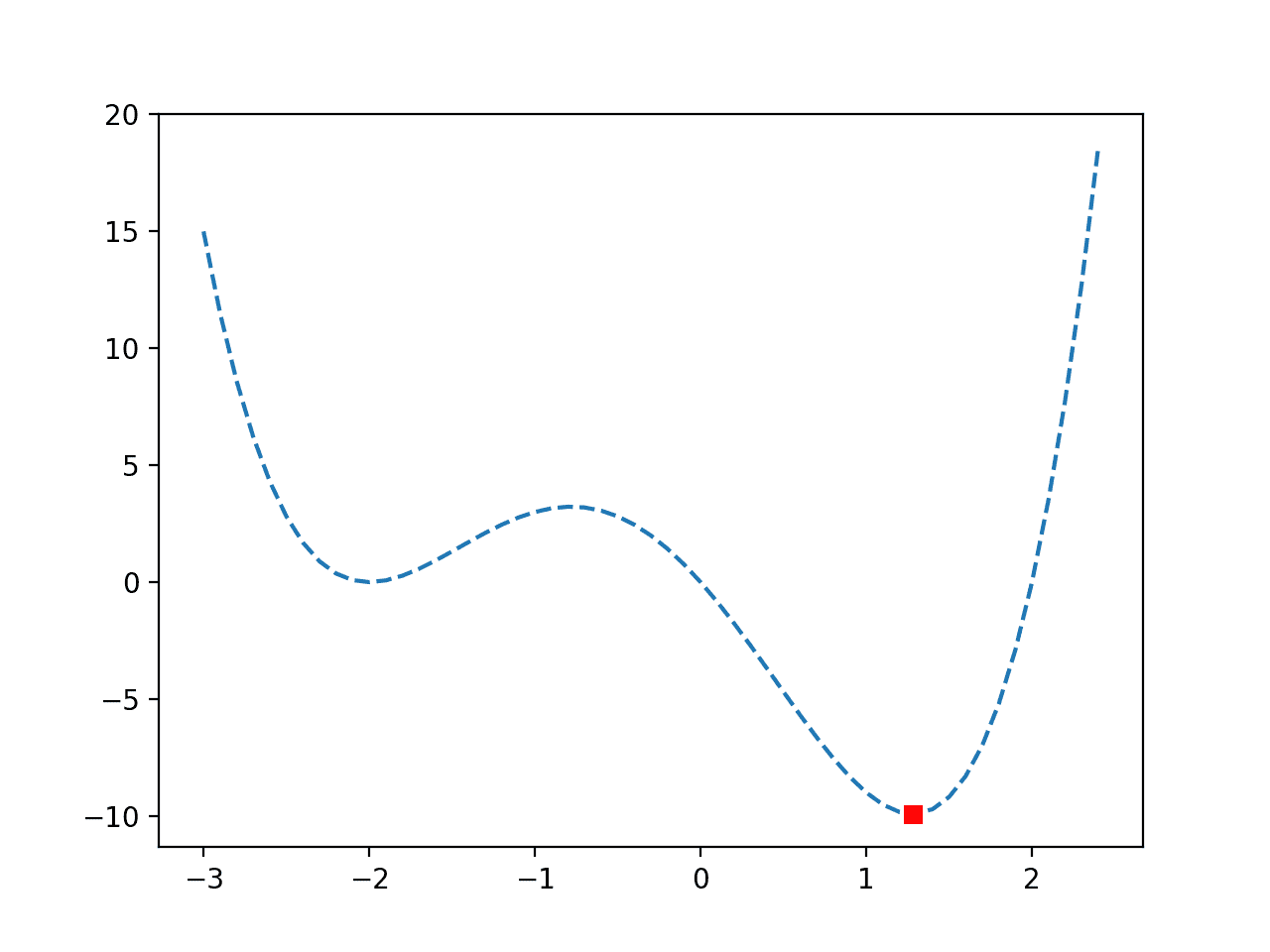
以下示例提供了 R 语言中黄金分割法方法的一个代码列表，用于解决一维非线性无约束优化函数。

# define a 1D basin function, optima at f(0)=0
basin <- function(x) {
x[1]^2
}

# locate the minimum of the function using a Golden Section Line Search
result <- optimize( 
basin, # the function to be minimized
c(-5, 5), # the bounds on the function parameter
maximum=FALSE, # we are concerned with the function minima
tol=1e-8) # the size of the final bracketing

# display the results
print(result$minimum)
print(result$objective)

# plot the function 
x <- seq(-5, 5, length.out=100)
y <- basin(expand.grid(x))
plot(x, y, xlab="x",ylab="f(x)", type="l")
# plot the solution as a point
points(result$minimum, result$objective, col="red", pch=19)
# draw a square around the optima to highlight it
rect(result$minimum-0.3, result$objective-0.7, result$minimum+0.3, result$objective+0.7, lwd=2)

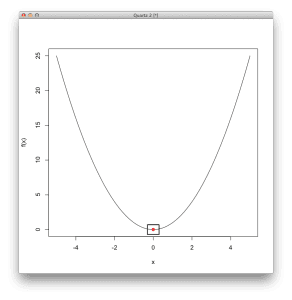
# 定义一个一维盆地函数，最优值为 f(0)=0

basin <- function(x) {

x[1]^2

}

# 使用黄金分割法线搜索定位函数的最小值

result <- optimize(

basin, # 要最小化的函数

c(-5, 5), # 函数参数的边界

maximum=FALSE, # 我们关心的是函数的最小值

tol=1e-8) # 最终括号的大小

# 显示结果

print(result$minimum)

print(result$objective)

# 绘制函数

x <- seq(-5, 5, length.out=100)

y <- basin(expand.grid(x))

plot(x, y, xlab="x",ylab="f(x)", type="l")

# 将解显示为点

points(result$minimum, result$objective, col="red", pch=19)

# 在最优值周围绘制一个正方形以突出显示

rect(result$minimum-0.3, result$objective-0.7, result$minimum+0.3, result$objective+0.7, lwd=2)

黄金分割法结果

用法提示

假设函数是凸的和单峰的，特别是函数只有一个最优值，并且它位于括号点之间。
旨在查找一维连续函数的极值。
它比等分区线搜索更有效。
终止条件是对最优值括号之间的最小距离的规定。
它可以快速定位最优值的括号区域，但在定位具体最优值方面效率较低。
一旦找到具有所需精度的解，它就可以作为具有更快收敛速度的第二搜索算法的基础。

需要更多关于R机器学习的帮助吗？

参加我为期14天的免费电子邮件课程，了解如何在您的项目中使用R（附带示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

Nelder Mead

Nelder-Mead 方法是一种用于多维非线性无约束函数优化的优化算法。
它是一种直接搜索方法，因为它在过程中不使用函数梯度。它是一种模式搜索，因为它使用几何模式来探索问题空间。

它与其他直接搜索优化方法相关，例如 Hooke 和 Jeeves 的模式搜索，后者也使用几何模式来优化目标函数。

Nelder-Mead 方法的信息处理目标是定位函数的极值。这是通过在域中覆盖一个单纯形（几何模式）来实现的，并迭代地增加和/或减小其大小，直到找到最优值。单纯形始终由 n+1 个顶点定义，其中 n 是搜索空间的维度（即，二维问题为三角形）。

该过程包括识别单纯形中表现最差的点，并用通过剩余点质心（中心点）反射的点替换它。单纯形可以通过远离最差点的扩展、远离最差点的沿一个维度的收缩或向最佳点收缩所有维度来变形（适应搜索空间的拓扑）。

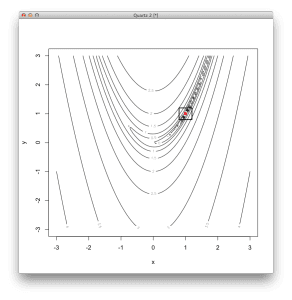
以下示例提供了一个 R 语言中 Nelder-Mead 方法的代码列表，用于解决二维非线性优化函数。

# definition of the 2D Rosenbrock function, optima is at (1,1)
rosenbrock <- function(v) { 
(1 - v[1])^2 + 100 * (v[2] - v[1]*v[1])^2
}

# locate the minimum of the function using the Nelder-Mead method
result <- optim(
c(runif(1,-3,3), runif(1,-3,3)), # start at a random position
rosenbrock, # the function to minimize
NULL, # no function gradient 
method="Nelder-Mead", # use the Nelder-Mead method
control=c( # configure Nelder-Mead
maxit=100, # maximum iterations of 100
reltol=1e-8, # response tolerance over-one step
alpha=1.0, # reflection factor
beta=0.5, # contraction factor
gamma=2.0)) # expansion factor

# summarize results
# the coordinate of the minimum
print(result$par) 
# the function response of the minimum
print(result$value) 
# the number of function calls performed
print(result$counts)

# display the function as a contour plot
x <- seq(-3, 3, length.out=100)
y <- seq(-3, 3, length.out=100)
z <- rosenbrock(expand.grid(x, y))
contour(x, y, matrix(log10(z), length(x)), xlab="x",ylab="y")
# draw the optima as a point
points(result$par[1], result$par[2], col="red", pch=19)
# draw a square around the optima to highlight it
rect(result$par[1]-0.2, result$par[2]-0.2, result$par[1]+0.2, result$par[2]+0.2, lwd=2)

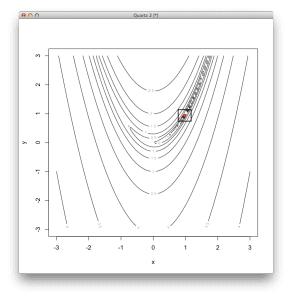
# 定义二维 Rosenbrock 函数，最优值为 (1,1)

rosenbrock <- function(v) {

(1 - v[1])^2 + 100 * (v[2] - v[1]*v[1])^2

}

# 使用 Nelder-Mead 方法定位函数的最小值

result <- optim(

c(runif(1,-3,3), runif(1,-3,3)), # 从随机位置开始

rosenbrock, # 要最小化的函数

NULL, # 没有函数梯度

method="Nelder-Mead", # 使用 Nelder-Mead 方法

control=c( # 配置 Nelder-Mead

maxit=100, # 最大迭代次数为 100

reltol=1e-8, # 一个步骤的响应容差

alpha=1.0, # 反射因子

beta=0.5, # 收缩因子

gamma=2.0) # 扩张因子

# 总结结果

# 最小值的坐标

print(result$par)

# 最小值处的函数响应

print(result$value)

# 执行的函数调用次数

print(result$counts)

# 以等高线图显示函数

x <- seq(-3, 3, length.out=100)

y <- seq(-3, 3, length.out=100)

z <- rosenbrock(expand.grid(x, y))

contour(x, y, matrix(log10(z), length(x)), xlab="x",ylab="y")

# 将最优值显示为点

points(result$par[1], result$par[2], col="red", pch=19)

# 在最优值周围绘制一个正方形以突出显示

rect(result$par[1]-0.2, result$par[2]-0.2, result$par[1]+0.2, result$par[2]+0.2, lwd=2)

Nelder Mead 结果

用法提示

它可以用于多维函数（一个或多个参数）和非线性响应面。
它不使用函数导数，这意味着它可以用于非可微函数、不连续函数、非光滑函数和噪声函数。
作为一种直接搜索方法，与现代基于导数的方法相比，它被认为效率低下且速度慢。
它依赖于起始位置，并且可能会陷入多峰函数中的局部最优值。
停止标准可以是最佳位置的最小变化。
单纯形结构的性质可能意味着它会卡在搜索空间中的非最优区域，如果初始单纯形的大小过大，这种情况更可能发生。
当该方法有效时（适用于要优化的函数），它已被证明快速且稳健。

梯度下降

梯度下降是一种用于无约束非线性函数优化的第一阶导数优化方法。之所以称为梯度下降，是因为它最初是为了函数最小化而设计的。当应用于函数最大化时，它可能被称为梯度上升。

最速下降搜索是一种扩展，它在线的梯度上执行线搜索以定位相邻的最优点（最优步长或最速步长）。批量梯度下降是一种扩展，其中成本函数及其导数是作为训练示例集合上的总误差计算的。随机梯度下降（或在线梯度下降）类似于批量梯度下降，只是成本函数和导数是为每个训练示例计算的。

该方法的信息处理目标是定位函数的极值。这是通过首先选择搜索空间中的一个起始点来实现的。对于搜索空间中的给定点，计算成本函数的导数，并在距离当前点 alpha（步长参数）的距离处沿函数导数的梯度向下选择一个新点。

该示例提供了一个 R 语言中梯度下降算法的代码列表，用于解决二维非线性优化函数。

# define a 2D basin function, optima is at (0,0)
basin <- function(x) {
x[1]^2 + x[2]^2
}

# define the derivative for a 2D basin function
derivative <- function(x) {
c(2*x[1], 2*x[2])
}

# definition of the gradient descent method in 2D
gradient_descent <- function(func, derv, start, step=0.05, tol=1e-8) {
pt1 <- start
grdnt <- derv(pt1)
pt2 <- c(pt1[1] - step*grdnt[1], pt1[2] - step*grdnt[2])
while (abs(func(pt1)-func(pt2)) > tol) {
pt1 <- pt2
grdnt <- derv(pt1)
pt2 <- c(pt1[1] - step*grdnt[1], pt1[2] - step*grdnt[2])
print(func(pt2)) # print progress
}
pt2 # return the last point
}

# locate the minimum of the function using the Gradient Descent method
result <- gradient_descent(
basin, # the function to optimize
derivative, # the gradient of the function
c(runif(1,-3,3), runif(1,-3,3)), # start point of the search 
0.05, # step size (alpha)
1e-8) # relative tolerance for one step

# display a summary of the results
print(result) # coordinate of fucntion minimum
print(basin(result)) # response of fucntion minimum

# display the function as a contour plot
x <- seq(-3, 3, length.out=100)
y <- seq(-3, 3, length.out=100)
z <- basin(expand.grid(x, y))
contour(x, y, matrix(z, length(x)), xlab="x",ylab="y")
# draw the optima as a point
points(result[1], result[2], col="red", pch=19)
# draw a square around the optima to highlight it
rect(result[1]-0.2, result[2]-0.2, result[1]+0.2, result[2]+0.2, lwd=2)

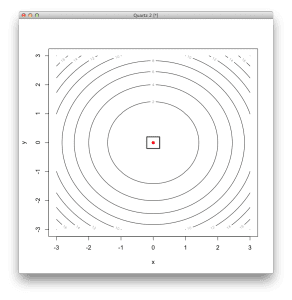
# 定义一个二维盆地函数，最优值为 (0,0)

basin <- function(x) {

x[1]^2 + x[2]^2

}

# 定义二维盆地函数的导数

derivative <- function(x) {

c(2*x[1], 2*x[2])

}

# 定义二维梯度下降方法

gradient_descent <- function(func, derv, start, step=0.05, tol=1e-8) {

pt1 <- start

grdnt <- derv(pt1)

pt2 <- c(pt1[1] - step*grdnt[1], pt1[2] - step*grdnt[2])

while (abs(func(pt1)-func(pt2)) > tol) {

pt1 <- pt2

grdnt <- derv(pt1)

pt2 <- c(pt1[1] - step*grdnt[1], pt1[2] - step*grdnt[2])

print(func(pt2)) # 打印进度

}

pt2 # 返回最后一个点

}

# 使用梯度下降方法定位函数的最小值

result <- gradient_descent(

basin, # 要优化的函数

derivative, # 函数的梯度

c(runif(1,-3,3), runif(1,-3,3)), # 搜索的起始点

0.05, # 步长 (alpha)

1e-8) # 一个步长的相对容差

# 显示结果摘要

print(result) # 函数最小值的坐标

print(basin(result)) # 函数最小值的响应

# 以等高线图显示函数

x <- seq(-3, 3, length.out=100)

y <- seq(-3, 3, length.out=100)

z <- basin(expand.grid(x, y))

contour(x, y, matrix(z, length(x)), xlab="x",ylab="y")

# 将最优值显示为点

points(result[1], result[2], col="red", pch=19)

# 在最优值周围绘制一个正方形以突出显示

rect(result[1]-0.2, result[2]-0.2, result[1]+0.2, result[2]+0.2, lwd=2)

梯度下降结果

用法提示

该方法仅限于查找局部最优值，如果函数是凸的，那么它也是全局最优值。
与现代方法相比，它被认为收敛效率低且速度慢（线性）。如果最优点处的梯度变平（梯度缓慢变为 0），收敛可能很慢。如果 Hessian 条件较差（梯度在某些方向上变化很快，而在另一些方向上变化较慢），收敛也可能很慢。
步长（alpha）可以恒定，可以随着搜索而调整，也可以整体或按维度维护。
该方法对初始条件敏感，因此，使用随机选择的初始位置重复搜索过程是常见的。
如果步长参数（alpha）太小，搜索通常需要大量迭代才能收敛；如果参数太大，可能会过冲函数的极值。
与非迭代函数优化方法相比，梯度下降在扩展到特征（维度）数量方面具有一些相对效率。

共轭梯度

共轭梯度法是一种用于多维非线性无约束函数的，基于一阶导数的优化方法。它与梯度下降法和最速下降法等其他一阶导数优化算法相关。

该技术的信息处理目标是定位函数的极值。从一个起始点开始，该方法首先计算梯度以确定最陡下降的方向，然后执行线搜索以确定最优步长（alpha）。之后，该方法会重复计算最陡方向、计算搜索方向以及执行线搜索以确定最优步长。一个参数beta根据梯度定义方向更新规则，可以通过多种方法计算。

共轭梯度法与最速下降法的区别在于，它使用共轭方向而不是局部梯度来向函数最小值移动，这可以非常高效。

该示例提供了在R语言中求解二维非线性优化函数的共轭梯度法的代码列表。

# definition of the 2D Rosenbrock function, optima is at (1,1)
rosenbrock <- function(v) { 
(1 - v[1])^2 + 100 * (v[2] - v[1]*v[1])^2
}

# definition of the gradient of the 2D Rosenbrock function
derivative <- function(v) {
c(-400 * v[1] * (v[2] - v[1]*v[1]) - 2 * (1 - v[1]), 
200 * (v[2] - v[1]*v[1]))
}

# locate the minimum of the function using the Conjugate Gradient method
result <- optim(
c(runif(1,-3,3), runif(1,-3,3)), # start at a random position
rosenbrock, # the function to minimize
derivative, # no function gradient 
method="CG", # use the Conjugate Gradient method
control=c( # configure Conjugate Gradient
maxit=100, # maximum iterations of 100
reltol=1e-8, # response tolerance over-one step
type=2)) # use the Polak-Ribiere update method

# summarize results
print(result$par) # the coordinate of the minimum
print(result$value) # the function response of the minimum
print(result$counts) # the number of function calls performed

# display the function as a contour plot
x <- seq(-3, 3, length.out=100)
y <- seq(-3, 3, length.out=100)
z <- rosenbrock(expand.grid(x, y))
contour(x, y, matrix(log10(z), length(x)), xlab="x", ylab="y")
# draw the optima as a point
points(result$par[1], result$par[2], col="red", pch=19)
# draw a square around the optima to highlight it
rect(result$par[1]-0.2, result$par[2]-0.2, result$par[1]+0.2, result$par[2]+0.2, lwd=2)

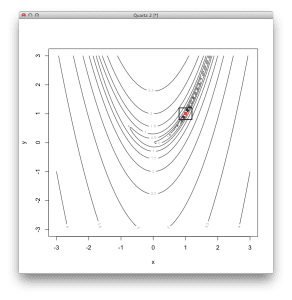
# 定义二维 Rosenbrock 函数，最优值为 (1,1)

rosenbrock <- function(v) {

(1 - v[1])^2 + 100 * (v[2] - v[1]*v[1])^2

}

# 2D Rosenbrock函数的梯度定义

derivative <- function(v) {

c(-400 * v[1] * (v[2] - v[1]*v[1]) - 2 * (1 - v[1]),

200 * (v[2] - v[1]*v[1]))

}

# 使用共轭梯度法定位函数的最小值

result <- optim(

c(runif(1,-3,3), runif(1,-3,3)), # 从随机位置开始

rosenbrock, # 要最小化的函数

derivative, # 无函数梯度

method="CG", # 使用共轭梯度法

control=c( # 配置共轭梯度法

maxit=100, # 最大迭代次数为 100

reltol=1e-8, # 一个步骤的响应容差

type=2)) # 使用Polak-Ribiere更新方法

# 总结结果

print(result$par) # 最小值的坐标

print(result$value) # 最小值的函数响应

print(result$counts) # 执行的函数调用次数

# 以等高线图显示函数

x <- seq(-3, 3, length.out=100)

y <- seq(-3, 3, length.out=100)

z <- rosenbrock(expand.grid(x, y))

contour(x, y, matrix(log10(z), length(x)), xlab="x", ylab="y")

# 将最优值显示为点

points(result$par[1], result$par[2], col="red", pch=19)

# 在最优值周围绘制一个正方形以突出显示

rect(result$par[1]-0.2, result$par[2]-0.2, result$par[1]+0.2, result$par[2]+0.2, lwd=2)

共轭梯度法结果

用法提示

它比最速下降法更有效，例如，它可以沿着狭窄山谷的直线路径下降，而最速下降法则必须之字形（弹球般）下降。
如果每迭代一次就重置共轭方向，则会退化为最速下降法。
它的速度几乎与二阶梯度方法一样快，对于合适的函数，只需要n次迭代就能找到最优值（其中n是参数的数量）。
它不维护Hessian矩阵（如BFGS），因此可能适用于具有许多变量的大型问题。
该方法在二次函数或类二次函数，或者在最优值附近函数近似为二次函数时最为有效。
在非凸问题上，该方法对其起始位置敏感。
学习率（步长alpha）不必指定，因为会使用线搜索来根据需要定位最优值。
计算方向更新规则（beta）的常用方法是Hestenes-Stiefel、Fletcher-Reeves、Polak-Ribiere和Beale-Sorenson方法。对于非二次函数，Polak-Ribiere方法在实践中通常效果更好。
它依赖于线搜索的精度，由此产生的误差以及响应曲面非二次的性质会导致方向更新更频繁，搜索效率降低。
为避免搜索退化，请考虑在迭代n次后重新启动搜索过程，其中n是函数参数的数量。

BFGS

BFGS是一种用于多维非线性无约束函数的优化方法。

BFGS属于拟牛顿（可变度量）优化方法系列，该方法利用了待优化函数的梯度（一阶导数）和Hessian矩阵（二阶导数）信息。更具体地说，它是一种拟牛顿方法，意味着它近似二阶导数而不是直接计算它。它与DFP方法、Broyden方法和SR1方法等其他拟牛顿方法相关。

BFGS的两个流行扩展是L-BFGS（Limited Memory BFGS），它的内存资源需求较低，以及L-BFGS-B（Limited Memory Boxed BFGS），它扩展了L-BFGS并对该方法施加了箱约束。

BFGS方法的信息处理目标是定位函数的极值。

这是通过迭代地构建一个良好的逆Hessian矩阵的近似来实现的。给定一个初始起始位置，它准备Hessian矩阵（二阶偏导数的方阵）的近似。然后，它重复使用近似的Hessian计算搜索方向、使用线搜索计算最优步长、更新位置，并更新Hessian近似的过程。每迭代一次更新Hessian的方法称为BFGS规则，该规则确保更新后的矩阵是正定的。

该示例提供了在R语言中求解二维非线性优化函数的BFGS方法的代码列表。

# definition of the 2D Rosenbrock function, optima is at (1,1)
rosenbrock <- function(v) { 
(1 - v[1])^2 + 100 * (v[2] - v[1]*v[1])^2
}

# definition of the gradient of the 2D Rosenbrock function
derivative <- function(v) {
c(-400 * v[1] * (v[2] - v[1]*v[1]) - 2 * (1 - v[1]), 200 * (v[2] - v[1]*v[1]))
}

# locate the minimum of the function using the BFGS method
result <- optim(
c(runif(1,-3,3), runif(1,-3,3)), # start at a random position
rosenbrock, # the function to minimize
derivative, # no function gradient 
method="BFGS", # use the BFGS method
control=c( # configure BFGS
maxit=100, # maximum iterations of 100
reltol=1e-8)) # response tolerance over-one step

# summarize results
print(result$par) # the coordinate of the minimum
print(result$value) # the function response of the minimum
print(result$counts) # the number of function calls performed

# display the function as a contour plot
x <- seq(-3, 3, length.out=100)
y <- seq(-3, 3, length.out=100)
z <- rosenbrock(expand.grid(x, y))
contour(x, y, matrix(log10(z), length(x)), xlab="x", ylab="y")
# draw the optima as a point
points(result$par[1], result$par[2], col="red", pch=19)
# draw a square around the optima to highlight it
rect(result$par[1]-0.2, result$par[2]-0.2, result$par[1]+0.2, result$par[2]+0.2, lwd=2)

# 定义二维 Rosenbrock 函数，最优值为 (1,1)

rosenbrock <- function(v) {

(1 - v[1])^2 + 100 * (v[2] - v[1]*v[1])^2

}

# 2D Rosenbrock函数的梯度定义

derivative <- function(v) {

c(-400 * v[1] * (v[2] - v[1]*v[1]) - 2 * (1 - v[1]), 200 * (v[2] - v[1]*v[1]))

}

# 使用BFGS方法定位函数的最小值

result <- optim(

c(runif(1,-3,3), runif(1,-3,3)), # 从随机位置开始

rosenbrock, # 要最小化的函数

derivative, # 无函数梯度

method="BFGS", # 使用BFGS方法

control=c( # 配置BFGS

maxit=100, # 最大迭代次数为 100

reltol=1e-8)) # 响应容差超过一步

# 总结结果

print(result$par) # 最小值的坐标

print(result$value) # 最小值的函数响应

print(result$counts) # 执行的函数调用次数

# 以等高线图显示函数

x <- seq(-3, 3, length.out=100)

y <- seq(-3, 3, length.out=100)

z <- rosenbrock(expand.grid(x, y))

contour(x, y, matrix(log10(z), length(x)), xlab="x", ylab="y")

# 将最优值显示为点

points(result$par[1], result$par[2], col="red", pch=19)

# 在最优值周围绘制一个正方形以突出显示

rect(result$par[1]-0.2, result$par[2]-0.2, result$par[1]+0.2, result$par[2]+0.2, lwd=2)

BFGS结果

使用启发式方法

它需要一个可以任意点计算函数梯度（一阶偏导数）的函数。
它不需要二阶导数，因为它近似Hessian矩阵，这使得它比牛顿法计算成本更低。
它需要相对较大的内存占用，因为它维护一个n*n的Hessian矩阵，其中n是变量的数量。这是该方法可扩展性的一个限制。
收敛速度是超线性，每次迭代的计算成本是O(n^2)。
BFGS的L-BFGS扩展适用于参数非常多的函数（>1000）。
停止条件通常是响应的最小变化或梯度的最小变化。
BFGS在搜索方向方面具有一定的鲁棒性和自我纠正能力，因此在确定步长时不需要使用精确的线搜索。

总结

优化是应用机器学习中理解和仔细应用的重要概念。

在这篇文章中，您发现了5种凸优化算法，以及可以在R语言中复制粘贴到您自己问题中的代码。

您还了解了每种方法的背景以及操作每种算法的一般启发式方法。

我是否遗漏了您最喜欢的凸优化算法？请留言告知。

关于此主题的更多信息

对R语言中的凸优化的7条回复

Joyce 2014年12月18日上午10:20 #

我目前正在R中进行这个与LASSO相关的项目。但是，由于研究的特定需要，我必须将惩罚函数更改为另一个平滑函数。问题是，我完全被R中所有成熟的包所宠坏，它们可以解决各种PLS问题。我已经使用“glmnet”来解决LASSO、ridge和elastic-net，使用“ncvreg”来解决SCAD。但我不知道应该使用哪个通用优化包来对我的目的的限制函数进行改进。您能否为我的困境提供一些启示？我将非常感谢您的帮助和建议。

回复
Dr. R. K. Verma 2015年6月22日上午10:45 #

亲爱的 Jason,

我是一名退休科学家，数学博士，专攻优化技术和IT领域。

您的文章《R语言中的凸优化》引起了我学习机器学习的兴趣。您能否通过发送我的机器学习文献和文献集来帮助我？这种合作可能会持续更长时间，并为数据分析和优化社区提供许多工具和技术！

祝您所有事业取得巨大成功，我
Dr. R. K. VERMA

回复
Dr. R. K. VERMA 2015年8月1日下午12:31 #

亲爱的 Jason,

我很欣赏您在R语言中的凸优化示例。

我的建议是：您发布一个关于“R语言中的优化方法”的系列，从线性规划到非线性规划。学术界和工业界的OR/MS社区将非常感谢这样的系列，相信我。

再次祝您取得巨大成功，我

Dr. R. K. Verma

回复
Connor 2017年11月17日上午6:06 #

您是否有用于约束不等式函数的梯度下降法代码？如果有，请分享。这将非常有帮助。

回复
- Jason Brownlee 2017年11月17日上午9:28 #
  
  我认为不行。
  
  回复
Mehrdad 2021年4月23日下午5:49 #

嗨，感谢您的文章，非常有用。
我在contour命令上遇到错误

Error in contour.default(x, y, matrix(log10(z), length(x)), xlab = “x”, : no proper ‘z’ matrix specified

请问是什么问题？
当我打印矩阵时，我得到的是
[,1]
[1,] Numeric,10000
[2,] Numeric,10000

重复100次。
请问是什么问题以及如何解决？谢谢！

回复
- Jason Brownlee 2021年4月24日上午5:18 #
  
  也许API自代码编写以来发生了变化？
  
  回复

导航

R 中的凸优化

黄金分割法

用法提示

需要更多关于R机器学习的帮助吗？

Nelder Mead

用法提示

梯度下降

用法提示

共轭梯度

用法提示

BFGS

使用启发式方法

总结

在R中发现更快的机器学习！

在几分钟内开发您自己的模型

最终将机器学习应用到您自己的项目中

关于此主题的更多信息

对R语言中的凸优化的7条回复

留下回复点击此处取消回复。

导航

黄金分割法

用法提示

需要更多关于R机器学习的帮助吗？

Nelder Mead

用法提示

梯度下降

用法提示

共轭梯度

用法提示

BFGS

使用启发式方法

总结

在R中发现更快的机器学习！

在几分钟内开发您自己的模型

最终将机器学习应用到您自己的项目中

关于此主题的更多信息

对R语言中的凸优化的7条回复

留下回复 点击此处取消回复。

留下回复点击此处取消回复。