分类变量至关重要,因为它们通常承载着影响预测模型结果的重要信息。然而,它们的非数值性质给模型处理带来了独特的挑战,需要特定的编码策略。本文将首先讨论数据集中常见的不同类型的分类数据。我们将深入探讨序数编码,以及如何在实现决策树回归器时利用它。通过使用 sklearn 中的 OrdinalEncoder 和 Ames 住房数据集的实际 Python 示例,本指南将为您提供有效实施这些策略的技能。此外,我们将直观地演示这些编码变量如何影响决策树回归器的决策。
通过我的书《进阶数据科学》启动您的项目。它提供了带有可运行代码的自学教程。
让我们开始吧。

决策树和序数编码
图片来源:Kai Pilger。保留部分权利。
概述
这篇博文分为三部分;它们是:
- 理解分类变量:序数与名义
- 在 Python 中实现序数编码
- 可视化决策树:序数编码数据的洞察
理解分类变量:序数与名义
数据集中的分类特征是基本要素,在预处理过程中需要仔细处理,以确保准确的模型预测。这些特征大致可分为两类:序数和名义。序数特征在其类别之间具有自然的顺序或层次结构。例如,Ames 数据集中的“ExterQual”特征描述了房屋外部材料的质量,其级别包括“差”、“一般”、“平均”、“好”和“优秀”。这些类别之间的顺序非常重要,可以在预测建模中加以利用。相比之下,名义特征不暗示任何固有的顺序。类别是独立的,并且它们之间没有顺序关系。例如,“Neighborhood”特征表示不同的社区名称,如“CollgCr”、“Veenker”、“Crawfor”等,没有任何内在的排名或层次结构。
分类变量的预处理至关重要,因为大多数机器学习算法需要数值格式的输入数据。这种从分类到数值的转换通常通过编码实现。编码策略的选择至关重要,并受分类变量类型和所用模型的影响。
机器学习模型的编码策略
线性模型,例如线性回归,通常对序数和名义特征都采用独热编码。这种方法将每个类别转换为一个新的二元变量,确保模型将每个类别视为一个独立的实体,没有任何序数关系。这至关重要,因为线性模型假定区间数据。也就是说,线性模型线性解释数值输入,这意味着分配给序数编码中每个类别的数值可能会误导模型。线性模型可能会错误地假定序数编码中每个增量整数值反映了基础定量度量的等步长增加,如果此假设不成立,则可能会扭曲模型输出。
基于树的模型,包括决策树和随机森林等算法,以不同的方式处理分类数据。这些模型可以从序数特征的序数编码中受益,因为它们根据特征值进行二元拆分。序数编码中保留的固有顺序可以帮助这些模型进行更有效的拆分。基于树的模型本质上不评估类别之间的算术差异。相反,它们评估在任何给定编码值处的特定拆分是否能最好地将目标变量分割为其类别或范围。与线性模型不同,这使得它们对类别间距的敏感度较低。
现在我们已经探讨了分类变量的类型及其对机器学习模型的影响,下一部分将指导您实际应用这些概念。我们将深入探讨如何使用 Ames 数据集在 Python 中实现序数编码,为您提供有效准备数据以进行模型训练的工具。
想开始学习进阶数据科学吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
在 Python 中实现序数编码
要在 Python 中实现序数编码,我们使用 sklearn.preprocessing 中的 OrdinalEncoder。此工具特别适用于为基于树的模型准备序数特征。它允许我们手动指定类别的顺序,确保编码尊重数据的自然层次结构。我们可以使用扩展数据字典中的信息来实现这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
# 导入必要的库 import pandas as pd from sklearn.pipeline import Pipeline from sklearn.impute import SimpleImputer from sklearn.compose import ColumnTransformer from sklearn.preprocessing import FunctionTransformer, OrdinalEncoder # 加载数据集 Ames = pd.read_csv('Ames.csv') # 根据数据字典手动指定序数编码的类别 ordinal_order = { 'Electrical': ['Mix', 'FuseP', 'FuseF', 'FuseA', 'SBrkr'], # 电气系统 'LotShape': ['IR3', 'IR2', 'IR1', 'Reg'], # 物业的一般形状 'Utilities': ['ELO', 'NoSeWa', 'NoSewr', 'AllPub'], # 可用的公用设施类型 'LandSlope': ['Sev', 'Mod', 'Gtl'], # 物业坡度 'ExterQual': ['Po', 'Fa', 'TA', 'Gd', 'Ex'], # 评估外部材料的质量 'ExterCond': ['Po', 'Fa', 'TA', 'Gd', 'Ex'], # 评估外部材料的当前状况 'BsmtQual': ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], # 地下室高度 'BsmtCond': ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], # 地下室的一般状况 'BsmtExposure': ['None', 'No', 'Mn', 'Av', 'Gd'], # 地下室墙壁的步出式或花园式 'BsmtFinType1': ['None', 'Unf', 'LwQ', 'Rec', 'BLQ', 'ALQ', 'GLQ'], # 地下室已完工区域的质量 'BsmtFinType2': ['None', 'Unf', 'LwQ', 'Rec', 'BLQ', 'ALQ', 'GLQ'], # 第二个地下室已完工区域的质量 'HeatingQC': ['Po', 'Fa', 'TA', 'Gd', 'Ex'], # 供暖质量和状况 'KitchenQual': ['Po', 'Fa', 'TA', 'Gd', 'Ex'], # 厨房质量 'Functional': ['Sal', 'Sev', 'Maj2', 'Maj1', 'Mod', 'Min2', 'Min1', 'Typ'], # 房屋功能 'FireplaceQu': ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], # 壁炉质量 'GarageFinish': ['None', 'Unf', 'RFn', 'Fin'], # 车库内部装修 'GarageQual': ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], # 车库质量 'GarageCond': ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], # 车库状况 'PavedDrive': ['N', 'P', 'Y'], # 铺砌车道 'PoolQC': ['None', 'Fa', 'TA', 'Gd', 'Ex'], # 泳池质量 'Fence': ['None', 'MnWw', 'GdWo', 'MnPrv', 'GdPrv'] # 围栏质量 } # 从字典中提取所有序数特征列表 ordinal_features = list(ordinal_order.keys()) # 除了 Electrical 之外的序数特征列表 ordinal_except_electrical = [feature for feature in ordinal_features if feature != 'Electrical'] # 用于“Electrical”的特定转换器,使用众数进行插补 electrical_imputer = Pipeline(steps=[ ('impute_electrical', SimpleImputer(strategy='most_frequent')) ]) # 填充其他序数特征的“None”的辅助函数 def fill_none(X): return X.fillna("None") # 序数特征的管道:将缺失值填充为“None” ordinal_imputer = Pipeline(steps=[ ('fill_none', FunctionTransformer(fill_none, validate=False)) ]) # 用于填充缺失值的预处理器 preprocessor_fill = ColumnTransformer(transformers=[ ('electrical', electrical_imputer, ['Electrical']), ('cat', ordinal_imputer, ordinal_except_electrical) ]) # 应用预处理器填充缺失值 Ames_ordinal = preprocessor_fill.fit_transform(Ames[ordinal_features]) # 转换回 DataFrame 以应用 OrdinalEncoder Ames_ordinal = pd.DataFrame(Ames_ordinal, columns=['Electrical'] + ordinal_except_electrical) # 应用序数编码 categories = [ordinal_order[feature] for feature in ordinal_features] ordinal_encoder = OrdinalEncoder(categories=categories) Ames_ordinal_encoded = ordinal_encoder.fit_transform(Ames_ordinal) Ames_ordinal_encoded = pd.DataFrame(Ames_ordinal_encoded, columns=['Electrical'] + ordinal_except_electrical) |
上面的代码块通过首先填充缺失值,然后应用适当的编码策略,有效地处理了分类变量的预处理。通过在编码之前查看数据集,我们可以确认我们的预处理步骤已正确应用
|
1 2 |
# 序数编码之前的 Ames 数据集(序数特征) print(Ames_ordinal) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Electrical LotShape Utilities LandSlope ... GarageCond PavedDrive PoolQC Fence 0 SBrkr Reg AllPub Gtl ... TA Y None None 1 SBrkr Reg AllPub Gtl ... TA Y None None 2 SBrkr Reg AllPub Gtl ... Po N None None 3 SBrkr Reg AllPub Gtl ... TA N None None 4 SBrkr Reg AllPub Gtl ... TA Y None None ... ... ... ... ... ... ... ... ... ... 2574 FuseF Reg AllPub Gtl ... Po P None None 2575 FuseA IR1 AllPub Gtl ... TA Y None None 2576 FuseA Reg AllPub Gtl ... TA Y None None 2577 SBrkr Reg AllPub Gtl ... TA Y None None 2578 SBrkr IR1 AllPub Gtl ... TA Y None None [2579 行 x 21 列] |
上面的输出强调了 Ames 数据集中在任何序数编码之前的序数特征。下面,我们说明提供给 OrdinalEncoder 的具体信息。请注意,我们不提供特征列表。我们只提供数据集中每个特征的排名顺序。
|
1 2 |
# 我们输入到序数编码器中的信息,它将自动分配 0, 1, 2, 3 等。 print(categories) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
[['Mix', 'FuseP', 'FuseF', 'FuseA', 'SBrkr'], ['IR3', 'IR2', 'IR1', 'Reg'], ['ELO', 'NoSeWa', 'NoSewr', 'AllPub'], ['Sev', 'Mod', 'Gtl'], ['Po', 'Fa', 'TA', 'Gd', 'Ex'], ['Po', 'Fa', 'TA', 'Gd', 'Ex'], ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], ['None', 'No', 'Mn', 'Av', 'Gd'], ['None', 'Unf', 'LwQ', 'Rec', 'BLQ', 'ALQ', 'GLQ'], ['None', 'Unf', 'LwQ', 'Rec', 'BLQ', 'ALQ', 'GLQ'], ['Po', 'Fa', 'TA', 'Gd', 'Ex'], ['Po', 'Fa', 'TA', 'Gd', 'Ex'], ['Sal', 'Sev', 'Maj2', 'Maj1', 'Mod', 'Min2', 'Min1', 'Typ'], ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], ['None', 'Unf', 'RFn', 'Fin'], ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], ['None', 'Po', 'Fa', 'TA', 'Gd', 'Ex'], ['N', 'P', 'Y'], ['None', 'Fa', 'TA', 'Gd', 'Ex'], ['None', 'MnWw', 'GdWo', 'MnPrv', 'GdPrv']] |
这为序数编码的有效应用奠定了基础,其中类别的自然顺序对于后续模型训练至关重要。特征中的每个类别都将转换为反映其指定等级或重要性的数值,而不假定它们之间存在等距间隔。
|
1 2 |
# 序数编码后的 Ames 数据集(序数特征) print(Ames_ordinal_encoded) |
转换后的数据集如下所示。强烈建议与原始数据集进行快速检查,以确保结果与我们从数据字典中获取的信息一致。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Electrical LotShape Utilities ... PavedDrive PoolQC Fence 0 4.0 3.0 3.0 ... 2.0 0.0 0.0 1 4.0 3.0 3.0 ... 2.0 0.0 0.0 2 4.0 3.0 3.0 ... 0.0 0.0 0.0 3 4.0 3.0 3.0 ... 0.0 0.0 0.0 4 4.0 3.0 3.0 ... 2.0 0.0 0.0 ... ... ... ... ... ... ... ... 2574 2.0 3.0 3.0 ... 1.0 0.0 0.0 2575 3.0 2.0 3.0 ... 2.0 0.0 0.0 2576 3.0 3.0 3.0 ... 2.0 0.0 0.0 2577 4.0 3.0 3.0 ... 2.0 0.0 0.0 2578 4.0 2.0 3.0 ... 2.0 0.0 0.0 [2579 行 x 21 列] |
在本节关于实现序数编码的结尾,我们为稳健的分析奠定了基础。通过将每个序数特征精确地映射到其固有的层次值,我们使预测模型能够更好地理解和利用数据中固有的结构化关系。对编码细节的仔细关注为更具洞察力和精确度的建模铺平了道路。
可视化决策树:序数编码数据的洞察
本文的最后一部分,我们将深入探讨决策树回归器如何解释和利用这些经过精心编码的数据。我们将通过视觉方式探索决策树的决策过程,突出我们特征的序数性质如何影响模型中的路径和决策。这种视觉描绘不仅将证实正确数据准备的重要性,还将以具体的方式阐明模型的推理。现在,分类变量已经过深思熟虑的预处理和编码,我们的数据集已为下一个关键步骤做好了准备:训练决策树回归器。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 基于上述代码块 # 导入必要的库 来自 sklearn.tree 导入 DecisionTreeRegressor from sklearn.model_selection import train_test_split import dtreeviz # 加载并分割数据 X_ordinal = Ames_ordinal_encoded # 仅使用序数特征拟合模型 y = Ames['SalePrice'] X_train, X_test, y_train, y_test = train_test_split(X_ordinal, y, test_size=0.2, random_state=42) # 初始化并拟合决策树 tree_model = DecisionTreeRegressor(max_depth=3) tree_model.fit(X_train.values, y_train) # 使用 dtreeviz 可视化决策树 viz = dtreeviz.model(tree_model, X_train, y_train, target_name='SalePrice', feature_names=X_train.columns.tolist()) # 在 Jupyter Notebook 中,可以直接使用以下代码查看可视化结果 # viz.view() # 渲染并显示 SVG 可视化 # 在 PyCharm 中,可以渲染并显示 SVG 图像 v = viz.view() # 将 SVG 渲染到内部对象 v.show() # 弹出窗口 |
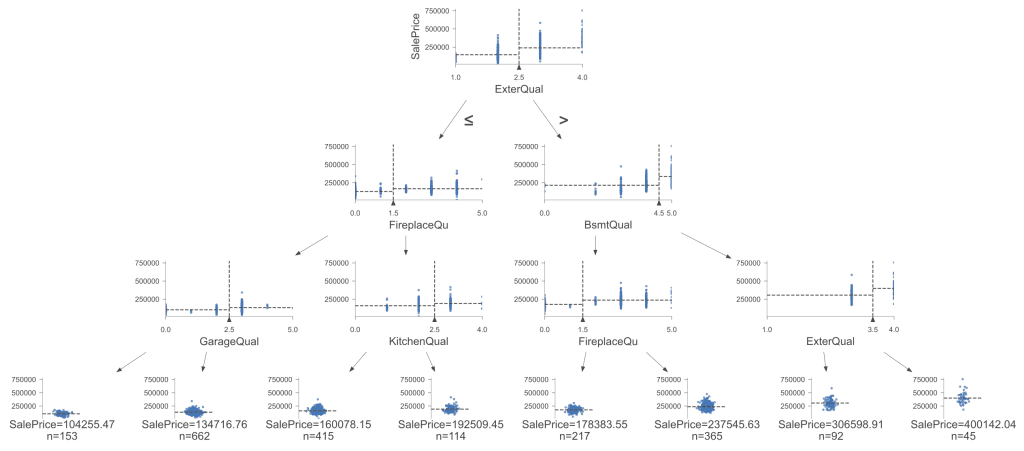
通过可视化决策树,我们提供了模型如何处理特征以得出预测的图形表示
这棵树中用于分割的特征包括“ExterQual”、“FireplaceQu”、“BsmtQual”、“GarageQual”和“KitchenQual”。选择这些特征是基于它们在分割数据时降低 MSE 的能力。这些分割的级别或阈值(例如,ExterQual <= 2.5)是在训练过程中确定的,以优化将数据点分离成更同质的组。这种可视化不仅证实了我们编码策略的有效性,还展示了决策树为预测建模带来的战略深度。
进一步阅读
API
教程
Ames 住房数据集和数据字典
总结
在本文中,您研究了序数和名义分类变量之间的区别。通过使用 Python 和 sklearn 中的 OrdinalEncoder 实现序数编码,您以尊重数据固有顺序的方式准备了 Ames 数据集。最后,您亲身体验了如何通过可视化决策树和编码数据来提供切实的洞察,从而更清晰地了解模型如何根据您提供的特征进行预测。
具体来说,你学到了:
- 分类变量的基本区别:理解序数变量和名义变量之间的区别。
- 模型特定的预处理需求:不同的模型,如线性回归器和决策树,需要对分类数据进行定制的预处理以优化其性能。
- 序数编码中的手动指定:在
OrdinalEncoder中使用“categories”来自定义您的编码策略。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。







暂无评论。