您将通过描述性统计学,在 Ames 数据集上开启您的数据科学之旅。Ames 住房数据集的丰富性使得描述性统计学能够将数据提炼成有意义的摘要。这是分析的初始步骤,提供数据集主要方面的简明摘要。它们的意义在于简化复杂性,帮助数据探索,促进比较分析,并实现数据驱动的叙述。
当您深入 Ames 物业数据集时,您将探索描述性统计学的变革力量,将大量数据提炼成有意义的摘要。在此过程中,您将发现关键指标及其解释的细微之处,例如平均值大于中位数在偏度方面的含义。
让我们开始吧。

解码数据:Ames 住房数据集的描述性统计学导论
图片来源:lilartsy。部分权利保留。
概述
这篇博文分为三部分;它们是:
- 描述性统计学基础
- Ames 数据集的数据探索
- 视觉叙事
描述性统计学基础
这篇文章将向您展示如何利用描述性统计学来理解数据。让我们回顾一下统计学如何帮助描述数据。
集中趋势:数据的核心
集中趋势捕捉数据集的核心或典型值。最常见的度量包括:
- 均值(平均值):所有值的总和除以值的数量。
- 中位数:数据排序后位于中间的值。
- 众数:出现频率最高的值。
离散度:分布与变异性
离散度揭示数据集内的分布和变异性。关键度量包括:
- 极差:最大值与最小值之间的差。
- 方差:与均值平方差的平均值。
- 标准差:方差的平方根。
- 四分位距 (IQR):第 25 百分位数与第 75 百分位数之间的范围。
形状与位置:数据的轮廓和地标
形状和位置揭示数据集的分布形式和关键标记,其特征如下:
- 偏度:分布的不对称性。如果中位数大于均值,则称数据为左偏(大值更常见)。反之,则为右偏。
- 峰度:分布的“尾部厚度”。换句话说,您看到异常值的频率。如果您看到极端大或极端小的值比正态分布更频繁,则称数据为尖峰态。
- 百分位数:低于该值的观测值百分比。第 25、50 和 75 百分位数也称为四分位数。
描述性统计学赋予数据声音,使其能够简洁明了地讲述自己的故事。
通过我的书《数据科学初学者指南》启动您的项目。它提供自学教程和工作代码。
Ames 数据集的数据探索
为了深入研究 Ames 数据集,我们将重点放在“SalePrice”属性上。
|
1 2 3 4 5 6 7 |
# 导入库并加载数据集 import pandas as pd Ames = pd.read_csv('Ames.csv') # 销售价格的描述性统计 sales_price_description = Ames['SalePrice'].describe() print(sales_price_description) |
|
1 2 3 4 5 6 7 8 9 |
计数 2579.000000 均值 178053.442420 标准差 75044.983207 最小值 12789.000000 25% 129950.000000 50% 159900.000000 75% 209750.000000 最大值 755000.000000 名称: SalePrice, 数据类型: float64 |
这总结了“SalePrice”,展示了计数、均值、标准差和百分位数。
|
1 2 3 4 5 |
median_saleprice = Ames['SalePrice'].median() print("中位数销售价格:", median_saleprice) mode_saleprice = Ames['SalePrice'].mode().values[0] print("众数销售价格:", mode_saleprice) |
|
1 2 |
中位数 销售 价格: 159900.0 众数 销售 价格: 135000 |
Ames 房屋的平均“SalePrice”(或均值)约为 178,053.44 美元,而中位数价格为 159,900 美元,这表明一半的房屋售价低于此值。这些度量之间的差异暗示高价值房屋影响了平均值,而众数则提供了对最频繁销售价格的洞察。
|
1 2 3 4 5 6 7 8 9 10 11 |
range_saleprice = Ames['SalePrice'].max() - Ames['SalePrice'].min() print("销售价格范围:", range_saleprice) variance_saleprice = Ames['SalePrice'].var() print("销售价格方差:", variance_saleprice) std_dev_saleprice = Ames['SalePrice'].std() print("销售价格标准差:", std_dev_saleprice) iqr_saleprice = Ames['SalePrice'].quantile(0.75) - Ames['SalePrice'].quantile(0.25) print("销售价格 IQR:", iqr_saleprice) |
|
1 2 3 4 |
销售 价格 范围: 742211 销售 价格 方差: 5631749504.563301 销售 价格 标准差: 75044.9832071625 销售 价格 IQR: 79800.0 |
“SalePrice”的范围从 12,789 美元到 755,000 美元,展示了 Ames 物业价值的巨大多样性。方差约为 56.3 亿美元,凸显了价格的巨大变异性,标准差约为 75,044.98 美元进一步强调了这一点。代表数据中间 50% 的四分位距 (IQR) 为 79,800 美元,反映了住房价格中心部分的分布。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
skewness_saleprice = Ames['SalePrice'].skew() print("销售价格偏度:", skewness_saleprice) kurtosis_saleprice = Ames['SalePrice'].kurt() print("销售价格峰度:", kurtosis_saleprice) tenth_percentile = Ames['SalePrice'].quantile(0.10) ninetieth_percentile = Ames['SalePrice'].quantile(0.90) print("第 10 百分位数:", tenth_percentile) print("第 90 百分位数:", ninetieth_percentile) q1_saleprice = Ames['SalePrice'].quantile(0.25) q2_saleprice = Ames['SalePrice'].quantile(0.50) q3_saleprice = Ames['SalePrice'].quantile(0.75) print("Q1(第 25 百分位数):", q1_saleprice) print("Q2(中位数/第 50 百分位数):", q2_saleprice) print("Q3(第 75 百分位数):", q3_saleprice) |
|
1 2 3 4 5 6 7 |
销售 价格 偏度: 1.7607507033716905 销售 价格 峰度: 5.430410648673599 第 10 百分位数: 107500.0 第 90 百分位数: 272100.0000000001 Q1 (第 25 百分位数): 129950.0 Q2 (中位数/第 50 百分位数): 159900.0 Q3 (第 75 百分位数): 209750.0 |
Ames 的“SalePrice”显示出约 1.76 的正偏度,表明分布的右侧有一个更长或更粗的尾部。这种偏度强调平均销售价格受到一部分高价房产的影响,而大多数房屋的交易价格低于此平均值。这种偏度量化了分布中的不对称性或偏离对称性的程度,突出了高价房产在提高平均值方面的不成比例的影响。当平均(均值)销售价格超过中位数时,它微妙地表明存在高价房产,导致右偏分布,其中尾部明显向右延伸。峰度值约为 5.43 进一步强调了这些见解,表明可能存在异常值或极端值,它们增加了分布的厚尾。
深入研究,四分位数提供了对数据集中趋势的洞察。Q1 位于 129,950 美元,Q3 位于 209,750 美元,这些四分位数涵盖了四分位距,代表了数据的中间 50%。这种划分强调了价格的中心分布,提供了对价格范围的细致描绘。此外,第 10 和第 90 百分位数分别位于 107,500 美元和 272,100 美元,充当了关键的分界线。这些百分位数划定了 80% 房屋价格所处的边界,突出了房地产估值的广阔范围,并强调了 Ames 住房市场的多面性。
视觉叙事
可视化使数据栩栩如生,讲述它的故事。让我们深入了解 Ames 数据集中“SalePrice”特征的视觉叙事。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
# 导入可视化库 import matplotlib.pyplot as plt import seaborn as sns # 设置样式 sns.set_style("whitegrid") # 计算 SalePrice 的均值、中位数、众数 mean_saleprice = Ames['SalePrice'].mean() median_saleprice = Ames['SalePrice'].median() mode_saleprice = Ames['SalePrice'].mode().values[0] # 绘制直方图 plt.figure(figsize=(14, 7)) sns.histplot(x=Ames['SalePrice'], bins=30, kde=True, color="skyblue") plt.axvline(mean_saleprice, color='r', linestyle='--', label=f"均值:${mean_saleprice:.2f}") plt.axvline(median_saleprice, color='g', linestyle='-', label=f"中位数:${median_saleprice:.2f}") plt.axvline(mode_saleprice, color='b', linestyle='-.', label=f"众数:${mode_saleprice:.2f}") # 计算 SalePrice 的偏度和峰度 skewness_saleprice = Ames['SalePrice'].skew() kurtosis_saleprice = Ames['SalePrice'].kurt() # 偏度和峰度的注释 plt.annotate('偏度:{:.2f}\n峰度:{:.2f}'.format(Ames['SalePrice'].skew(), Ames['SalePrice'].kurt()), xy=(500000, 100), fontsize=14, bbox=dict(boxstyle="round,pad=0.3", edgecolor="black", facecolor="aliceblue")) plt.title('Ames 住房价格直方图,包含 KDE 和参考线') plt.xlabel('住房价格') plt.ylabel('频率') plt.legend() plt.show() |
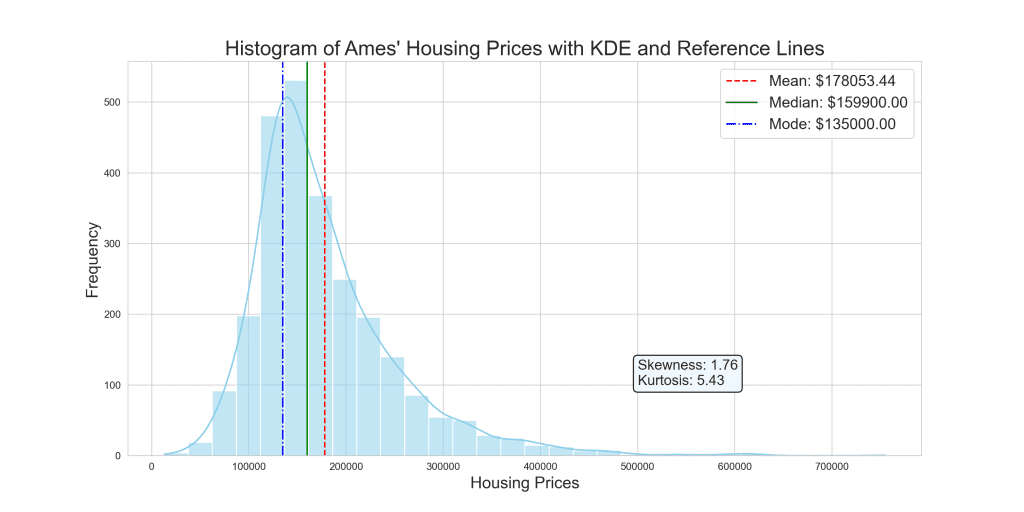
上面的直方图提供了 Ames 住房价格引人注目的视觉表示。在 150,000 美元附近明显的高峰突显了房屋在此特定价格区间内的显著集中。与直方图相辅相成的是核密度估计(KDE)曲线,它提供了数据分布的平滑表示。KDE 本质上是直方图的估计,但具有无限窄的 bin 的优势,提供了更连续的数据视图。它作为直方图的“限制”或精炼版本,捕捉了离散分箱方法中可能遗漏的细微之处。
值得注意的是,KDE 曲线的右偏尾部与我们之前计算的正偏度一致,强调了低于均值的房屋价格更密集。红色(均值)、绿色(中位数)和蓝色(众数)的彩色线作为关键标记,可以快速比较和理解分布的集中趋势与更广泛的数据格局。总而言之,这些视觉元素提供了对 Ames 住房价格分布和特征的全面洞察。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
from matplotlib.lines import Line2D # 带注释的水平箱线图 plt.figure(figsize=(12, 8)) # 绘制指定颜色和样式的箱线图 sns.boxplot(x=Ames['SalePrice'], color='skyblue', showmeans=True, meanprops={"marker": "D", "markerfacecolor": "red", "markeredgecolor": "red", "markersize":10}) # 绘制 Q1、中位数和 Q3 的箭头 plt.annotate('Q1', xy=(q1_saleprice, 0.30), xytext=(q1_saleprice - 70000, 0.45), arrowprops=dict(edgecolor='black', arrowstyle='->'), fontsize=14) plt.annotate('Q3', xy=(q3_saleprice, 0.30), xytext=(q3_saleprice + 20000, 0.45), arrowprops=dict(edgecolor='black', arrowstyle='->'), fontsize=14) plt.annotate('中位数', xy=(q2_saleprice, 0.20), xytext=(q2_saleprice - 90000, 0.05), arrowprops=dict(edgecolor='black', arrowstyle='->'), fontsize=14) # 标题、标签和图例 plt.title('Ames 住房价格箱线图', fontsize=16) plt.xlabel('住房价格', fontsize=14) plt.yticks([]) # 隐藏 y 轴刻度标签 plt.legend(handles=[Line2D([0], [0], marker='D', color='w', markerfacecolor='red', markersize=10, label='均值')], loc='upper left', fontsize=14) plt.tight_layout() plt.show() |
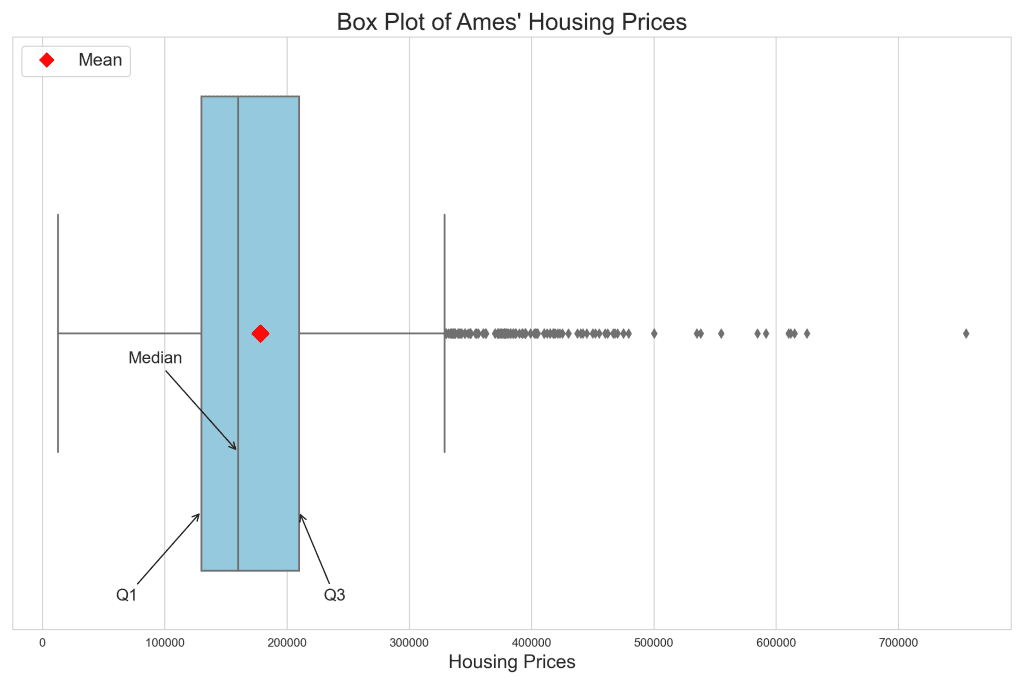
箱线图提供了集中趋势、范围和异常值的简洁表示,提供了 KDE 曲线或直方图无法轻易描绘的洞察。四分位距 (IQR) 从 Q1 延伸到 Q3,捕捉了数据的中间 50%,清晰地展示了价格的中心范围。此外,代表均值的红色菱形位于中位数的右侧,强调了高价值房产对平均值的影响。
箱线图解释的核心是其“触须”。左触须从箱体的左边缘延伸到下限内的最小数据点,表示价格在 Q1 以下 1.5 倍 IQR 范围内。相比之下,右触须从箱体的右边缘延伸到上限内的最大数据点,包含价格在 Q3 以上 1.5 倍 IQR 范围内的价格。这些触须作为边界,描绘了数据超出中间 50% 的分布,超出这些点的通常被标记为潜在异常值。
异常值,显示为单个点,突出显示价格特别高的房屋,可能是豪宅,或具有独特特征的房屋。箱线图中的异常值是低于 Q1 以下 1.5 倍 IQR 或高于 Q3 以上 1.5 倍 IQR 的点。在上面的图中,低端没有异常值,但高端有很多。识别和理解这些异常值至关重要,因为它们可以突出 Ames 住房市场中独特的市场动态或异常。
像这样的可视化将原始数据注入生命,编织引人入胜的叙事,并揭示可能隐藏在单纯数字中的见解。展望未来,认识和拥抱可视化在数据分析中的深远影响至关重要——它具有独特的传达仅凭文字或数字无法捕捉到的细微差别和复杂性的能力。
想开始学习数据科学新手指南吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
进一步阅读
如果您想深入了解此主题,本节提供了更多资源。
资源
总结
在本教程中,我们使用描述性统计学深入研究了 Ames 住房数据集,以揭示有关房地产销售的关键见解。我们计算并可视化了基本的统计量,强调了集中趋势、离散度和形状的价值。通过利用视觉叙事和数据分析,我们将原始数据转化为引人入胜的故事,揭示了 Ames 住房价格的复杂性和模式。
具体来说,你学到了:
- 如何利用描述性统计学从 Ames 住房数据集中提取有意义的见解,重点关注“SalePrice”属性。
- 均值、中位数、众数、极差和 IQR 等度量的重要性,以及它们如何讲述 Ames 住房价格的故事。
- 视觉叙事的力量,尤其是直方图和箱线图,在视觉上表示和解释数据的分布和变异性方面。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。






暂无评论。