统计学家和数据科学家面临的一个重大挑战是多重共线性,特别是其最严重的形式——完美多重共线性。这个问题在具有许多特征的大型数据集中常常难以察觉,可能会隐藏自身并扭曲统计模型的结果。
在本文中,我们将探讨检测、处理和完善受完美多重共线性影响的模型的方法。通过实际分析和示例,我们旨在为您提供提高模型鲁棒性和可解释性所需的工具,确保它们能够提供可靠的见解和准确的预测。
通过我的书《进阶数据科学》启动您的项目。它提供了带有可运行代码的自学教程。
让我们开始吧。

在大数据集中检测和克服完全多重共线性
图片作者:Ryan Stone。部分权利保留。
概述
这篇博文分为三部分;它们是:
- 探索完美多重共线性对线性回归模型的影响
- 使用 Lasso 回归处理多重共线性
- 利用 Lasso 回归的见解完善线性回归模型
探索完美多重共线性对线性回归模型的影响
多元线性回归因其可解释性而备受推崇。它可以直接了解每个预测变量如何影响响应变量。然而,其有效性取决于特征独立的假设。
共线性意味着一个变量可以表示为某些其他变量的线性组合。因此,变量之间不是相互独立的。
线性回归在特征集没有共线的假设下工作。为了确保此假设成立,理解线性代数中的一个核心概念——矩阵秩——至关重要。在线性回归中,秩揭示了特征的线性独立性。本质上,任何特征都不应是另一个特征的直接线性组合。这种独立性至关重要,因为特征之间的依赖性——其中秩小于特征数量——会导致完美多重共线性。这种情况会扭曲回归模型的可解释性和可靠性,影响其在制定明智决策方面的效用。
让我们以 Ames Housing 数据集为例进行探讨。我们将检查数据集的秩和特征数量以检测多重共线性。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 导入必要的库来检查和比较列数与数据集的秩 import pandas as pd import numpy as np # 加载数据集 Ames = pd.read_csv('Ames.csv') # 选择不含缺失值的数值列 numerical_data = Ames.select_dtypes(include=[np.number]).dropna(axis=1) # 计算矩阵秩 rank = np.linalg.matrix_rank(numerical_data.values) # 特征数量 num_features = numerical_data.shape[1] # 打印秩和特征数量 print(f"不含缺失值的数值特征数量:{num_features}") print(f"秩:{rank}") |
我们的初步结果表明,Ames Housing 数据集存在多重共线性,有 27 个特征但秩只有 26。
|
1 2 |
不含缺失值的数值特征数量:27 秩:26 |
为解决此问题,让我们使用定制函数来识别冗余特征。此方法有助于就特征选择或修改做出明智的决定,以增强模型的可靠性和可解释性。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# 创建并使用一个函数来识别数据集中冗余的特征 import pandas as pd import numpy as np def find_redundant_features(data): """ 根据矩阵秩识别并返回数据集中冗余的特征。 当移除一个特征不会降低数据集的秩时,该特征就被认为是冗余的, 这表明它可以表示为其他特征的线性组合。 参数 data (DataFrame): 要分析的数值数据集。 返回 list: 冗余特征名称的列表。 """ # 计算原始数据集的矩阵秩 original_rank = np.linalg.matrix_rank(data) redundant_features = [] for column in data.columns: # 创建一个不包含此列的新数据集 temp_data = data.drop(column, axis=1) # 计算新数据集的秩 temp_rank = np.linalg.matrix_rank(temp_data) # 如果秩没有降低,则移除的列是冗余的 if temp_rank == original_rank: redundant_features.append(column) return redundant_features # 使用数值数据调用函数 Ames = pd.read_csv('Ames.csv') numerical_data = Ames.select_dtypes(include=[np.number]).dropna(axis=1) redundant_features = find_redundant_features(numerical_data) print("冗余特征:", redundant_features) |
以下特征被确定为冗余,表明它们对模型的预测能力没有独特贡献。
|
1 |
冗余特征:['GrLivArea', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF'] |
在识别出数据集中的冗余特征后,理解其冗余的性质至关重要。具体来说,我们怀疑“GrLivArea”可能只是“1stFlrSF”、“2ndFlrSF”以及“LowQualFinSF”的总和。为验证这一点,我们将计算这三个面积的总和,并将其直接与“GrLivArea”进行比较,以确认它们是否确实相同。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 导入 pandas import pandas as pd # 加载数据集 Ames = pd.read_csv('Ames.csv') # 计算 '1stFlrSF'、'2ndFlrSF' 和 'LowQualFinSF' 的总和 Ames['CalculatedGrLivArea'] = Ames['1stFlrSF'] + Ames['2ndFlrSF'] + Ames['LowQualFinSF'] # 将计算出的总和与现有的“GrLivArea”列进行比较,以查看它们是否相同 Ames['IsEqual'] = Ames['GrLivArea'] == Ames['CalculatedGrLivArea'] # 输出值匹配的行百分比 match_percentage = Ames['IsEqual'].mean() * 100 print(f"GrLivArea 等于其他三个特征总和的行百分比:{int(match_percentage)}%") |
我们的分析证实,“GrLivArea”在数据集中 100% 的情况下精确地是“1stFlrSF”、“2ndFlrSF”和“LowQualFinSF”的总和。
|
1 |
GrLivArea 等于其他三个特征总和的行百分比:100% |
在通过矩阵秩分析确定“GrLivArea”的冗余性之后,我们现在旨在可视化多重共线性对我们回归模型稳定性和预测能力的影响。接下来的步骤将包括使用冗余特征运行多元线性回归,以观察系数估计值的方差。此练习将有助于以切实可行的方式演示多重共线性的实际影响,从而强化在模型构建中仔细进行特征选择的必要性。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
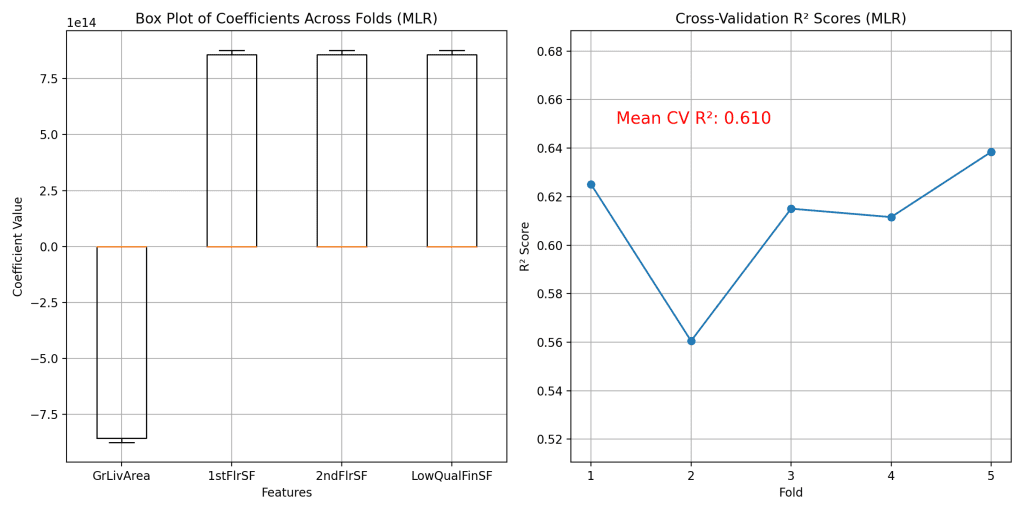
# 导入必要的库 import numpy as np import pandas as pd 来自 sklearn.linear_model 导入 LinearRegression from sklearn.model_selection import KFold import matplotlib.pyplot as plt # 加载数据 Ames = pd.read_csv('Ames.csv') features = ['GrLivArea', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF'] X = Ames[features] y = Ames['SalePrice'] # 初始化 K 折交叉验证 kf = KFold(n_splits=5, shuffle=True, random_state=1) # 收集系数和交叉验证得分 coefficients = [] cv_scores = [] for train_index, test_index in kf.split(X): X_train, X_test = X.iloc[train_index], X.iloc[test_index] y_train, y_test = y.iloc[train_index], y.iloc[test_index] # 初始化并拟合线性回归模型 model = LinearRegression() model.fit(X_train, y_train) coefficients.append(model.coef_) # 使用模型的 score 方法计算 R^2 分数 score = model.score(X_test, y_test) # print(score) cv_scores.append(score) # 绘制系数图 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.boxplot(np.array(coefficients), labels=features) plt.title('交叉验证时系数箱线图(MLR)') plt.xlabel('特征') plt.ylabel('系数取值') plt.grid(True) # 绘制交叉验证得分图 plt.subplot(1, 2, 2) plt.plot(range(1, 6), cv_scores, marker='o', linestyle='-') # 将 x 轴调整为从 1 开始 plt.title('交叉验证 R² 分数(MLR)') plt.xlabel('折') plt.xticks(range(1, 6)) # 设置 x 轴刻度以匹配折编号 plt.ylabel('R² 分数') plt.ylim(min(cv_scores) - 0.05, max(cv_scores) + 0.05) # 动态调整 y 轴限制 plt.grid(True) # 注释平均 R² 分数 mean_r2 = np.mean(cv_scores) plt.annotate(f'平均 CV R²:{mean_r2:.3f}', xy=(1.25, 0.65), color='red', fontsize=14), plt.tight_layout() plt.show() |
结果可以通过下面的两个图来展示。
左侧的箱线图说明了系数估计值的显著方差。这些值的大量分布不仅表明了我们模型的不稳定性,而且直接挑战了其可解释性。多元线性回归因其可解释性而备受推崇,而可解释性取决于其系数的稳定性和一致性。当系数在不同数据子集之间差异很大时,就很难获得清晰可行的见解,而这些见解对于根据模型预测做出明智的决策至关重要。鉴于这些挑战,需要一种更鲁棒的方法来解决模型系数的可变性和不稳定性。
想开始学习进阶数据科学吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
使用 Lasso 回归处理多重共线性
Lasso 回归提供了一种鲁棒的解决方案。与多元线性回归不同,Lasso 可以惩罚系数的大小,更重要的是,可以将某些系数设置为零,从而有效地减少模型中的特征数量。此特征选择在缓解多重共线性方面尤其有益。让我们将 Lasso 应用于之前的示例来演示这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
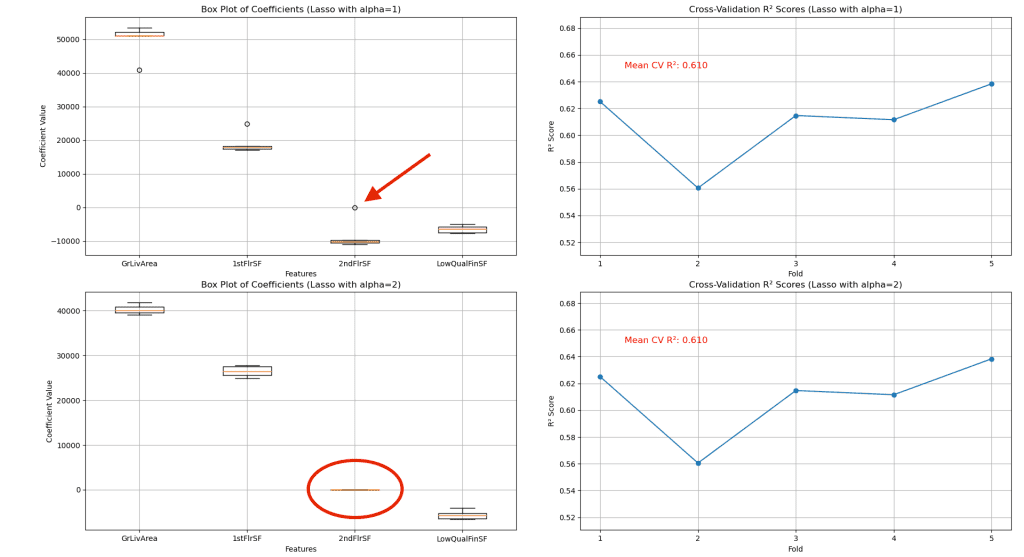
# 导入必要的库 import numpy as np import pandas as pd 来自 sklearn.linear_model 导入 Lasso from sklearn.preprocessing import StandardScaler from sklearn.model_selection import KFold import matplotlib.pyplot as plt # 加载数据 Ames = pd.read_csv('Ames.csv') features = ['GrLivArea', '1stFlrSF', '2ndFlrSF', 'LowQualFinSF'] X = Ames[features] y = Ames['SalePrice'] # 初始化 K 折交叉验证 kf = KFold(n_splits=5, shuffle=True, random_state=1) # 准备收集结果 results = {} for alpha in [1, 2]: # 循环遍历两个 alpha 值 coefficients = [] cv_scores = [] for train_index, test_index in kf.split(X): X_train, X_test = X.iloc[train_index], X.iloc[test_index] y_train, y_test = y.iloc[train_index], y.iloc[test_index] # 标准化特征 scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # 初始化并拟合 Lasso 回归模型 lasso_model = Lasso(alpha=alpha, max_iter=20000) lasso_model.fit(X_train_scaled, y_train) coefficients.append(lasso_model.coef_) # 使用模型的 score 方法计算 R^2 分数 score = lasso_model.score(X_test_scaled, y_test) cv_scores.append(score) results[alpha] = (coefficients, cv_scores) # 绘制结果 fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(12, 12)) alphas = [1, 2] for i, alpha in enumerate(alphas): coefficients, cv_scores = results[alpha] # 绘制系数图 axes[i, 0].boxplot(np.array(coefficients), labels=features) axes[i, 0].set_title(f'系数箱线图(Lasso,alpha={alpha})') axes[i, 0].set_xlabel('特征') axes[i, 0].set_ylabel('系数取值') axes[i, 0].grid(True) # 绘制交叉验证得分图 axes[i, 1].plot(range(1, 6), cv_scores, marker='o', linestyle='-') axes[i, 1].set_title(f'交叉验证 R² 分数(Lasso,alpha={alpha})') axes[i, 1].set_xlabel('折') axes[i, 1].set_xticks(range(1, 6)) axes[i, 1].set_ylabel('R² 分数') axes[i, 1].set_ylim(min(cv_scores) - 0.05, max(cv_scores) + 0.05) axes[i, 1].grid(True) mean_r2 = np.mean(cv_scores) axes[i, 1].annotate(f'平均交叉验证 R²: {mean_r2:.3f}', xy=(1.25, 0.65), color='red', fontsize=12) plt.tight_layout() plt.show() |
通过改变正则化强度(alpha),我们可以观察到增加惩罚项如何影响系数以及模型的预测准确性。
左侧的箱线图显示,随着 alpha 的增加,系数的分布范围和幅度减小,表明估计值更稳定。值得注意的是,当 alpha 设置为 1 时,'2ndFlrSF' 的系数开始接近于零,而在 alpha 增加到 2 时,系数几乎为零。这种趋势表明,随着正则化强度的提高,'2ndFlrSF' 对模型的贡献最小,这可能意味着它与其他特征存在冗余或多重共线性。这种稳定是 Lasso 能够减少不重要特征影响的直接结果,这些特征很可能导致多重共线性。
‘2ndFlrSF’ 在对模型预测能力影响最小的情况下被移除,这一点很重要。它强调了 Lasso 在识别和消除不必要预测变量方面的效率。重要的是,即使该特征被有效置零,模型的整体可预测性也保持不变,这表明 Lasso 在保持模型性能的同时简化其复杂性方面非常稳健。
利用 Lasso 回归的见解完善线性回归模型
根据 Lasso 回归获得的见解,我们通过移除 ‘2ndFlrSF’(一个被确定为对预测能力贡献最小的特征)来优化了我们的模型。本节使用仅包含 ‘GrLivArea’、‘1stFlrSF’ 和 ‘LowQualFinSF’ 的修改后模型来评估其性能和系数稳定性。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
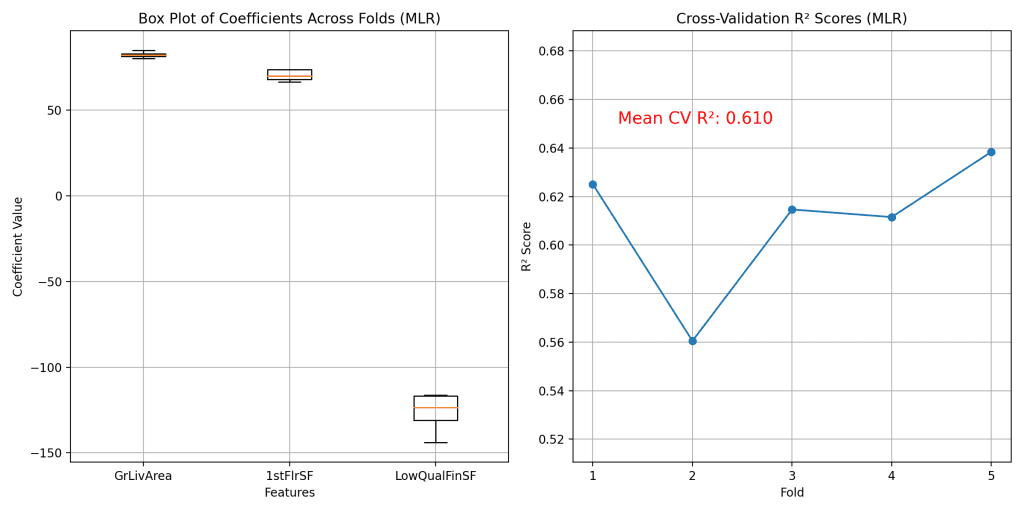
import matplotlib.pyplot as plt import numpy as np import pandas as pd 来自 sklearn.linear_model 导入 LinearRegression from sklearn.model_selection import KFold # 加载数据 Ames = pd.read_csv('Ames.csv') features = ['GrLivArea', '1stFlrSF', 'LowQualFinSF'] # 运行 Lasso 后移除 '2ndFlrSF' X = Ames[features] y = Ames['SalePrice'] # 初始化 K 折交叉验证 kf = KFold(n_splits=5, shuffle=True, random_state=1) # 收集系数和交叉验证得分 coefficients = [] cv_scores = [] for train_index, test_index in kf.split(X): X_train, X_test = X.iloc[train_index], X.iloc[test_index] y_train, y_test = y.iloc[train_index], y.iloc[test_index] # 初始化并拟合线性回归模型 model = LinearRegression() model.fit(X_train, y_train) coefficients.append(model.coef_) # 使用模型的 score 方法计算 R^2 分数 score = model.score(X_test, y_test) # print(score) cv_scores.append(score) # 绘制系数图 plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.boxplot(np.array(coefficients), labels=features) plt.title('交叉验证时系数箱线图(MLR)') plt.xlabel('特征') plt.ylabel('系数取值') plt.grid(True) # 绘制交叉验证得分图 plt.subplot(1, 2, 2) plt.plot(range(1, 6), cv_scores, marker='o', linestyle='-') # 将 x 轴调整为从 1 开始 plt.title('交叉验证 R² 分数(MLR)') plt.xlabel('折') plt.xticks(range(1, 6)) # 设置 x 轴刻度以匹配折编号 plt.ylabel('R² 分数') plt.ylim(min(cv_scores) - 0.05, max(cv_scores) + 0.05) # 动态调整 y 轴限制 plt.grid(True) # 注释平均 R² 分数 mean_r2 = np.mean(cv_scores) plt.annotate(f'平均 CV R²:{mean_r2:.3f}', xy=(1.25, 0.65), color='red', fontsize=14), plt.tight_layout() plt.show() |
我们的优化后的多元回归模型的计算结果将在下面的两个图中展示。
左侧的箱线图展示了系数在不同交叉验证折中的分布。值得注意的是,与包含“2ndFlrSF”的先前模型相比,系数的方差似乎有所减小。这种变异性的降低突显了移除冗余特征的有效性,这有助于稳定模型的估计并增强其可解释性。每个特征的系数现在表现出更小的波动,这表明模型可以在数据的不同子集上一致地评估这些特征的重要性。
除了保持模型的预测能力外,特征复杂性的降低还显著增强了模型的可解释性。由于变量数量的减少,每个变量都对结果做出独特贡献,我们现在可以更轻松地衡量这些特定特征对销售价格的影响。这种清晰性使得解释更加直接,并基于模型的输出做出更自信的决策。利益相关者可以更好地理解“GrLivArea”、“1stFlrSF”和“LowQualFinSF”的变化如何可能影响房产价值,从而实现更清晰的沟通和更可操作的见解。这种增强的透明度非常有价值,尤其是在那些解释模型预测与预测本身同等重要的领域。
进一步阅读
API
教程
Ames 住房数据集和数据字典
总结
这篇博文解决了回归模型中完美多重共线性的挑战,首先使用 Ames Housing 数据集的矩阵秩分析进行检测。然后,我们探索了 Lasso 回归,通过减少特征数量、稳定系数估计和保持模型预测性来缓解多重共线性。最后,通过战略性地减少特征,优化了线性回归模型,并增强了其可解释性和可靠性。
具体来说,你学到了:
- 使用矩阵秩分析检测数据集中完美的共线性。
- 应用 Lasso 回归来缓解多重共线性并协助特征选择。
- 通过 Lasso 的见解优化线性回归模型,以增强可解释性。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。







暂无评论。