如何在 Python 中使用 ARCH 和 GARCH 模型为时间序列预测建模波动性

作者 Jason Brownlee 于 2019 年 8 月 21 日发布在时间序列 95

方差或波动率随时间的变化，在使用 ARIMA 等经典方法对时间序列进行建模时，可能会导致问题。

ARCH 或自回归条件异方差方法，提供了一种对时间序列中随时间变化的方差进行建模的方法，例如增加或减少的波动率。该方法的一个扩展名为 GARCH 或广义自回归条件异方差，允许该方法支持时间相关波动率的变化，例如同一序列中增加和减少的波动率。

在本教程中，您将了解用于预测时间序列方差的 ARCH 和 GARCH 模型。

完成本教程后，您将了解：

时间序列中的方差问题以及对 ARCH 和 GARCH 模型的需求。
如何配置 ARCH 和 GARCH 模型。
如何在 Python 中实现 ARCH 和 GARCH 模型。

开始您的项目，请阅读我的新书《Python 时间序列预测入门》，其中包含分步教程以及所有示例的Python 源代码文件。

让我们开始吧。

How to Develop ARCH and GARCH Models for Time Series Forecasting in Python

如何在 Python 中为时间序列预测开发 ARCH 和 GARCH 模型
照片来源：Murray Foubister，保留部分权利。

教程概述

本教程分为五个部分；它们是：

方差问题
什么是 ARCH 模型？
什么是 GARCH 模型？
如何配置 ARCH 和 GARCH 模型
Python 中的 ARCH 和 GARCH 模型

方差问题

可以为单变量时间序列数据开发自回归模型，这些数据是平稳的（AR），有趋势（ARIMA）或有季节性成分（SARIMA）。

单变量时间序列的这些自回归模型未建模的一个方面是方差随时间的变化。

传统上，方差变化适中的时间序列有时可以通过幂变换进行调整，例如通过对数取对数或使用 Box-Cox 变换。

有些时间序列的方差会随着时间系统地变化。在金融领域的时间序列中，这将被称为增加和减少的波动率。

在方差以系统方式增加的时间序列中，例如趋势增加，该序列的这种特性称为异方差。这是统计学中的一个专业术语，意思是序列中的变化或不相等的方差。

如果方差的变化可以随时间相关，那么可以使用自回归过程来建模，例如 ARCH。

什么是 ARCH 模型？

自回归条件异方差（ARCH）是一种明确对时间序列中方差随时间的变化进行建模的方法。

具体来说，ARCH 方法将一个时间步的方差建模为平均过程（例如零均值）的残差误差的函数。

Engle（1982）引入的 ARCH 过程明确认识到无条件方差和条件方差之间的区别，允许后者随时间变化，作为过去误差的函数。

— 广义自回归条件异方差，1986 年。

必须指定一个滞后参数来定义包含在模型中的先前残差误差的数量。使用 GARCH 模型（稍后讨论）的表示法，我们可以将此参数称为“q”。最初，此参数称为“p”，在教程后面使用的 arch Python 包中也称为“p”。

q：包含在 ARCH 模型中的滞后平方残差误差的数量。

ARCH 模型的一个普遍接受的表示法是用滞后参数 q 调用 ARCH() 函数，例如 ARCH(1) 表示一阶 ARCH 模型。

该方法期望序列是平稳的，除了方差的变化之外，这意味着它没有趋势或季节性成分。ARCH 模型用于预测未来时间步的方差。

[ARCH] 是均值为零、序列不相关、条件方差随过去而变化但无条件方差恒定的过程。对于这些过程，近期过去提供了关于单周期预测方差的信息。

– 自回归条件异方差与英国通货膨胀方差的估计，1982 年。

实践中，这可以用于为使用 ARMA 或类似模型等自回归模型之后的残差方差建模。

该模型应仅应用于预白化残差序列 {e_t}，该序列是不相关的，并且不包含趋势或季节性变化，例如在拟合满意的 SARIMA 模型后获得的序列。

— 第 148 页，《R 语言时间序列入门》，2009 年。

什么是 GARCH 模型？

广义自回归条件异方差（GARCH）是 ARCH 模型的一个扩展，它结合了移动平均分量和自回归分量。

具体来说，该模型包括滞后方差项（例如，如果对另一个过程的白噪声残差进行建模，则为观测值），以及来自平均过程的滞后残差误差。

引入移动平均分量可以使模型同时建模方差随时间的条件变化以及时间相关方差的变化。例如，条件方差的增加和减少。

因此，该模型引入了一个新参数“p”，该参数描述了滞后方差项的数量。

p：包含在 GARCH 模型中的滞后方差数量。
q：包含在 GARCH 模型中的滞后残差误差数量。

GARCH 模型的一个普遍接受的表示法是用滞后参数 p 和 q 调用 GARCH() 函数，例如 GARCH(1, 1) 表示一阶 GARCH 模型。

GARCH 模型包含 ARCH 模型，其中 GARCH(0, q) 等同于 ARCH(q) 模型。

当 p = 0 时，该过程简化为 ARCH(q) 过程，而当 p = q = 0 时，E(t) 仅为白噪声。在 ARCH(q) 过程中，条件方差被指定为过去样本方差的线性函数，而 GARCH(p, q) 过程允许滞后条件方差也进入。这对应于某种自适应学习机制。

— 广义自回归条件异方差，1986 年。

与 ARCH 类似，GARCH 预测未来方差，并期望序列是平稳的，除了方差的变化之外，这意味着它没有趋势或季节性成分。

如何配置 ARCH 和 GARCH 模型

ARCH 模型的配置最好在时间序列方差的 ACF 和 PACF 图的背景下理解。

这可以通过从序列的每个观测值中减去均值并对其结果进行平方来实现，或者如果您已经在处理来自另一个模型的白噪声残差，则只需对其进行平方。

如果相关图看起来像白噪声 [...]，那么可以通过查看平方值的相关图来检测波动率，因为平方值等同于方差（前提是序列已调整为均值为零）。

— 第 146-147 页，《R 语言时间序列入门》，2009 年。

ACF 和 PACF 图随后可以以与 ARMA 模型类似的方式进行解释，以估计 p 和 q 的值。

有关如何执行此操作的更多信息，请参阅此帖

自相关与偏自相关入门指南

Python 中的 ARCH 和 GARCH 模型

在本节中，我们将介绍如何使用arch 库在 Python 中开发 ARCH 和 GARCH 模型。

首先，让我们准备一个可用于这些示例的数据集。

测试数据集

我们可以创建一个具有受控方差模型的数据集。

最简单的情况是随机噪声序列，其均值为零，方差从 0.0 开始稳步增加。

我们可以使用gauss() 函数在 Python 中实现这一点，该函数生成具有指定均值和标准差的高斯随机数。

# create dataset
data = [gauss(0, i*0.01) for i in range(1,100+1)]

1 2	# 创建数据集 data = [gauss(0, i*0.01) for i in range(1,100+1)]

我们可以绘制数据集以了解线性方差变化的外观。完整的示例列在下面。

# create a simple white noise with increasing variance
from random import gauss
from random import seed
from matplotlib import pyplot
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# plot
pyplot.plot(data)
pyplot.show()

# 创建一个方差递增的简单白噪声

from random import gauss

from random import seed

from matplotlib import pyplot

# 种子伪随机数生成器

seed(1)

# 创建数据集

data = [gauss(0, i*0.01) for i in range(0,100)]

# 绘图

pyplot.plot(data)

pyplot.show()

运行示例会创建并绘制数据集。我们可以看到序列过程中方差的明显变化。

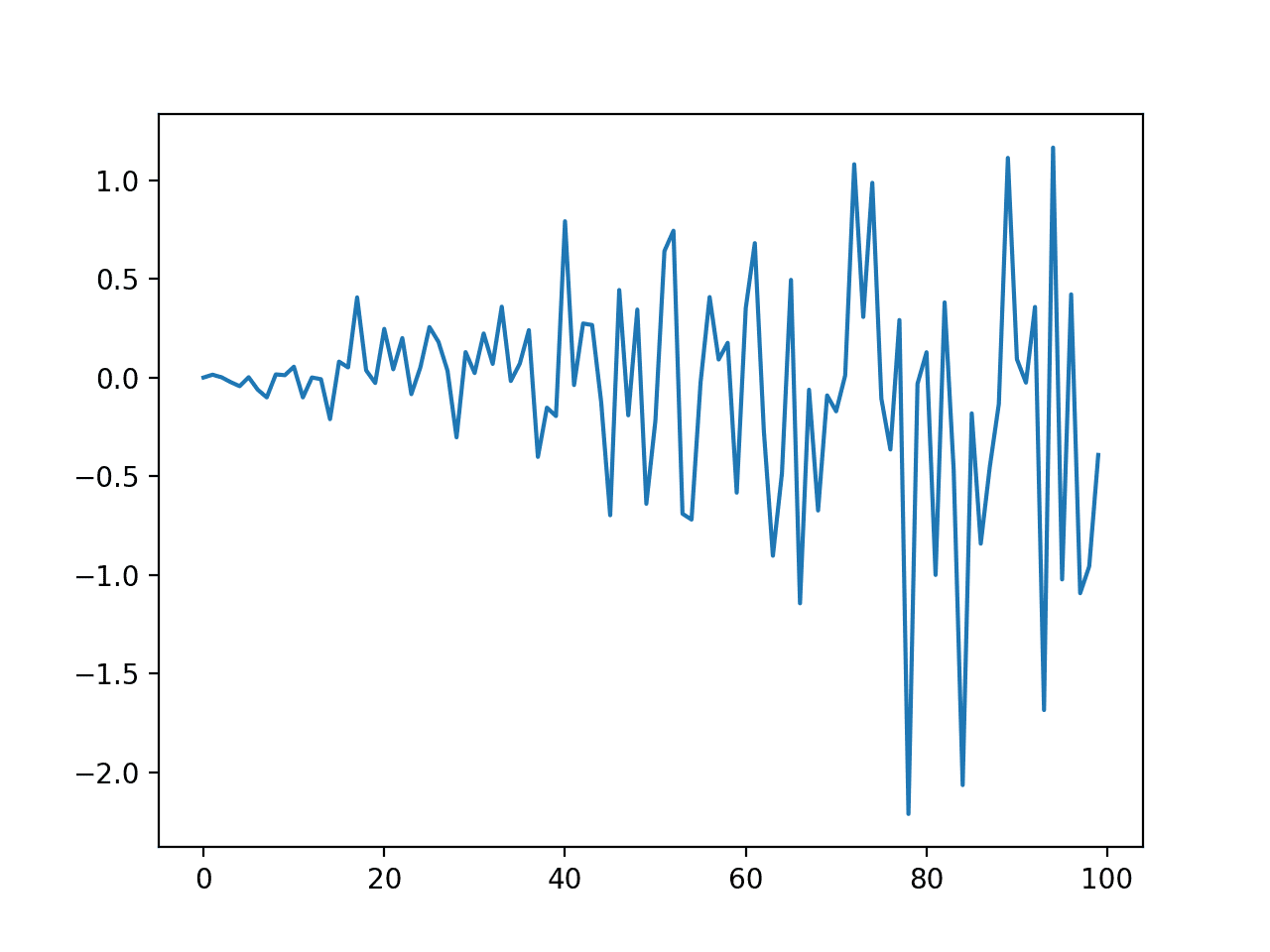
Line Plot of Dataset with Increasing Variance

具有递增方差的数据集折线图

自相关

我们知道我们构造的数据集的方差存在自相关。

尽管如此，我们可以查看自相关图来确认这一预期。完整的示例列在下面。

# check correlations of squared observations
from random import gauss
from random import seed
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# square the dataset
squared_data = [x**2 for x in data]
# create acf plot
plot_acf(squared_data)
pyplot.show()

# 检查平方观测值的相关性

from random import gauss

from random import seed

from matplotlib import pyplot

from statsmodels.graphics.tsaplots import plot_acf

# 种子伪随机数生成器

seed(1)

# 创建数据集

data = [gauss(0, i*0.01) for i in range(0,100)]

# 平方数据集

squared_data = [x**2 for x in data]

# 创建 ACF 图

plot_acf(squared_data)

pyplot.show()

运行示例会创建平方观测值的自相关图。我们看到方差在长达约 15 个滞后时间步内存在显著的正相关。

这可能是 ARCH 模型中参数的一个合理值。

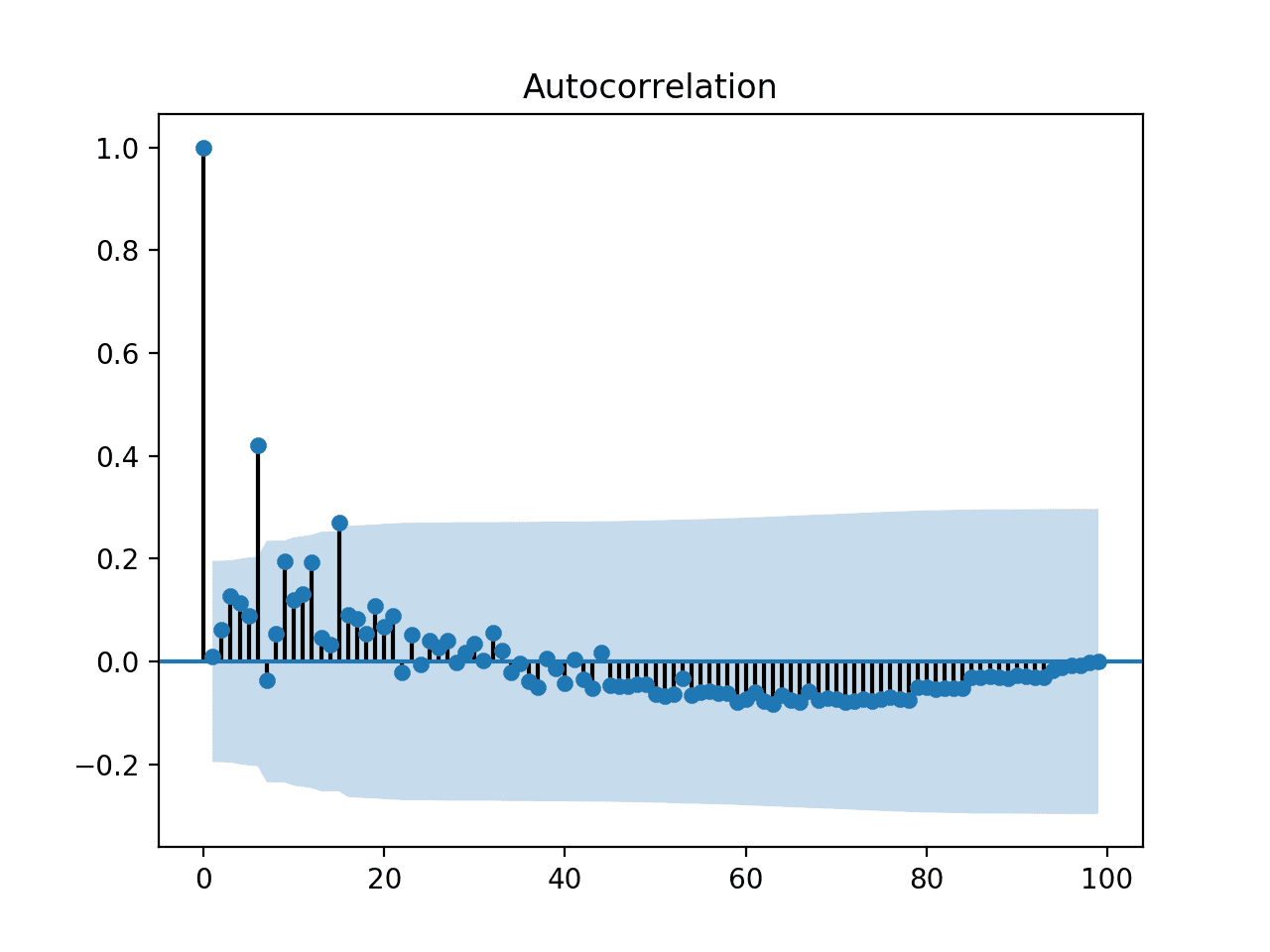
Autocorrelation Plot of Data with Increasing Variance

具有递增方差的数据的自相关图

ARCH 模型

开发 ARCH 模型涉及三个步骤：

定义模型
拟合模型
进行预测。

在拟合和预测之前，我们可以将数据集分成训练集和测试集，以便我们可以在训练集上拟合模型并评估其在测试集上的性能。

# split into train/test
n_test = 10
train, test = data[:-n_test], data[-n_test:]

# 分割成训练/测试集

n_test = 10

train, test = data[:-n_test], data[-n_test:]

可以通过调用arch_model() 函数来定义模型。我们可以为序列的均值指定一个模型：在这种情况下，mean='Zero' 是一个合适的模型。然后我们可以为方差指定模型：在这种情况下，vol='ARCH'。我们还可以为 ARCH 模型指定滞后参数：在这种情况下，p=15。

注意，在 arch 库中，ARCH/GARCH 的 p 和 q 参数名称已互换。

# define model
model = arch_model(train, mean='Zero', vol='ARCH', p=15)

1 2	# 定义模型 model = arch_model(train, mean='Zero', vol='ARCH', p=15)

通过调用fit() 函数可以在数据上拟合模型。此函数有许多选项，但默认值已足够开始使用。这将返回一个拟合模型。

# fit model
model_fit = model.fit()

1 2	# 拟合模型 model_fit = model.fit()

最后，我们可以通过在拟合模型上调用forecast() 函数来进行预测。我们可以指定预测的范围。

在本例中，我们将预测数据集中最后 10 个时间步的方差，并将其从模型训练中排除。

# forecast the test set
yhat = model_fit.forecast(horizon=n_test)

1 2	# 预测测试集 yhat = model_fit.forecast(horizon=n_test)

我们可以将所有这些结合起来；完整的示例如下所示。

# example of ARCH model
from random import gauss
from random import seed
from matplotlib import pyplot
from arch import arch_model
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# split into train/test
n_test = 10
train, test = data[:-n_test], data[-n_test:]
# define model
model = arch_model(train, mean='Zero', vol='ARCH', p=15)
# fit model
model_fit = model.fit()
# forecast the test set
yhat = model_fit.forecast(horizon=n_test)
# plot the actual variance
var = [i*0.01 for i in range(0,100)]
pyplot.plot(var[-n_test:])
# plot forecast variance
pyplot.plot(yhat.variance.values[-1, :])
pyplot.show()

# ARCH 模型示例

from random import gauss

from random import seed

from matplotlib import pyplot

from arch import arch_model

# 种子伪随机数生成器

seed(1)

# 创建数据集

data = [gauss(0, i*0.01) for i in range(0,100)]

# 分割成训练/测试集

n_test = 10

train, test = data[:-n_test], data[-n_test:]

# 定义模型

model = arch_model(train, mean='Zero', vol='ARCH', p=15)

# 拟合模型

model_fit = model.fit()

# 预测测试集

yhat = model_fit.forecast(horizon=n_test)

# 绘制实际方差

var = [i*0.01 for i in range(0,100)]

pyplot.plot(var[-n_test:])

# 绘制预测方差

pyplot.plot(yhat.variance.values[-1, :])

pyplot.show()

运行示例会定义并拟合模型，然后预测数据集中最后 10 个时间步的方差。

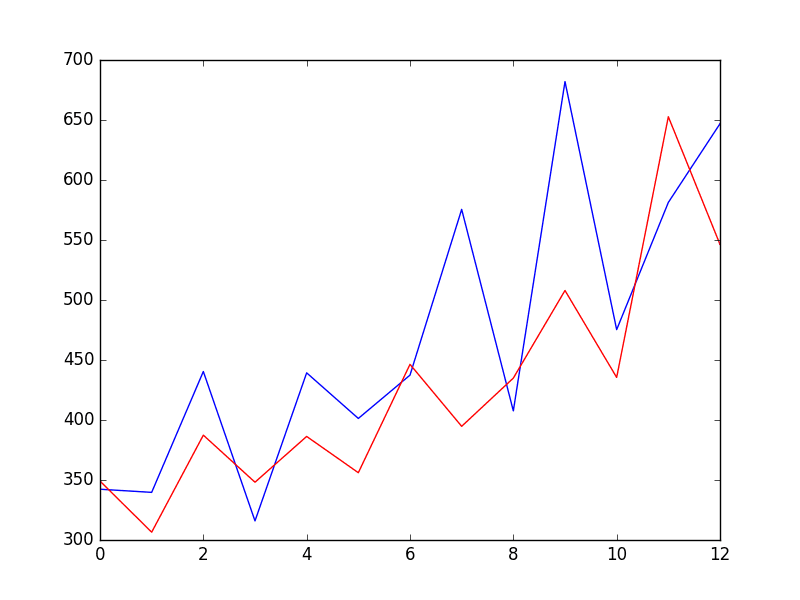
创建折线图来比较期望方差与预测方差。尽管模型没有经过调优，但预测的方差看起来是合理的。

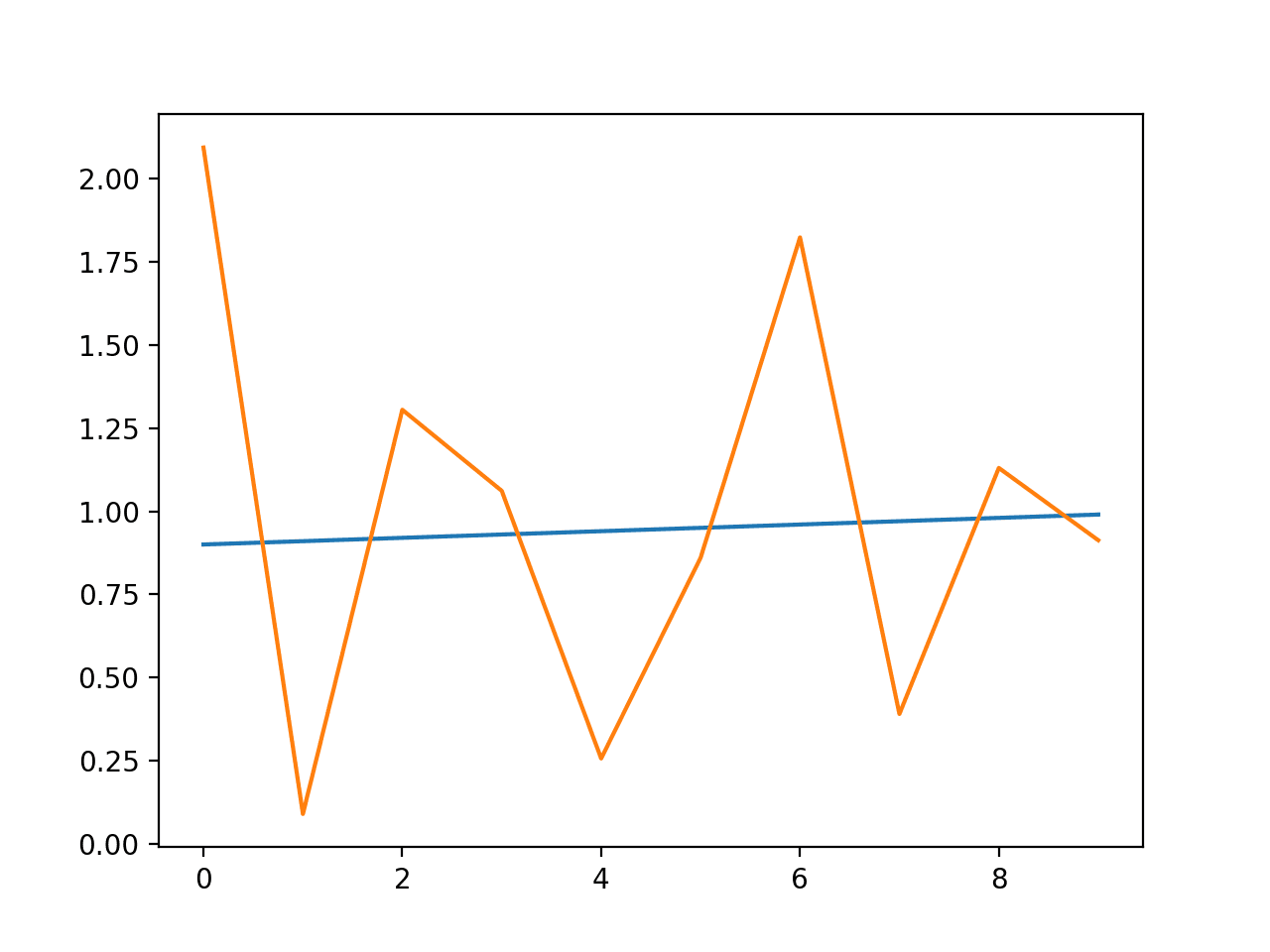
Line Plot of Expected Variance to Predicted Variance using ARCH

使用 ARCH 预测方差与期望方差的折线图

GARCH 模型

使用 arch 库也可以轻松拟合 GARCH 模型。

arch_model() 函数可以指定 GARCH 而非 ARCH 模型 vol='GARCH'，以及两者的滞后参数。

# define model
model = arch_model(train, mean='Zero', vol='GARCH', p=15, q=15)

1 2	# 定义模型 model = arch_model(train, mean='Zero', vol='GARCH', p=15, q=15)

鉴于线性增加的方差，该数据集可能不适合 GARCH 模型，但完整的示例仍列在下面。

# example of ARCH model
from random import gauss
from random import seed
from matplotlib import pyplot
from arch import arch_model
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# split into train/test
n_test = 10
train, test = data[:-n_test], data[-n_test:]
# define model
model = arch_model(train, mean='Zero', vol='GARCH', p=15, q=15)
# fit model
model_fit = model.fit()
# forecast the test set
yhat = model_fit.forecast(horizon=n_test)
# plot the actual variance
var = [i*0.01 for i in range(0,100)]
pyplot.plot(var[-n_test:])
# plot forecast variance
pyplot.plot(yhat.variance.values[-1, :])
pyplot.show()

# ARCH 模型示例

from random import gauss

from random import seed

from matplotlib import pyplot

from arch import arch_model

# 种子伪随机数生成器

seed(1)

# 创建数据集

data = [gauss(0, i*0.01) for i in range(0,100)]

# 分割成训练/测试集

n_test = 10

train, test = data[:-n_test], data[-n_test:]

# 定义模型

model = arch_model(train, mean='Zero', vol='GARCH', p=15, q=15)

# 拟合模型

model_fit = model.fit()

# 预测测试集

yhat = model_fit.forecast(horizon=n_test)

# 绘制实际方差

var = [i*0.01 for i in range(0,100)]

pyplot.plot(var[-n_test:])

# 绘制预测方差

pyplot.plot(yhat.variance.values[-1, :])

pyplot.show()

下面列出了期望方差和预测方差的图。

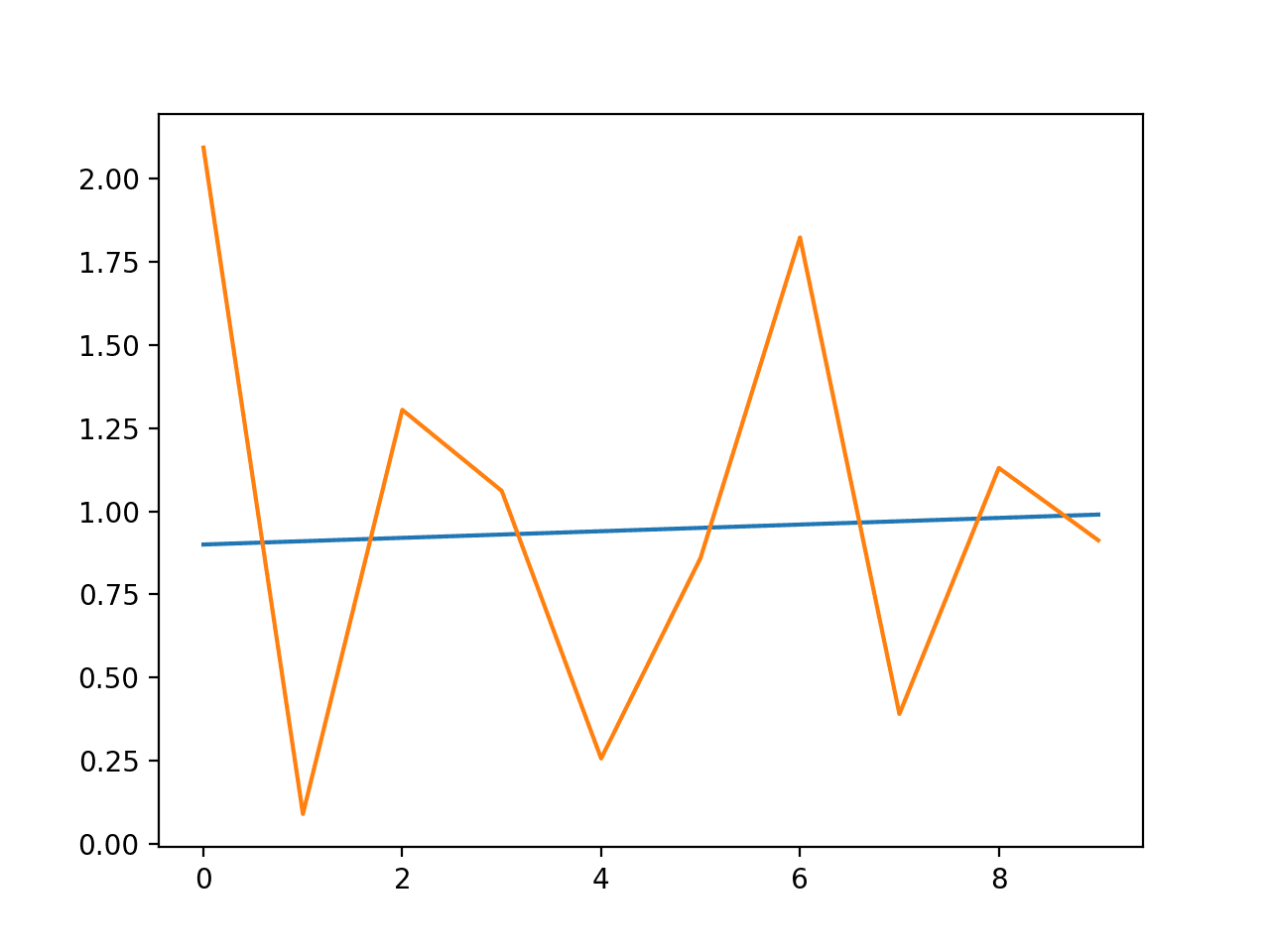
Line Plot of Expected Variance to Predicted Variance using GARCH

使用 GARCH 预测方差与期望方差的折线图

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

论文和书籍

API

文章

总结

在本教程中，您了解了用于预测时间序列方差的 ARCH 和 GARCH 模型。

具体来说，你学到了：

时间序列中的方差问题以及对 ARCH 和 GARCH 模型的需求。
如何配置 ARCH 和 GARCH 模型。
如何在 Python 中实现 ARCH 和 GARCH 模型。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

时间序列预测的 4 种常见机器学习数据变换

使用脑电波预测一个人眼睛是睁开还是闭合

95 条回复关于“如何在 Python 中为时间序列预测开发 ARCH 和 GARCH 模型”

Elie Kawerk 2018 年 8 月 24 日上午 6:26 #

嗨，Jason，

您提到了 PACF 的需求，但没有绘制它，难道不需要 PACF 来确定 q 吗？

祝好，
Elie K

回复
- Jason Brownlee 2018 年 8 月 24 日上午 9:15 #
  
  是的，您可以使用 ACF 和 PACF，在此了解更多信息
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  回复
- Mahmoud 2023 年 6 月 29 日凌晨 12:42 #
  
  嗨 Eile，我认为 pacf 用于确定“p”的值而不是“q”
  
  回复
Anthony The Koala 2018 年 8 月 25 日晚上 11:46 #

当您谈论预测模型方差时，方差不是标准差的平方吗？但在您的代码的第 9 行，无论 ARCH 还是 GARCH 模型，您都生成了均值和标准差的高斯数，而不是均值和标准差的平方。
您能否在本文的上下文中阐述一下标准差、标准差的平方和方差？
谢谢你
悉尼的Anthony

回复
- Jason Brownlee 2018 年 8 月 26 日上午 6:29 #
  
  构造的样本问题只是代码演示的一个背景。不要过分解读它。
  
  回复
Sebastian 2018 年 8 月 26 日凌晨 2:34 #

你好，Jason。
我认为您在这个博客上的工作很棒！

我有一个概念性问题。所以 ARCH 和 GARCH 并不适用于预测或预报时间序列的后续数据值，而是用于预测未来数据可能具有的方差？也就是说，在股票价格预测中，这些方法不会显示未来的价格，而是会显示那些未来价格可能暗示的方差？

非常感谢，

来自哥伦比亚的 Sebastián。

回复
- Jason Brownlee 2018 年 8 月 26 日上午 6:30 #
  
  将它们更多地视为序列变异性的模型。
  
  回复
Dhineshkumar R 2018 年 9 月 3 日上午 5:46 #

嗨，Jason，

再次感谢这个很棒的博客。

如果您能告诉我为什么我们计算平方残差的 ACF 而不是仅残差的 ACF，那将会有帮助。

谢谢。

回复
- Jason Brownlee 2018 年 9 月 3 日上午 6:17 #
  
  帖子中已提到。
  
  平方残差等同于方差（例如，我们正在建模的东西）。
  
  回复
Lesego 2018 年 9 月 13 日晚上 9:33 #

试图遵循教程，但在导入 arch_model 模块的步骤上卡住了。

我收到“No module named ‘arch'”错误，并且找不到在线解决方案来修复它。有什么帮助吗？

回复
- Jason Brownlee 2018 年 9 月 14 日上午 6:35 #
  
  您必须先安装包
  
  pip install arch
  
  1
  
  pip install arch
  
  更多帮助请点击此处
  https://github.com/bashtage/arch
  
  回复
yogesh 2018 年 10 月 10 日上午 5:03 #

嗨 Jason，我想知道这是否不用于预测或预报未来值，为什么还要用于方差？
我感到很困惑，请为我澄清。

回复
- Jason Brownlee 2018 年 10 月 10 日上午 6:17 #
  
  ARCH 模型仅在您想预测波动率而不是值时有用。
  
  回复
  - yogesh 2018 年 10 月 23 日下午 5:56 #
    
    好的，谢谢，但有没有办法用这些方差来预测值？
    
    回复
    - prof.yapper 2024 年 1 月 5 日上午 7:51 #
      
      您应该使用不同的模型来预测值
      
      回复
  - Muhammad khan 2019 年 4 月 17 日下午 2:23 #
    
    您好先生！我们使用哪种模型进行长期预测
    
    回复
    - Jason Brownlee 2019 年 4 月 17 日下午 2:46 #
      
      我建议您测试和评估一套模型，以发现最适合您特定数据集的模型。
      
      这可能有助于作为起点
      https://machinelearning.org.cn/how-to-develop-a-skilful-time-series-forecasting-model/
      
      回复
Sathya 2018 年 10 月 11 日晚上 10:46 #

嗨 Jason，您是如何得出 p=15 的。难道不是和您查看 ACF 和 PACF 图然后决定 p 和 q 的方式一样吗？在这种情况下，通常 p 和 q 应该小于 5，对吗？

回复
- Jason Brownlee 2018 年 10 月 12 日上午 6:40 #
  
  从帖子中
  
  我们看到方差在长达约 15 个滞后时间步内存在显著的正相关。
  
  回复
Mohamad Alkadri 2019 年 1 月 13 日凌晨 4:20 #

太棒了！

回复
- Jason Brownlee 2019 年 1 月 13 日上午 5:43 #
  
  谢谢，很高兴对您有帮助。
  
  回复
Tim 2019 年 1 月 25 日下午 12:46 #

这是一篇非常有用的帖子！我正在尝试弄清楚一些事情

1. 假设我们取一系列时间序列，例如每日波动率度量，并直接通过标准的ARIMA方法进行预测。这里可以进行差分处理，直到得到一个平稳序列。
2. 使用ARCH模型预测波动率。

在第一种方法中，差分处理不能解决方差非恒定的问题吗？另外，如果使用ARCH模型，是否必须先拟合一个AR类型的模型，然后再使用ARCH？或者波动率序列可以直接通过ARCH进行预测吗？

我对这些问题感到困惑，所以任何澄清都会有帮助。谢谢！

回复
- Jason Brownlee 2019年1月26日上午6:06 #
  
  差分不能解决方差变化的问题。它解决的是水平（趋势）变化。
  
  回复
  - Tim 2019年1月26日上午11:57 #
    
    那么，波动率序列不能通过标准的ARIMA模型进行预测吗？
    
    另外，ARCH模型是直接用于预测波动率序列吗？还是先用AR模型对股票价格进行建模，然后对残差使用ARCH？
    
    回复
    - Jason Brownlee 2019年1月27日上午7:38 #
      
      ARIMA可以用来预测，但它不是为此问题设计的。
      
      我不知道如何预测股票价格，抱歉。
      https://machinelearning.org.cn/faq/single-faq/can-you-help-me-with-machine-learning-for-finance-or-the-stock-market
      
      回复
Vikash 2019年2月4日晚上10:19 #

Jason您好！非常感谢您提供的优雅解决方案。我们能否使用GARCH模型来解决分类问题，其中因变量的类别对应于隐含波动率的条件？

回复
- Jason Brownlee 2019年2月5日上午8:22 #
  
  不行。
  
  回复
John Emeka 2019年2月18日下午7:45 #

医生您好……我正在研究尼日利亚某家商业银行突变情况下的GARCH建模，您能给我推荐一本参考书吗？

回复
- Jason Brownlee 2019年2月19日上午7:23 #
  
  或许可以从这里开始：https://scholar.google.com
  
  回复
Ajay 2019年3月31日上午10:24 #

博士您好，我是加拿大的一名经济学专业的学生。如果通过一些诊断检验发现我的ARMA模型存在异方差性，我是否可以使用ARCH或GARCH模型来解决异方差性问题？

回复
- Jason Brownlee 2019年4月1日上午7:45 #
  
  也许可以，但据我所知不行。
  
  回复
Marco 2019年4月17日下午6:29 #

那么，蓝线（最后两个图）是ARMA过程残差的方差估计，对吗？（您在这里人为创建的DATA变量是AR过程的残差吗？）感谢您的工作。
Marco

回复
- Jason Brownlee 2019年4月18日上午8:25 #
  
  这是对方差的模型和预测。
  
  回复
Tamir 2019年5月14日凌晨2:25 #

您好。

感谢这个例子。
我有一个练习，想知道您是否可以帮助我。
我想对CSV文件中的股票指数运行GARCH测试。
文件包含2列：日期和每日回报。

为了将其应用于我的数据，我需要更改示例中的哪些内容？

再次感谢。

回复
- Jason Brownlee 2019年5月14日上午7:50 #
  
  您可以在这里了解如何加载数据。
  https://machinelearning.org.cn/load-machine-learning-data-python/
  
  回复
Tamir 2019年5月23日晚上10:58 #

我已经成功上传了我的CSV文件，没有问题，但在尝试运行时出现了一个错误：
“model_fit = model.fit()”

如果您能帮助我，我将不胜感激。
我的完整脚本附在下面

#数据
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib import pyplot
mydataset= pd.read_csv(‘TLV 35.csv’)
x= pd.to_datetime(mydataset[‘Date’])
y= mydataset[‘R’]
mydataset.head()
plt.plot(x,y)
pyplot.show()

plt.xlabel(‘Date’)
plt.ylabel(‘R’)

from statsmodels.graphics.tsaplots import plot_acf
y= mydataset[‘R’]
data= mydataset

#自相关
from pandas import Series
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
series = Series.from_csv(‘TLV 35.csv’, header=1)
plot_acf(series)
pyplot.show()

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib import pyplot
import statsmodels.api as sm
import matplotlib
%matplotlib inline
df=pd.read_csv(‘TLV 35 with graph.csv’)
df.head()

df.columns=[‘date’,’R’]
df.head()
df[‘date’]= pd.to_datetime(df[‘date’])
df.head()
df.set_index(‘date’,inplace=True)
df.head()
df.index
df.describe().transpose()
df.plot()
time_series=df[‘R’]
type(time_series)
time_series.rolling(365).mean().plot(label=’moving av’)
time_series.rolling(365).std().plot(label=’moving std’)
time_series.plot()

from arch import arch_model
# 分割成训练/测试集
n_test = 10
train, test = df.index[:-n_test], df.index[-n_test:]
model=arch_model(train, mean=’zero’, vol=’ARCH’, p=1)

model_fit = model.fit()

回复
- Jason Brownlee 2019年5月24日上午7:52 #
  
  您收到的是什么错误？
  
  回复
Francisco Lopes 2019年5月27日上午11:56 #

AR(4)+GARCH(9,6)模型需要估计多少个参数？

回复
- Jason Brownlee 2019年5月27日下午2:38 #
  
  好问题，我认为这是可以知道的，我暂时无法为您计算，抱歉。
  
  回复
Jamshid Rizvi 2019年7月23日下午4:42 #

我使用ARDL边界检验估计了模型，现在正考虑将ARCH和GARCH应用于一个包含5个宏观变量的模型。请指导我是否可行。我的数据范围从1970-2018年。怎么做？？

回复
- Jason Brownlee 2019年7月24日上午7:51 #
  
  什么是ARDL？
  
  回复
karthi 2019年11月13日凌晨5:48 #

我已经成功上传了我的Excel文件，没有问题，但在尝试运行时出现了一个错误：

# 定义模型
model = arch_model(train, mean=’Zero’, vol=’GARCH’, p=10, q=10)

—————————————————————————

NameError Traceback (最近一次调用)
in
1 # 定义模型
—-> 2 model = arch_model(train, mean=’Zero’, vol=’GARCH’, p=15, q=15)

NameError: name ‘arch_model’ is not defined

回复
- Jason Brownlee 2019年11月13日凌晨5:53 #
  
  您可能跳过了一些导入函数的示例代码行。
  
  回复

ENRIQUE BONILLA 2020年2月1日上午5:08 #

Jason，精彩的教程！

一些针对Python 3.7的更新：

示例代码需要预先安装包：

sudo pip3 install arch
sudo pip3 install statsmodels

并在自相关示例代码中使用numpy，以下是已经测试过的新代码：

# check correlations of squared observations
from random import gauss
from random import seed
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
import numpy

# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# square the dataset
squared_data = numpy.array([x**2 for x in data])
# create acf plot
plot_acf(squared_data)
pyplot.show()

# 检查平方观测值的相关性

from random import gauss

from random import seed

from matplotlib import pyplot

from statsmodels.graphics.tsaplots import plot_acf

import numpy

# 种子伪随机数生成器

seed(1)

# 创建数据集

data = [gauss(0, i*0.01) for i in range(0,100)]

# 平方数据集

squared_data = numpy.array([x**2 for x in data])

# 创建 ACF 图

plot_acf(squared_data)

pyplot.show()

通过这些步骤，所有示例都能完美运行。

非常感谢您Jason发布的所有内容！
E. Bonilla

Jason Brownlee 2020年2月1日上午5:59 #

感谢分享。

回复
- LC 2020年12月1日下午12:14 #
  
  嘿，Jason，谢谢您这篇很棒的教程，Enrique，也谢谢您的更新。
  
  实际上，我在看到这篇评论之前，自己重写了代码，采用了与EB相同的 H 方式——但我来到评论区是为了找到解释，以解释输出结果与您在帖子中屏幕截图之间的差异。
  
  *问题：我的输出acf图显示y值的范围相同，x轴范围为0-20*
  
  而您的帖子显示x轴范围为0-100。
  
  想知道您或其他人是否能分享一些关于此事的见解？
  
  回复
  - Jason Brownlee 2020年12月1日下午1:20 #
    
    我认为API已经更改。
    
    我认为您可以通过函数的一个参数来更改滞后数。
    
    回复

Andrew 2020年2月4日凌晨5:55 #

感谢您的博客！

我能否从arch_model函数返回的表中检索系数（omega、alpha、beta）的值？

谢谢

回复
- Jason Brownlee 2020年2月4日上午8:01 #
  
  不客气。
  
  我认为系数就在模型内部，您可以使用API来检索它们。
  
  您可能需要深入研究ARCHModel类的代码。
  https://arch.readthedocs.io/en/latest/univariate/mean.html#arch.univariate.base.ARCHModel
  
  回复
moh abbas 2020年2月11日晚上10:49 #

这是一篇关于方差建模的简洁明了的文章，您是否有关于如何将其与其他模型（如ARIMA或VAR）结合以增强预测的示例？

回复
- Jason Brownlee 2020年2月12日上午5:46 #
  
  谢谢。
  
  还没有。
  
  回复
mark 2020年2月29日凌晨3:05 #

很棒的网站和帖子！假设我想对HMM-GARCH（RV=已实现波动率）进行建模，使用一个专有的状态相关变量（X）作为外部输入。HMM状态由X驱动……RV将以先前RV和当前X水平为条件。是否可以使用上述模型轻松实现这一点？即替换随机数据，并使用历史波动率和X？

再次感谢这篇帖子……非常有帮助；）

回复
- Jason Brownlee 2020年2月29日上午7:17 #
  
  谢谢。
  
  我不知道，抱歉。
  
  回复
Simon 2020年3月14日凌晨2:59 #

很好的解释，谢谢。
为什么您在此处的acf图中使用了平方数据，而在您的arima教程中却使用了非平方数据？ https://machinelearning.org.cn/arima-for-time-series-forecasting-with-python/
我不知道该用哪一个来确定MA和AR的阶数。

回复
- Jason Brownlee 2020年3月14日上午8:15 #
  
  根据我的经验，最好的方法是网格搜索超参数。
  https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
  
  回复
Tom 2020年3月17日下午12:25 #

嗨，Jason，
我一直听到“方差或波动率随时间变化会给使用ARIMA等经典方法进行时间序列建模带来问题”，因此使用GARCH来解决这个问题。但GARCH似乎只用于预测波动率，那么原始的ARMA模型就没有必要“修复”，我们至少可以对波动率有所了解？那么GARCH的出现是否说明了ARMA时间序列建模的有效性？

回复
- Jason Brownlee 2020年3月17日下午1:39 #
  
  好问题，我在这两种方法结合方面没有好的经验，抱歉。
  
  回复
Dwi 2020年4月10日晚上10:26 #

嗨，Jason，

在您的自相关代码部分，您遗漏了一行代码，您不能直接使用存储在列表中的数据来调用plot_acf。您必须先给它一个形状才能这样做。

举几个例子，您可以使用numpy.array或pandas.DataFrame将其转换。

修复后的代码如下：
import numpy as np squared_data = np.array([x**2 for x in data])

如果我的说法有误，请随时纠正我。

回复
- Jason Brownlee 2020年4月11日上午6:19 #
  
  感谢分享。
  
  回复
Kamlesh Kumar 2020年4月24日凌晨1:11 #

嗨，Jason，

一如既往，这是一篇很棒的文章，我可以毫不犹豫地说，这是我在线找到的最好的机器学习资源之一。我从您的博客中学到了很多东西。

我有一个请求。您能否为零售业务（或任何业务线）做一个需求/销售预测案例研究，其中涵盖了未来1-2年冠状病毒大流行对销售的影响？

谢谢

回复
- Jason Brownlee 2020年4月24日上午5:47 #
  
  谢谢。
  
  很好的建议，谢谢。
  
  回复
Aman Priyaraj 2020年5月17日上午9:58 #

Jason您好，我应该如何绘制训练数据集的GARCH值？实际上我需要表格格式的。

回复
- Jason Brownlee 2020年5月18日上午6:07 #
  
  也许可以将您的数组保存为CSV。
  https://machinelearning.org.cn/how-to-save-a-numpy-array-to-file-for-machine-learning/
  
  回复
William 2020年5月27日下午12:22 #

嗨，Jason，

感谢您的这篇文章。它非常有帮助。

我有一个关于如何在拟合GARCH模型之前处理时间序列中季节性效应的问题。特别是，我试图研究不同变量对价格的影响。然而，因变量和一些自变量都包含季节性。我计划进行一个两阶段的过程，并使用OLS框架（通过添加季节性虚拟变量）分别去除自变量和因变量的季节性。然后拟合ARX-GARCHX模型。这是处理季节性的理想方法吗？

回复
- Jason Brownlee 2020年5月27日下午1:31 #
  
  不客气。
  
  也许可以尝试在拟合/评估模型之前进行季节性差分？
  
  可能存在支持季节性的模型变体，我不太清楚。
  
  回复
William 2020年5月27日下午8:07 #

感谢您的回复，Jason。

是的，我的意思是那样。

回复
- Jason Brownlee 2020年5月28日上午6:13 #
  
  祝你的项目好运！
  
  回复
Ashwal 2020年6月16日凌晨7:31 #

很棒的信息，但我有一个疑问，使用ARCH时我们试图估计波动率(t)，但为什么我们要将其转换为残差项然后进行（残差项的）AR，而不是直接将其转换为方差然后对它们进行ARMA呢？

回复
- Jason Brownlee 2020年6月16日下午1:38 #
  
  如果您愿意，可以直接将AR应用于序列，但您解决的是一个不同的问题，例如预测观测值而不是波动率。
  
  回复
Luigi 2020年7月24日晚上11:22 #

嗨，Jason，
这是一篇很棒的文章。

我有一些问题，

我能否以某种方式将GARCH应用于多变量数据，以考虑不同变量之间的相关性？
例如，假设我想估计欧元/美元汇率的波动率，我在这些数据上应用GARCH并得到波动率的预测。

然而，该指数还将取决于欧元/英镑或英镑/美元汇率的波动率。它们彼此相关，那么我如何进行可以考虑波动率与其他变量相关性的波动率预测？

我听说过动态条件相关法，但找不到很多Python相关的资源。
还有其他建议吗？也许GARCH可以修改以做到这一点？
再次感谢
Luigi

回复
- Jason Brownlee 2020年7月25日上午6:21 #
  
  也许可以，但我没有关于该主题的教程。
  
  回复
Rupesh S 2021年3月24日凌晨2:20 #

1）当我们使用ARCH和GARCH模型时，它们会预测未来值吗？还是只从序列中消除方差和波动率。
2）是否有ARCH和GARCH模型的特定数据集，以及哪种领域会使用这种方法？

回复
- Jason Brownlee 2021年3月24日上午5:52 #
  
  不，它们预测的是预期波动率。
  
  回复
Tarun 2021年4月1日凌晨2:39 #

嗨，Jason，

这确实是关于ARCH和GARCH模型的一个很好的教程。您能否告诉我如何在Python代码中为上述两种模型查找均方根误差（RMSE）、平均绝对误差（MAE）、中位数绝对误差（MedAE）和平均绝对百分比误差（MAPE）？

此致
Tarun

回复
- Jason Brownlee 2021年4月1日上午8:21 #
  
  谢谢。
  
  是的，请看这个
  https://machinelearning.org.cn/regression-metrics-for-machine-learning/
  
  回复
Tarun 2021年4月4日晚上6:45 #

嗨，Jason，

在此教程中，如何找到ARCH模型的阶数？

回复
- Jason Brownlee 2021年4月5日上午6:10 #
  
  您可以使用ACF/PACF图来估计阶数，或者进行阶数网格搜索。
  
  回复
Tarun 2021年4月6日凌晨12:11 #

嗨，Jason，

我已经接近完成ARCH了。正在努力找出ARCH模型的RMSE。请告诉我如何修复它。

代码——

#查找RMSE
from sklearn.metrics import mean_squared_error
np.sqrt(mean_squared_error(test, X_model_forecast))

其中

test = X[240:]

X_model_forecast = X_model_fit.forecast(horizon = 61)

X_model_fit = X_model.fit()

X_model = arch_model(train, mean=’Zero’, vol=’ARCH’, p=15)

错误——

TypeError: Expected sequence or array-like, got

回复
- Jason Brownlee 2021年4月6日上午5:18 #
  
  或许这些提示会有帮助
  https://machinelearning.org.cn/faq/single-faq/can-you-read-review-or-debug-my-code
  
  回复
Tarun Sharma 2021年4月8日晚上10:26 #

嗨，Jason，

对于ARCH模型的参数，我们需要绘制ACF还是PACF？因为在一个关于ARCH的YouTube视频中，有人使用了PACF来做这件事。请澄清。

回复
- Jason Brownlee 2021年4月9日上午5:24 #
  
  可以，而且可能很有帮助。
  
  在实际项目中，我更倾向于快速网格搜索。
  
  回复
Tarun Sharma 2021年4月8日晚上11:05 #

嗨，Jason，

对于ARCH模型，您创建了一个数据集，如下所示：

# 创建数据集
data = [gauss(0, i*0.01) for i in range(0,100)]

如果有人有不同的数据集，比如NASDAQ的收盘指数，而且它不是平稳的，那该怎么办？

请告诉我。

回复
- Jason Brownlee 2021年4月9日上午5:25 #
  
  也许先让您的序列平稳化？
  
  另外，股票价格是不可预测的。
  https://machinelearning.org.cn/ufaqs/can-you-help-me-with-machine-learning-for-finance-or-the-stock-market/
  
  回复
Tarun 2021年4月12日凌晨1:54 #

嗨，Jason，

我有一个问题。您将如何在Python代码中实现GARCH-M和TARCH / GJR-GARCH？

请告知。

回复
- Jason Brownlee 2021年4月12日上午5:10 #
  
  我目前还不清楚，抱歉。
  
  回复
Peyton 2021年4月16日下午2:56 #

嗨，Jason，

感谢这个有用的教程。我想知道您是否知道 Python 中是否有任何用于具有附加协变量的 GARCH 模型的软件包。我希望在 Python 中实现 GARCHX 模型来分析风能和太阳能发电对电力价格波动的影响。

谢谢！

回复
- Jason Brownlee 2021 年 4 月 17 日上午 6:05 #
  
  我当下不知道，抱歉。
  
  回复
Jyothi Manoj 2021 年 6 月 10 日下午 3:13 #

嗨 Jason，很棒的文章。感谢您为让学习变得容易所做的努力。
我有一个疑问。通过将 GARCH 模型与我的 ARIMA 模型结合用于价格预测，我能否提高预测的准确性？

回复
- Jason Brownlee 2021 年 6 月 11 日上午 5:13 #
  
  这取决于您的数据和模型，或许可以开发一个原型并在您的数据上进行评估。
  
  回复
Dario 2022 年 7 月 9 日晚上 11:29 #

你好！

您能向我解释一下预测矩阵的元素吗：特别是均值和方差。
从文档中，我了解到第一个是条件均值，第二个是条件方差。

您能向我展示这两个元素在数学上对应什么吗？或者更好地说，GARCH 过程的公式中有哪一部分是它们？

因为在另一个教程中，我看到可以通过拟合序列上的 ARMA(p,q) 模型和残差上的 GARCH(p,q) 模型来预测平稳序列（在均值上）的未来值，但具有条件异方差性。然后将 ARMA 预测与 GARCH “均值”预测相加。但最后一步对我来说还不清楚。

回复
- James Carmichael 2022 年 7 月 10 日上午 8:45 #
  
  嗨 Dario……以下资源可能很有趣
  
  https://towardsdatascience.com/deep-understanding-of-the-arima-model-d3f0751fc709
  
  回复
Dionysios Kokkoris 2023 年 6 月 22 日晚上 11:08 #

你好，我可以问一下为什么 var = [i*0.01 for i in range(0,100)] 吗？

回复
leo 2023 年 7 月 27 日下午 7:03 #

嗨，Jason，
非常棒的 Python arch 包使用教程。

我对该教程在实际数据中的应用有一些疑问。

如果我有一个值向量，其中我不知道数据的实际均值和方差，我该如何进行？
在您的示例中，您知道每个数据点的方差，并且可以将其与模型预测的值进行比较。如果我期望我的数据中方差发生变化，我该如何将预测与实际值进行比较？

我正在尝试将您的教程改编为期权波动率的预测。

回复
leo 2023 年 7 月 27 日晚上 10:04 #

嗨，做得好。

非常有信息量的博客。继续保持良好的工作。

我有一个进一步的问题
在您的示例中，您知道您的均值和方差，因为您生成了数据。但是，在处理实际数据时，我该如何进行？您能否在示例中扩展真实数据（例如股票价格）来预测波动率？

谢谢

回复
- James Carmichael 2023 年 7 月 28 日上午 9:12 #
  
  Leo，您太客气了！我们感谢您的反馈和建议！确实建议进行探索性数据分析以收集和理解关键特征。
  
  https://machinelearning.org.cn/understand-problem-get-better-results-using-exploratory-data-analysis/
  
  回复

导航

如何在 Python 中使用 ARCH 和 GARCH 模型为时间序列预测建模波动性

教程概述

方差问题

什么是 ARCH 模型？

什么是 GARCH 模型？

如何配置 ARCH 和 GARCH 模型

Python 中的 ARCH 和 GARCH 模型

测试数据集

自相关

ARCH 模型

GARCH 模型

进一步阅读

论文和书籍

API

文章

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入
您自己的项目

关于此主题的更多信息

95 条回复关于“如何在 Python 中为时间序列预测开发 ARCH 和 GARCH 模型”

留下回复点击此处取消回复。

导航

教程概述

方差问题

什么是 ARCH 模型？

什么是 GARCH 模型？

如何配置 ARCH 和 GARCH 模型

Python 中的 ARCH 和 GARCH 模型

测试数据集

自相关

ARCH 模型

GARCH 模型

进一步阅读

论文和书籍

API

文章

总结

想用Python开发时间序列预测吗？

几分钟内开发您自己的预测

最终将时间序列预测带入您自己的项目

关于此主题的更多信息

95 条回复关于“如何在 Python 中为时间序列预测开发 ARCH 和 GARCH 模型”

留下回复 点击此处取消回复。

最终将时间序列预测带入
您自己的项目

留下回复点击此处取消回复。