积分微积分是牛顿和莱布尼茨最伟大的发现之一。他们的工作独立地导出了微积分基本定理的证明和其重要性的认可,该定理将积分与导数联系起来。随着积分的发现,面积和体积从此可以被研究。
积分微积分是我们探索的微积分旅程的第二部分。
在本教程中,您将发现微分微积分和积分微鉴之间的关系。
完成本教程后,您将了解:
- 微分微积分和积分微鉴的概念通过微积分基本定理联系在一起。
- 通过应用微积分基本定理,我们可以计算积分来找到曲线下的面积。
- 在机器学习中,积分微鉴的应用可以为我们提供一个评估分类器性能的度量。
让我们开始吧。

微分和积分微积分 – 对任何事物进行微分
照片由Maxime Lebrun拍摄,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 微分和积分微鉴 – 它们之间的联系是什么?
- 微积分基本定理
- 扫掠面积类比
- 微积分基本定理 – 第一部分
- 微积分基本定理 – 第二部分
- 积分示例
- 积分在机器学习中的应用
微分和积分微鉴 – 它们之间的联系是什么?
在我们迄今为止的微积分旅程中,我们已经了解到微分微鉴关注的是变化率的测量。我们还发现了微分,并从第一原理中将其应用于不同的函数。我们甚至理解了如何应用规则来更快地得到导数。
但我们只走了一半的路程。
从二十一世纪的视角来看,微积分通常被视为变化的数学。它使用两个主要概念来量化变化:导数和积分。导数模拟变化率……积分模拟变化的累积……
– 第 141 页,Infinite Powers, 2020。
回顾我们说过微积分包含两个阶段:切割和重建。
切割阶段将一个曲线形状分解成无穷小的直线片段,这些片段可以单独研究,例如通过应用导数来模拟它们的变化率,或称为*斜率*。
微积分旅程的这个阶段称为*微分微鉴*,我们已经详细研究过它。
重建阶段收集无穷小的直线片段,并将它们重新组合起来,试图研究原始整体。通过这种方式,在将规则形状和不规则形状切成无穷薄的切片后,我们可以确定它们的面积或体积。微积分旅程的第二部分是我们接下来将要探索的。它被称为*积分微鉴*。
连接这两个概念的重要定理称为*微积分基本定理*。
微积分基本定理
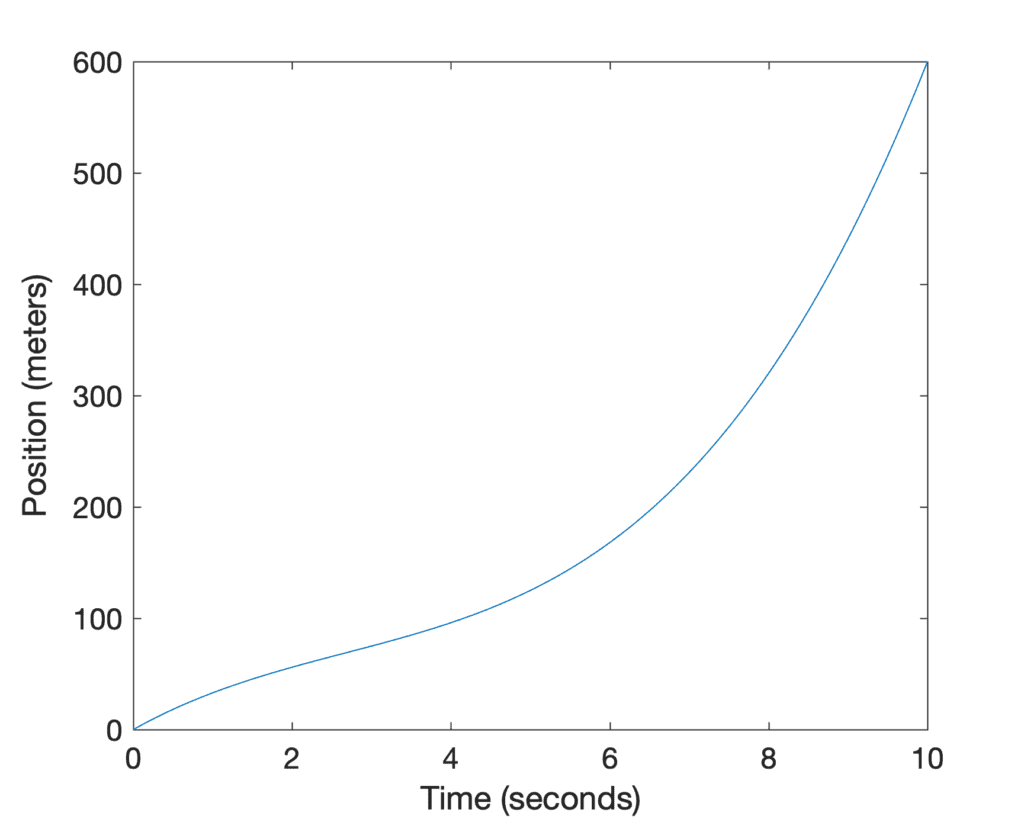
为了更好地理解微积分基本定理,让我们回顾一下汽车的位置和速度示例:
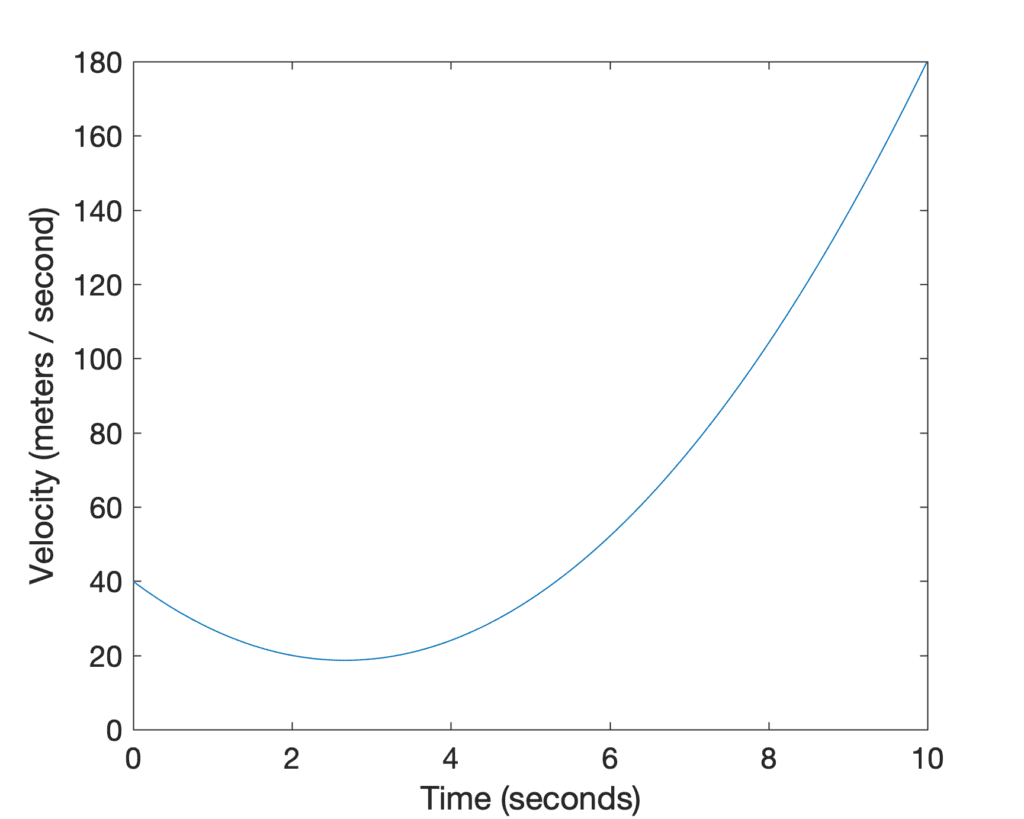
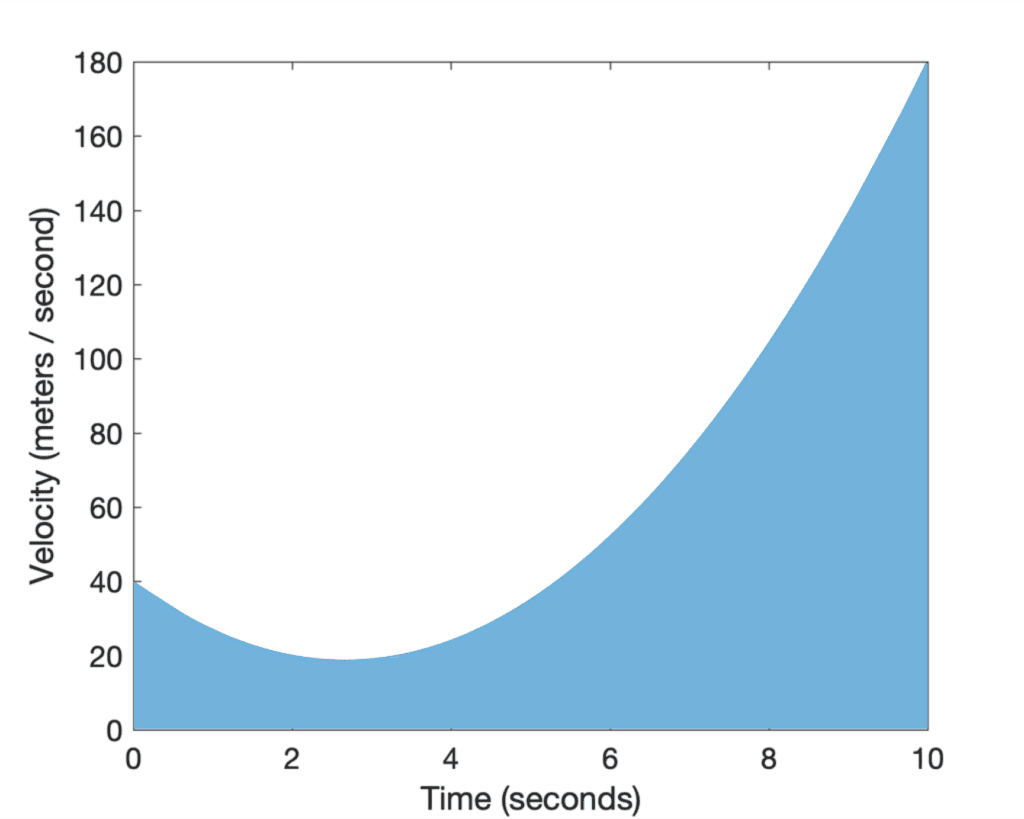
在计算导数时,我们解决了*正向*问题,即在任何时间点 *t*,我们都从位置图的斜率中找到了速度。但是,如果我们想解决*反向*问题,即已知速度图 *v*(t),并希望找到行驶的距离呢?这个问题的解决方案是计算直到时间 *t* 的*曲线下的面积*(阴影区域)
我们没有具体的公式可以直接定义阴影区域的面积。但是我们可以应用微积分的数学,将曲线下的阴影区域切成许多无穷薄的矩形,我们有计算它们面积的公式。
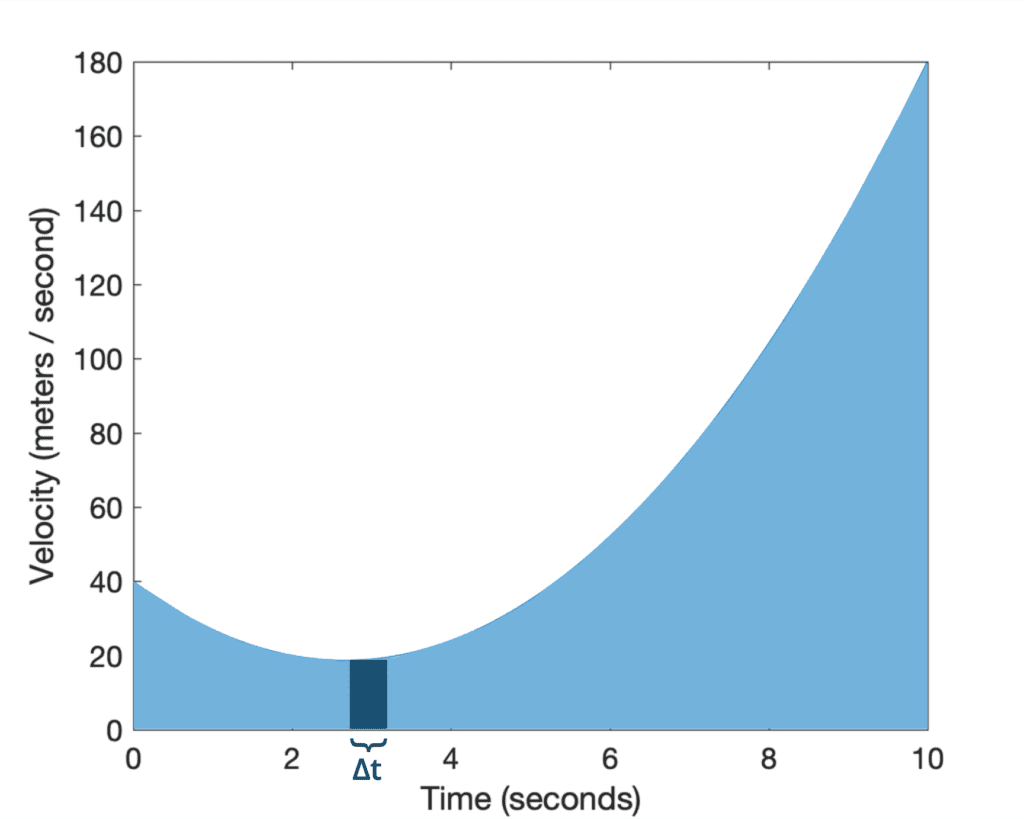
如果我们考虑第 *i* 个矩形,任意选择其跨越时间间隔 Δt,我们可以将其面积定义为其长度乘以宽度
矩形面积 = *v*(ti) Δti
我们可以使用任意多的矩形来覆盖感兴趣的区间,在本例中是曲线下的阴影区域。为简单起见,我们将此闭区间表示为 [a, b]。找到该阴影区域的面积(从而确定行驶的距离),就归结为找到 *n* 个矩形的总和
总面积 = *v*(t0) Δt0 + *v*(t1) Δt1 + … + *v*(tn) Δtn
通过应用黎曼和与西格玛符号,我们可以更紧凑地表达这个和
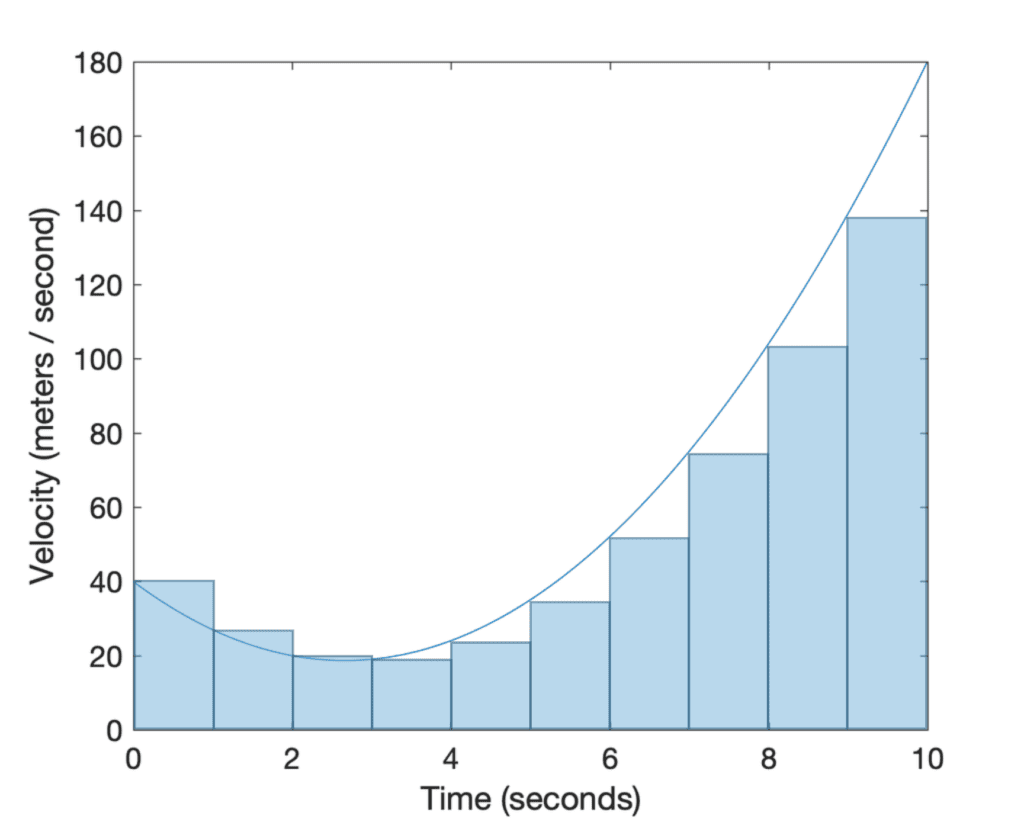
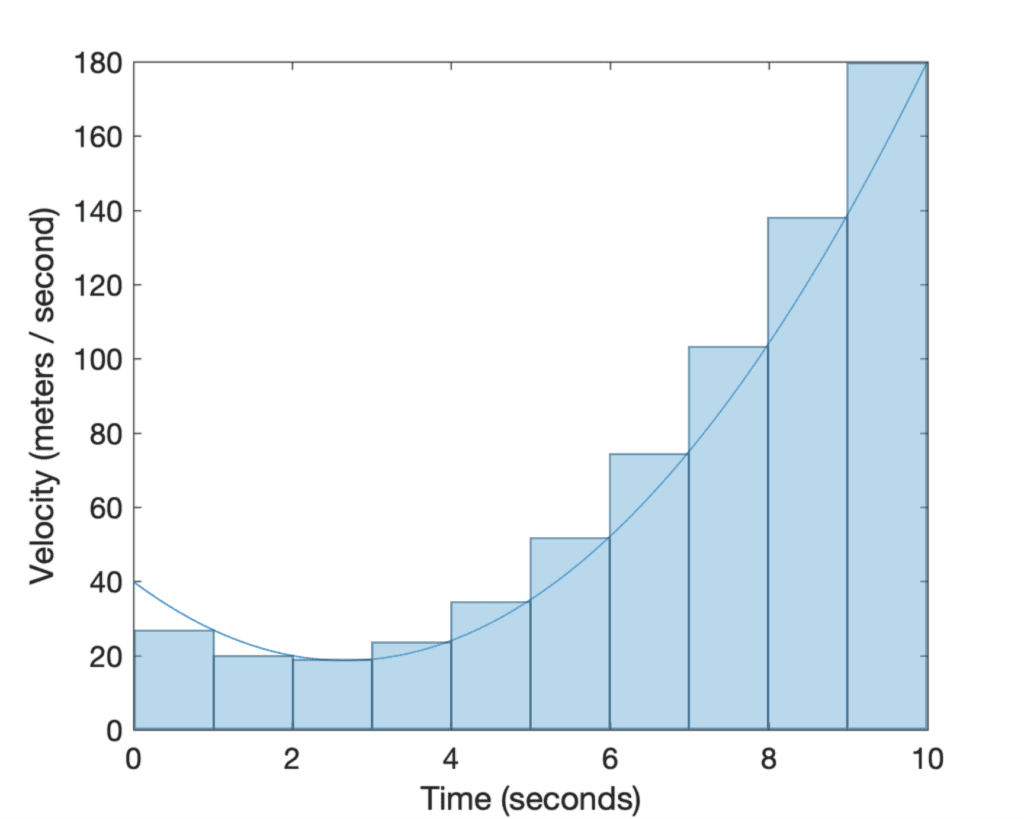
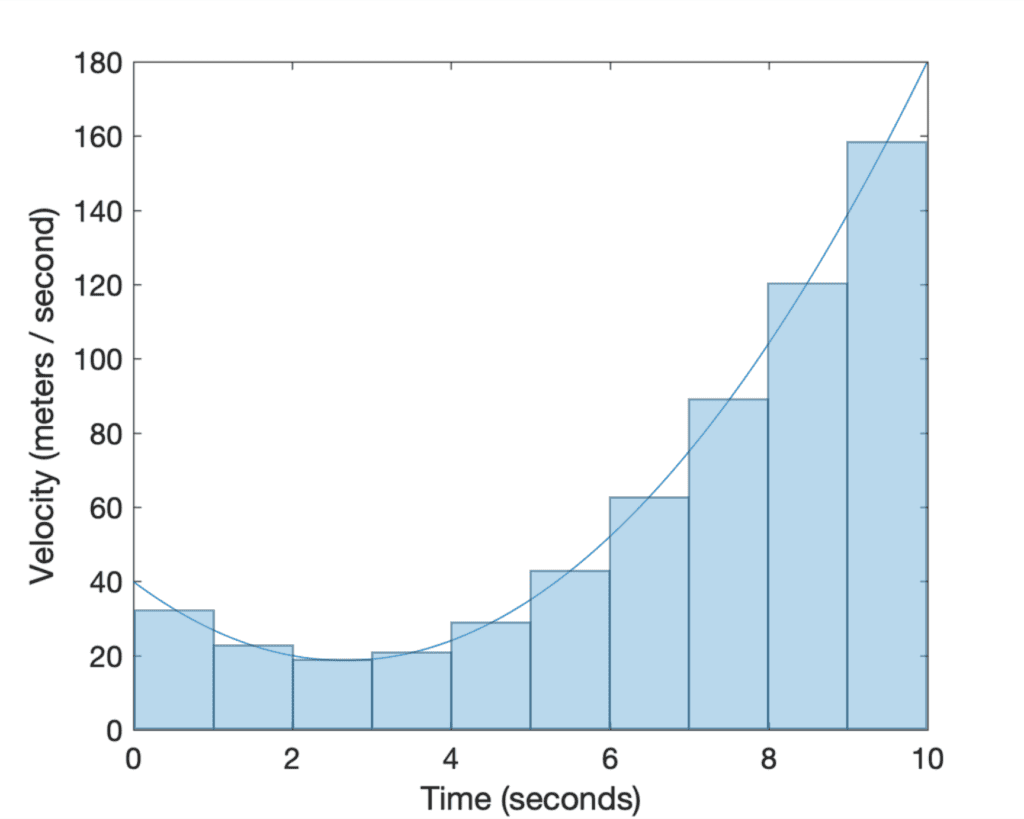
如果我们用有限数量的矩形切割(或分割)曲线下的区域,我们就会发现黎曼和给出了面积的*近似值*,因为矩形不能完全贴合曲线下的区域。如果我们选择矩形的左上角或右上角接触曲线,黎曼和分别给出实际面积的低估或高估。如果每个矩形的中点接触曲线,那么超出曲线的矩形部分*大致*会补偿曲线与相邻矩形之间的差距。
找到曲线下*精确*面积的解决方案是,将矩形的宽度缩小到*无限薄*(回顾微积分中的无穷原理)。这样,矩形就会覆盖整个区域,通过将它们的面积相加,我们就能找到*定积分*。
定积分(“简单”定义):在 t = a 和 t = b 之间曲线下的精确面积由定积分给出,定积分定义为黎曼和的极限……
– 第 227 页,Calculus for Dummies, 2016。
当矩形数量 *n* 趋近于无穷大时,定积分可以通过黎曼和定义。我们也将曲线下的面积表示为 *A*(*t*)。那么
请注意,符号现在变为积分符号 ∫,取代了西格玛符号 Σ。这样改变的原因仅仅是为了表明我们正在对大量薄切片的矩形进行求和。左侧的表达式读作“v(*t*) 从 a 到 b 的积分”,而寻找积分的过程称为*积分*。
扫掠面积类比
也许有一个更简单的类比可以帮助我们理解积分与微分的关系,想象一下拿起一个薄切片,并在曲线下以无穷小的步长向右拖动它。当它向右移动时,这个薄切片将在曲线下扫过更大的面积,同时其高度会根据曲线的形状而变化。我们想回答的问题是,当薄切片向右扫掠时,面积累积的*速率*是多少?
设 *dt* 表示扫掠切片遍历的每个无穷小步长,*v*(*t*) 表示其在任何时间 *t* 的高度。那么,该薄切片的无穷小面积 *dA*(*t*) 可以通过将其高度 *v*(*t*) 乘以其无穷小宽度 *dt* 来找到
*dA*(*t*) = *v*(*t*) *dt*
将等式除以 *dt*,我们得到 *A*(*t*) 的导数,并告诉我们面积累积的速率等于曲线的高度 *v*(*t*) 在时间 *t*。
*dA*(*t*) / *dt* = *v*(*t*)
我们终于可以定义微积分基本定理了。
微积分基本定理 – 第一部分
我们发现,函数 *v*(*t*) 下扫过的面积 *A*(*t*) 可以定义为
我们还发现,面积被扫过的速率等于原始函数 *v*(*t*)
*dA*(*t*) / *dt* = *v*(*t*)
这就引出了微积分基本定理的第一部分,它告诉我们,如果 *v*(*t*) 在区间 [a, b] 上是连续的,并且它也是 *A*(*t*) 的导数,那么 *A*(*t*) 就是 *v*(*t*) 的*反导数*。
*A’*(*t*) = *v*(*t*)
或者更简单地说,积分是微分的逆运算。因此,如果我们先积分 *v*(*t*),然后再对结果进行微分,我们就会得到原始函数 *v*(*t*)。
微积分基本定理 – 第二部分
该定理的第二部分为我们提供了一种计算积分的捷径,而无需采用计算黎曼和极限的较长路径。
它规定,如果函数 *v*(*t*) 在区间 [a, b] 上是连续的,那么
这里,*F*(*t*) 是 *v*(*t*) 的任何反导数,积分被定义为在 b 和 a 处求值后的反导数之差。
因此,该定理的第二部分通过将某些起始点 *C* 和下限 *a* 之间的曲线下的面积,减去相同起始点 *C* 和上限 *b* 之间的面积,来计算积分。这有效地计算了 *a* 和 *b* 之间的感兴趣区域。
由于常数 *C* 定义了扫描开始的 x 轴上的点,因此最简单的反导数是 *C* = 0 的情况。尽管如此,也可以使用任何 *C* 值的反导数,它只是将起始点设置在 x 轴上的不同位置。
积分示例
考虑函数 *v*(*t*) = x³。通过应用幂法则,我们可以轻松找到其导数 *v’*(*t*) = 3x²。3x² 的反导数再次是 x³ – 我们执行逆运算来得到原始函数。
现在假设我们有一个不同的函数 *g*(*t*) = x³ + 2。它的导数也是 3x²,另一个函数 *h*(*t*) = x³ – 5 的导数也是如此。这些函数(以及其他类似的函数)都有 x³ 作为它们的反导数。因此,我们通过*不定积分*来指定 3x² 的所有反导数的族。
不定积分没有定义计算曲线下面积的区间。常数 *C* 被包含进来,以补偿关于区间或扫描起始点的信息缺失。
如果我们确实知道这些区间,那么我们就可以应用微积分基本定理的第二部分来计算*定积分*。
在这种情况下,我们只需将 *C* 设置为零,因为它不会改变结果。
积分在机器学习中的应用
我们已经将汽车的速度曲线 *v*(*t*) 作为一个熟悉的例子来理解积分和微分之间的关系。
但是,您可以使用这种将矩形面积相加的方案来累加任何微小的部分——例如距离、体积或能量。换句话说,曲线下的面积不一定代表实际的面积。
– 第 214 页,Calculus for Dummies, 2016。
成功应用机器学习技术的一个重要步骤是选择适当的性能指标。例如,在深度学习中,通常的做法是衡量*精确率*和*召回率*。
*精确率是模型报告的检测中正确的比例,而召回率是被检测到的真实事件的比例。*
– 第 423 页,Deep Learning, 2017。
通常还会将精确率和召回率绘制在精确率-召回率(PR)曲线图上,将召回率放在 x 轴,精确率放在 y 轴。理想情况下,一个分类器应该同时具有高召回率和高精确率,这意味着分类器能够正确地检测到许多真实事件。这种良好的分类性能将由 PR 曲线下的较高面积来表征。
您可能已经猜到接下来会讲什么了。
PR 曲线下的面积可以通过应用积分微鉴来计算,这使我们能够表征分类器的性能。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 单变量和多变量微积分, 2020.
- 微积分傻瓜书, 2016.
- 无限力量, 2020.
- 微积分搭便车指南, 2019.
- 深度学习, 2017.
总结
在本教程中,您发现了微分微鉴与积分微鉴之间的关系。
具体来说,你学到了:
- 微分微积分和积分微鉴的概念通过微积分基本定理联系在一起。
- 通过应用微积分基本定理,我们可以计算积分来找到曲线下的面积。
- 在机器学习中,积分微鉴的应用可以为我们提供一个评估分类器性能的度量。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。
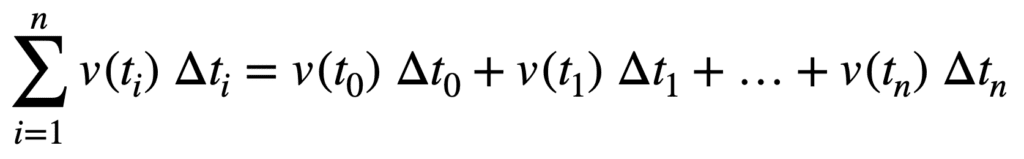
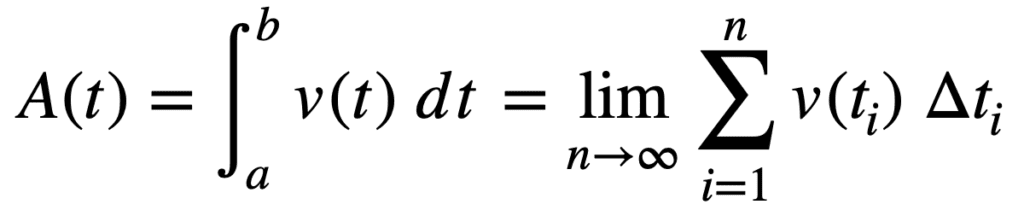
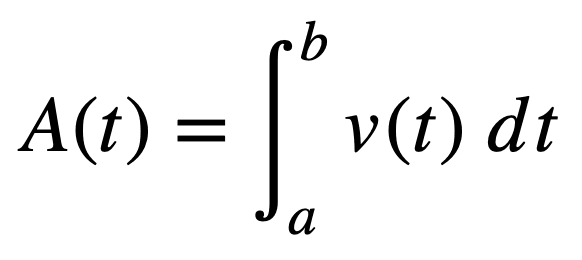
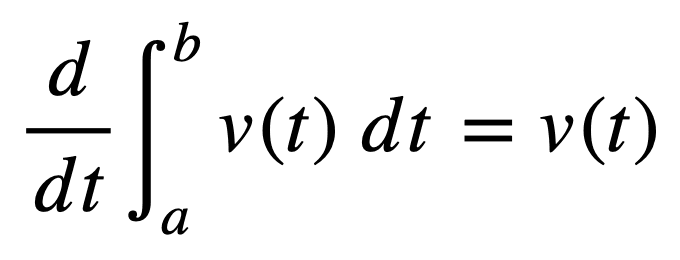
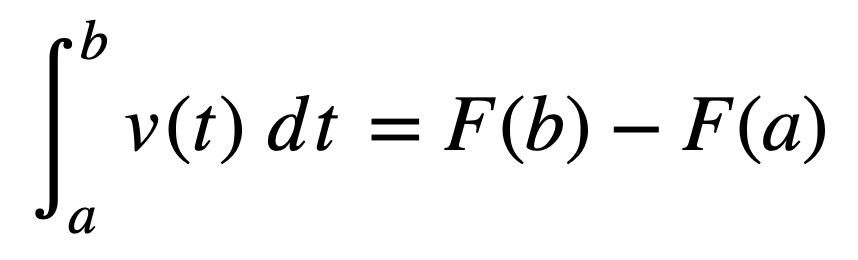
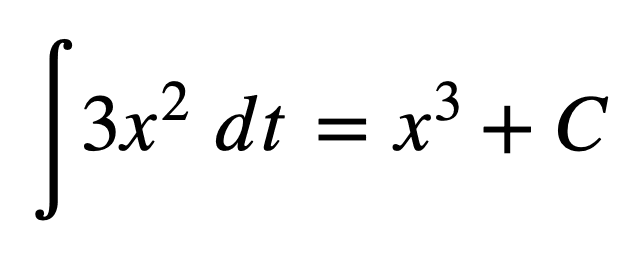
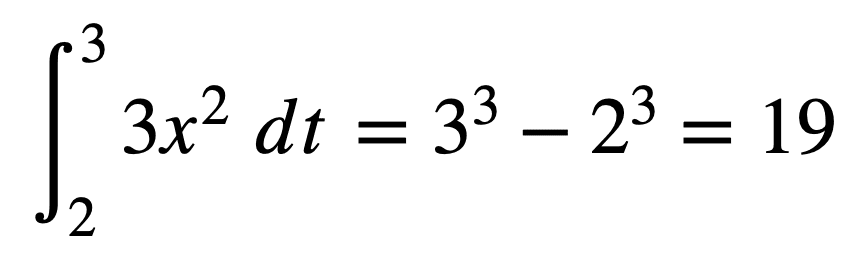






感谢您提供关于微分和积分计算的宝贵信息以及清晰易懂的示例。
用示例很好地展示了这个主题
感谢您的支持和反馈 Sushant!
你好!